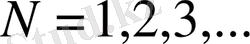Беллманның оңтайлылық принципі және динамикалық бағдарламалау әдістері


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 22 бет
Таңдаулыға:
Қазақстан Республикасының Білім және Ғылым министрлігі
КУРСТЫҚ ЖҰМЫС
Тақырыбы:
«Беллманның оңтайлау принципі. Динамикалық программалау есебін шешудің әдісі»
Орындаған:
Тексерген:
Орал, 2013ж.
Мазмұны
Кіріспе . . . 3
1. Математикалық модельдеу туралы жалпы түсінік
1. 1. Математикалық модельдер және түрлері . . . 5
1. 2. Динамикалық программалау туралы түсінік . . . 9
2. Динамикалық программалау есебі және Беллманның оңтайлау принципі
2. 1. Динамикалық программалау есебінің қойылуы . . . 11
2. 2. Р. Беллманның оңтайлау принципін пайдаланып есеп шығару . . . 16
Қорытынды . . . 25
Пайдаланылған әдебиеттер тізімі . . . 27
Кіріспе
« Математикалық модельдеу» пәнін оқытудағы мақсат сызықтық және сызықтық емес бағдарлама есептерінің модельдерін құру, олардың максимум және минимум мәндерін табу, екіжақты, транспорттық, вариациалау және ойын теориясының есептерін шешіп, математикалық статистика элементтерімен танысып, көпшілікке қызмет ету жүйесінің модельдерін шешуге үйрену болып табылады.
Модельдер теориясының негізгі есебі - ол теориялардың жəне олардың модельдер кластарының екі негізгі ұғымның классификациясын өткізу. Бекітілген теориялардың модельдері əр түрлі əдістермен өзара классификацияланады, мысалы, изоморфизм, элементарлы эквиваленттік.
Динамикалық бағдарламалау математика, компьютер ғылымы, және экономика ғылымдарында күрделі есепті қарапайым кіші есептерге бөлу арқылы шығарылатын метод. Динамикалық бағдарламалау əр алуан экстремалды есептерді шешудің сандық тəсілдерін талдаумен жəне жасаумен айналысатын қолданбалы математиканың жаңа тарауы екендігі көрсетілген.
Экономикалық үдерістерді жеке қадамдарға бөліп көрсету күрделі есептерді едəуір оңайлатуға мүмкіндік беретіндігі дəлелденген. Динамикалық бағдарламалау есептері Ричард Беллманның оңтайлылық принципін дəл бейнелейтін функционалды теңдеулерді қолдануға болатындығы көрсетілген. Кен өнеркəсібінде ресурстарды оңтайлы бөлу есептерін шешу үшін динамикалық бағдарламалауды қолдану мүмкіндігі ашылған. Динамикалық бағдарламалау тəсілдерімен көмір өндіру кəсіпорындары арасында күрделі қаржыны оңтайлы бөлу есебін шешу алгоритмі ұсынылған.
Математикалық модельдеу үрдісінің негізгі бөлігі аппроксимация (жуықтау) - математикалық амалдарды (функция, теңдеу т. с. с. ) басқа қарапайым шамалар арқылы жуықтап табу болып табылады. Аппроксимацияның көмегімен күрделі есептерді жай есептерге, сызықтық емес теңдеулерді сызықтық теңдеулерге келтіреді.
Динамикалық бағдарламалау - оптималды бағдарламалау есептерінің бір тарауы, көп сатылы, көп адымды есептердің оптималды шешімін табатын әдіс. Бұл әдіс уақыты көрсетілмеген есептерде де қолданылады. Яғни динамика шығарылатын есептерде емес оның шығарылу әдістерінде.
Курстық жұмыстың мақсаты: динамикалық программалау есебі Ричард Беллманның оңтайлылық принципімен танысу.
Курстық жұмыстың міндеттері: Математикалық модельдер ұғымына түсінік беру және динамикалық бағдарламалау әдісін қолдану арқылы есептер шығару, динамикалық бағдарламалауға түсінік беру. Ричард Беллманның оңтайлылық принципіне түсінік беру.
Курстық жұмыстың құрылымы: кіріспеден, екі бөлімнен және қорытынды мен әдебиеттер тізімінен тұрады.
1. Математикалық модельдеу туралы жалпы түсінік
1. 1. Математикалық модельдер және түрлері
Математикалық модельдермен зерттелетін объекті мен үрдістің қасиеттері, ерекшеліктері және сипаттамалары теңдеулер жүйелері, теңсіздіктер және функция арқылы көрсетіледі.
Көптеген математикалық модельдер универсалды болып келеді, яғни әртүрлі жүйелерді зерттеуге қолданылады. Математикалық модельдер қарастырылатын құбылыстар мен үрдістердің сандық заңдылықтарын анықтауға, сипатталатын факторлардың тәуелділігі мен өзара байланысын табуға мүмкіндік береді. Математикалық модельдердің дамуына өте күрделі есептеулерді жүргізетін электронды-есептегіш машиналарының көбеюі зор ықпал етті.
Көптеген математикалық модельдер параметрлер мен айнымалылардан тұратын теңдеулер мен теңсіздіктер жүйелерінен тұрады. Айнымалы шамалар, мысалы, өндірілген өнім көлемі, капитал жұмсау, тасымалдау т. с. с., ал параметрлер өнімді өндіруге жұмсалған материал, уақыт, шикізат шығынының мөлшерін көрсетеді. Әрбір модельде айнымалылардың екі тобын көрсетуге болады.
1) Сыртқы айнымалылар - олардың мәндері модельден тыс және берілген;
2) Ішкі айнымалылар, олардың мәндері берілген модельді зерттеу қорытындысында анықталады.
Модельдеу үрдісінің нақты алгоритмі жоқ, бірақ модельдеу тәжірибесінде басшылықққа алатын анықталған принциптер бар.
Құрылымдық модельді оқып үйрену үстінде объектінің мазмұнын туралы, оның сыртқы жағдайларға әсері туралы информацияларды алуға болады. Ал функционалдық модельді зерттегенде объектінің әртүрлі реакцияларының сыртқы ортаға әсері туралы деректер алуға болады. Сонымен қатар объектінің құрылымын талдауға және құрылымдық модельдерді құруға мүмкіндіктер туады.
Экономикалық-математикалық модельдер жүйе жағдайын болашақты жоспарлау мен болжауға пайдаланады. Мұндай жағдайда модель оның негізінде қойылған белгілі бір алғы шарттарға сәйкес экономикалық үрдістердің ағымын көрсетеді. Жоспарлау мен болжау модельдерінде алғышарттарды дұрыс таңдау ерекше маңызды роль атқарады. Модель есептің шарты дұрыс қойылған кезде ғана нақты жүйелердің құрылысы мен функциясын дұрыс сипатайды.
Экономикалық-математикалық модельдер сипаттаулы және оптималды болып бөлінеді.
Экономикалық жүйелердің сипаттаулы моделі есептерді математикалық формула түрінде көрсетеді және жүйе жағдайы мен оның элементтерінің байланысын тереңірек ұғып үйренуге қолданылады.
Математикалық модельдерде сызықтық және сызықтық емес тәуелділіктердің әртүрлі түрлері қолданылады.
Математикалық модельдеу үрдісінің негізгі бөлігі аппроксимация (жуықтау) - математикалық амалдарды (функция, теңдеу т. с. с. ) басқа қарапайым шамалар арқылы жуықтап табу болып табылады. Аппроксимацияның көмегімен күрделі есептерді жай есептерге, сызықтық емес теңдеулерді сызықтық теңдеулерге келтіреді.
Модельденетін обьектінің белгілі бір уақытқа немесе уақыт аралығына сәйкес қасиеттерін сипаттайтын математикалық модельдер статикалық деп аталады.
Үрдістердің белгілі бір уақыт аралығындағы өзгерістерін зерттейтін модельдер динамикалық деп аталады.
Детерминистикалық (латынша determino - анықтау) модельдер дегеніміз барлық параметрлері және сыртқы айнымалылары бірге тең ықтималдықпен анықталатын модельдер.
Ықтималдық модельдерінде параметрлер мен сыртқы айнымалылар немесе олардың белгілі бір бөлігі тиісті ықтималдықтың үлестіруімен сипатталады.
Анықталмағандықты есепке алатын модельдерге ықтималдық теориясының заңдарын қолдануға болмайды.
Математикалық модель жасау процесі өзара байланысқан бірнеше кезеңнен тұрады.
Бірінші кезең - есептің қойылуы. Бұл кезең зерттеудің мақсатын анықтаудан басталады.
Мысалы, кәсіпорын үшін өнім өндіру немесе жүк тасымалдаудың оптималды жоспарын құру немесе берілген материалды кесіп-пішудің оптималды нұсқасын табу қажет т. с. с. Зерттеудің мақсатына сәйкес жүйелерді жан-жақты талдап, оның құрылымы мен қызметін, ерекшелктерін ескеру керек.
Жүйелерді модельдеген кезде модельге есептің шешіміне әсер ететін, яғни қойылған мақсатқа қол жеткізетін факторлардың енуі шарт.
Екінші кезең - таңдалып алынған жүйелерге математикалық модельдер құру. Бұл кезеңде есепті формула түріне келтіру - математикалық тәуелділіктерді теңдеулер, теңсіздіктер түрінде құру жүргізіледі.
Алдағы уақытта есептердің математикалық формула түрінде жазылған өрнектерін есептің моделі деп атаймыз.
Үшінші кезең - құрылған модельге сәйкес есептің шешімін алу.
Бұл кезеңнің негізгі есептерін қарастырайық. Біріншіден, модельге қажетті алғашқы ақпараттарды жинау, параметрлер мен сыртқы айнымалылардың сандық мәндерін анықтау қажет. Екіншіден, есептің шешімін алатын әдісті таңдап алу керек. Сандық экономикалық-математикалық әдістердің арасында кеңінен тарағандары симплекс әдісі және потенциал әдісі. Олар көптеген экономикалық есептерді шығаруға қолданылады. Бұл әдістермен шығаруға келмейтін есептер де кездеседі. Мұндай жағдайларда жүйелерді зерттеудің эвристикалық және имитациялық әдістері қолданылады.
Эвристика (грек сөзінен - табамын, ойлап табамын, ашамын) - зерттеушінің интуициясы мен жүргізген тәжірибесіне сәйкес шешілетін әдістердің жиынтығы. Имитация - модельдеудің мүмкіндігін кеңейтетін жаңа бағыт болып табылады. Имитациялық модельдеуді нақты жүйелердің модельдеріне жүргізілген эксперимент ретінде түсінуге болады, ал жеке алғанда математикалық модельдеудің көмегімен алғашқы шарттарын өзгерте отырып жүргізілетін есептеу эксперименті.
Имитация (латынша - еліктеу) - жасанды құралдардың көмегімен бір нәрсені жаңадан ендіру немесе еске түсіру.
Төртінші кезең - модель бойынша алынған қорытындыны тәжірибеде қолдану. Математикалық әдістердің көмегімен алынған шешімдер талданып, белгілі бір аралықта алғашқы ақпараттарға тигізетін әсері тексеріледі.
Уақыттың өзгеруіне сәйкес алғашқы ақпараттар өзгереді, сол өзгерістердің алынатын шешімдерге тигізетін әсерін білу аса маңызды.
1. 2
.
Динамикалық программалау туралы түсінік
Сызықтық және бейсызықтық бағдарламалау есептерінде экономика-лық үдеріс статикалық, яғни уақыттан тәуелсіз деп қарастырылатындықтан, тиімді шешімі жоспарлаудың бір ғана кезеңіне анықталатын. Бұндай есептер бір кезеңдік немесе бір қадамдық делінеді.
Динамикалық бағдарламалау есептерінде экономикалық үдеріс уақыттан тәуелді, бірнеше уақыт кезеңінен тұратындықтан әрбір кезеңдерінің тиімді шешімдері анықталады, осы негізде бүкіл үдерістің тиімді ұласуы қалыптасады. Осы себепті динамикалық бағдарламалау есептері көп кезеңді немесе көп қадамды деп аталады.
Экономикалық үдеріс басқарылымды делінеді, егер оның дамуына әсер ету мүмкін болса. Әрбір кезеңде үдеріс барысына әсер ететін шешімдер жиынтығы басқару деп аталады.
Көп кезеңді үдерісті жоспарлағанда, тұтас үдерістің талаптарынан шығатындай етіп, жеке кезеңдегі шешімдер қабылданады.
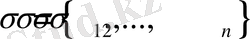 жүйесінің
жүйесінің
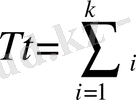 уақытындағы қызметі жоспарлансын, мұндағы
уақытындағы қызметі жоспарлансын, мұндағы
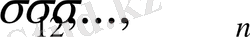 - кәсіпорындары,
- кәсіпорындары,
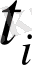 - әрбір кезең (шаруашылық жылы) . Т периодының басталуында бөлінген негізгі қаржы
- әрбір кезең (шаруашылық жылы) . Т периодының басталуында бөлінген негізгі қаржы
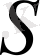 , жүйенің бастапқы жағдайы
, жүйенің бастапқы жағдайы
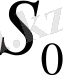 , соңғы жағдайы
, соңғы жағдайы
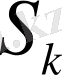 . Т периодының ақырында кәсіпорындар жүйесінің қосынды кірісі
. Т периодының ақырында кәсіпорындар жүйесінің қосынды кірісі
 максималды болатындай етіп, негізгі қаржы
максималды болатындай етіп, негізгі қаржы
 кәсіпорындарына әрбір кезеңге қалай бөлінеді?
кәсіпорындарына әрбір кезеңге қалай бөлінеді?
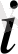 -шы жыл басында
-шы жыл басында
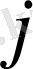 -ші кәсіпорынға
-ші кәсіпорынға
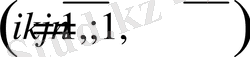 бөлінетін қаржы
бөлінетін қаржы
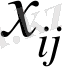 десек, басқару
десек, басқару
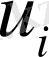 анықталады, яғни
анықталады, яғни
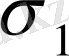 кәсіпорнына
кәсіпорнына
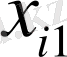 ,
,
 кәсіпорнына
кәсіпорнына
 , . . . ,
, . . . ,
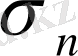 кәсіпорнына
кәсіпорнына
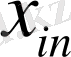 үлестері бөлініп,
үлестері бөлініп,
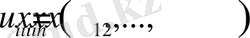 басқару векторы анықталады.
басқару векторы анықталады.
Бөлінген қаржылар жиынтығы k қадамдарында n-өлшемді кеңістіктің келесі векторлар жүйесімен анықталады


. . .

Сонымен k жылдарындағы қосынды кіріс басқарулар жиынтығынан тәуелді, яғни
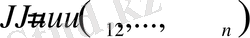
Онда есеп былай қойылады: әрбір кезеңдегі басқаруды, кәсіпорындар жүйесінің қосынды кірісі максималды болатындай етіп таңдау қажет.
Математикалық моделі
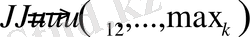
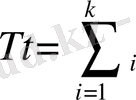 ;
;
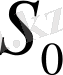 ,
,
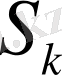 ;
;
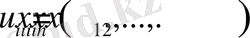
2. Динамикалық программалау есебі және Беллманның
оңтайлау принципі
2. 1. Динамикалық программалау есебінің қойылуы
Математикалық бағдарламалау есептерінің кез келгенінде айнымалыларға қойылған шектеулерге сәйкес мақсатты функцияның экстремумын табу қажет.
Осыған дейін мақсатты функция мен шектеулері сызықтық болып келген есептер қарастырылды. Ал нақты есептерде сызықтық емес тәуелділіктер көптеп кездесетіндіктен сызықтық емес бағдарламалау теориясының жасалу қажеттігі туды.
Қазіргі кезде сызықтық емес бағдарламалау есептері жылдам дамып келеді. Математикалық бағдарламалау есептерінің мақсатты функциясы мен шектеулері сызықтық емес болса, онда ондай есептер сызықтық емес бағдарламалау есептері деп аталады.
Басқарылатын физикалық жүйе
 бастапқы
бастапқы
 жағдайынан уақыт өте келе ақырғы
жағдайынан уақыт өте келе ақырғы
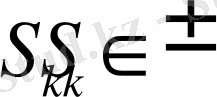 жағдайына келтіріледі. Жағдайлардың өзгеріс үдерісімен сандық белгі
жағдайына келтіріледі. Жағдайлардың өзгеріс үдерісімен сандық белгі
 байланысты. Үдерісті осы сандық белгі тиімді (оптималды) мәнін қабылдайтындай етіп ұйымдастыру қажет.
байланысты. Үдерісті осы сандық белгі тиімді (оптималды) мәнін қабылдайтындай етіп ұйымдастыру қажет.
Мүмкін болатын басқарулар жиынын
 деп белгілейміз. Онда есеп былай қойылады:
деп белгілейміз. Онда есеп былай қойылады:
 жүйесін бастапқы
жүйесін бастапқы
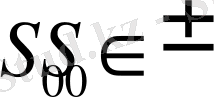 жағдайынан, ақырғы
жағдайынан, ақырғы
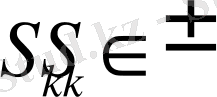 жағдайына белгі
жағдайына белгі
 тиімді
тиімді
 мәнін қабылдайтындай етіп келтіретін,
мәнін қабылдайтындай етіп келтіретін,
 басқаруын анықтау керек.
басқаруын анықтау керек.
Математикалық түрде
 ,
,
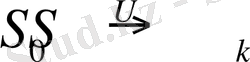 ,
,
 ,
,
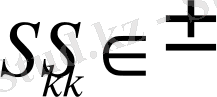 .
.
Динамикалық бағдарламалау көп қадамды үдерісті кезеңдермен жоспарлайтындықтан, үдерістің тұтас дамуын ескере отырып, әрбір қадамын келешекті ескере отырып тиімді етеді.
Әрбір үдерістің соңғы k-ші қадамы бар, онда шешімді қабылдау келешектен тәуелсіз. Осы себепті бұл қадамда ең үлкен әсер басқару қабылданады. Бұл қадамды жоспарлап алып, оның алдынғы (k-1) -қадам тіркеледі, ал оған өз кезегінде (k-2) -қадам тіркеледі т. с. с. Ақырында бастапқы
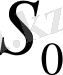 жағдайына келеді. Динамикалық бағдарламалау осылайша ақырынан бастапқы жағдайға оралатындай болып түзіледі.
жағдайына келеді. Динамикалық бағдарламалау осылайша ақырынан бастапқы жағдайға оралатындай болып түзіледі.
k-ші қадамды жоспарлау үшін жүйенің (k-1) -ші қадамындағы жағдайын білу керек. Егер жүйенің (k-1) -ші қадамындағы жағдайы белгісіз болса, үдерістің сипатында, осы қадамдағы жағдайына мүмкін болатындай әр түрлі болжамдар жасалады. Соңғы k-ші қадамда әрбір болжамға тиісті тиімді басқару анықталады. Мұндай тиімді басқару шартты тиімді делінеді.
k қадамды үдеріс жоспарланады. Жүйенің (k-1) -ші қадамдағы мүмкін болатын жағдайларды
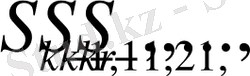 делік. Соңғы қадамда олардың әрқайсысына шартты тиімді басқаруларын
делік. Соңғы қадамда олардың әрқайсысына шартты тиімді басқаруларын

табамыз. Осылайша k-ші қадамы жоспарланады. Шындығында, соңғы қадам алдында жүйе қандай жағдайда болмасын, алдын ала белгілі соңғы қадамда қандай басқару қабылданатыны. Дәл осылайша (k-1) -ші қадамда да шартты тиімді қадам басқаруы k-ші қадамдағы шартты тиімді қортындыда жүйенің бастапқы
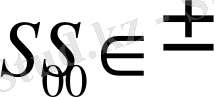 жағдайына келеміз.
жағдайына келеміз.
Басқа қадамдарға қарағанда жүйенің бірінші қадамда мүмкін болатын жағдайлар қарастырылмайды, себебі бастапқы жағдай
 біреу ғана, екінші қадамдағы шартты тиімді басқарулар ескеріле отырып, тиімді басқару бірден анықталады.
біреу ғана, екінші қадамдағы шартты тиімді басқарулар ескеріле отырып, тиімді басқару бірден анықталады.
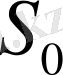 -ден
-ден
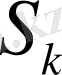 -ға дейін өтіп, тұтас үдерістің ізделініп отырған тиімді басқаруы алынады.
-ға дейін өтіп, тұтас үдерістің ізделініп отырған тиімді басқаруы алынады.
Р. Беллманның [1] көрсетуіндей, көп кезеңді үдерістің тиімді шешімін табу функционалдық теңдеудің шешімін табуға келтіріледі.
Шамасы х қаржы екі түрлі кәсіпорнын дамытуға жұмсалады делік. Егер бірінші кәсіпорнына у, екіншісіне х-у қаржы бөлінсе, онда кіріс тиісінше g(y) және h(x-y) -ті құрасын. Жалпы кіріс J максималды болатындай етіп қаржыны бөлу қажет. Қойылған есеп мақсат функциясының максималды мәнін табуға келтіріледі.
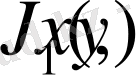 ,
,
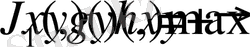 , (1)
, (1)

Егер g және h функциялары
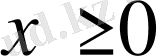 мәндерінде үздіксіз болса, мақсат функциясының максималды мәні барлық уақытта бар екендігі белгілі.
мәндерінде үздіксіз болса, мақсат функциясының максималды мәні барлық уақытта бар екендігі белгілі.
Сонымен max
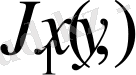 бір кезеңді үдерістегі мүмкін болатын максималды кірісті анықтайды. Кірістің бірлік өлшемі қаржының бірлік өлшемінен өзгеше болуы да мүмкін. Мысалы х теңге болса, g(y) адам-сағат мөлшері, машина қолданғанда үнемделген нәтижесі болуы да мүмкін.
бір кезеңді үдерістегі мүмкін болатын максималды кірісті анықтайды. Кірістің бірлік өлшемі қаржының бірлік өлшемінен өзгеше болуы да мүмкін. Мысалы х теңге болса, g(y) адам-сағат мөлшері, машина қолданғанда үнемделген нәтижесі болуы да мүмкін.
Екі кезеңді үдерісті қарастырайық. Бастапқы қаржы у кіріс g(y) -ті алуға жұмсалған шығыннан соң
 шамасына дейін кемиді
шамасына дейін кемиді
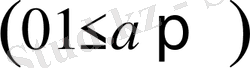 , сол сияқты (х-у) -те һ(х-у) кірісінен соң b(x-y) -ке дейін кемиді
, сол сияқты (х-у) -те һ(х-у) кірісінен соң b(x-y) -ке дейін кемиді
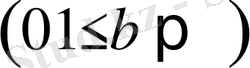 делік. Онда бір кезеңді үдерістен соң қалған қаржы
делік. Онда бір кезеңді үдерістен соң қалған қаржы
 үшін бөлісті қайта жалғастырамыз
үшін бөлісті қайта жалғастырамыз
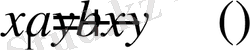 ,
,
 ,
,
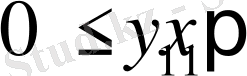 .
.
Бұл бөліс нәтижесіндегі кіріс
 , онда толық кіріс
, онда толық кіріс
.
Демек, максималды толық кіріс осы функцияның
 және
және
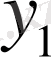 айнымалылары бойынша алынатын максимумынан турады
айнымалылары бойынша алынатын максимумынан турады
.
,
.
N кезеңнен тұратын үдерісте операция N рет қайталанады, толық кіріс функциясы былай анықталады
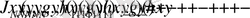 , (2)
, (2)
мұндағы бірінші, екінші, . . . , (N-1) -ші кезеңдерде әрі қарай бөлініске түсетін шамалар келесі қатынастармен анықталады:
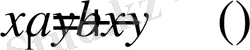 ,
,
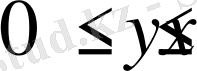 ;
;
 ,
,
 ;
;
. . . (3)
 ,
,
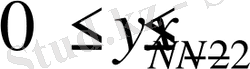 ,
,
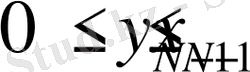 .
.
Есепті кезеңдерге бөліп, тиімділік қағидасымен N кезеңді үдерісте шешеміз. N кезеңді үдерістегі толық кірістің максималды мәні тек N-нен және бастапқы х шамасынан тәуелді болатындықтан
деп аламыз. Онда бір кезеңді үдерісте
 . (4)
. (4)
Екі кезеңдік үдерісте алғашқыдан қалған
 шамасын тиімді етіп бөлу қажет. Демек
шамасын тиімді етіп бөлу қажет. Демек
 тиімді таңдалғандағы кіріс
тиімді таңдалғандағы кіріс
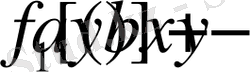 , ал екі кезеңді үдеріс үшін толық кіріс
, ал екі кезеңді үдеріс үшін толық кіріс
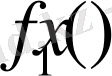 және
және
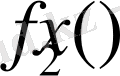 функцияларын байланыстыратын
функцияларын байланыстыратын
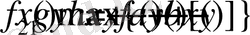 (5)
(5)
рекурентті қатынасымен өрнектеледі. Осылайша тұжырымдай отырып, N кезеңді үдеріс үшін негізгі функцио-налдық теңдеуді аламыз:
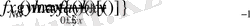 ,
,
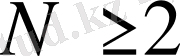 (6)
(6)
Мұнда әрбір кезең есептеулерінде
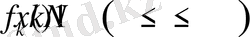 мен бірге
мен бірге
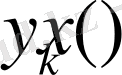 -те анықталады.
-те анықталады.
Сонымен динамикалық бағдарламалау есебін функционалдық теңдеулер әдісімен шешкенде N өлшемді есепті N тізбектен тұратын бір өлшемді есептерге келтіреміз.
Динамикалық бағдарламалауда үдеріс соңғы жағдайдан бастапқы жағдайына қарай өрбитіндіктен, бұған тән дискретті үдерісті өрнектейтін функционалдық теңдеу:
, (7)
f-үдеріс мақсаты (кіріс, пайда т. б) ; N-кезеңдер саны; х-айнымалы, жүйенің N-ші қадамдағы сипаттаушысы;
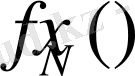 - белгінің нәтижелік мәні, тиімділік қағидасымен алынған;
- белгінің нәтижелік мәні, тиімділік қағидасымен алынған;
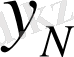 - басқарушы айнымалы, нәтижелік белгінің мәні тәуелді болатын;
- басқарушы айнымалы, нәтижелік белгінің мәні тәуелді болатын;
 - белгінің шамасы; N-ші кезеңде алынған, 0 мен х аралығында;
- белгінің шамасы; N-ші кезеңде алынған, 0 мен х аралығында;
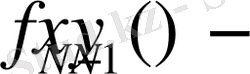 - нәтижелік белгінің тиімді мәні
- нәтижелік белгінің тиімді мәні
 жағдайынан бастап қалған N-1 кезеңдерден өткеннен соңғы.
жағдайынан бастап қалған N-1 кезеңдерден өткеннен соңғы.
N-ші кезеңдегі тиімді басқару
 делік. Онда жүйенің (N-1) -ші кезеңдегі жағдайының функционалдық теңдеуі:
делік. Онда жүйенің (N-1) -ші кезеңдегі жағдайының функционалдық теңдеуі:
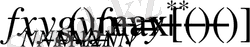 , (8)
, (8)
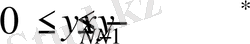 ,
,
себебі
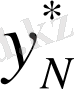 шамасын N-ші кезеңде таңдауға байланысты бастапқы х шамасы
шамасын N-ші кезеңде таңдауға байланысты бастапқы х шамасы
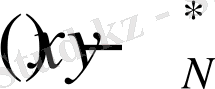 -ге дейін кеміген.
-ге дейін кеміген.
2. 2. Р. Беллманның оңтайлау принципін пайдаланып
есеп шығару
Бүтін сандық программалау есептерінің бірі болып табылатын, ізделінетін есептің экстремалдық шешімін кейбір белгілі сандар жиынтығын алмастыруын сипаттау арқылы алынатын есеп үлкен қызығушылық танытады. Бұл есептер комбинаторлық типті есептер деген атқа ие болды.
Бүтін сандық типтің сызықтық есебін қию əдісімен шешу барысында міндетті түрде олардың кемшіліктеріне көңіл аудару керек, себебі практикалық есептің шешімін алуға мүмкіндік бермейтін жағдайды туғызуы мүмкін. Біріншіден, бұл бірнеше рет бағаларды тізбектеп дəлдеу əдісінің қолданылуымен жəне осымен байланысты есептеу қателіктерімен; екіншіден,
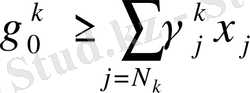 формуласы бойынша қосымша сызықтық шектеулерді құрумен түсіндіріледі, мұндағы
формуласы бойынша қосымша сызықтық шектеулерді құрумен түсіндіріледі, мұндағы
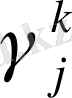 қателіктер мəні. Мұндай кемшіліктер варианттардың тізбектелген талдауы əдісінде кездеспейді.
қателіктер мəні. Мұндай кемшіліктер варианттардың тізбектелген талдауы əдісінде кездеспейді.
Варианттардың тізбектелген талдауы əдісінің схемасына Р. Беллман атымен байланысқан динамикалық программалау əдісі; Литтл, Суин, Карел [1] аттарымен байланысқан буындар мен шекаралар əдістері жатады. Варианттарды тізбектеп талдау əдісінің қию əдісінен айырмашылығы, бұл əдіс сызықтық программалау аппаратын мүлдем пайдаланбайды жəне есептеу қателіктерін жібермейді.
Динамикалық программалау əдісі - бұл басқарудың жіберуші дискретті жиынымен берілген математикалық программалау есептерінің тиімді шешімін жылдам табуға мүмкіндік беретін құрал, яғни əр түрлі шешімдерді алып келетін, беталыстың əр түрлі варианттарының кейбір көрсеткіштерінің арасынан ең жақсысын таңдап алу керек. Осы тəріздес кез келген есептің шешімін мүмкін болатын барлық варианттарды теру жолымен жəне олардың арасынан ең жақсысын таңдау арқылы алуға болады. Бірақ мұндай теру қиындық туғызуы мүмкін. Мұндай жағдайда тиімді шешімді қабылдау процесі қадамдарға бөлініп, динамикалық программалау əдісімен зерттелуіне мүмкіндік алады. Динамикалық программалау əдісін пайдаланып жалпы түрде есептің шешімін қарастырайық [2] .
Айталық, тиімдеу процесі
n
қадамға бөлінсін делік. Əрбір қадамда екі типті айнымалыларды анықтау қажет - s жағдай айнымалысын жəне x басқару айнымалысын. s айнымалысы жиынның берілген k-қадамда қандай жағдайларда болатын мүмкіндігін анықтайды. s айымалысына байланысты осы қадамда кейбір
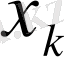 айнымалысымен сипатталатын басқаруды пайдалануға болады. х басқаруын k-қадамда пайдалану
айнымалысымен сипатталатын басқаруды пайдалануға болады. х басқаруын k-қадамда пайдалану
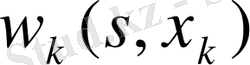 кейбір нəтижесін береді жəне жүйені кейбір жаңа
кейбір нəтижесін береді жəне жүйені кейбір жаңа
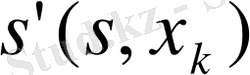 жағдайына ауыстырады. Сонымен, жүйе ауысқан
жағдайына ауыстырады. Сонымен, жүйе ауысқан
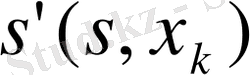 жағдайы берілген s жағдайымен таңдалынған
жағдайы берілген s жағдайымен таңдалынған
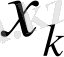 басқаруына байланысты деп жəне жүйе s жағдайына қандай жолмен ауысқанына байланысты емес деп болжаймыз. k-шы қадамда əрбір мүмкін болатын жағдай үшін мүмкін болатын барлық басқарулар ішінен
басқаруына байланысты деп жəне жүйе s жағдайына қандай жолмен ауысқанына байланысты емес деп болжаймыз. k-шы қадамда əрбір мүмкін болатын жағдай үшін мүмкін болатын барлық басқарулар ішінен
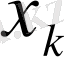 тиімді басқаруы таңдалынады, оның k-шы мен n-ші қадамдар аралығында алынатын нəтижесі тиімді болу керек.
тиімді басқаруы таңдалынады, оның k-шы мен n-ші қадамдар аралығында алынатын нəтижесі тиімді болу керек.
Ары қарай k-қадамды жүзеге асыру нəтижесінде белгілі бір кіріс немесе ұтыс қамтамасыз етіледі деп санаймыз, ол s жүйесінің алғашқы жағдайы мен таңдалынған
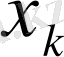 басқаруына байланысты жəне
басқаруына байланысты жəне
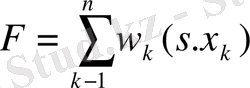 тең болады. Сонымен, біз екі шартты тұжырымдадық, ол шарттарды қарастырылатын динамикалық программалау есебі қанағаттандыру қажет. Əдетте бірінші шартты - салдары жоқ шарт, ал екіншісін - есептің мақсаттық функциясының аддитивті шарты деп атайды.
тең болады. Сонымен, біз екі шартты тұжырымдадық, ол шарттарды қарастырылатын динамикалық программалау есебі қанағаттандыру қажет. Əдетте бірінші шартты - салдары жоқ шарт, ал екіншісін - есептің мақсаттық функциясының аддитивті шарты деп атайды.
Бірінші шарттың динамикалық программалау есебі үшін орындалуы Беллманның тиімді принципін тұжырымдауға мүмкіндік береді. Мұны орындамай тұрып, басқарудың тиімді стратегиясына анықтама берейік. Басқарудың тиімді стратегиясы деп
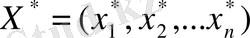 басқарулар жиынтығын түсінуге болады.
басқарулар жиынтығын түсінуге болады.
Тиімдеу принципі. Шартты тиімдеу, немесе шартты тиімді басқару, деп аталатын есепті шешудің бірінші кезеңінде Беллман функциясы мен соңынан басталатын əрбір қадамдағы барлық мүмкін болатын жағдайлар үшін тиімді басқарулар ізделінеді.
Жоғарыдағыны практикалық жүзінде іске асыру үшін тиімділеу принципінің математикалық тұжырымын беру қажет. Ол үшін кейбір қосымша белгілеулерді енгіземіз.
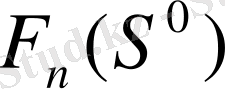 -пенен басқарудың тиімді стратегиясы
-пенен басқарудың тиімді стратегиясы
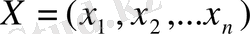 іске асыра отырып, жүйенің алғашқы
іске асыра отырып, жүйенің алғашқы
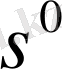 жағдайынан соңғы
жағдайынан соңғы
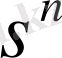 жағдайына көшкендегі n қадамдарынан алынған ең үлкен кірісті белгілейік, ал
жағдайына көшкендегі n қадамдарынан алынған ең үлкен кірісті белгілейік, ал
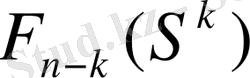 -пенен қалған n-k қадамдарындағы басқарудың тиімді стратегиясын іске асыра отырып, жүйенің кез келген
-пенен қалған n-k қадамдарындағы басқарудың тиімді стратегиясын іске асыра отырып, жүйенің кез келген
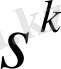 жағдайынан соңғы
жағдайынан соңғы
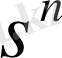 жағдайына көшуде алынған ең үлкен кірісті белгілейік.
жағдайына көшуде алынған ең үлкен кірісті белгілейік.
Сонда
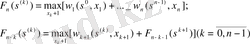 (1)
(1)
Соңғы көрсетілген өрнек тиімді принципті математикалық жазуды көрсетеді жəне Беллманның негізгі функционалдық теңдеуі, немесе рекурренттік сəйкестік, деп аталынады. Берілген теңдеуді пайдаланып, динамикалық программалау есебінің шешімін табамыз. Берілген процесті толығырақ қарастырайық.
(1) рекурренттік сəйкестігінде k=n-1 деп алып, келесі функционалдық теңдеуді аламыз:
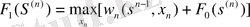 (2)
(2)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz