Жай бөлшектерге амалдар қолдану: теориясы, қасиеттері және оқыту әдістемесі


Ж. Досмұхамедов атындағы педагогикалық колледжі
Курстық жұмыс
Тақырыбы:
«Жай бөлшектерге амалдар қолдану»
Орындаған: Наженова С. А.
Тексерген: Сапахова Г. М.
Орал - 2014ж.
Мазмұны
Кіріспе . . . 3
1. Жай бөлшектер туралы түсінік
1. 1 Бөлшектер ұғымы және олараға амалдар қолдану . . . 5
1. 2 Аралас сандар және бөлшектердің түрлері . . . 8
2. Жай бөлшектерге амалдар қолданып есептер шығару
2. 1 Жай бөлшектер мен аралас сандарға амалдар қолдануға есептер шығару . . . 17
2. 2 Жай бөлшектің негізгі қасиеті . . . 21
2. 3 5-сыныпта математика сабағы: «Жай бөлшектер» . . . 24
Қорытынды . . . 27
Пайдаланылған әдебиеттер тізімі . . . 29
Кіріспе
Математиканы оқытуда, біздіңше, қарапайым түсініктерді қалыптастыру мен дамыту жолдарын анықтаудың негізі ретінде оқушының жеке басының іс-әрекеттін қасиетіне деген қызығушылықтың ыңғайынан алған абзал.
Қарапайым түсініктерді қалыптастыру оқушылардың танымдық сұранысының объективті көрінісі ретінде, яғни олардың шығармашылық есептерді орындауда білімі, біліктілік және машақтарға ие болуларына бағытталған қауырт оқу танымдық іс-әрекеті ретінде көрінеді. Осындай іс-әрекетті басқаратын, қарастырылып отырған математикалық жағдайдың (ол әртүрлі есеп, тапсырмалар, проблемалық мәселелер болуы мүмкін) шешімін табуда оқушының іс-әрекетінің шығармашылық сипатында өрбуіне жетелейтін әдістемені жасау қажеттілігінен туып отыр.
Натурал сандарды көбейту деп бірдей қосылғыштардыц қосындысын табу амалып айтады. Қосылғыш ретін-де қайталанатын сан көбейгіш, оның неше рет қосылатынын көрсететін сан көбейткіш, ал амал нәтижесі көбейтінді деп аталады. Көбейгіш пен көбейткішті жалпы алғанда көбейткіштер деп те атайды. Мыс., 6X5=30, 6 -кобейгіш. 5 - көбейткіш, 30 - көбейтінді. Көбейту амалы да ауыстырымдылық, терімділік және үлестірімділік (дистрибутивтілік) заддарына бағынады. Ертедегі Индияда көбейту амалы сол жағынан басталып орындалатын. Қазіргі үйреншікті тәсіл 15 ғ-дан бастап қолда-нылған. Көбейту таңбасы әуелде нүкте (•) түрінде (15 ғ. ), кейін онымен қатар кірес (X) түрінде (17 ғ. ) жазылатын болған.
Екі көбейткіштің көбейтіндісінеп сол кобейткіштердің бірі арқылы екіншісін табу амалы бөлу деп аталады. Бөлінетін сан бөлінгіш, оны белетiн сан бөлгіш, белу нәтижесі бөлінді деп аталады. Мыс., 12:3=4, 12 - бөлінгіш, 3 - бөлгіш, 4 - бөлінді. Бөлу амалы - көбейту амалына кері амал. Белу амалы бүтіндей болу және қалдықпен бөлу деп екі турге бөлінеді. Қалдықпен бөлу дегеніміз - бөлгішпен кобейтіндісі берілген бөлінгіштен артпайтын ең үлкен бүтін санды табу деген сөз. Бүл іздеп отырған сан толымсыз бөлінді дсп аталады. Бөлінгіштің толымсыз бөлінді мен бөлгіш кебейтіндісінен айырмасы қалдқ деп аталады, ол - белгіштен әрқашан да кем болады. Мыс., 21-ді 4-ке бөлгенде, толымсыз бөлінді 5, қалдық 1 болады, яғни 21=4x5+1. Белудің қазіргі қолданылатын тәсілін 15 ғ-да итальян ғалымдары ойлап шығарған. Бөлу таңбасын (: ) алғаш қолданған (1633) - ағылшын ғалымы Джонсон.
Теңдік таңбасын ( = ) алғаш енгізген (1557) ағылшын дәрігері - Роберт Рекорд. Арифметикалық амалдардағы қазіргі таңбалар тек 17 ғ-дың ақырында ғана барлық елдерде қолданыла бастаған.
Математиканы оқыту мақсаттарының бірі - оқушыларға саналы, жүйелі және баянды білім беру. Ал білім нәрселер мен құбылыстардың елеулі белгілері мен олардың байланыстары туралы ғылым тағайындайтын ұғымдардан құралады. Ф. Энгельстің анықтауынша ұғым мен қимылдың өзі - ойлау. Ұғым арқылы адам ойлайды. Ой болмысты бейнелейді. Ойлау арқылы адам болмысты танып біледі.
1. Жай бөлшектер туралы түсінік
1. 1 Бөлшектер ұғымы және олараға амалдар қолдану
Бөлшек, арифметикада -бірліктің (бір бүтіннің) бір не бірнеше тең үлестерінен құралған сан. Ол (немесе m/n) белгісімен өрнектеледі, мұндағы m - Бөлшектің алымы, ол бірліктен алынған үлес санын көрсетеді, ал n - Бөлшектің бөлімі, ол бірліктің тең бөлікке бөлінгендігін көрсетеді. Бір санды екінші санға бөлгеннен шығатын сан бөлінді деп аталады. Алымы бөлімінен кіші Бөлшек дұрыс Бөлшек деп, ал алымы бөліміне тең не одан үлкен Бөлшек бұрыс Бөлшек деп аталады. Бөлімі 10 санының бүтін дәрежесі болатын Бөлшек ондық бөлшек деп аталады. Ондық Бөлшек бөлімсіз жазылады. Оның бөлімінде қанша нөл болса, алымының оң жағынан сонша цифр (орын) үтір арқылы ажыратылады. Мысалы, (ал тізбекті Бөлшек жайлы үзіліссіз бөлшек мақаласын қ. ) . Бөлшек туралы алғашқы түсінік ежелгі Вавилонның ескілікті жазуларында кездеседі. Вавилондағы “сексагезимал Бөлшек” деп аталатын, яғни бөлімі 60-тың дәрежесі болатын Бөлшектің ежелгі арифметикада ерекше маңызы болған. Бірлікті 60 және 3600 = 602 үлеске бөлу әдісі қазіргі кезге дейін сақталған. Мысалы, сағат не градус 60 мин-қа (), ал әрбір минут 60 с-қа бөлінеді. Бөлшекке амалдар қолдану әдісі Мысырдағы Ахмес папирусында (б. з. б. 2000 - 1700 ж. ) кездеседі. Онда Бөлшекті тек түрінде ғана болады деп есептеп, кез келген Б-ті өзара тең Б-тердің қосындысы түрінде жазуды ұсынған. Мысалы, . Бөлшектің осы заманғы белгіленуі ежелгі үнділерде пайда болған. “Бөлшек” термині Еуропаға 1202 жылы арабтардан Леонардо Пизанскийдің еңбегі арқылы енген.
Ерте кезде адамдарға сауда - саттық және түрлі есептеу жұмыстарында бөлшектер мен үлестерді есептеу қажет болған. Алғашында математикада бөлшектерді «сынық сандар» деп атаған. Бөлшектер туралы түсініктің дамуында үш түрлі бөлшектер ұғымы қалыптасқан.
1. Бірлік бөлшектер (аликвоттық бөлшектер)
2. Жүйеленген бөлшектер. Жүйеленген бөлшектің алымы кез келген бүтін сан, бөлімі тек 10 санының немесе 60 санының дәрежелері ғана болған.
3. Жалпы түрдегі бөлшек. Жалпы түрдегі бөлшектің алымы да, бөлімі де кез - келген натурал сан болады.
Бөлшектердің мұндай әртүрлілігі есептеу және өлшеу жұмыстарында көптеген қиындықтар туғызады. Бөлшек ұғымының дамуы ғылым мен сауда - саттық жұмыстары өркендеген елдерде: Мысырда, Вавилонда, Үндістанда және Римде қалыптасады. Ертеде әр түрлі елдер бөлшек сандарды белгілеуде өздерінің түрліше символдарын енгізді.
Арифметикалық амалдар - берілген сандар бойынша тиісті шартты қанағаттандыратын басқа бір санды табу әдісі. Мектеп арифметикасында натурал сандар меп оң бөлшектерді қосу, азайту, көбейту, бөлу амалдары қарастырылады. Берілген натурал сандарды қосу деп сол сандарда қанша бірлік болса, сонша бірліктерден қүралған санды табу амалын айтады. Берілген сандар қосылғыштар, ал қосу нәтижесі қосынды деп аталады. Мыс., 5+7+8=20, мүндағы 5, 7, 8 - қосылғыштар, 20 - қосынды. Қосу амалы ауыстырымдылық (коммутативтілік) және терімділік (ассоциативтілік) заңдарына бағынады. Ерте кезде сандарды сол жақтан бастап қосатын болған. Өзімізге үйреншікті түрдегі қосу тәсілі жәпе онын таңбасы ( + ) 15 ғ-да енгізілген. Азайту амалы деп берілген қосынды мен бір қосылғыш бойьшша екінші қосылғышты табу амалын айтады. Берілген қосынды азайғыш, берілген қосылғыш азайтқыш, ал азайту нәтижесі айырма деп аталады. Сонымен, азайту амалы - қосу амалына кері амал. Мыс., 15-8=7; 15 - азайғыш, 8 - азайтқыш, 7 - айырма. Ертеректе азайту амалы да қазіргіге керісінше, сол жақтап басталып орындалатын. Қазіргі үйреншікті тәсіл Европада 15 ғ-дан бастап қолданылған. Азайту тацбасының ( -) да шыққан кезі - сол уақыт.
Нәрселердің кез келген топтарын санай білу қажет болғандықтан натурал сандар пайда болды:1, 2, 3, 4 . . . Адамзаттың мәдени дамуының алғашқы кезеңдерінде натурал қатар азынаулақ сандардан құралған. Онан әрі даму барысын да натурал қатарға жаңа және үлкен сандар қосылып отырды. Алайда талай уақыт бойы натурал қатар шектеулі деп есептелді, яғни адамдар қандай да бір ақырғы, ең үлкен сан бар деген ұғымда болды.
Мысалы, Ежелгі Русьте «тьма» (сансыз көп) деп аталған 104 санын ақылға сыймайтын үлкен сан деп білген кез болған. «Тьма тем» түпсіз тұңғиық деп аталған 1012 саны туралы ескілікті орыс жазбаларында былай делінген: «Адам ақылы жететін бұдан үлкен сан болмайды . . . ». Алайда қоғамдық даму барысында адам ақылы жетуге тиісті сандар үлкею үстіне үлкейе түсті де, натурал қатарда ең үлкен сан болады- мыс деген ойдан бас тартуға тура келді, бірақ та бұл ақиқатты әр халық әр уақытта ұғынды.
Ежелгі Грекияның асқан ұлы ғалымы Архимед б. э. дейінгі III ғасырла «Псаммит», яғни «Құм түйіршіктерін есептеу» деп атап, арифметикаға арналған кішкене кітапша жазды, сол кітапшасында ол кейбір адамдардың жалған пікірін, яғни жер бетіндегі құм түйіршіктерінің көптігі сондай, оны сөзбен жеткізуге болмайды, сірә, онан үлкен сан болмайды-мыс деген пікірін теріске шығарды. Архимедтің дәлелдеуінше, бүкіл дүние кеңістігі, бүкіл әлем құм түйіршіктерімен толтырылған болса, онда түйіршіктер саны 1063 санынан, яғни 63 нолі бар бірліктен құралған саннан артпайды және, әрине, бұдан да артық, мейлінше үлкен сандар бар. Сонымен Архимед «Псаммит кітапшасында» санау процесін шектеусіз жүргізе беруге болатындығын, натурал қатар шексіз екенін дәлелдеді. Алайда бұл идея көпшілікке аян болу үшін жүздеген жыл уақыт керек болды.
1063 саны үлкен сандарды қазіргіше жазудың мысалы болып табылады. n нолі бар бірлік түріндегі әрбір сан 10n түрінде қысқаша жазылады және онның n-ші дәрежесі деп аталады. Мысалы, жүз - онның екінші дәрежесі (102 =10*10=100), мың - онның үш дәрежесі (103=10*10*10=1000) т. с. с. Дәреже ұғымын пайдаланып, үлкен сандарды тек қысқаша жазу ғана емес, оларды анағұрлым қысқарақ атауға болады, ал осы заманғы ғылым мен техникада кездесетін үлкен сандар көбінесе жуық сандар болады.
1. 2 Аралас сандар және бөлшектердің түрлері
Бөлшектер үш типке бөлінеді: 1) бірлік бөлшектер немесе үлестер, мысалы 1/2 1/3 1/4 …т. с. с. ; 2) системалық бөлшектер, яғни бөлімі берілген бөлшектер түрі үшін қабылданған санның дәрежесі болып келетін бөлшектер, мысалы бөлімі 10-ның немесе 60-тың дәрежелері болатын бөлшектер. Бөлімі 60, 60•60, 60•60•60 сандар болып келетін осы сияқты бөлшектерді ерте кезде вавилондық кемеңгерлер пайдаланған және әр түрлі операциялар қолданған 3) жалпы түрдегі бөлшектер, яғни алымы да, бөлімі де кез келген бүтін сан болуы мүмкін бөлшектер. Алымы бөлімінен артық бөлшектер орта ғасырда «жалған» бөлшектер деп атап, оларды дұрыс бөлшектерге, яғни «нақты» деп бөлшектреге кереғар қойған. Тек 17 ғасырдың екінші жартыжсында бөлшектерді жалған және нақты деп бөлмейтін болған. Бөлшектің қазіргі жазудың бастапқы нұсқасы 8 ғасырда Үндістанда ойланып табылған.
Сонан кейін бұл жазу Орта Азия елдеріне, олардан Европаға тараған.
Ондық бөлшекті жазғанда нөл цифры жиі қолданылады. Нольдың шығу тегінің, атауының, таңбасының қызық тарихы бар.
Абсолютті позициялық нумерацияның қай - қайсысында болса да санда жоқ разрядты білдіретін таңба қажет болады. Алпыстық позициялық нумерация алғаш өріс алған ежелгі Вавилонның өзінде ондық, кейініректе алпыстық та разрядтарды бір-бірінен айыруға арналған таңба біздің эрамызға дейінгі 5 ғасыр шамасында пайда болған, алайда бұл ьаңба үнемі қолданылып отырмаған.
Алпыстық бөлшектерді пайдаланған грек астрономдары разрядтарды бір-бірінен айыру үшін айрықша таңба қойған. Ол таңба «О» әрпі тәрізді болған. Ежелгі үндістанда 7- ғасырдың өзінде-ақ ондық позициялық санау системасы қолданылған еді де, онымен бірге ноль үнемі қолданылып отырған, оны нүктемен, кішкене дөңгелекпен белгілеген. Кейбір ғалымдардың пікірінше нольды дөңгелекпен белгілеуді гректер енгізді.
Үнділер нольды «сунья» деп атаған, бұл- санда разряд жоқ деген мағынадағы «бос» деген сөзді білдіретін. Европалықтар ондық позициялық санау системасын арабтардан үйренген, ал арабтар Үндінің «сунья» деген сөзін арабша «аз-сифр» деп аударған. Сондықтар 17 ғасырға дейін ноль «цифр» деп аталып келген. Магницкий де өзінің «Арифметикасында» нольды осылайша атаған. Европалықтар әуелде үнді арифметикасының нольдың бір құпия сыры бар деп есептеді. Сондықтан, құпия жазу атаулының бәрін «цифр» немесе «шифр» деп атайтын. «Ноль» деген сөз латынның «Nulla» «ешқандай» деген сөзінен шықты.
Қазіргі кездегі түсінігімізше ноль - разрядтарды айыру үшін қолданылатын таңба ғана емес, ол сан, басқа сандар сияқты, оны қосуға, азайтуға, көбейтуге, бөлуге болады. Тек міндетті бір ғана шарт- нольге бөлуге болмайды.
Есептеуде жай бөлшектерді ондық бөлшектерге айналдырып алу көп жағдайда тиімді болатын көрінеді, өйткені ондық бөлшектерге амалдар қолдану оңайлау болады.
Жай бөлшектерді ондық бөлшектерге айналдыру ісімен тіпті XVII ғасырдың өзінде итальян математигі Бонавентура Кавальери, ағылшын математигі Джон Валлис және басқа да ғалымдар шұғылданған. Бұл ғалымдар шексіз бөлу процесімен байланысты болатын периодты бөлшектерге кездескен. XVIII ғасырда периодты бөлшектер неміс ғалымы Иоганн Ламберт және Леонард Эйлер де қарастырып зерттеді. Периодты бөлшектердің толық теориясын XIX ғасырдың басында неміс математигі Карл Фридрих Гаусс жасады.
Шексіз қайталай беретін цифрлар тобына қатысты қолданылатын «период» термині гректің «периодос» - айналма, шеңбер бойымен деген сөзінен шыққан.
Ерте заманғы құрылыстарды - пирамидаларды, сарайларды, ғибатханаларды салғанда қолданылған плиталар мен кірпіштердің беттері үшбұрыш, төртбұрыш, квадрат және басқа да фигуралар тәрізді болатын. Жер танаптарын бөлгенде, оларды өлшегенде адамға осындай фигуралар кездесетін. Әр түрлі геометриялық фигуралармен таныса келе, адам олардың жалпы қасиеттерін де аңғара бастады. Осылайша, бірте-бірте фигуралар жөніндегі ғылым - геометрия қалыптаса бастады. Ежелгі Грекияда Пифагор мектебінде геометрия өрлей дамып, биік дәрежеге көтерілді.
Пифагор және оның шәкірттері тек геометрияны ғана емес, арифметиканы да дамытты, сонда олардың сандар жөніндегі ілімі геометриялық фигуралар жөніндегі іліммен тығыз ұштасып отырды. Пифагоршылар ұсақ сүйектерден немесе түйіршік тастардан әр түрлі фигуралар жасады, сандарды геометриялық фигуралар жасай топталатын нүктелер түрінде кескіндеді. Сандарды осылайша кескіндеу пифагоршылардың сандар қасиеттерін зерттеудегі жұмысын жеңілдетті. Геометриялық фигураларды пайдаланып кескіндеуге болатын сандар ілгері уақытта фигуралық сандар деп аталатын болды. Фигуралық сандар тек пифагоршыларда ғана емес, басқа да грек ғалымдарында: Эратосфенде, Никомахта, Диофантта және басқа ғалымдарда кездеседі. Үнді математиктері де фигуралық сандармен айналысты.
Фигуралық сандардың ең қарапайымдары - үшбұрыштық сандар: 1; 3; 6; 10; 15; 21; 28; 36; . . .
Үшбұрыштық сандардың тізбегін былайша жасауға болады: натурал сандар қатарынан: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 11, 12, . . .
әуелі 1 санын, сонан кейін алғашқы екі санның қосындысын (1+2=3), онан әрі алғашқы үш санның қосындысын, алғашқы төрт санның қосындысын т. с. с. аламыз.
Квадраттық сандар деп: 1, 4, 9, 25, 36; . . .
Қатарының сандарын, яғни 1, 2, 3, 4, 5, 6, . . . натурал сандардың квадраттарын атайды. Сонымен квадраттық сандар қатарындағы n-ші сан n2 болады.
Әр түрлі практикалық есептерді шығарғанда бір тектес шамаларды өзара салыстыруға, бүтін немесе бөлшек сандармен өрнектелген шамалардың қатынасын табуға тура келеді. Ерте заманда және бүкіл орта ғасырлар бойында дерлік тек натурал санды ғана, санау нәтижесінде шыққан бірліктер жиынын ғана сан деп түсінетін. Ал бір санды екінші санға бөлу нәтижесі болып табылатын қатынас сан болып саналмайтын.
Бірақ Орта Азия математиктері Омар Хайям мен Насыреддин ат-Туси еңбектерінде қатынас та сан, бүтін сандарға қолданылатын амалдарды қатынастарға да қолдануға болады деген пікір баяндалған болатын.
Санның жаңа анықтамасын айқын түрде тұңғыш рет XVII ғасырда ағылшынның дана ғалымы Исаак Ньютон баяндап берді. Ол өзінің «Жалпыға бірдей арифметикасында» былай деп жазды: «Біз сан деп бірліктер жиынын ғана түсінбей, бір шаманың бірлік ретінде алынған басқа бір шамаға дерексіз қатынасын сан деп түсінеміз».
Бұл анықтама бүтін сандарды да, бөлшек сандарды да қамтиды.
Аралас сан - бүтін және бөлшек бөлігі бар сан, мысалы,
Аралас санның бөлшек бөлігі дұрыс бөлшек болады. Аралас сандарды қосқанда бүнін сандар өзара және бөлшек бөліктері өзара жеке-жеке қосылап жазылады.
Мысалы,
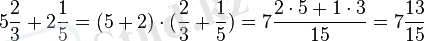
Аралас сандар азайтылғанда бүтін сандардан бүтін сандар, ал бөлшек бөлігінен бөлшек бөлігі өзара жеке-жеке шегеріледі.
Мысалы,
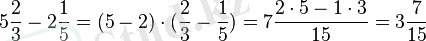
Көбейту және бөлу амалдары да бөлшектердің сәйкес амалдарына ұқсас жүзеге асырылады.
Бүтін сан - натурал сандардың айырымы түрінде өрнектеуге болатын сан. Натурал сан, теріс натурал сан, немесе нөл бүтін сан болып есептеледі. Барлық бүтін сандар жиыны 2 болып белгіленген (бұл немісше "zahl - сан" деген сөзінің алғашқы әрпі) .
Бөлшек бөлік - a нақты санымен оның бүтін бөлігінің айырымы: a-[a], мұндағы а нақты сан, [a] - a саныңың бүтін бөлігі, мысалы ~[5, 6] = 5. Бөлшек бөлігі - {a} белгісімен белгіленген: 0 < {a} < 1
Дұрыс бөлшек - алымы бөлімнен кіші болатын бөлшек, яғни
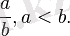 Мысалы,
Мысалы,
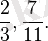 Егер алымы бөлімінен үлкен болса, яғни
Егер алымы бөлімінен үлкен болса, яғни
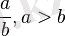 , онда бұл - бұрыс бөлшек деп аталады. Мысалы:
, онда бұл - бұрыс бөлшек деп аталады. Мысалы:
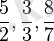
Жай бөлшектерді көбейткенде бөлшектерді қысқартып, болған соң, көбейту керек.
Бөлшекті натурал санға көбейту (немесе керісінше) . Бұл есеп ой қозғауда қарастырылды ғой, сондықтан ережесін оқушылардың өздеріне қорытуға жетелеу керек:
Ереже: Натурал санды бөлшекке көбейткенде натурал сан бөлшектің алымына көбейтіліп, көбейтінді бөлшектің алымы ретінде алынады да, бөлі-мі өзгеріссіз сол қалпында жазылады.
Аралас сандарды көбейту.
Алдын ала мысалды жазып, шығарылу жолын көрсетіп қойып, оқушыларға көбейтінді бөлшектің қалай шыққандығы туралы ой тастау керек. Есепке қарап отырып оқушылар аралас сандарды бұрыс бөлшекке айналдырғанын байқап, ережені оқушылардың өздеріне қорытуға жетелеу керек.
Ереже: Аралас сандарды алдын ала бұрыс бөлшекке айналдырып, бөлшекке көбейту ережесі бойынша көбейтеміз.
Периодты бөлшектердің қасиеттерін зерттеу.
Міндеттері:
- бөлшектің бөлімі мен периодының ұзындығы арасындағы байланысты қарастыру;
- Периодты бөлшектерге әртүрлі амалдар қолдана отырып, қандай да бір қасиеттерді байқау.
Жұмыста периодты бөлшектердің оқушылардың барлығы біле бермейтін қасиеттері, олардың дәлелдемелері қарастырылады. Периодты бөлшектермен әртүрлі амалдар орындай отырып, олардың кейбіреулерінде ортақ қасиет орындалатыны байқалды және құпияның түп төркінін іздеуде біз, оқушылар біраз қызықты нәрселерге жолықтық, беттері ашылмай шаң басқан біраз кітаптардыңбетін аштық.
Мынадай 3 мысалды қарастырып көрейік:
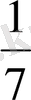 =0, 142857142857 . . . ,
=0, 142857142857 . . . ,
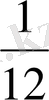 =0, 8 . . . ,
=0, 8 . . . ,
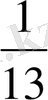 =0, 076923076923 . . . ,
=0, 076923076923 . . . ,
Біз көріп тұрғандай, 1/7 және 1/13 бөлшектерінің периодтары бірден үтірден кейін басталады және алты саннан тұрады (142857 және 076923), ал 1/12 бөлшегінде үшіншісінен басталады және жалғыз 3 цифрынан тұрады. Зер сала қарап, талқыласақ, кейін тағы бір жағдайды көруге болады. N=142857 (1/7 бөлшегінің периоды) деп алып, оны 2, 3, 4, . . . сандарына көбейтіп көрейік:
N2 =285714, N3 =428571,
N4 =571428, N5 =714285,
N6 =857142, N7 =.
Біз көріп тұрғандай, алдынғы бесеуі N санының цифрларын «шеңбер бойы алмастыруы» арқылы жасалған: санның соңындағы бірнеше цифры алға қарай көшеді; ал 7N бірыңғай тоғыздықтардан тұрады. Енді тура соны 1/13 бөлшегінің периодына жасап көрейік (N=076923) :
N2=153846, N3=230769,
N4=307692, N5=384615,
N6=461538, N7=538461,
N8=615384, N9=692307,
N10=769230, N11=846153,
N12=923076, N13=.
Бұл жерде сәл өзгешелеу, бірақ бәрібір қызықты, жазылғандардың бесеуі (3N, 4N, 9N, 10N, 12N) N санының цифрларының орындарын алмастыру арқылы жасалады, ал басқа алтауы ( 2N, 5N, 6N, 7N, 8N, 11N ) бір-бірінен шеңбер бойы алмастыру арқылы жасалады да, аяғында 13N бірыңғай тоғыздықтардан жасалады.
Тағы да мынаны байқауға болады. Егер жоғарыда жазылып кеткен алты таңбалы сандардың санынан өзге кез-келгенін алсақ, және тең ортасынан бөліп, әрқайсысыларын бір-біріне қоссақ 999 саны шығады; мысалы, 142+857=999 және т. б.
Көріп тұрғандай, периодтық бөлшектердің көптеген сырлары бар. Олардың көбі әлі жұмбақ күйінде. Жоғарыда айтылған қасиеттің сырын ашып көрелік.
1-теорема. Егер
 натурал саны 2-ге де, 5-ке де бөлінбесе,
натурал саны 2-ге де, 5-ке де бөлінбесе,
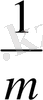 -ге тең ондық бөлшектің периоды бірден үтірден соң басталады. Оның периодтың ұзындығы
-ге тең ондық бөлшектің периоды бірден үтірден соң басталады. Оның периодтың ұзындығы
 тоғыздықтан құралған сан
тоғыздықтан құралған сан
 -ге бөлінетіндей ең кіші
-ге бөлінетіндей ең кіші
 -ге тең. Ал периодтың өзі тоғыздықтардан құралған санның
-ге тең. Ал периодтың өзі тоғыздықтардан құралған санның
 -ге бөлгендегі
-ге бөлгендегі
 - таңбалы сан ретінде жазылған бөліндіге тең(басында нөлдері болуы мүмкін) . Салдар:
- таңбалы сан ретінде жазылған бөліндіге тең(басында нөлдері болуы мүмкін) . Салдар:
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz