Оқушыларды табиғаттағы тербелмелі және толқындық құбылыстарды меңгертуде жасалынатын физикалық практикумдар және оны ұйымдастырып өткізудің әдістері

Пән: Физика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 33 бет
Таңдаулыға:

Қазақстан Республикасының Білім және Ғылым министрлігі
М.Өтемісов атындағы Батыс Қазақстан мемлекеттік университеті

Физика және математика кафедрасы

КУРСТЫҚ ЖҰМЫС
Тақырыбы:

Оқушыларды табиғаттағы тербелмелі және толқындық құбылыстарды меңгертуде
жасалынатын физикалық практикумдар және оны ұйымдастырып өткізудің
әдістері

Орындаған:

Тексерген:

Орал – 2015ж.

Мазмұны

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ... ...3

1. ЭЛЕКТРОМАГНИТТІК ТОЛҚЫНДАР
1.1 Электромагниттік жарық шығарудың түйіршігі және
толқындық
қасиеттері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ..5
1.2 МОНОХРОМАТ ТОЛҚЫНДАР ЖӘНЕ ОЛАРДЫҢ ЭКСПЕРИМЕНТ ТҮРІНДЕ
ОРЫНДАЛУЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... 9

2. ОРТА БІЛІМ БЕРЕТІН МЕКТЕПТЕ ТЕРБЕЛІСТЕР БӨЛІМІ БОЙЫНША ЕСЕП ШЫҒАРУ
ӘДІСТЕМЕСІ
2.1. ОРТА БІЛІМ БЕРЕТІН МЕКТЕПТЕГІ ФИЗИКА КУРСЫНДАҒЫ ТЕРБЕЛІСТЕР БӨЛІМІНІҢ
ТЕОРИЯЛЫҚ НЕГІЗДЕРІ ... ... ... ... ... ... .. ... ... ... .12
2.2 МЕХАНИКАЛЫҚ ТЕРБЕЛІСТЕРГЕ БАЙЛАНЫСТЫ ЕСЕПТЕРДІ ШЫҒАРУ
ӘДІСТЕМЕСІ ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... 31

ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... .36
ПАЙДАЛАНЫЛҒАН
ӘДЕБИЕТТЕР ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... 37

КІРІСПЕ
Зерттеу өзектілігі. Қазіргі таңда білім беру жүйесін реформалаудың
маңызды бағыттары қатарынан білім сапасын көтеру мәселесі жетекші орын
алады. Жалпы білім беретін мектептерде білім сапасын арттыру, білім беру
мазмұнын жетілдіру, оқыту үрдісін жаңа сапалық денгейге көтеру
мұғалімдердің әдістемелік шеберліктерін арттыру сияқты факторлармен
байланысты.
Соңғы жылдарда педагогикалық процесті ізгілендіру тенденцияларын
күшейуі жаратылыстану пәндерін оқытуға аса көңіл бөлініп, болашақ ұрпақтың
техникалық білімдерінің терең болуын талап етіп отыр. Мектептерде арнайы
жабдықталған физикалық лабораториялар, жаңа буын оқулықтары т.б. оқыту
үрдісін жетілдіруге қажетті оқу-техникалық және әдістемелік құралдармен
қамтамасыз етуге үлкен қаржы бөлініп отыр.
Оқушыларға табиғаттағы тербелістер мен толқындық құбылыстарды меңгерту
еліміздің ғылым мен техниканың дамуы үшін үлкен маңызға ие. Себебі
тербелмелі қозғалыс - табиғат пен техникадағы ең көп тараған қозғалыс.
Тербеліс кездеспейтін салаларды айту қиын: ормандағы ағаштар да,
егістіктелі жайқалған бидай да, музыкалық аспаптардың шектері, машинаның
арқауы, ракете корпусы, іштен жану двигателінің поршені де тербелмелі
қозғалысқа түседі. Тербелмелі қозғалыстар біздің планетамыздың тіршілігінде
жер сілкіну, судың қайтуы мен тасуы, жүректің сорғуы, дыбыс желбезегінің
дірілі сияқты мысалдарда көруге болады.
Толқындық құбылыстар арасындағы тағайындалған тәуелділіктер физикалық
заңдылықтар болып табылады. Осы заңдылықтарды ашу нәтижесінде адамзат еңбек
құралдарынан бастап атом энергиясына дейін өзіне қызмет көрсететін дәрежеге
жетті.
Тербелістің адам өмірінде атқаратын маңызы зор. Тербеліс заңдарын
білмей радио, теледидар, қазіргі көптеген құрылғылар мен машиналарды жасай
алмаған болар едік.
Зерттеу жұмысында табиғатта және техникада өте маңызды болған
физиканың тербелістер мен толқындық құбылыстар теориясын практикада
қолдану, бөлім бойынша физикалық есептерді шығарудың әдістерін зерттеу және
есеп шығару барысында қолдану мәселесі қаралды.
Зерттеу жұмысының мақсаты. орта білім беретін мектепте оқушылардың
тербелістер жіне толқындық құбылыстар бөлімі бойынша физикалық есептерді
шығаруға әдістемелік-дайындау жүйесін жасау.
Зерттеу жұмысының міндеттері:
1. Тербелістер және толқындық құбылыстар бойынша оқушылардың біліміне
қойылатын талаптарды анықтау.
2 Тербелістер және толқындық құбылыстар бойынша оқушыларды есеп
шығаруға дайындық жүйесін жасау.
3. Бөлім бойынша есептер шығарудың алгоритмін жасау.
4. Тербелістер және толқындық құбылыстар бойынша жасалған жүйені
тәжірибелік эксперименттік тұрғыда сынау.
Зерттеу жұмысының құрылымы: кіріспеден, екі бөлімнен және қорытынды
мен пайдаланылған әдебиеттер тізімінен тұрады.
1. ЭЛЕКТРОМАГНИТТІК ТОЛҚЫНДАР
1.1 Электромагниттік жарық шығарудың түйіршігі және
толқындық қасиеттері
Жарықтың нақты табиғаты қандай – ол жарық көзі шығаратын
электормагниттік толқын ба немесе кеңістікке ұшатын, вакумда с жарық
жылдамдығымен таралатын, фотондар ағынын шығаратын, жарық көзі ме? Сырттай
қарағанда, жарықтың табиғатына мұндай екі түрлі көзқарас – толқындық
(электромагниттік) және кванттық (корпускулалық) бірін-бірі жоққа шығарады.
Толқындар мен бөлшектердің біраз белгілері бір-біріне қайшы. Мысалы,
қозғалыстағы фотон кеңістіктің бір нүктесінде бола алады, ал таралатын
толқынды кеңістікке жайылған деп қарау керек және оның кеңістіктің
белгілі бір нүктесінде болуы туралы айтуы мүмкін емес. Жарыққа осындай бір
жағынан толқындық қажеттілігі, жарықтың табиғаты туралы көзқарасымыздың
толық шешілмегендігі туралы ой салады. Кейде, барлық табиғаттағы әр түрлі
құбылыстарды жарықтың табиғатына байланысты не кванттық, не
толқындық көзқарас негізінде түсіндіруге болады деген ой да тууы мүмкін.
Оптиканың дамуы жарықтың табиғаты күрделі екі жақты екенін, оның
табиғаты толқындық және кванттық болатынын сондықтан оның бір толқындық
және кванттық қасиеттерін білінетінін керсетеді. Жарықтың екі жақтылық
қасиетін оның фотондардың негізгі сипаттамаларын беретін төмендегідей
өрнектерден көретіндігінен жақсы байқауға болады
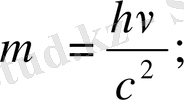
(1)
(1) өрнектерде фотонның корпускулалық сипаттамасы деп алатын үш
физикалық шамалар келтірілген. Фотонның осы үш кванттық сипаттамалары
жарықтың ең маңызды толқындық сипаттамасы 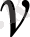жиілікпен тығыз байланыста
екеніне көңіл аударамыз.
Жарықтың қасиетінде байқалатын екі жақтылықта белгілі бір заңдылықтар
бар. Ұзын толқын сәуле шығаруда (мысалы, инфрақызыл жарықта) кванттық
қасиеттер өте аз білінеді, мұнда негізінен жарықтың толқындық қасиеті
басым. Оптикалық құбылыстардың үлкен бір тобы – интерференция, дифракция
және поляризация толығымен толқындық оптикамен түсіндіріледі. Алайда, егер
электромагниттік толқындар шкаласының бойымен солдан оңға қарай орын
ауыстырса, яғни ұзын толқындардан қысқа толқындарға қарай, онда жарықтың
кванттық қасиеті көбірек байқалады. Бұл әсіресе, фотоқұбылыстың қызыл
шекарасында және фотохимиялық реакциялар үшін осындай шекарасының
болатындығынан байқауға болады. Рентген сәулелерін қарастырғанда, оның
дифракциясын байқау үшін, қысқа толқынды рентген сәулелеріне кристалдық
торды пайдаланғанда ғана мүмкін болады. Осыған дейін рентген сәулелерінің
толқындық табиғаты белгісіз болса, енді оның да құпиясы ашылды.
Демек, жарықтың кванттық және толқындық қасиеттері бір-бірімен тығыз
байланыста. Осы байланыстылықты жарықтың мөлдір емес экранның саңылауынан
өту мысалы (1-сурет).

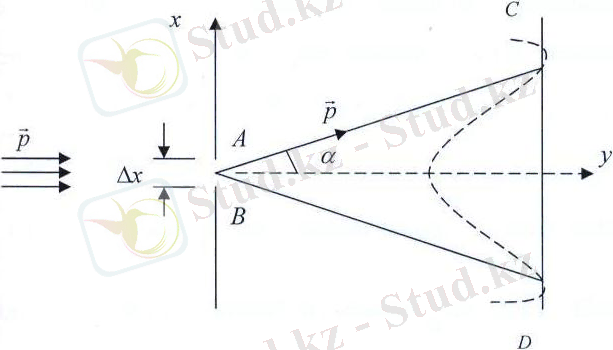
1 - сурет Экран бойынша жарықтың интенсивтілігінің таралуы
Айталық, жарық монохраматтық параллель сәулелер шоғы у өсінің бойымен
АВ саңылау арқылы өтсін. Бұл жарықтың екі жақтылық табиғаты туралы
көзқарасқа сәйкес, саңылау арқылы бір мезгілде бөлшектер жиыны – фотондар
және электромагниттік толқындар өтеді деген сөз. Белгілі, саңылаудан әрі
орналасқан СД экранында дифракциялық көрініс пайда болады. Экранның әр
нүктесінде жарық интенсивтілігіне пропорционал белгілі бір Е жарықтануы
байқалады, 1-суретте экран бойынша жарықтың интенсивтілінің таралуы
келтірілген. Мұнда жарықтың интенсивтілігі амплитуда квадратына
пропорционал екенін еске түсірсек жетіп жатыр. Демек экранның әр
нүктесіндегі амплитудасының квадратына пропорционал, яғни Е ~ А2. Кванттық
көзқарас бойынша, экрандағы дифракциялық көріністің пайда болуы, жарық
саңылау арқылы өткенде, кеңістікте фотондардың қайтадан бөлінуі жүреді де,
соның нәтижесінде экранның әр нүктелеріне саны әр түрлі фотондар келіп
түседі. Экранның берілген нүктесіндегі Е жарыктануы сол нүктеге уақыт
бірлігі ішінде жеткен фотондардың энергиясына байланысты. Демек, бұл
энергияны жеткізген фотондар саны -ге пропорционал. Олай болса .
Жоғарыда жарықтану үшін алынған екі өрнекті салыстырайық. Олардан
шығатыны 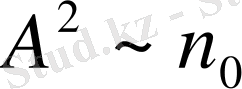. Кеңістіктегі кез келген нүктедегі жарық толқынының
амплитудасының квадраты, осы нүктеге келіп түсетін фотондар санына
пропорционал. Басқаша айтқанда, кеңістіктің берілген нүктесіндегі жарық
толқынының амплитудасы квадраты осы нүктеге фотондардың келіп түсу
ықтималдығының өлшемі болады. Сонымен, жарықтың толқындық және кванттық
қасиеттері бірін-бірі жоққа шығармайды, қайта олар бірін-бірі толықтыра
түседі. Бұл екі қасиет жарықтың затпен әсерлесуін және таралуының нақты
заңдылықтарын береді. Жарықтың кванттық қасиеттері, жарықтың энергиясы,
импульсі және массасы оның бөлшектерінде – фотондарда жинақталатынын
білдіреді. Фотондардың кеңістіктің әр түрлі нүктесінде болу ықтималдылығы,
олардың толқындық сипатымен — жарық толқынының амплитудасымен анықталады.
Осы аталғандардан шығатыны, толқындық қасиет бір мезгілде ұшатын фотондар
жиынтығына ғана тән емес, ол әрбір фотонға тән қасиет. Фотонның толқындық
қасиеті, жарық саңылаудан өткеннен кейін (1-сурет) экранның дәл қай
нүктесіне барып түсетіндігін айту қиын болған кезде білінеді. Демек, жерде
тек әр фотонның осы, не басқа нүктеге барып түсу ықтималдылығы турала ғана
айтуға болады.
Жарық толқындық және кванттық қасиеттерінің арасындағы осындай
байланыстылықпен түсіндіруді Эйнштейн ұсынған болатын. Демек, бұл осы
заманғы физиканың дамуында аса маңызды роль атқарады.

Есеп шығару мысалдары

1. Ұзындығы 1 мм шыны пластинаға 500 штрих салынған. Осыған толқын
ұзындығы 5,9 10-7 м жарық түседі. Осы дифракциялық тордың әсерінен
пайда болатын спектрдің ең үлкен ретін табыңыз.
Берілгені: а = 1 мм; n = 500; = 5,910-7 м.
Табу керек:
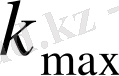
Шешімі: 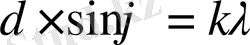формуласын пайдаланамыз, мұндағы 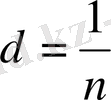болғандықтан,
теңдеу былай өзгереді: 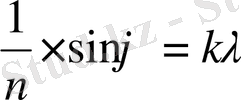. Спектрдің ең үлкен реті 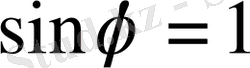болғанда пайда
болады. Демек,
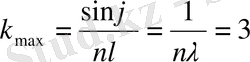
2. Дифракция көрінісінен Юнг тәжірибесінде саңылаулардың ара қашықтығы
d = 0,007 мм, ал қос саңылау мен экранның ара қашықтығы D = 2 м, аспапқа
жасыл жарық түсіргенде көршілес дифракциялық ашық жолақтардың ара қашықтығы
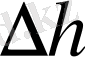= 16 мм болып шықты. Осы мәліметтер бойынша толқын ұзындығын анықтау
керек.
Берілгені: d = 0,007 мм; D = 2м; 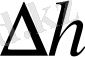= 16мм.
Табу керек: .
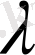Шешімі: Көршілес екі дифракциялық жолақтардың ара қашықтығы үшін
формуланы 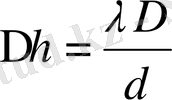қолдана отырып, келесі нәтижеге алынады:

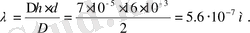
3. Дифракциялық тордың 1 мм-де 100 штрих бар. Дифракциялық тордың
периоды қандай?
Берілгені: а = 1 мм; n=100.
Табу керек: d.
Шешімі: Дифракциялық тордың периоды берілген а қашықтығында мына
қатынаспен анықталады:
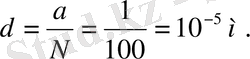
4. Жарықтың нүктелік көзі (= 600 нм) радиусы мм дөңгелек
саңылаулы диафрагма алдында орналасқан. Егер саңылау Френельдің бес зонасын
ашса және диафрагмадан бақылау нүктесіне дейінгі қашықтық 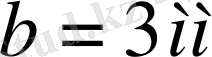болса,
көзден диафрагмаға дейінгі а қашықтығын анықтаңыз.
Берілгені: = 600 нм (610-7 м); = 2 мм (210-3 м);
;
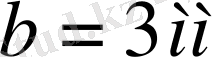т = 5.
Табу керек: а.
Шешімі: Френельдің m зоналары дөңгелек саңылау жазықтығының толқындық
бетінің ашық бөлігінде кемісін делік. Онда экрандағы бақылау нүкесінен
саңылау шетіне дейінгі қашықтық 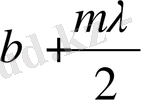болады (2-суретті қара).

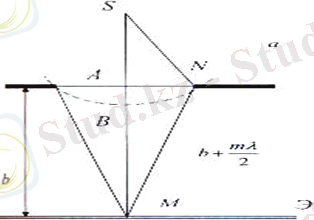
2 - сурет Френель зоналары
Пифагор теоремасы бойынша: 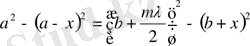мұндағы
х = АВ. 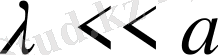және 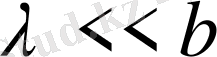екендігін ескерсек 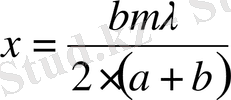өрнегін алынады (
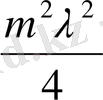бөлшегін ескермейміз). SAN үшбұрышын 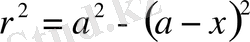өрнектегі х үшін есептелетін,
екінші ретті бөлшекті ескермей 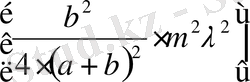көзден диафрагмаға дейінгі ара
қашықтықты алынады: 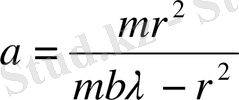=2,4 м.
6. Нүктелік жарық көзімен ( = 0,50 мкм) экран арасына радиусы r =
1 мм болатын дөңгелек тесігі бар диафрагма қойылған. Диафрагмадан жарық
көзіне және экранға дейінгі қашықтықтар R=1м, r=2м диафрагманы алып
тастағанда тесіктің ортасына сәйкес, Р нүктесінің жарықтануы қалай
өзгереді?
Берілгені: r = 1 мм (1-10-3 м); r0 =2м; R = 1м.
Табу керек: I.
Шешімі: экранның Р нүктесіндегі, жарықтану шамасы, яғни жарықтың
интенсивтілігі диафрагманың тесігіне сиятын Френель зоналарының санына
байланысты.
Егер зона саны жұп болса, Р нүктесіне қара дақ, ал зона саны тақ
болса, жарық дақ пайда болады. Сондықтан (1) өрнектІ пайдаланып, Рк шамасы
диафрагма тесігінің г радиусына тең екендігін ескеріп, зона санын табылады

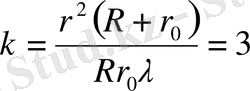
Демек, бұдан Р нүктесінде жарық дақ болатынын көреміз. Есепте қойылған
сұраққа жауап беру үшін мына жағдайларға тоқталамыз. Саңылауды шексіз
үлкейтсек (яғни бұл толқынның таралу жолынан диафрагманы алып тастау деген
сөз), онда барлық толқынның әсері. Френельдің бірінші зонасынан болатын
тербеліс амплитудасының жартысына тең болады 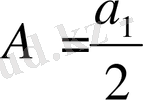. Демек, Р нүктесіндегі
жарықтың тербеліс амплитудасы екі есе азаяды. Ендеше I интенсивтілігі А
амплитудасының квадратына пропорционал 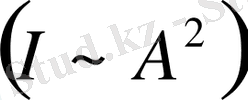, болғандықтан, Р нүктесіндегі
жарықтанудың шамасы 4 есе азаяды.

1.2 МОНОХРОМАТ ТОЛҚЫНДАР ЖӘНЕ ОЛАРДЫҢ ЭКСПЕРИМЕНТ ТҮРІНДЕ ОРЫНДАЛУЫ

1-зертханалық жұмыс
Малюс заңының зертелуі және фазалық пластина арқылы поляризациялық жарықтың
өтуі
Жұмыстың мақсаты: Малюс заңын тексеру және фазалық пластина арқылы өтетін
полярланған жарыққа талдау жасау.
Құрал-жабдықтар: РМС-З құрылғысы.
Теориялық мәлімет
Жарықтың электромагниттік теориясы бойынша, жарық толқыны көлденең,
яғни вектор болып табылады: Электр өрісінің кернеуі , магниттік
өрістің кернеуі және толқындық вектор 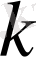өзара перпендикуляр.
Қарапайым көздерден шығатын жарықта көптеген толқын иірімдерінен тұрады,
онда жарық толқыны көлденең жарыққа бағытталады. Мұндай жарық табиғи
немесе поляризацияланбаған деп аталады.
Жарық векторы тербелістерінің бағыты қалай да тәртіппен
бағытталса, онда мұндай жарық поляризацияланған деп аталады.
Поляризацияланған жарықты алатын процесс поляризация деп аталады. Егер
вектор тербелісі бір жазықтықта пайда болса онда жарық жазық
поляризацияланған (немесе сызықты поляризазияланған) деп есептеледі.
Жарықтың вектор тербелісінің Е, өз бағыты болса бөліктенген поляризация деп
атайды. Вектор кернеулігі электр өрісіндегі және толқындық вектор k
жазықтықта жатса тербеліс жазықтығы немесе поляризация жазықтығы деп
аталады. Жарық поляризациясы жарық шағылғанда, сынғанда және анизотропты
заттар арқылы өткенде байқалады. Поляризацияланған жарықты алатын кез-
келген құрылғы физикалық эффектке тәуелсіз поляризациялатқыш деп аталады.
Визуалды поляризацияланған жарықты, поляризацияланбаған жарықтан
айыруға болмайды Поляризацияланған жазықтықты зерттеу анализатор деп
аталатын құрылғы арқылы жүзеге асырылады.

Жарықтың эллипстік поляризациясы

Поляризацияланған сәулелену ортақ жағдайда элиптік поляризациядан
тұрады. Осыған байланысты жарық толқынының Е ортогоналды компоненттері
алынған координаттар жүйесінде ( Z осі жарық таралуына параллель ) теңдеу
мына түрде жазылады:
(2)
(3)
Тербелістердің ортогоналдық түрлерін (2) және (3) қоссақ, XY
жазықтығында эллипстің проекциялық бейнесін береді. Эллипс формасы
параметрлермен анықталады:
-фаза айырмашылығы (4)
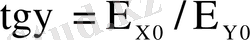-амплитуда қатынасы
(5)
Мұндай терминалогия толық қабылданбаған. Кейбір оқулықтарда
поляризацияланған жазықтық деп, магниттік векторы В (яғни вектор тербелісі
Е жазықтыққа перпендикуляр) бар жазықтықты айтады. Егер , π нолге тең
болса, эллипс түзу түрінде туады және сызықты поляризацияланған жарық пайда
болады. Егер δ=π2 және толқын жиынының амплитудасы тең болса, эллипс
шеңберге айналады- яғни шеңбер бойымен поляризацияланған жарық пайда
болады.
Е векторы айналу бағытына байланысты эллиптік поляризацияның оң және
теріс екенін айырады.Оң бұранда ережесімен айналса поляризация оң деп
аталады, қарама – қарсы жағдайда - теріс болады. Эллипс формасын түсіндіру
үшін, геометриялық интерпретацияға ие бола алатын басқа параметрлерді
қолдануға болады (3-сурет). χ - азимут таңдап алынған координат жүйесіндегі
эллипстік үлкен жартылай остегі ориентациясы.
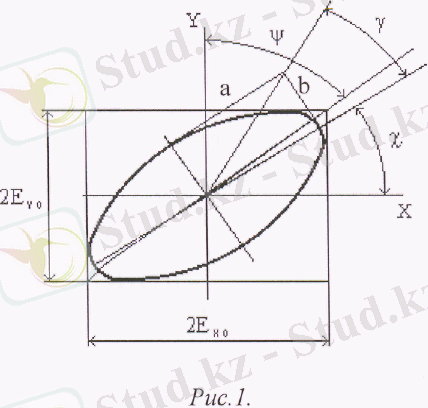tgγ = bа – эллиптілік жартылай остегі эллипс теңдеуінен таңдап
алынған жарты ості эллипс
3 – сурет. Е векторында айналу бағыты
ψ, δ жәнеχ, γ параметрлер арасындағы байланыс мынадай формулалармен
беріледі:
(6)
(7)
(8)
(9)
Екі жұп параметрлерінің және олардың арасындағы қатыс маңызды
практикалық мәні эллипстік поляризациясының көрінісін береді. Параметрлер
арқылы өлшенетін көптеген өлшенетін схема шамалары. χ және γ, интерпретация
өлшеу нәтижесінде, ал физикалық интерпретацияның нәтижесінде ψ және δ
параметрлері неғұрлым ыңғайлы (мысалы, өлшеу нәтижелерін өңдеу үшін
обьектің математикалық моделін Френель заңдарымен формулаларын қолдану
арқылы жүзеге асырады).

2. ОРТА БІЛІМ БЕРЕТІН МЕКТЕПТЕ ТЕРБЕЛІСТЕР БӨЛІМІ БОЙЫНША ЕСЕП ШЫҒАРУ
ӘДІСТЕМЕСІ
2.1. ОРТА БІЛІМ БЕРЕТІН МЕКТЕПТЕГІ ФИЗИКА КУРСЫНДАҒЫ ТЕРБЕЛІСТЕР БӨЛІМІНІҢ
ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

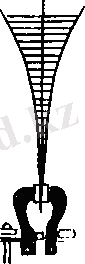
Тербеліп тұрған дене басқа денелермен байланыста болып, денелер
жүйесін құрады да, тербелмелі жүйе деген атқа ие болады. 1- суретте
тербеліс жасап тұрған механикалық құрылғылардың мысалдары келтірілген. Жер,
штатив, серіппе және жүк вертикаль серіппелі маятник құрады (1, а-сурет).
Суретте Жер көрсетілмеген. Жер, тіреу және жеңіл мықты жіпке ілінген
шар тербелмелі жүйе құрады да, оны физикалық маятник не жай ғана маятник
деп атайды (1, б-сурет). Екі штатив, екі серіппе және массасы m дене
тербелмелі жүйе құрады, оны әдетте горизонталь серіппелі маятник деп атайды
(1, в-сурет).
Барлық тербелмелі жүйеге тән ортақ қасиеттер болады. Солардың ең
бастыларын қарастырайық:
а) әрбір тербелмелі жүйенің орнықтылық тепе-теңдік күйлері болады.
Ілулі тұрған шардың массасының центрі ілу нүктесімен бір вертикаль бойында
жататын болса, онда математикалық маятник орнықтылық тепе-теңдік күйде
болады. Вертикаль серіппелі маятник осы күйде болу үшін ауырлық күші
серіппенің серпінділік күшімен теңгеріліп тұрады. Ал горизонталь серіппелі
маятник осы күйде болу үшін екі серіппе бірдей деформацияланған болу керек.
б) тербелмелі жүйе орнықтылық тепе-теңдік күйінен шығарылғаннан кейін
оны орнықтылық күйге қайтаратын күш пайда болады. Мұндай күштің шығу тегі
әртүрлі болуы мүмкін. Мысалы, физикалық маятник бұл ауырлық күші мен
жіптің 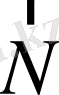реакция күшіне 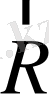тең әсерлі күші болса, 2-сурет, ал
серіппелі маятниктерде серпінділік күші болып есептеледі.
в) орнықтылық күйге қайтып келген тербелмелі жүйе бірден тоқтамайды.
Оған тербелген дененің инерттілігі кедергі болады.
Егер қандай да бір әдіспен тербелмелі жүйенің орнықтылық тепе-теңдік
күйін бұзсақ, онда сыртқы күштер болмаған жағдайда тербеліс пайда болады
да, біраз уақыт сақталып қалатынын жоғарыда келтірілген қасиеттер көрсетіп
береді.

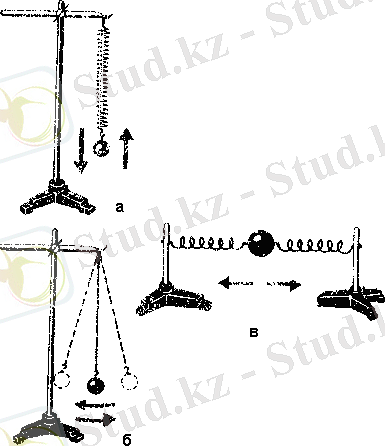
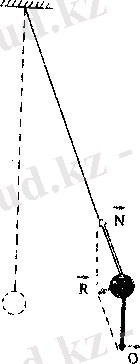
1-сурет
2-сурет

Еркін тербелістер
Егер тербелмелі жүйенің орнықты тепе-теңдік күйінен қандай да бір
ауытқуы сыртқы айнымалы әсерге соқтырмайтын болса, тербелмелі жүйеде пайда
болатын тербелістерді еркін немесе меншікті деп атайды.
3-сурет
Серіппеге қосылған магниттің тербелісі (3-сурет), серіппеге ілінген
жүктің тербелісі , шекті тепе-теңдік күйінен шығарған тербелістер еркін
тербелістердің мысалы бола алады.
Тербелістердің осциллограммасы
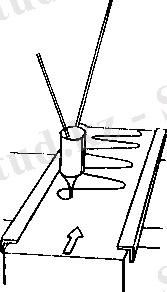
Егер маятникке сия құйсақ, маятник тербелгенде одан аққан сия
маятниктің ілу нүктесіне қатысты алғанда бір қалыпты қозғалып, қағазға
қисық сызады. (4-сурет). Қағаз жолақ бір қалыпты қозғалғандықтан, алынған
қисық уақыт өткен сайын маятниктің тепе-теңдік күйіне қатысты қалпынан
өзгергенін көрсетеді. Мұндай қисық осциллограммалар деп аталады.
Осциллограмма деген сөз латынның oscilum тербеліс және гректің графио
жазамын деген сөзінен шыққан.

4-сурет

Гармониялық тербелістер және оларды сипаттайтын шамалар

Табиғатта және техникада тербелістің сан алуан түрі кездеседі. Біз
мәселені оңайлатып, массасы m денеден тұратын, ұзындығы дененің өлшемінен
анағұрлым ұзын берік жіпке ілінген идеал маятникті көз алдымызға
елестетейік. Денені материалық нүкте деп атауға болады. Сонымен қатар,
маятник тербелген кезде үйкеліс күші де, ауаның кедергі күші де әсер
етпейді дейік. Мұндай маятник математикалық маятник деп аталған. әрине,
нақтысында математикалық маятник деген жоқ. Бірақ оның моделін жасауға
болады. Мысалы, ұзын, өте жеңіл, жіңішке, берік жіпке ілінген қорғасын не
болат шар математикалық маятниктің дөрекі моделі бола алады. Егер біз
ойлағандай математикалық маятник болса, оны тепе-теңдік қалпынан шығарып,
мыналарды анықтаған болар едік:
а) маятник шексіз тербеле береді (энергияның қайтымсыз түрленуі жоқ
боғандықтан);
б) оның тепе-теңдік қалпынан оңға ең үлкен ауытқуы солға ең үлкен
ауытқуына тең;
в) оңға ауытқу уақыты солға ауытқу уақытына тең;
г) тепе-теңдік қалпынан оңға және солға қозғалу сипаты бірдей.
Мұндай тербелістерді гармониялық деп атайды (гректің гармония -
үйлесімділік, келісушілік деген сөзі).
Кейінірек, біз гармониялық тербелістерді дәлірек анықтаймыз, ал әзірше
осы сипаттаумен шектелеміз.
Гармониялық тербелістерді сипаттайтын шамалар
Тербелстерді сипаттау үшін орын ауыстыру, жылдамдық және үдеуден басқа
қозғалыстың осы түріне арнаулы шамалар енгізілген. Осындай шамалардың бірі
ығысу болып табылады.
Ығысу деп тербеліп тұрған дененің тепе-теңдік жағдайынан орын
ауыстыруының ОХ осіне түсірілген проекциясын атайды (5- сурет). Ығысу –
скаляр шама.
Тербелмелі қозғалыста ығысудың мәні үздіксіз өзгеріп тұрады. Ығысудың
ең үлкен мәнін амплитудалық мән немесе амплитуда деп атайды. Амплитуданы Хm
деп бас әріппен белгілейді, ал кез келген уақыт мезетіндегі ығысуды х-пен
белгілейді.
Тербелмелі жүйенің толық бір тербелуге кеткен ең аз уақыт аралығын
период деп атайды. Период Т әрпімен белгіленеді.
Егер t уақыт ішінде N толық тербеліс жасалған болса, онда тербеліс
периоды былай анықталады:

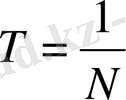
Сонымен, тербеліс периоды деп толық бір тербелуге кеткен уақытты
атайды.
Дененің 1 секунд ішінде жасаған тербеліс санын тербеліс жиілігі деп
атайды. Әдетте тербеліс жиілігін ν әрпімен белгілейді. Егер t уақыт ішінде
толық N тербеліс жасалған болса, онда

Жиілік деп 1 с ішінде жасалған толық тербеліс санын айтады. Жиіліктің
бірлігі ретінде 1 секундта бір тербеліс жасайтын жиілікті алады. Жиіліктің
осы бірлігін Г е р ц (Гц) деп атайды. Бұл бірлік неміс физигі Генрих
Герцтің құрметіне берілген. Практикада іс жүзінде жиілікті өлшеу үшін
еселік бірліктер килогерц (кГц), мегагерц (МГц) және гегагерц (гГц)
пайдаланылады.
Период пен жиілік формулаларын салыстыра отырып, бұлардың бір-біріне
кері шама екенін көреміз.
Гармониялық тербелістердің динамикасы
Тербелмелі жүйелердегі еркін тербелістің динамикасын үйкеліс жоқ идеал
тербелмелі жүйелерде қарастырайық.
Серіппелі маятниктің шарын тепе-теңдік қалпынан аз ғана қашықтыққа
ауытқытайық. Бұл жағдайда серіппе деформациясы серпінді болсын (5-сурет).
Бұл жағдайда шарға тепе-теңдік қалпына қарай бағытталған қайтарушы күш әсер
етеді. Бұл күш (Гук заңы бойынша) тепе-теңдік қалпынан ауытқыған дененің
ығысуына пропорционал:
F=-k x.
Қайтарушы күш тепе-теңдік қалпына қарай бағытталған, ал оның
проекциясының таңбасы әруақытта х ығысуының таңбасына қарама-қарсы болады.

5- сурет
Математикалық маятник жағдайында да осылайша болады. Маятникті тепе-
теңдік қалпынан шамалы қашықтыққа ауытқытамыз (2- суретті қараңдар). Бұл
жағдайда ауырлық күші мен жүктің серпінділік күшінің тең әсерлі күші тепе-
теңдік қалпына қарай бағытталады. Бұл күшті былайша өрнектеуге болады:

F=mgsinα.
Біз ауытқу бұрышы аз болатын тербелістерді ғана зерттейміз. Бұл
жағдайда sinα. Сондықтан F== шамасы тұрақты. Оны k
деп белгілейміз. Сонда F=-kx. Күш ығысуға қарама-қарсы жаққа қарай
бағытталған.
Сонымен, серіппелі және физикалық маятниктерді тербеліске түсіретін
күштердің табиғаты әр түрлі (ауырлық күші және серпінділік күші)
болғанымен, ығысуды қайтарушы күштің тәуелділігі бірдей: қайтарушы күш
тербелістегі дененің тепе-теңдік қалпынан ауытқығандағы ығысуына
пропорционал және әр уақытта тепе-теңдік жағына қарай бағытталады. Бұл
гармониялық тербелістерге тән қасиеттердің бірі
Гармониялық тербелістердің кинематикасы
Маятник тербелісінің осциллограммасы мынаны көрсетеді: егер үйкеліс
күші жоқ болса, маятниктің амплитудасы тұрақты қалып, ал ығысуы синусоида
заңымен өзгерер еді. Бұл ұйғарымның дұрыстығы маятник тербелген жағдайда
қайтарушы күш синусоидасы өзгеруінен дәлелденеді: F=mgsinα. Демек, осы
күшпен маятникке берілген үдеу де синусоидалы өзгереді: .
Тербелістердегі энергия айналуы. Еркін ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.