Симплекс әдісі және оның қолданылу алгоритмі

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ...3-4
І. Симплекс әдісі және оның қолданылу алгоритмі
1.1. Симплекс әдістің
теориясы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ..5-8
1.2. Симплекс әдісі туралы
түсінік ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 9-
12
1.3. Симплекс әдісі
алгоритмі ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ..13-14
ІІ. Симплекс әдісімен есеп шығару
2.1. Симплекс әдісін пайдаланып есеп шығару
үлгілері ... ... ... ... ... ... ... ...15-22
2.2. Жасанды базистің симплекс
әдісі ... ... ... ... ... ... ... .. ... ... ... ... ... ... ..23-28
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... .29-30
Пайдаланылған әдебиеттер
тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ...31-
32

Кіріспе
Математикалық ықшамдауда, Данцигтің симлекс алгоритмі (немесе
симлекстік әдіс) сызықтық программалауда кеңінен таралған алгоритм.
Информатика төңiрегiндегi техникалық есептеуiш журналы (The journal
Computing in Science and Engineering) бұл алгоритмді 20 ғасырдың он мықты
алгоритмдерінің біреуіне жатқызды. Алгоритм аты Т.С.Мотцин айтып кеткендей
жеңіл (simplex ) деген сөзден шыққан. Симплекс әдістерде қолданыс таппайды,
бірақ ол симплексациялық конустарға ісерін тигізеді, қосымша шектеулермен
симплекстерге тиісті болады.
К. Маркстің Ғылым математиканы пайдалануға мүмкіндігі болса
кемелдікке жетеді - деген тезисінің әділдігі күннен-күнге дәлелдене
түсуде. Математикалың әдістер мен компьютерлік технологиялар нарықтың даму
жағдайында жоспарлау мен жедел басқару мақсаттары үшін экономикалық
зерттеулердің күнделікті әрекетіне ойдағыдай кірігуі - бүгінгі күн
тіршілігінің шынайы көрінісі.
Қазақстанда жүргізлеетін макроэкономикалық саясатты, белең алған
макро-микроэкономикалық үдерістердің теориялық мәнін түсіну және сонымен
бірге математикалық, ақпараттың модельдеу тұтастай білім беру бағытында да
(жоғары оқу орындарында), сонымен бірге экономистердің айтарлықтай бөлігін
арнайы даярлауды сөзсіз қажет етеді.
Президент Н.Ә. Назарбаев Л.Н. Гумилев атындағы Еуразия ұлттық
университетіндегі өз лекциясында: Талдаудың математикалық әдісттрін
инженерлер, экономистер, заңгерлер, құрылысшылар, мемлекет қайраткерлерінің
барлығы да игеруге тиіс деп ерекше атап өтті.
Қазіргі таңда математикалық әдістер қайсыбір дәрежеде пайдаланылмайтын
адамзат тіршілігінің саласын табу қиын. Экономикалық қызмет те осыны
дәлелдейді. Алайда осы күнге дейін экономикалық үдерістерді модельдеу
саласында айтарлықтай табысқа жету байқалмайды.
Біздің ойымызша, осы жағдайды төмендегі себептермен түсіндіруге
болады:
Экономикалық үдерістер әжептәуір шамада ретсіз, басқарусыз өрбиді. Олар
саяси, мемлекеттік және жекелеген салалардың шаруашылық басшыларының
тарапынан ел экономикасын тұтастай жігерлі басқару әрекетіне бағынбайды.
Осы себептен экономикалық жүйелер нашар зерттеліп, формалы түрде
сипатталған.
Экономика саласы мамандарының, әдетте, математикалық
жалпы, атап айтқанда, математикалақ модельдеу мәселелері бойынша даярлығы
нашар. Олардың басым көпшілігі қадағаланатын экономикалық
үдерістерді нысандандырылған түрде сипаттай (нысан құра) алмайды. Осының
салдарынан қарастыратын экономикалық жүйе сол немесе басқа математикалық
моделъдің сәйкестігін анықтауға мүмкіндік бермейді.
Математикалық модельдеу саласындағы мамандардың қолында экономикалық
үдерістің нысандандырылған сипаты болмағандықтан олар оған сәйкес
математикалық модель құра алмайды.

І. Симплекс әдісі және оның қолданылу алгоритмі
1.1. Симплекс әдістің теориясы
АҚШ- та сызықты программалау 1947 жылдан бастап, Дж Данциг -–
еңбектерінде қалыптаса бастады. Ол, кейін симплекс әдіс деген атақ алған
сызықты программалау есептерін шығарудың қолдануға жеңіл, сандық әдісін
ойлап тапты.
Қойылған кедергілерге қарамастан Л.В. Канторович та экономикалық
идеяларға құрылған математикалық жұмыстарына қайта оралып, Д.Ж.Данцигтен
тәуелсіз симплекс әдістің идеясына келді. Оның бұл еңбектерін жоғары
бағалаған Д.Ж.Данциг Канторович өндіріске қатысты есептердің үлкен ,
маңызды класын математикалық тұрғыдан сипаттауға көз жеткізген бірінші адам
болды. Оның ойынша бұлай сипаттау есепке сандық тұрғыдан қарауға және оны
сандық әдістермен шығаруға мүмкіндік береді...Канторович алғашқы табылған
мүмкін шешімді пайдалануға негізделген әдісті сипаттады... -деп, өзінің
сызықты программалаудың тарихына арналған еңбегінде атап өтті.
Симплекс - әдістің алгоритмі қадамдарын тізбекпен реттеп жазайық та,
оның есептелу жолын мысалмен көрсетейік. Бұл тура симплекс - әдіс деп
аталады. Сонымен, алгоритм мынадай қадамдардан тұрады:
Қадам 0. Бастапқы базисті шешімді таңдау және алғашқы симплекс-кестені
толтыру (бір рет орындалады).
Қадам 1. Ағымдағы шешімді тиімділікке тексеру. Егер шешім тиімді
болса, онда есептеуді аяқтаймыз, әйтпесе келесі қадамға көшеміз:
Қадам 2. Шешімді жетілдіру бағытын таңдау және параметрлерін анықтау.
Қадам 3. Жаңа жетілген(лучшему) шешімге көшу. Қадам 1-ге қайта
оралу.
Өнім шығаруды жоспарлау есебін симплекс-әдіспен шығару жолын,
келтірілген алгоритмдерді пайдаланып шығарайық.
Теңдеу- шектеулермен берілген СПЕ қойылсын.
Қадам 0. Бастапқы базисті шешімді таңдау.
Базисті айнымалылар үшін қосымша 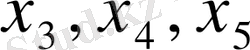– айнымалыларын таңдаймыз.
Сонда 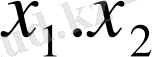- еркін айнымалылар болады да базисті шешім
Х0= (0,0,24,12,8) - түрінде болады.
Қосымша айнымалылардың экономикалық мағыналарына тоқталайық:
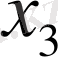- 1-ші түрлі шикізаттың қалдығы,
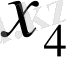- 2-ші, ал - 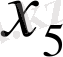3-ші түрлі шикізаттар қалдығы. О.б., бастапқы
шешімді былай түсіндіруге болады: егер ешқандай өнім шығармасақ 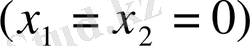, онда
шикізат қалдықтарының бәрі де қалдыққа көшеді 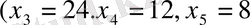. Бұл жағдайда табыс
түспейді, яғни
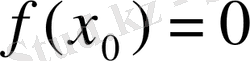
СПЕ-нің бастапқы мәліметтерін және бастапқы шешім туралы ақпараттарды
симплекс-кестеге енгіземіз (n-айнымалылар саны, m-шектеулер саны).

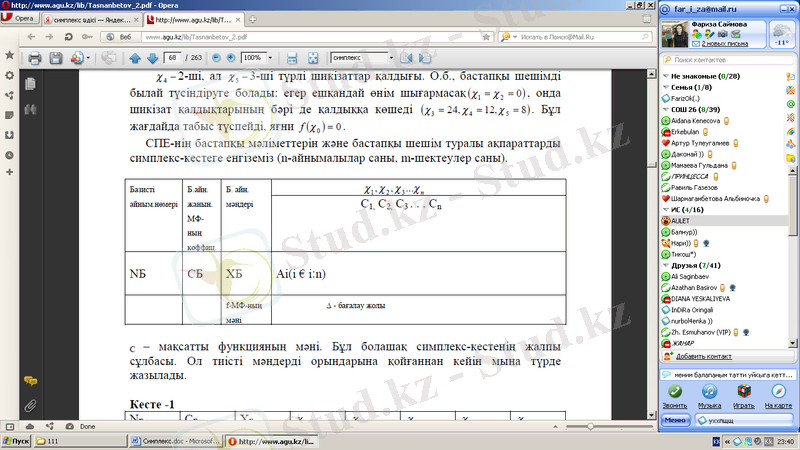
С – мақсатты функцияның мәні. Бұл болашақ симплекс-кестенің жалпы
сұлбасы. Ол тиісті мәндерді орындарына қойғаннан кейін мына түрде жазылады.

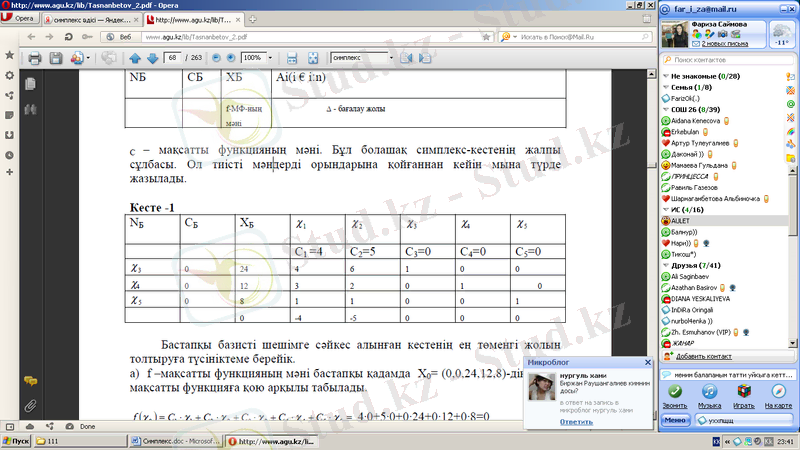
Бастапқы базисті шешімге сәйкес алынған кестенің ең төменгі жолын
толтыруға түсініктеме берейік.
а) f –мақсатты функцияның мәні бастапқы қадамда Х0= (0,0,24,12,8)-дің
мәнін мақсатты функцияға қою арқылы табылады.

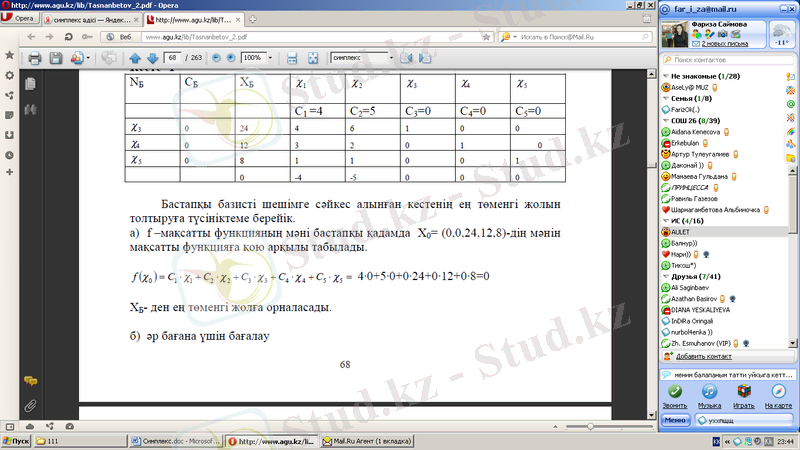
ХБ- ден ең төменгі жолға орналасады.
б) әр бағана үшін бағалау

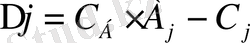
теңдігімен жүргізіледі. Бұл мәндер шешімдерді тиімділікке тексеретін
шамалар.Қалай есептелетіндігіне тоқталайық.
1) Δ1 –ді есептеу үшін

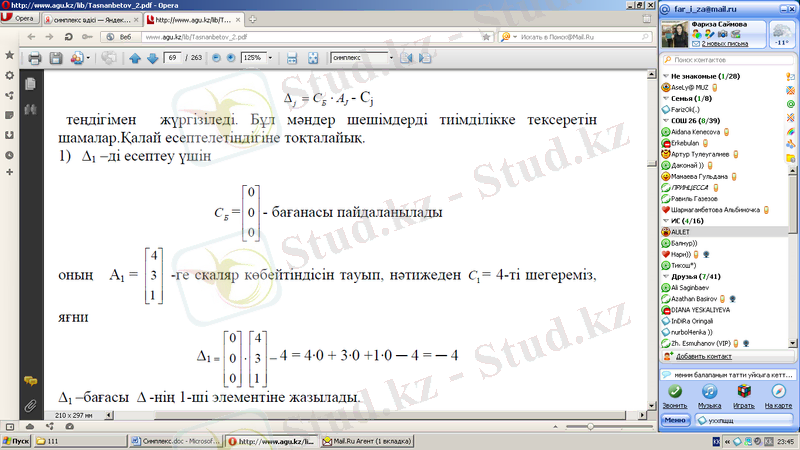- бағанасы пайдаланылады.
Оның 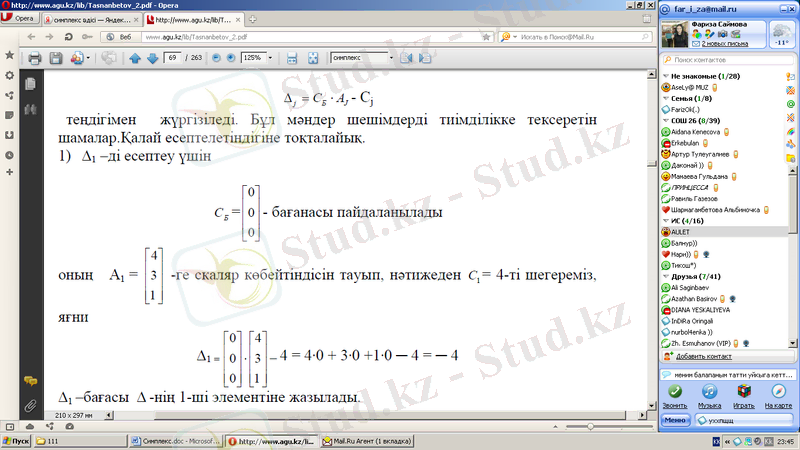-ге скаляр каляр көбейтіндісін тауып, нәтижеден 1 C = 4-ті
шегереміз,
яғни

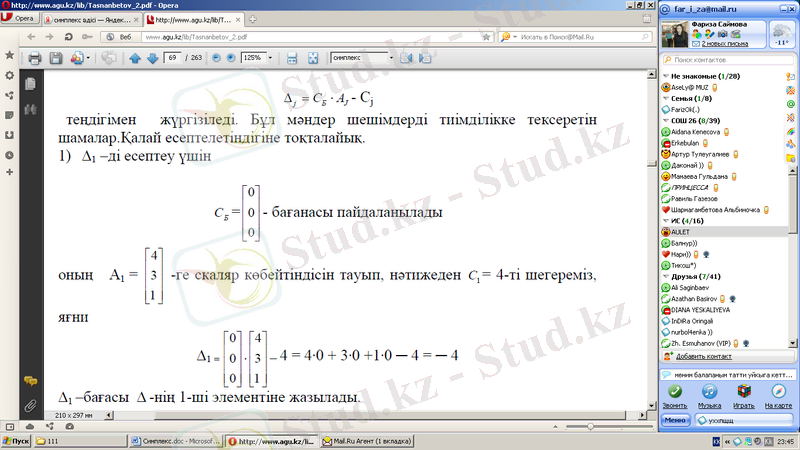
Δ1 –бағасы Δ -нің 1-ші элементіне жазылады.
2) Осылайша қалған бағалауларды да анықтаймыз.

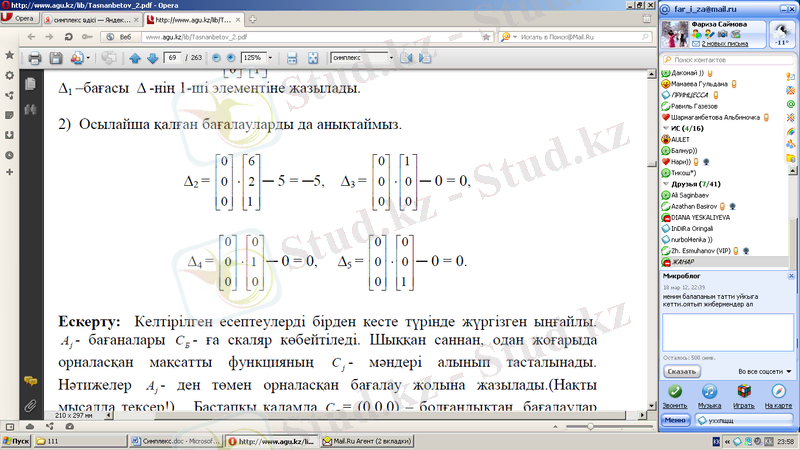
Ескерту: Келтірілген есептеулерді бірден кесте түрінде жүргізген
ыңғайлы.
A j - бағаналары C Б - ға скаляр көбейтіледі. Шыққан саннан, одан
жоғарыда орналасқан мақсатты функцияның С j - мәндері алынып тасталынады.
Нәтижелер A j - ден төмен орналасқан бағалау жолына жазылады.(Нақты
мысалда тексер!) Бастапқы қадамда C Б = (0,0,0) – болғандықтан, бағалаулар
теріс таңбасымен алынған мақсатты функцияның мәндеріне тең болып тұр.
Мақсатты функцияның мәндері мен бағалаулар тек бастапқы қадамда ғана
есептеледі. Қалған уақытта автоматты түрде саналады. Симплекс – кестені
толтырумен оның 0-ші немесе бастапқы қадамы аяқталады.
1.2. Симплекс әдісі туралы түсінік
Сызықтық бағдарлама есебінің оңтайлы шешімдері көпбұрыштың бұрыштық
нүетелерімен байланысты. Егер айнымалалар саны n=50,теңсіздіктер саны m=25
болса, онда базистік жоспарлар саны 1014 болады. Сонда м және н үлкен сан
болса, онда барлық негізге алынатын жоспарларды іріктей отырып, оңтайлыны
табу өте көп есептеуді қажет етеді. Сондықтан бір негізге алынатын
жоспардан екіншіге ауысуға мүмкіндік беретін әдіс болуға тиіс. Осындай әдіс
симплекс әдісі деп аталады. Есептеулердің әрқайсысында осы функцияның өткен
жоспардағы мәнімен салыстырғанда мақсатты функциядан кем немесе артық
мәніне сәйкес келетін жаңа жоспар табылды. Есептеулерді оңтайлы жоспар
алынғанға дейін жалғасады. Егер мәселенің оңтайлы шешімі болмаса, онда
симплексті әдіс оны есептеу кезеңінде анықтауға мүмкіндік береді.
Алғашқы жоспар құру. Сызықтық бағдарлама есебі қойылған болсын.
Төмендегі функцияның барынша аз мәнін табу қажет.

F=C1X1+ C2X2+... +CnXn (1)

мына шектеулерде

а11х1+ а21х2+... +а1nхn=В1
а21х1+ а22х2+... +а2nхn=В2 (2)
аm1х1+ аm2х2+... +аmnхn=Вm

мұнда,
хj=0, (i=1,2,...,m) (3)
Шектеу жүйесінің m бірлік векторлары болсын деп ұйғарсақ, онда ол
алғашқы m векторлар болады. Осыдан (1) – (3) есепті алғашқы m векторларға
сәйкес түрлендіріп жазамыз:

F=C1X1+ C2X2+... +CnXn (4)
мына шектеулерде

X1+a11,m+1Xm+1+a11,m+2Xm+2+...+a11.nx n=B11
X2+a2,m+1Xm+1+a2,m+2Xm+2+...+a12.nxn= B12 (5)
Xm+a1m,m+1Xm+1+a1m,m+2Xm+2+...+a1m.nx n=B1m

хj=0, j=1,2,...,n (6)

Жүйені (5,5) векторлық формада жазамыз:
x1A1+x2A2+...+xmAm+xm+1Am+1+xnAn=B (7)

А1, А2,...,Аm векторлар – m өлшемді кеңістіктің сызықтық тәуелсіз
бірлік векторлары. Сондықтан (7) өрнекте базистік айнымалылар ретінде
x1,x2,...,xm. Ал еркін айнымалылар ретінде xm+1,xm+2,...,xn таңдаймыз, оларды
нөлге теңестіріп, базистік айнымалыларды анықтаймыз. Мұнда ві=0 (і=1,2,...
m), ал А1, А2,..., Аm бірлік векторлар екенін ескерсек, онда алғашқы
жоспарды аламыз:
Хо=(х1=в1; х2=в2; ... хm=вm; хm+1=0; ... хn=0) (8)
Жоғарыдағы (7)-ден (8) жоспарды ескерсек, төмендегі жіктеу шығады:
x1А1+х2А2+... + хm,Аm = В,
(9)
мұнда А1, А2, ...А m векторлар сызықтық тәуелсіз, демек, құрылған
жоспар базис болып табылады.
1-анықтама. Еркін белгісіздердің нөл мағыналарына сәйкес келетін
шектеулер жүйесінің (2) шешімі базистік деп аталады.
Бастапқы негізге алынатын жоспарға (9) сүйене отырып, екінші негізге
алынатын жоспарды қалай құруға болатынын қарастырамыз. Базиске кірмейтін
кейбір вектор үшін, мысалы Аm+1, жіктеудегі хі,m+1 коэффициенттердің ең
болмағанда біреуі оң болады деп ұйғарамыз.
Х1,m+1А1+Х2,m+1А2+... + Хm,m+1Аm =Аm+1
Жүйенің оң жағы В бөлікті осы айнымалының оң коэффициенттеріне, яғни
Віаіm+1 бөлеміз. Сөйтіп, хm+1 векторы жоспар немесе жаңа базис болып
табылады. Есептің m-нен асатын базисі болмайды, сондықтан қазіргі бар
базистің біреуін алып тастаймыз. Ол үшін Q=min(віаi,m+1). таңдаймыз. Осы
ең кіші мәні бірінші жолда тұрсын, яғни Q1=min (віа1,m+1). Сонда жаңа
базистік шешім аламыз Х=( x2, хз,...хm,хm+1). Бұл базистен Х1 алып тастау,
ал базиске хm+1 енгізу қажет екенін білдіреді. Демек, негізге алынатын жаңа
жоспарларды таңдау үшін, базистен шығарылатын және оның орнына базиске
енгізілетін айнымалының векторын таңдау кажет.
Оңтайлылық талаптары. СБ есебінің базистік шешімі бар деп ұйғарамыз.
Бұл жағдайда есептің математикалық формасы төмендегідей болады:
x1 А1+х2А2+... + хmАm = В (10)
х1С1+х2С2+... + хmСm = Ғ (11)
мұнда барлық хj=0, j=1,2,...,n., ал Ғ-осы жоспарға сәйкес келетін
функцияның мәні. Егер сызықтык функциядағы Сj коэффициенті Аj векторға
сәйкес келсе, онда Ғj –Сj- оңтайлылық өлшемі немесе сызықтық функцияның
бағасы деп аталады.
Оңтайлылық өлшемі бағдарламадан шығарылатын қызметтің құнының сомасына
тең болады, одан жоспарға енгізілетін өнімнің бірлігінен түсетін кіріс
алынып тасталады. Ғj – мақсат функциясының коэффициенттерін шектеулердегі
айнымалылардың коэффициенттеріне көбейтіндісінің қосындысына, яғни,

cj – мақсат функциясының белгісіздер коэффициенттері. Төмендегі
теоремалар орын алады.
1-теорема. Егер кейбір Аj векторы үшін төмендегі талап орындалса,
Fj-Cj=0,
онда Хо жоспары функцияның максимумы үшін оңтайлы болып табылады.

2-теорема. Егер кейбір Аj векторы үшін төмендегі талап орындалса, онда
Хо жоспары функцияның минимумы үшін оңтайлы болып табылады. Демек, сызықтық
функцияның максимумына сәйкес есептің жоспары оңтайлы болу үшін оның
бағалары оң болуы қажетті әрі жеткілікті болады. Ал функцияның минимумы
үшін оның бағалары теріс болуы қажетті әрі жеткілікті болады.
Сөйтіп, мәселені симплекс әдіспен шешу мына сызба бойынша жүргізіледі:
1) базистік шешім құрылады;
2)осы базистік шешім оңтайлылық шартына тексеріледі;
3)егер шарт орындалмаса, онда келесі базистік шешім құрылады да екінші
тармаққа көшеді;
4)оңтайлылық талабы орындалғанға дейін есептеулер кайталанады.
Осы әдіспен есептеулер қайталана отырып, іріктеу нәтижесінде ең жақсы,
яғни оңтайлы шешім табуға болатыны дәлелденген.

1.3. Симплекс әдісі алгоритмі

Симплекс әдістің кестедегі алгоритмін қарастырайық. Есепті максимумға
қарастырамыз.
Симплекс-кесте
№ Базис Оң жағы, Айнымалылар Q
вi
x1 х2... хm хm+1 xm+2
... хп
1 xm+1 b1 a11 a12 a1m 1 0
...0
2 xm+2 b2 A21 a22 a2m 0 1...0
... ... ... ... ... ... ... ... ...
m xm+n bm Am1 am2 a1m 0 ... ...0
m+1 Fj-Cj 0 c1 c2 cm 0 0 ... 0

1. Алғашқы базистік жоспарды құру.
Симплекс әдіспен шешілетін есептің шектеулер жүйесі = таңбасымен
теңсіздіктер жүйесінде берілген, оның оң жағы bi=0. Теңсіздіктер жүйесіне
оң қосымша айнымалылар енгізу арқылы теңдеулер жүйесіне көшеміз. Осы
айнымалылардың баған векторлары бірлік векторлар болып табылады және базис
құрайды, сонымен бірге оларға сәйкес келетін айнымалылар базистік деп
аталады:
Мұнда хn+I - базистік айнымалылар, хj- еркін айнымалылар.
Енді симплекс әдісінің орындалу ретін(алгоритмін) кестеде
қарастырайық.
1)Симплекс кесте құрамыз. Кесте шектеулер жүйесі коэффициенттерінен
және оң жағынан тұрады. Кестенің соңғы жолы индекстік деп аталады және
мақсат функциясының қарама – қарсы таңбаларымен алынған коэффициенттерімен
толтырылады.
2) Оңтайлылықты тексеру. Индекстік жолда теріс санның бар-жоғын
анықтаймыз. Егер теріс сан болмаса, онда табылған негізге алынатын жоспар
функцияның максимумына сәйкес оңтайлы шешімі болып табылады. Егер индекстік
жолда теріс сандар болса, онда осы кестедегі айнымалылар есептің оңтайлы
шешімі емес немесе алгоритмнің келесі кезеңіне көшеміз.
3)Бағыттаушы баған мен жолды анықтау. Бағыттаушы баған мен жолды
табамыз. Бағыттаушы баған индекстік жолдың теріс санының барынша көп
абсолюттік мөлшері бойынша, ал бағыттаушы жол – бос мүшелер векторы
бағанының элементтерін бағыттаушы бағанның оң элементтеріне
min(biair) қатынастарының барынша аз абсолюттік мөлшерімен анықталады.
Бағыттаушы баған мен жол түйіскен жерде бас элемент орналасқан.
4)Жаңа негізге алынатын жоспар кұру. Бағыт беруші жол мен бағанға
сәйкес келетін белгісіз айнымалылардың орны ауыстырылады. Мұнда базистік
айнымалы еркін айнымалы болады және керісінше. і жолда және j бағанда
орналасқан элементтің (Эн ) жаңа мәні элементтің (Эс ) ескі мәнінен j баған
мен бағыттаушы жол (Э1) түйіскен жерде орналасқан Элементті і жол мен
бағыттаушы баған түйіскен жерде орналасқан элементке (Э2) көбейтіп, бас
элементке (Эг) бөліп алып тастағанға тең болады. Бұл тікбұрыш ережесі деп
аталады:
Эн=Эс-
5)Немесе төмендегі формулалар бойынша:
В1= (ві-(вгаrk)аіk болса і r ; brаrk болса і=r)
(12)
а'ij= (аij-аrjark)аіk болса і=r ; аrjаrk болса і=r)
(13)
Ғ'о=Ғо- (bгrаrk) k; j=А,- (аrіаrk) k
(14)
Барлық осы сандар жаңа симплекс кестеде жазылады.
6)Табылған жаңа базистің оңтайлылығын тексеру. Егер жоспар оңтайлы
болмай, жаңа оңтайлы жоспарға көшу қажет болса, онда 4) кезеңге қайта
оралады, ал оңтайлы жоспар алынған жағдайда, есептің шешімі қабылданады.

ІІ. Симплекс әдісімен есеп шығару
2.1. Симплекс әдісін пайдаланып есеп шығару үлгілері
Симплекстік әдіс сызықтық бағдарламалау есептерін шешудің әмбебап
әдісі болып табылады. Сызықтық бағдарламау есебін карастырайық.
Есеп. Еңбек ресурстарының мына мөлшері, яғни 2700 адам күн, 1200 га
мөлшеріндегі минералды тыңайтқыш және осы дақылдарға арналған 580 га
егістігі бар ауыл шаруашылығы кәсіпорнының бөлімшесіндегі дәнді дақыл, қант
қызылшасы мен күнбағыс егістіктерінің көлемін анықтау қажет.
Есептің мақсаты. Дәнді дақылдардың, қант қызылшасының және күнбағыс
егістіктерінің қандай үйлесімі фермерге пайда әкелетінін анықтау қажет.
Есептің шешуі. Бастапқы деректер 1-кестеде келтірілген.
1-кесте
Ауыл шаруашылығы Еңбек шығындары, 1 га-дан түсетін пайда,
дақылдары адам-күн тыңайтқыш ц. а.б
Дәнді дақылдар 1 1,7 200
20 4 350
Қызылша 0,9 1,6 300
Күнбағыс

Есептің шешімі экономикалық – математикалық модельді құрудан
басталады. Бұл үшін экономикалық терминдерде қалыптастырылған есептің
шартын математикалық формада жазамыз.
Төмендегі белгілерді енгіземіз:
Х1-дәнді дақылға бөленген егістік көлемі, га
Х2-қызылшаға бөлінген егістік көлемі, га
Х3-күнбағысқа бөлінген егістік көлемі, га
Шектеулер жүйесі шартқа негізделіп жазылады, оған сәйкес ресурстардың
әрбір түрі бойынша шығындар осы ресурстардың қолда бар қорынан аспауға
тиіс.

Мақсат функциясы ауыл шаруашылығы дақылдарын сатудан түсетін жалпы
пайданың максимумы болып табылады.

Zmin=200Х1+350Х2+300Х3, (16)

сондай-ақ мәселенің экономикалық мағынасынан олардың айнымалылардың
теріс емес шарты керсетіледі, яғни,

Х,0, Х20, Х3
(17)
Шектеулер жүйесіне (15)-(17) теріс емес қосымша айнымалылар
енгізе отырып, канондық түрге айналдырамыз

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.