Шартты экстремумдар және Лагранж көбейткіштері әдісі: теория және есептік мысалдар


Шартты экстремум.
z=f(x; y) функциясын х және у айнымалылары
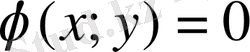 теңдеуімен байланысты болған жағдайда экстремумге зерттеу керек болсын. Яғни, z=f(x; y) функциясынан басқа ХоУ жазықтығында α сызығы беріліп, z функциясын экстремальдік нүктелері тек α сызығына тиісті болуы мүмкін жағдайда экстремумге зерттеу керек. Бұл нүктелер шартты экстремум нүктелері, ал х және у айнымалыларын байланыстыратын теңдеу - байланыс теңдеуі деп аталады.
теңдеуімен байланысты болған жағдайда экстремумге зерттеу керек болсын. Яғни, z=f(x; y) функциясынан басқа ХоУ жазықтығында α сызығы беріліп, z функциясын экстремальдік нүктелері тек α сызығына тиісті болуы мүмкін жағдайда экстремумге зерттеу керек. Бұл нүктелер шартты экстремум нүктелері, ал х және у айнымалыларын байланыстыратын теңдеу - байланыс теңдеуі деп аталады.
Егер
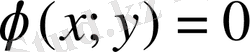 байланыс теңдеуінінен у айнымалысын х арқылы анықтап берілген z=f(x; y) функциясына қойсақ, онда бір х айнымалысынан тұратын функциясына келеміз. х-тің z функциясы экстремумге жететін мәндерін тауып байланыс теңдеуіне қоямыз да, у-тің сәйкес мәндерін анықтаймыз. Нәтижесінде шартты нүктелерін алмасақ, онда Лагранж көбейткіштері әдісін қолданамыз.
байланыс теңдеуінінен у айнымалысын х арқылы анықтап берілген z=f(x; y) функциясына қойсақ, онда бір х айнымалысынан тұратын функциясына келеміз. х-тің z функциясы экстремумге жететін мәндерін тауып байланыс теңдеуіне қоямыз да, у-тің сәйкес мәндерін анықтаймыз. Нәтижесінде шартты нүктелерін алмасақ, онда Лагранж көбейткіштері әдісін қолданамыз.
Лагранж көбейткіштері әдісі.
z=f(x; y) функциясын
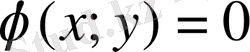 болғанда экстремумге зерттеу үшін:
болғанда экстремумге зерттеу үшін:
- Көмекші Лагранж функциясын құрастыру керек:
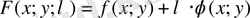 (1)
(1)
Мұндағы
 көмекші белгісіз;
көмекші белгісіз;
- дербес туындыларын тауып әрқайсысын нөлге теңестіріп шыққан үшбелгісі бар үш теңдеуден тұратын жүйені есептеу керек.
Жүйенің шешуінің нәтижесінде функцияның шартты экстремумы бар болуы мүмкін нүктелерін табамыз. Бірақ тапқан нүктелері шартты экстремум болмауы да мүмкін, себебі, жүйе шартты экстремумның тек қажетті шартын білдіреді.
1 Мысал:
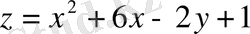 функциясын, х және у айнымалылары
функциясын, х және у айнымалылары
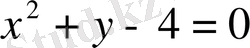 теңдеуімен байланысты болған жағдайда экстремумге зерттеу керек.
теңдеуімен байланысты болған жағдайда экстремумге зерттеу керек.
Δ байланыс, теңдеуді
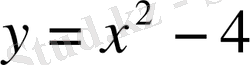 параболасы болады. Берілген z функциясында
параболасы болады. Берілген z функциясында
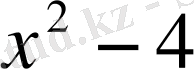 арқылы алмастырып
арқылы алмастырып
немесе
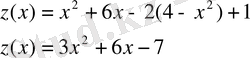
функциясына келеміз.
Шыққан z(x) функциясын экстремумге зерттейміз:
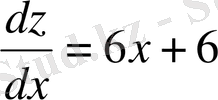
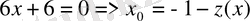 функциясының стационарлы нүктесі.
функциясының стационарлы нүктесі.
Екінші туындысын табамыз:
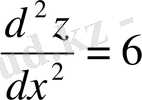
Екінші туындысы оң болғандықтан тапқан стационарлы нүктеде z(x) функциясының минимумы бар.
 мәнін байланыс теңдеуіне қоямыз:
мәнін байланыс теңдеуіне қоямыз:
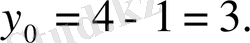 Сонымен,
Сонымен,
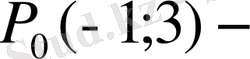 шартты экстремум нүктесі. Бұл нүктеде z=f(x; y) функциясының минимумы бар.
шартты экстремум нүктесі. Бұл нүктеде z=f(x; y) функциясының минимумы бар.
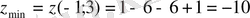 ▲
▲
Енді шартты экстремум нүктесін Лагранж көбейткіштері әдісін пайдаланып табайық.
- Көмекші Лагранж функциясын құрастырайық: Берілгені .
- дербес туындыларын табайық:
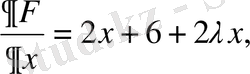
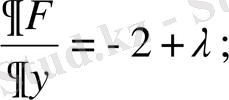
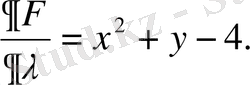
- Дербес туындылардың әрқайсысын нөлге теңестіріп жүйеге келеміз:
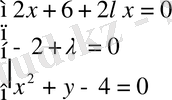
Екінші теңдеуден
 , онда бірінші теңдеуден x=-1, ал үшіншіден: у=3. Сонымен
, онда бірінші теңдеуден x=-1, ал үшіншіден: у=3. Сонымен
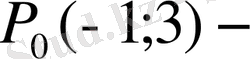 шартты экстремум нүктесі. Бұл жағдайда көмекші Лагранж функциясы келесі болады:
шартты экстремум нүктесі. Бұл жағдайда көмекші Лагранж функциясы келесі болады:
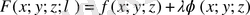 (2)
(2)
х, у және z айнымалылары екі
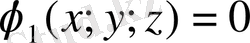 және
және
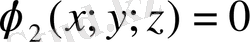 байланыс теңдеулері арқылы байланысты болуы мүмкін. Онда Лагранж функциясы келесі түрде жазылады:
байланыс теңдеулері арқылы байланысты болуы мүмкін. Онда Лагранж функциясы келесі түрде жазылады:
 (3)
(3)
2 Мысал: толық беті S-ке тең, көлемі ең үлкен болатын тікбұрышты параллепипедті табу керек.
Δ параллепипедтің қабырғаларын x; y; z айнымалылары
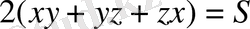 теңдігімен байланысты болатын ең үлкен мәнін табу керек.
теңдігімен байланысты болатын ең үлкен мәнін табу керек.
(2) формуланы қолданып, Лагранж функциясын құрастырамыз:
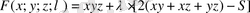
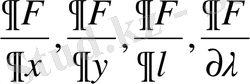 дербес туындыларын тауып, әр қайсысын нөлге теңестіріп, x; y; z,
дербес туындыларын тауып, әр қайсысын нөлге теңестіріп, x; y; z,
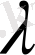 белгісіздері бар төрт теңдеулер жүйесін шығарамыз:
белгісіздері бар төрт теңдеулер жүйесін шығарамыз:
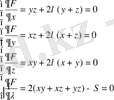
Бірінші үш теңдеуден x=y=z екені шығады. Онда төртінші теңдеуден
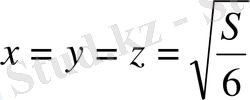
екені шығады.
Сонымен,
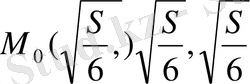 нүктесі - шартты экстремум нүктесі. Онда ізделген паралллепипед - қабырғалары куб
нүктесі - шартты экстремум нүктесі. Онда ізделген паралллепипед - қабырғалары куб
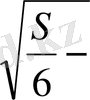 ға тең. ▲
ға тең. ▲
3
Мысал:
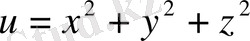 функциясын айнымалылары
функциясын айнымалылары
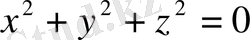 және
және
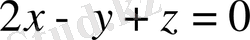 теңдеулерімен байланысты болғанда экстремумге зерттеу керек.
теңдеулерімен байланысты болғанда экстремумге зерттеу керек.
Δ айнымалылары екі байланыс теңдеуімен байланысты болғандықтан, Лагранж формуласының (3) формула бойынша құрастырамыз.

Мұндағы
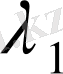 және
және
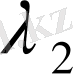 - белгісіз шамалар.
- белгісіз шамалар.
Дербес туындылары тауып, нөлге теңестіріп, шыққан теңдеулер жүйесін шығарамыз:
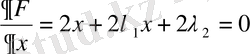 (1)
(1)
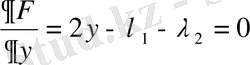 (2)
(2)
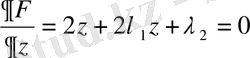 (3)
(3)
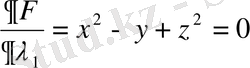 (4)
(4)
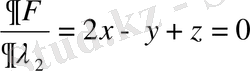 (5)
(5)
(1) теңдеуден
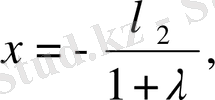 ал (3) теңдеуден
ал (3) теңдеуден
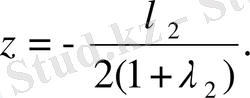 Осыдан x=2z екені шығады, онда (5) теңдеуден y=5z шығады. (4) теңдеуге x=2z және y=5z қоямыз:
Осыдан x=2z екені шығады, онда (5) теңдеуден y=5z шығады. (4) теңдеуге x=2z және y=5z қоямыз:
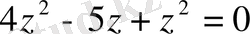 немесе
немесе
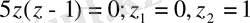 онда сәйкесінше
онда сәйкесінше
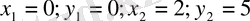
Сонымен, екі
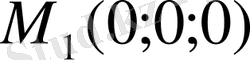 және
және
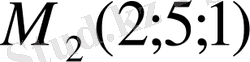 шартты экстремум нүктелерін табамыз. Бірінші нүктеде
шартты экстремум нүктелерін табамыз. Бірінші нүктеде
 функциясының минимумы, ал екіншісінде - максимумы бар.
функциясының минимумы, ал екіншісінде - максимумы бар.
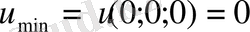
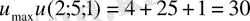 ▲
▲
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz