Экономикалық-математикалық модельдердің даму тарихы мен қолдану әдістері


Қазақстан Республикасының Білім және Ғылым министрлігі
Жоғарғы техникалық мектебі
Курстық жұмыс
Тақырыбы :
«Экономикалық математикалық модельдердің даму тарихы»
Орындаған:
Тексерген:
Орал 2012ж.
Мазмұны
Кіріспе . . . 3
І ТАРАУ. ЭКОНОМИКАЛЫҚ МАТЕМАТИКАЛЫҚ МОДЕЛЬДЕУ
1. 1 Математикалық модельдерінің ұғымы және даму тарихы . . . 5
1. 2 Сызықтық бағдарламалау есептерінің қойылымы . . . 9
1. 3. Экономикалық өсудің маңызды модельдерінің
бірі - салааралық баланс моделі . . . 11
IІ TAPAУ. СИМПЛЕКС ӘДІСІ ЖӘНЕ ОНЫҢ ҚОЛДАНЫЛУ АЛГОРИТМІ
2. 1. Симплекс әдістің теориясы . . . 16
2. 2. Симплекс әдісі туралы түсінік . . . 20
1. 3. Симплекс әдісі алгоритмі . . . 24
Қорытынды . . . 26
Пайдаланылған әдебиеттер тізімі . . . 28
Кіріспе
Математикалық модельдеу - кез келген құбылыстарды немесе күрделі физ. процестерді, аппараттарды олардың математикалық модельдерін құру арқылы зерттеу тәсілі; матем. модельді құру процесі. Математикалық модельдеу деп қажетті процесті немесе аппаратты сипаттайтын матем. теңдеулер жүйесін айтады. Математикалық модельдеу үшін кез келген матем. мүмкіндіктерді (дифференциалдық немесе интегралдық теңдеулерді, жиындар теориясын, абстрактылық алгебраны, матем. логиканы, ықтималдықтар теориясын, т. б. ) пайдаланады. Математикалық модельдеу. негізіне түпнұсқа мен модельдің айнымалы параметрлерінің біртектес немесе ұқсас теңдеулермен сипатталуы алынады. Математикалық модельдеу көбінесе, компьютерлер арқылы зерттеледі, сондықтан оны кейде компьютерлік модельдеу деп те атайды
Болашақ мамандар үшін қолданбалы математиканың ең маңызды салаларының бірі - математикалық модельдеу пәні: ол экстремалдық есептерді зерттеуге және олардың шешу әдістеріне арналған. Бұл пәнді оқу қарапайым есептердің математикалық модельдерін құрастыруда алғашқы қадам жасауға, олардың математикалық қойылуы мен шешу әдістерін үйренуге мүмкіншілік береді. Бұл пән бойынша белгілі білім қорын жеткізіп және оларды қолдануға үйретіп қана қоймай, ол сонымен қатар математиканы оқып-үйрену үшін қажетті студенттердің логикалық ойлауын және математикалық мәдениетін дамытады.
Математикалық модельдеу пәні жалпы ғылыми пән болып табылады.
Бұл пән жоғары математика курсынан кейін оқылуға тиіс: бұл жерде сызықтық алгебра мен шектелген өлшемдегі кеңістіктегі дөңес жиындар теориясының рөлі аса маңызды. табысты меңгеру үшін орта мектеп көлеміндегі элементарлық математиканы, сондай-ақ қатар оқылатын жоғарғы және сызықтық алгебраны, аналитикалық геометрияны, математикалық талдау элементтерін, сандық әдістерді білу қажет.
« Математикалық модельдеу» пәнін оқытудағы мақсат сызықтық және сызықтық емес бағдарлама есептерінің модельдерін құру, олардың максимум және минимум мәндерін табу, екіжақты, транспорттық, вариациалау және ойын теориясының есептерін шешіп, математикалық статистика элементтерімен танысып, көпшілікке қызмет ету жүйесінің модельдерін шешуге үйрену болып табылады.
Көптеген математикалық модельдер универсалды болып келеді, яғни әртүрлі жүйелерді зерттеуге қолданылады. Математикалық модельдер қарастырылатын құбылыстар мен үрдістердің сандық заңдылықтарын анықтауға, сипатталатын факторлардың тәуелділігі мен өзара байланысын табуға мүмкіндік береді. Математикалық модельдердің дамуына өте күрделі есептеулерді жүргізетін электронды-есептегіш машиналарының көбеюі зор ықпал етті.
І ТАРАУ. ЭКОНОМИКАЛЫҚ МАТЕМАТИКАЛЫҚ МОДЕЛЬДЕУ
1. 1 Математикалық модельдерінің ұғымы және даму тарихы
Көптеген математикалық модельдер параметрлер мен айнымалылардан тұратын теңдеулер мен теңсіздіктер жүйелерінен тұрады. Айнымалы шамалар, мысалы, өндірілген өнім көлемі, капитал жұмсау, тасымалдау т. с. с., ал параметрлер өнімді өндіруге жұмсалған материал, уақыт, шикізат шығынының мөлшерін көрсетеді. Әрбір модельде айнымалылардың екі тобын көрсетуге болады. 1) Сыртқы айнымалылар - олардың мәндері модельден тыс және берілген; 2) Ішкі айнымалылар, олардың мәндері берілген модельді зерттеу қорытындысында анықталады.
Модельдеу үрдісінің нақты алгоритмі жоқ, бірақ модельдеу тәжірибесінде басшылықққа алатын анықталған принциптер бар.
Математикалық модельдердің құрылымдық және функционалдық түрлері бар. Құрылымдық модельдер жүйелердің құрылымын және оның элементерінің өзара әсерін зерттейді. Функционалдық модельдер жүйенің ішкі құрылысына байланыссыз әртүрлі жағдайдағы тәртібін талдайды.
Құрылымдық модельді оқып үйрену үстінде объектінің мазмұнын туралы, оның сыртқы жағдайларға әсері туралы информацияларды алуға болады. Ал функционалдық модельді зерттегенде объектінің әртүрлі реакцияларының сыртқы ортаға әсері туралы деректер алуға болады. Сонымен қатар объектінің құрылымын талдауға және құрылымдық модельдерді құруға мүмкіндіктер туады.
Экономикалық-математикалық модельдер жүйе жағдайын болашақты жоспарлау мен болжауға пайдаланады. Мұндай жағдайда модель оның негізінде қойылған белгілі бір алғы шарттарға сәйкес экономикалық үрдістердің ағымын көрсетеді. Жоспарлау мен болжау модельдерінде алғышарттарды дұрыс таңдау ерекше маңызды роль атқарады. Модель есептің шарты дұрыс қойылған кезде ғана нақты жүйелердің құрылысы мен функциясын дұрыс сипатайды.
Экономикалық-математикалық модельдер сипаттаулы және оптималды болып бөлінеді.
Экономикалық жүйелердің сипаттаулы моделі есептерді математикалық формула түрінде көрсетеді және жүйе жағдайы мен оның элементтерінің байланысын тереңірек ұғып үйренуге қолданылады. Мұндай модельдерге халық шаруашылығы және экономикалық аудандардың салааралық байланысының матрицалық моделі жатады. Осындай типті есептің модельдері анықталған алғашқы мәліметтері бойынша бір ғана шешімі болады. Бұл модельдердің негізгі кемшілігі - ең тиімді (оптималды) шешімін іздейтін шарттың жоқтығы.
Оптималды модельдерде экономикалық есептің мағынасы математикалық формула түрінде жазылады және ең тиімді шешімі табылатын шарт функция түрінде көрсетіледі. Бұл модельдер белгілі бір алғашқы мәліметтер бойынша есеп шартын қанағыттандыратын көптеген шешімдер және оптималдықтың критерийіне сәйкес тиімді шешім алуға мүмкіндік береді. Мұндай модельдерге өндірістік программаны оптималдау, кесіп-пішуді оптималдау, қоспа компоненттерін оптималдау, кәсіпорынды орналастыруды оптималдау, көлік есептерінің модельдері жатады.
Оптималдық модельдердің көпшілігінде оптиалдықтың бір ғана критерийі қарастырылады. Математикалық модельдерде сызықтық және сызықтық емес тәуелділіктердің әртүрлі түрлері қолданылады. Математикалық модельдеу үрдісінің негізгі бөлігі аппроксимация (жуықтау) - математикалық амалдарды (функция, теңдеу т. с. с. ) басқа қарапайым шамалар арқылы жуықтап табу болып табылады. Аппроксимацияның көмегімен күрделі есептерді жай есептерге, сызықтық емес теңдеулерді сызықтық теңдеулерге келтіреді. Модельденетін обьектінің белгілі бір уақытқа немесе уақыт аралығына сәйкес қасиеттерін сипаттайтын математикалық модельдер статикалық деп аталады.
Үрдістердің белгілі бір уақыт аралығындағы өзгерістерін зерттейтін модельдер динамикалық деп аталады. Детерминистикалық (латынша determino - анықтау) модельдер дегеніміз барлық параметрлері және сыртқы айнымалылары бірге тең ықтималдықпен анықталатын модельдер. Ықтималдық модельдерінде параметрлер мен сыртқы айнымалылар немесе олардың белгілі бір бөлігі тиісті ықтималдықтың үлестіруімен сипатталады. Анықталмағандықты есепке алатын модельдерге ықтималдық теориясының заңдарын қолдануға болмайды.
Математикалық модель жасау процесі өзара байланысқан бірнеше кезеңнен тұрады.
Бірінші кезең - есептің қойылуы. Бұл кезең зерттеудің мақсатын анықтаудан басталады.
Мысалы, кәсіпорын үшін өнім өндіру немесе жүк тасымалдаудың оптималды жоспарын құру немесе берілген материалды кесіп-пішудің оптималды нұсқасын табу қажет т. с. с. Зерттеудің мақсатына сәйкес жүйелерді жан-жақты талдап, оның құрылымы мен қызметін, ерекшелктерін ескеру керек.
Жүйелерді модельдеген кезде модельге есептің шешіміне әсер ететін, яғни қойылған мақсатқа қол жеткізетін факторлардың енуі шарт.
Екінші кезең - таңдалып алынған жүйелерге математикалық модельдер құру. Бұл кезеңде есепті формула түріне келтіру - математикалық тәуелділіктерді теңдеулер, теңсіздіктер түрінде құру жүргізіледі.
Алдағы уақытта есептердің математикалық формула түрінде жазылған өрнектерін есептің моделі деп атаймыз.
Үшінші кезең - құрылған модельге сәйкес есептің шешімін алу. Бұл кезеңнің негізгі есептерін қарастырайық. Біріншіден, модельге қажетті алғашқы ақпараттарды жинау, параметрлер мен сыртқы айнымалылардың сандық мәндерін анықтау қажет. Екіншіден, есептің шешімін алатын әдісті таңдап алу керек. Сандық экономикалық-математикалық әдістердің арасында кеңінен тарағандары симплекс әдісі және потенциал әдісі. Олар көптеген экономикалық есептерді шығаруға қолданылады. Бұл әдістермен шығаруға келмейтін есептер де кездеседі. Мұндай жағдайларда жүйелерді зерттеудің эвристикалық және имитациялық әдістері қолданылады.
Эвристика (грек сөзінен - табамын, ойлап табамын, ашамын) - зерттеушінің интуициясы мен жүргізген тәжірибесіне сәйкес шешілетін әдістердің жиынтығы.
Имитация - модельдеудің мүмкіндігін кеңейтетін жаңа бағыт болып табылады. Имитациялық модельдеуді нақты жүйелердің модельдеріне жүргізілген эксперимент ретінде түсінуге болады, ал жеке алғанда математикалық модельдеудің көмегімен алғашқы шарттарын өзгерте отырып жүргізілетін есептеу эксперименті. Имитация (латынша - еліктеу) - жасанды құралдардың көмегімен бір нәрсені жаңадан ендіру немесе еске түсіру.
Төртінші кезең - модель бойынша алынған қорытындыны тәжірибеде қолдану. Математикалық әдістердің көмегімен алынған шешімдер талданып, белгілі бір аралықта алғашқы ақпараттарға тигізетін әсері тексеріледі.
Уақыттың өзгеруіне сәйкес алғашқы ақпараттар өзгереді, сол өзгерістердің алынатын шешімдерге тигізетін әсерін білу аса маңызды.
1. 2 Сызықтық бағдарламалау есептерінің қойылымы
Тиімді шешім табу (ең үлкен немесе ең кіші шешім) мәселесімен ерте заманнан бастап көптеген оқымысты ғалымдар айналысты, сонымен қатар олар табылған әдістерді әртүрлі ғылым салаларында, оның ішінде: математикада, механикада, физикада т. б. ілімдерде қолдана білді.
Қандай есепті құрастырмасақ та, тиімді шешім табу үшін алдымен алдымызға мақсат қою қажет, ал мақсатты функция берілген жағдайды немесе шарттарды қанағаттандыруы керек. Мақсатты функцияға және шарттарға енген белгісіздер өте көп және үлкен дәрежелі болуы мүмкін. Егер есепке енген белгісіздердің дәреже көрсеткіші бірден артпаса, онда мұндай есептерді сызықты алгебра есептеріне жатқызады. Мұндай жағдайда есептің берілген шарттары сызықты теңдеу немесе теңсіздіктер түрінде беріледі.
Сызықтық бағдарламалау есебі былай анықталады.
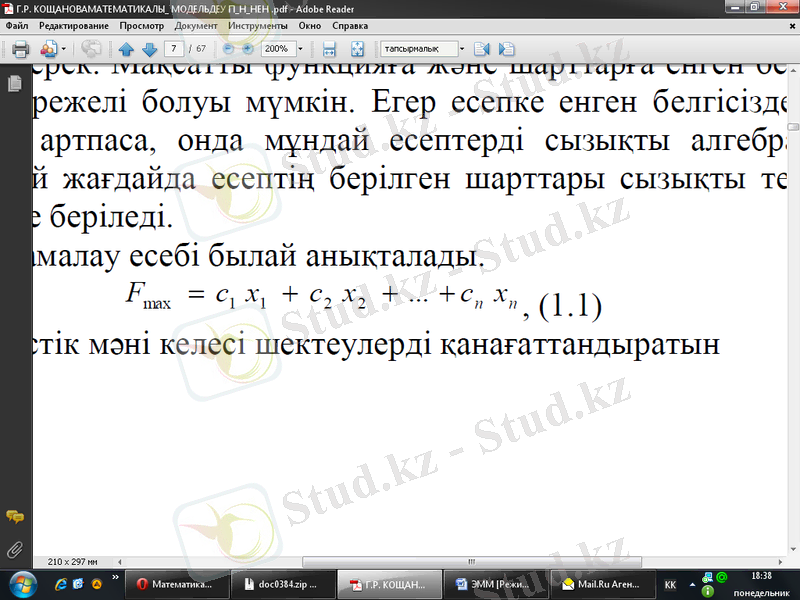
функцияның кризистік мәні келесі шектеулерді қанағаттандыратын
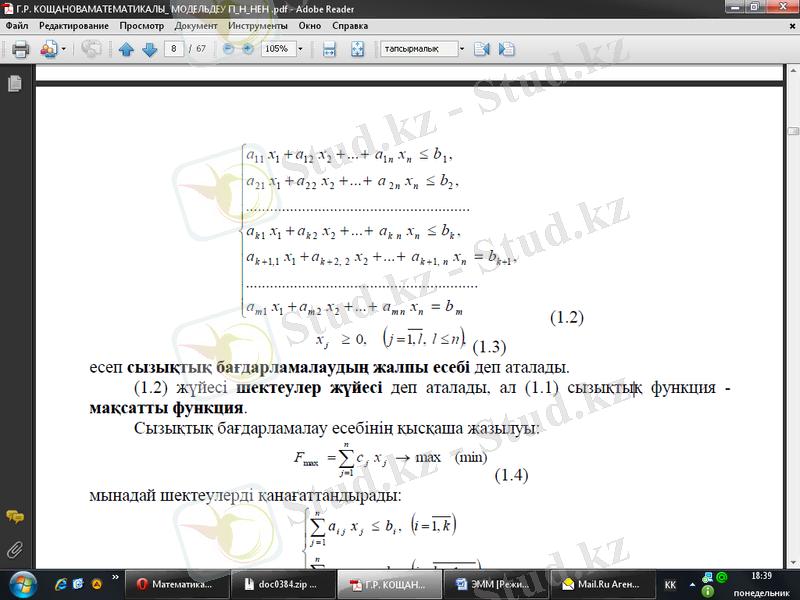
есеп сызықтық бағдарламалаудың жалпы есебі деп аталады.
(1. 2) жүйесі шектеулер жҥйесі деп аталады, ал (1. 1) сызықтық функция - мақсатты функция. Сызықтық бағдарламалау есебінің қысқаша жазылуы:
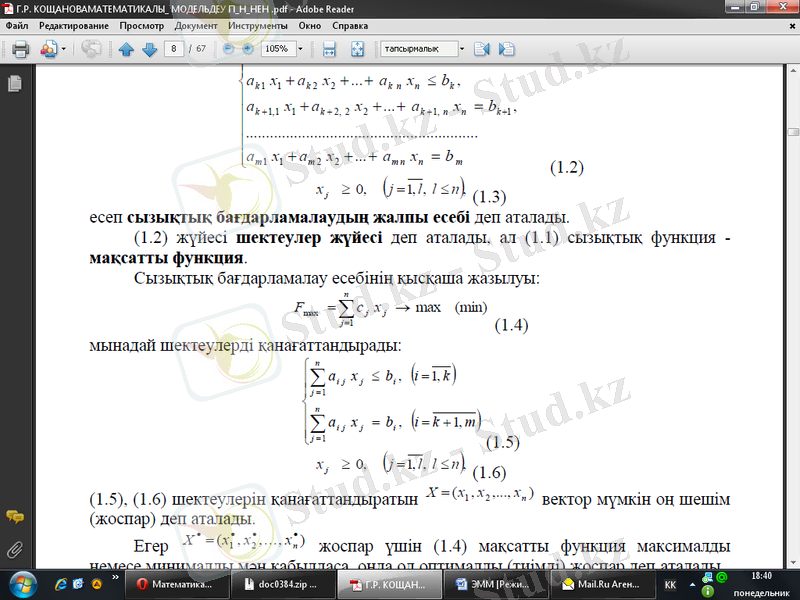
(1. 5), (1. 6) шектеулерін қанағаттандыратын X=(x 1 , x 2 …. . x n ) вектор мүмкін оң шешім (жоспар) деп аталады.
Егер
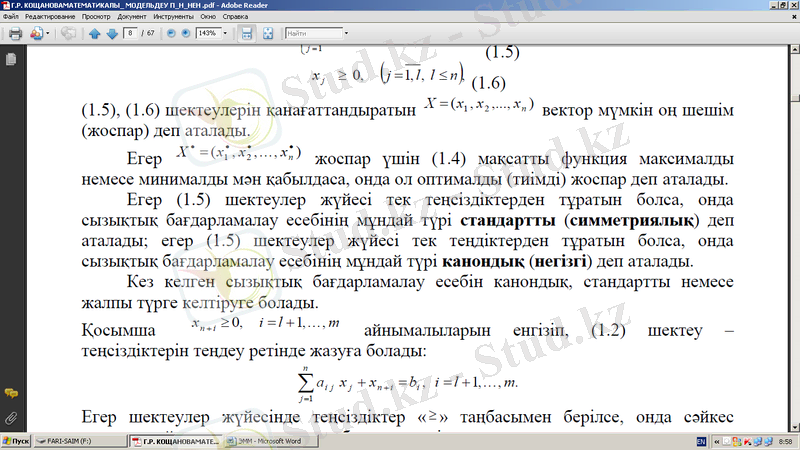 жоспар үшін (1. 4) мақсатты функция максималды немесе минималды мән қабылдаса, онда ол оптималды (тиімді) жоспар деп аталады.
жоспар үшін (1. 4) мақсатты функция максималды немесе минималды мән қабылдаса, онда ол оптималды (тиімді) жоспар деп аталады.
Егер (1. 5) шектеулер жүйесі тек теңсіздіктерден тұратын болса, онда сызықтық бағдарламалау есебінің мұндай түрі стандартты (симметриялық) деп аталады; егер (1. 5) шектеулер жүйесі тек теңдіктерден тұратын болса, онда сызықтық бағдарламалау есебінің мұндай түрі канондық (негізгі) деп аталады.
Кез келген сызықтық бағдарламалау есебін канондық, стандартты немесе жалпы түрге келтіруге болады.
1. 3. Экономикалық өсудің маңызды модельдерінің
бірі - салааралық баланс моделі
Салааралық баланс - келешектегі экономикалық салалық құрылымының негіздеме құрал ретінде аймақаралық байланыстарды ұтымды қамтамасыз етудің баланстық әдісі.
Экономикадағы баланс экономика арасында өзгермелі бай-ланыс орнатады. Олар екі немесе экономикалық (мемлекеттік бюджет, табыстар және тұрғындардың шығындары, сыртқы экономикалық баланс, төлем балансы және т. б. ) көбірек бөлігінің теңдігін көрсететін кесте немесе теңдеу түрінде көрсетілген.
1952 жылы Нидерландияда алғаш рет ҰЕЖ-ге салааралық баланс енгізілді. Бұл баланс өндіріс сферасының 26 саласы бойынша құрылды және 1938, 1946-1951 жж. қамтиды. Мұнан былай салааралық балансты құрған елдердің барлығы оны ұлттық есеп жүйесіне енгізді.
Халық шаруашылығы балансының ұлттық есеп жүйесінен елеулі өзгешеліктер бола тұра ҰЕЖ -нің дамуына өз әсерін тигізді. Өйткені Кеңестер Одағының статистикалық ұйымдары алғашқы халық шаруашылығы балансын 1925-1926 жылдары құрды, яғни ХШБ ҰЕЖ-нің алғашқы зерттеулерінен бұрын пайда болды.
ХШБ-ның алғашқы зерттеулері экономика салаларының байланысын көрсететін кестелерден құралды. Бұл кестелер салааралық баланстың болашақтағы үлгісі еді. Халық шаруашылығы балансының негізгі ережесі - материалдық өнідіріс сферасы мен өндірістік емес сфераны ажырату, материалдық өндірістің өзін өндіріс құрал жабдықтарының (І бөлігі) және тұтыну затарының өндірісі (ІІ бөлігі) деп екіге бөлу.
Осы теория ббойынша қоғамдық жиынтық өнім екі формада ұдайы өндіріледі:
а) натуралды затты
б) құнды. Натуралды-заттық формасы орын толтыру қорына(өндірістік тұтыну) және қорлану қорына бөлінеді. Ал құнды формасы бойынша қоғамдық жиынтық өнім екі бөліктен тұрады. Ол затқа айналған құн(С) және жаңа жасалған құн(V+м) .
Салааралық байланс («шығындар -өім шығару» кестесі) үйлесімді саларалық арақатынастарды, байланыстарды көрсетеді. Бұл кесте төрт квадранттан тұрады және халықаралық стандартты салаарлық классификаторда көрсетілген салалардың басым көпшілігі үшін құрылды. Кесте жеке кәсіпорындар мен экономикалық салалары арасындағы байланыстарды талдауға мүмкіндік берді. Өзінің мазмұны жағынан салааралық баланс өндіріс шотына ұқсас.
Салааралық баланстың теориялық негіздері бірінші бесжылдыққа әкелген жылдары СССР-да жасалған болатын. Бірақ рәсімделген түрінде алғашқы болып американдық экономист В. Леонтьев "шығын шығару" деген атпен шығарды. АҚШ-тағы салааралық байланыс шахматтық тип түріндегі кестелерді және сызықтық алгебра құралын қолдану арқылы 30-жылдары В. Леонтьевпен американдық экономиканы зерттеу үшін қолданылған болатын.
кәсіпорындар мен мекемелердің қаржы жағдайын, шаруашылықтың кірісі мен шығысын (актив, пассив), т. б. тепе-теңдіктерді сипаттайтын өзара байланысты көрсеткіштердің белгілі бір жүйесі;
ақша мен тауардың кірісі мен шығысын бейнелейтін, бір-бірімен тең екі жақтық сандық қатынас. Мысалы, тауарды шетке шығару мен сырттан алып келу көрсеткіштері тең болып, жеткілікті қоры жасалып отырса ғана оны өндіру мен тұтыну балансының теңдігі сақталады. Баланстар ел экономикасын (бюджеттік баланс, төлем балансы, салааралық баланс), өнеркәсіп пен фирмалардың қаржы жағдайларын (бухгалтерлік баланс, негізгі қорлардың балансы, қаржы балансы) халықтың кірісі мен шығысын (отбасының кірісі мен шығысы, тұтыну бюджеті) талдауға, есептеуге, жоспарлауға пайдаланылады.
Экономикада баланстың төмендегідей түрлері қоланылады:
1) айналмалы қаржы Балансы - белгілі бір уақыт аралығындағы фирманың, кәсіпорынның, бірлестіктің кірісі мен шығысының бір-біріне сәйкестігін бейнелейтін кесте, онда қаржы қозғалысының сипаты көрініс табады;
2) Бухгалтерлік балансбухгалтерлік Баланс - кәсіпорындардың, фирмалардың, мекемелердің, т. б-дың жалпы ақша қаражаттарының белгілі бір мерзім ішіндегі орналасу, пайдалану жағдайларын жинақтап көрсететін кесте. Құрылымы жағынан бухгалтерлік Баланс екі жақты. Кестенің активті жағы - кәсіпорын мен фирма қаржысының құрамы мен орналасуын, ал, пассивті жағы- бұл қаржылардың қайдан түсетінін көрсетеді. Актив пен пассивтің қорытындысы тепе-тең болады;
3) еңбек ресурстарының балансы - еңбек қорларын пайдаланудың түрлі жақтары, толықтыру мен азаюы ескеріле отырып жасалады;
4) есептеу балансы - ақша талабы мен мемлекеттің сыртқы балансы туралы белгілі күнге (әдетте жыл басына) немесе белгілі уақытқа (жылға) берген міндеттемесінің арақатынасы;
5) жинақталған қаржы балансы - халық шаруашылығының қаржы қорларын құрудың және пайдаланудың негізгі шамаларын (пропорция) бейнелейтін қаржылық көрсеткіштер жүйесі;
6) жұмыс уақытының балансы - өндіріс қызметкерлері жұмыс уақытының қорларын және оларды әрбір жұмыс түрлеріне қарай пайдалануын бейнелейтін баланс;
7) материалдық баланс - материалдық ресурстардың (заттық қорлардың) пайда болу көздері мен түсу көлемі мен олардың тұтыну көлемінің сәйкестігін бейнелейтін баланс;
8) капитал мен несие қозғалысының балансы - мемлекеттік және жеке капиталдың, сондай-ақ, берілген және алынған халықар. несиелердің арасалмағын көрсететін баланс;
9) негізгі қорлар балансы - өндіріс қуаттары мен құрал-жабдықтарының қозғалысын сипаттайтын көрсеткіштер жүйесі. Негізгі қорлар балансы ұдайы өндірістің негізгі қорларының көлемі, құрылымы, олардың қозғалысы, арақатынасы мен өсу қарқыны жайында мәліметтер алу мақсатымен жүргізіледі;
10) сауда балансы - белгілі бір уақытта шетке тауар шығарудан және сырттан тауар әкелуден түскен кіріс пен төлемнің арақатынасы;
11) сыртқы сауда балансы - белгілі уақыт аралығындағы (ай, тоқсан, жыл) шетке шығарған және сырттан әкелінген тауар құнының арақатынасы;
12) табыс пен шығыс балансы - белгілі бір мерзім ішіндегі кіріс пен шығыстың көздері, мөлшері көрсетілген және олардың тепе-теңдігі не болмаса бір жағының екінші жағынан артықтығы бейнеленген қаржы есебі;
13) тарату балансы - фирманың, кәсіпорынның, бірлестіктің заңды тұлға ретінде жұмысын тоқтатқан күнгі мүліктік жағдайын бейнелейтін бухгалтерлік есеп;
14) төлем балансы - белгілі уақыт ішіндегі валюта түсімі мен төлем қабілетінің арақатынасы. Мемлекеттің жан-жақты сыртқы экономика байланысын айқындайды. Төлем балансы күнделікті қарапайым операциялардан, капиталдар мен несиелердің қозғалыс Баланстарынан тұрады. Ағымдағы күнделікті төлем балансына: сауда балансы, шетке шығарылған тауар мен әкелінген тауар құнының арақатынасы, көрсетілген қызметке төленген және одан түскен қаржылар, шет ел туризмі есептері, саудадан тыс төлемдер мен түсімдер (жеке акция аудару, зейнетақы, сыйлықтар, шет елде елшілік ұстау қаражаты, шет елге орналасқан қарулы күш қаражаты, т. б. ), шетелдік акция қаражатын жұмсауға байланысты кіріс пен төлемдер жатады;
15) халықаралық борыш балансы - бір елдің екінші елге уақтылы өтеу мезгіліне байланыссыз, белгілі бір мерзімде жиналған барлық ақшалай және мүліктей талаптары мен міндеттері;
16) халықаралық есептесу балансы - бір елдің екінші елге қоятын қаржылай талабы мен міндеттерінің, түсімі мен төлемінің арақатынасы.
17) халық шаруашылығы балансы - ұлғаймалы ұдайы өндірістің қарқыны мен көлемін бейнелейтін экономика кестелер мен негізгі көрсеткіштер жүйесі. Халық шаруашылығының дамуындағы қарым-қатынастар мен пропорцияларға және жоспарлаудағы әдістер мен әдістемелерге тығыз байланысты болады. Баланстың бұл түрі өндіріс пен қоғамдық бөліністің өзара сәйкесу деңгейін көрсетеді.
Баланс (фр. balance, сөзбе-сөз-таразы, лат. bilanx-қос табақты таразы) . Нендей бір өзгермелі құбылыстың ара салмаған немесе тепе-теңдігін сипаттайтын көрсеткіштер.
IІ TAPAУ. СИМПЛЕКС ӘДІСІ ЖӘНЕ ОНЫҢ ҚОЛДАНЫЛУ АЛГОРИТМІ
2. 1. Симплекс әдістің теориясы
АҚШ- та сызықты программалау 1947 жылдан бастап, Дж Данциг -- еңбектерінде қалыптаса бастады. Ол, кейін симплекс әдіс деген атақ алған сызықты программалау есептерін шығарудың қолдануға жеңіл, сандық әдісін ойлап тапты.
Қойылған кедергілерге қарамастан Л. В. Канторович та экономикалық идеяларға құрылған математикалық жұмыстарына қайта оралып, Д. Ж. Данцигтен тәуелсіз симплекс әдістің идеясына келді. Оның бұл еңбектерін жоғары бағалаған Д. Ж. Данциг «Канторович өндіріске қатысты есептердің үлкен, маңызды класын математикалық тұрғыдан сипаттауға көз жеткізген бірінші адам болды. Оның ойынша бұлай сипаттау есепке сандық тұрғыдан қарауға және оны сандық әдістермен шығаруға мүмкіндік береді . . . Канторович алғашқы табылған мүмкін шешімді пайдалануға негізделген әдісті сипаттады . . . » -деп, өзінің сызықты программалаудың тарихына арналған еңбегінде атап өтті.
Симплекс - әдістің алгоритмі қадамдарын тізбекпен реттеп жазайық та, оның есептелу жолын мысалмен көрсетейік. Бұл тура симплекс - әдіс деп аталады. Сонымен, алгоритм мынадай қадамдардан тұрады:
Қадам 0. Бастапқы базисті шешімді таңдау және алғашқы симплекс-кестені толтыру (бір рет орындалады) .
Қадам 1. Ағымдағы шешімді тиімділікке тексеру. Егер шешім тиімді болса, онда есептеуді аяқтаймыз, әйтпесе келесі қадамға көшеміз:
Қадам 2. Шешімді жетілдіру бағытын таңдау және параметрлерін анықтау.
Қадам 3. Жаңа «жетілген»(лучшему) шешімге көшу. Қадам 1-ге қайта оралу.
Өнім шығаруды жоспарлау есебін симплекс-әдіспен шығару жолын, келтірілген алгоритмдерді пайдаланып шығарайық.
Теңдеу- шектеулермен берілген СПЕ қойылсын.
Қадам 0. Бастапқы базисті шешімді таңдау.
Базисті айнымалылар үшін қосымша
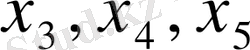 - айнымалыларын таңдаймыз. Сонда
- айнымалыларын таңдаймыз. Сонда
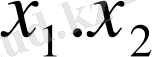 - еркін айнымалылар болады да базисті шешім
- еркін айнымалылар болады да базисті шешім
Х 0 = (0, 0, 24, 12, 8) - түрінде болады.
Қосымша айнымалылардың экономикалық мағыналарына тоқталайық:
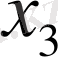 - 1-ші түрлі шикізаттың қалдығы,
- 1-ші түрлі шикізаттың қалдығы,
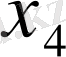 - 2-ші, ал -
- 2-ші, ал -
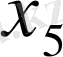 3-ші түрлі шикізаттар қалдығы. О. б., бастапқы шешімді былай түсіндіруге болады: егер ешқандай өнім шығармасақ
3-ші түрлі шикізаттар қалдығы. О. б., бастапқы шешімді былай түсіндіруге болады: егер ешқандай өнім шығармасақ
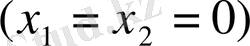 , онда шикізат қалдықтарының бәрі де қалдыққа көшеді
, онда шикізат қалдықтарының бәрі де қалдыққа көшеді
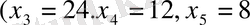 . Бұл жағдайда табыс түспейді, яғни
. Бұл жағдайда табыс түспейді, яғни
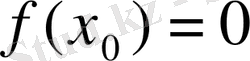
СПЕ-нің бастапқы мәліметтерін және бастапқы шешім туралы ақпараттарды симплекс-кестеге енгіземіз (n-айнымалылар саны, m-шектеулер саны) .
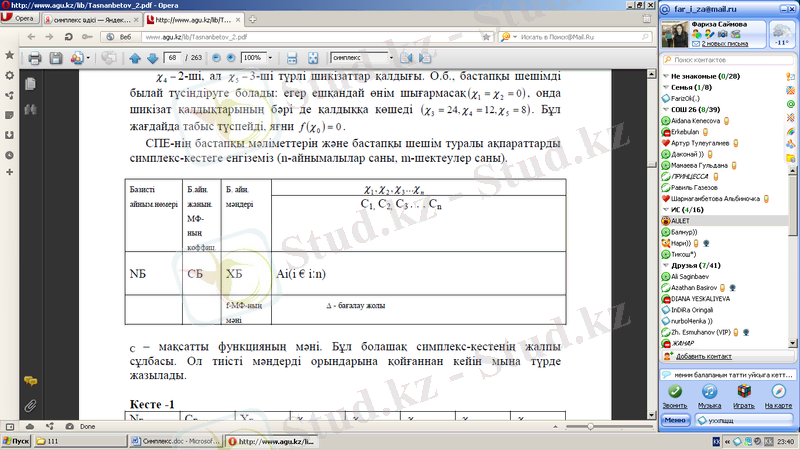
С - мақсатты функцияның мәні. Бұл болашақ симплекс-кестенің жалпы сұлбасы. Ол тиісті мәндерді орындарына қойғаннан кейін мына түрде жазылады.

Бастапқы базисті шешімге сәйкес алынған кестенің ең төменгі жолын толтыруға түсініктеме берейік.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz