Кодтауды негізгі анықтамалары

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 27 бет
Таңдаулыға:

Экономикалық технологиялар колледжі

КУРСТЫҚ ЖҰМЫС
Тақырыбы:
Кодтау

Орындаған: 9-522 топ студенті Тлешова Асем
Тексерген: арнайы пәндер оқытушысы Құдайбергенов М.Ф.

Орал, 2014ж.

Жоспары
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .3

Негізгі бөлім
1. Кодтауды негізгі анықтамалары ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..5
2. Кері кодтау ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 9
3. Ақпарат көздерінің сандық стационарлық кодтаушылары ... ... ... ... ... ... ... 11

Екінші бөлім
1. РИД-СОЛОМОН КОДТАРЫНЫҢ ЕРЕКШЕЛІКТЕРІ ... ... ... ... ... ... ... ... 13
2 РИД-СОЛОМОН КОДТАРЫНЫҢ ИМПУЛСЬТІ КЕДЕРГІЛЕР
КЕЗІНДЕ ТИІМДІЛІГІ ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..17
3 РИД-СОЛОМОНННЫҢ КОДТАЛУЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..2 1
4 СИСТЕМАТИКАЛЫҚ ФОРМАДА КОДТАУ ... ... ... ... ... ... ... . ... ...22
5 РИД - СОЛОМОН ДЕКОДТАЛУЫ ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... 23

Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 31
Пайдаланылған әдебиеттер тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... 33

Кіріспе
Қазіргі ақпараттық ғасырда деректерді жіберу, сақтау және іздеу үшін тек қана оның жылдамдығы маңызды емес, сонымен қатар оның қатесіздігі маңызды. Ақпаратты өңдеу және сақтау, жіберу құрал-жабдықтарының қазіргі даму сатысында барлық үлкен өзектілік жоғарғы қорғаушылықты қамтамасыз ету мәселесінде жатыр, оның бәрi өсетiн сапаға қойылатын талаптарымен және нақты жүйелердiң сенiмдiлiгiне шартталған. Кодтау және декодтау тәсілдерін таңдау, және олардың жүзеге асыру әдістерін. Сонымен бірге тезәрекеттілігі (кодтау және декодтау жылдамдығы), жүзеге асырылу қиындығы (бағдарламаның көлемі немесе құрылғылардың шағыны), әмбебаптылығы сияқты көрсеткіштер де ескеріледі. Барлық параметрлерді ең жақсы жағдайда қамтамасыз ету мүмкін еместігі анық, және әрбір нақты жағдайда шешімді жеке-жеке жағдайларда қабылдау керек.
Кодтау (кодирование; coding; кодировать; encode) -- мәліметтерді олардың алдын ала тағайындадған кодтық комбинацияларымен бейнелеу немесе мәліметтер элементін (символдар жиынын) олардың кодтық комбинацияларымен сәйкес келтіру; программалау процесі.
Ақпараттың 8 биттік (байттық) кодтауын 7 биттік кодтауға түрлендіру. Мұндай түрлендірудің қажеттілігі кейбір желілік программалардың мәліметтерді тек 7 биттік кодтауда жеткізе алатындығынан туындайды. Байттық мәліметгерді осындай арналармен тікелей жеткізу ақпараттың бұрмалануына жол береді. Белгілі бір ереже бойынша дискреттік хабарды дискреттік сигнал түріне түрлендіру (аудармалау), яғни шарттаңбаларды қолдану.
Кодтау бланкі (программаны жазуға арналған бланк, стандартты бланк) (бланк кодирования (бланк для записи программы, стандартный бланк); doding (program) sheet) -- алғашқы мәліметтер мен алғашқы программаның операторларын (командаларын) компьютерге енгізу мақсатымен оларды тізбектік жазуға арналған бланк. Бланкіге ақпарат жазу берілген тілде қарастырылған ереже бойынша орындалады.
Кодтау жүйесі (система кодирования; system of coding) -- объектілерді кодтармен бейнелеу ережелерінің жиыны, кодтау ережесі мен символдар жиынтығы; код. Цифрлі деректерді аналогтік және цифрлі кодирлеу.
ТКЖ - нің бір түйінінен деректерді басқаға жіберу байланыстың барлық битінен жүйелі беріліспен жүзеге асады.
Аппараттық сигналдар деп - шектеулі диапазон шегінде кейбір шамалар мәндерінің сансыз мөлшерін көрсете алады.
Цифрлі (дискретті) сигналдар мәндердің біреуіне немесе түпкілікті наборға ие бола алады. Аналогтік сигналмен жұмыс жасағанда кодирленген деректерді беру үшін синусоидальді формадағы аналогты негізгі сигнал пайдаланылады, ол цифрлі сигналдар жұмысында - екідеңгейлі дискретті сигнал. Аналогты сигналдар бұрмалануға сезгіш, есесіне деректерді кодирлеу мен декодирлеу цифрлі сигналдар үшін қарапайым жүзеге асады.
Аналогты кодирлеу телефонды байланыс бойынша цифрлі деректерді беру кезінде қолданылады. Әдетте ЭЕМ келіп түсетін цифрлі деректер модулятор - демодулятор көмегімен аналогты формаға түрленеді.

Негізгі бөлім
1. Кодтауды негізгі анықтамалары
Кодтау теориясы -- компьютингтің дамуына өз үлесін қосқан математиканың бір облысы болып табылады. Оның таралу облысы мәліметтерді нақты каналдар бойынша беру, ал оның пәні берілген ақпараттың нақтылығын қамтамасыз ету болып табылады. Кейбірде кодтау теориясын шифрлеумен шатастырады, бірақ ол дұрыс емес: криптография кері есепті шешеді, оның мақсаты - мәліметтерден ақпаратты алуды қиындату.
Кодтау теориясы мәліметтерді жоғалтпай алуды қамтамасыз етеді.
Мәліметтерді кодтаудың қажеттілігімен алғашқы рет жүз елу жыл бұрын тап болды. Каналдар өте қымбат және сенімсіз болғандықтан телеграммаларды жіберудің өте тиімді жолдары қарастырылды.1845 жылы пайдалануға арнайы кодтау кітаптары шықты; олардың көмегімен телеграфистер қолмен мәліметтердегі ұзақ сөйлемдерді қысқа кодтармен алмастырды. Сол кездері мәліметтердің жіберілуінің дұрыстығын тексеру үшін жұптық бақылау әдісі қолданылды, бұл әдісті перфокарталардың дұрыстығын тексеру үшін компьютердің бірінші және екінші буындарында да қолданылды. Ол үшін ең соңғы мәліметтер колодасына арнайы дайындалған бақылау сомасы бар картаны салған. Егер енгізу құрылғысы сенімсіз болса (немесе колода тым ұзын болған жағдайда), онда қате тууы мүмкін. Оны жөндеу үшін картадағы сомамен сәйкес келмегенше процедураны қайталай беретін. Бұл сұлбаның ыңғайсыз болғанымен қатар, ол екі есе қателер жіберетін. Байланыс каналдарының дамуымен қатар бақылаудың өте тиімді механизмі керек болды.
Бұл мәселенің теориялық шешімін алғашқы болып ақпараттың статистикалық теориясынының негізін қалаушы Клод Шеннон ұсынды. Шеннон өз заманының жұлдызы болды,ол АҚШ-тың академиялық элитасынынң мүшесі болған. Ванневар Буштың аспиранты болып, ол 1940 жылы жасы 30 жетпеген оқымыстыларға берілетін Нобель атындағы сыйлыққа ие болды (Нобель премиясымен шатастырмаңыздар). Bell Labs жұмыс істеп жүріп Шеннон Мәліметтерді жіберудің математикалық теориясы (1948) атты жұмыс жазды, ол жұмыста Шеннон каналдың жіберу мүмкіндігі мәліметтердің энтропия бастауынан жоғары болса, онда мәліметтерді ешқандай ақаусыз жіберілетіндей етіп кодтап қоюға болатынын дәлелдеді.Бұл түйіндеме Шеннонның көптеген дәлелдеген теоремалардың біреуінде бар. Сонымен қатар, ол каналда шудың бар болуына қарамастан мәліметтің жіберілу мүмкіндігінің теориялы түрде дәлелдеп берді.Шеннонның Мичиган штатында өзінің туып өскен қаласында орнатылған ескерткішінде ойып жазылған формуланы C = W log ((P+N)N) Альберт Эйнштейннің E = mc2 формуласының мәнімен салыстырады.
Шеннонның еңбектері ақпараттар теория облысындағы ары қарай зерттеулерінде өз ықпалын тигізді, бірақта оларда инженерлік практикалық қосымшасы бар болмады. Теориядан практикаға алмасу Ричарда Хэммингтің жұмысынан байланысты болды. Ол Шеннонның Bell Labs бойынша әріптесі болды және кодтар класын ашқандығы үшін әйгілі болды, оларды Хэмминг коды деп атады. Өзінің жаңалығын Хемминг 40 жылдардың ортасында Bell Model V есептеуіш машинасының перфокарталармен жұмыс жасау қолайсыздығынан ашты деген аңыз бар. Оған операторлар жоқ болғанда, яғни демалыс күндерде машинамен жұмыс жасауға мүмкіндік берді және ол өзі енгізулермен жұмыс жасады. Хемминг байланыс каналдарындағы, сонымен қатар компьютерлердегі ақпараттарды беру магистральдарында, ең бастысы жад пен процессор арасындағы қателерді түзете алатын кодты ұсынды. Хемминг коды Шеннон теоремасында көрсетілген мүмкіндіктерді практикалық түрде қалай іске асыруға болатындығын көрсетеді.
Хемминг өзінің мақаласын 1950 жылы жарыққа шығарды, бірақта ішкі жазбаларда кодтау теориясы 1947 жылмен белгіленген. Сондықтанда кейбіреулер кодтау теориясының атасы ретінде Шеннонды емес, Хеммингті атау керек деп ойлайды. Бірақта, техника тарихында алғашқыны іздеу пайдасыз нәрсе.
Хемминг бірінші болып қателерді түзейтін кодтарды (Error-Correcting Code, ECC) ұсынғандығы анық екенін білеміз. Бұл кодтардың қазіргі заманғы модификациялары барлық ақпараттарды сақтау жүйелерінде және жад пен процессор арасындағы алмасулар үшін қолданатыны белгілі. Олардың бір нұсқасы Рид-Соломонның коды компакт-дискілерде қолдланылады. Хэмминг тәсілі бойынша жасалынған көптеген кодтар нұсқалары бар, олар кодтау алгоритмдері бойынша және тексеретін биттер саны бойынша айырмашылықтары бар. Мұндай кодтарға планетааралық станциялармен космостық байланыс жасау үшін ерекше көңіл беріле бастады, мысалы, Рид-Мюллердің кодтарын 7 ақпараттық битке 32 тексеруші бит немесе 6 ақпараттық битқа - 26 тексеруші биттар келетін болды.
ECC жаңа кодтардың бірі ретінде LDPC (Low-Density Parity-check Code) кодын айтуымызға болады. Негізінде олар отыз жыл бұрын танымал блған, бірақта қазіргі уақытта оларға ерекше көңіл бөлінуде. LDPC коды 100-пайыздық анықтылығы бомағанмен, ол қатенің мүмкіндігін керекті нәтижеге дейін жеткізуімізге мүмкіндік береді және сонымен қатар каналдың жіберу мүмкіндігі максимальді толық түрде қолданылады. Оларға турбокодтар (Turbo Code) өте жақын келеді, олар алыс космостағы объектілермен жұмыс жасағанда өте қолайлы.
Кодтау теориясының тарихына Владимир Александрович Котельниковтың аты нық жазылған. 1933 году Материалах по радиосвязи к I Всесоюзному съезду по вопросам технической реконструкции связи-да ол өзінің О пропускной способности `эфира' и `проволоки' атты жұмысын жариялады. Бұл теоремада жіберілген сигнал ақпараттың жоғалтуынсыз қайтадан қалпына келетін шарттарды анықтайды.
Бұл теореманы әркім әрқалай атайды, соның ішінде WKS теоремасы (аббревиатура WKS взята от Whittaker, Kotelnikov, Shannon). Кейбір бастауларда Nyquist-Shannon sampling theorem және Whittaker-Shannon sampling theorem деп те аталады, ал өзіміздің жоғарғы оқу орындарының оқулықтарында жай ғана Котельников теоремасы деп кездестіреміз.
Кодтау теориясының тарихына Владимир Александрович Котельниковтың аты нық жазылған. Сандық байланыс каналы кодтаушысы мен хабарлама көзі арасында хабарламаны кодтаушы көздері қосылған. Хабарлама көздері сандық (компьютер, магнитті немесе оптикалық диск) немесе аналогты (телефонды, телевизиялық, телеметрикалық) сигналдар болып бөлінеді. Хабарламаны кодтау көздерінің міндеті болып, экономды түрде байланыс каналына хабарламаны сандық түрде көрсетуді жеткізу болып табылады. Хабарламаны кодтау көздерін тағы да хабарламаларды сығу құрылғысы деп те атайды. Егер сандық хабарлама көзі Rи жылдамдықпен екілік символдардың ағынын құрса, онда хабарлама кодтаушысының шығысында RRи жылдамдықты ақпараттық бит ағыны пайда болады. Бұл жылдамдықтардың қатынасы сығу коэффициенті болып табылады:
Ксғ= RиR,
мысалы, V.34 модемі үшін мәтіндік ақпараты бар сығу құрылғысы Ксғ=4 сығу коэффициентімен жасалған. Өйткені V.34 модемінің шығысында Rи=128кбитс болған кезде R= 32 кбитс мәніне ие.
Телефондық сигналдарды берген кезде Rи=64кбитс жылдамдықты да қоюға болады. Бұл беру жылдамдығы кезінде аналогты телефонды сигналдың телефон сигналының сапасын жоғалтпай сандық түрге айналуы жүреді. Бригадалық эксперттің тыңдауы көрсеткендей, жеткен сигналдың қайтадан аналогтыға ауысуы, яғни оны қайтадан кері аударып тыңдау кезінде ол сигналдың бастапқы кезінде шыққан сигналдан еш айырмасы жоқ екендігі анықталған.
Қазіргі кездегі түрлі-түсті телевизиялық сигналдар үшін оның сапасы жоғалмастан Rи= 256кбитс жылдамдыққа дейін жетеді. Бұл кезде телевизиялық сигналдың коммерциялық сапасында сығу коэффициенті Ксғ=50-100 мәніне жетеді.

2. Кері кодтау
Ақпаратты жеткізу үшін оның түрін өзгерту процесін кодтау деп атайды.. Бір белгі тобынан екінші белгі тобына көшіру ережесін код деп атайды. Ақпаратты кері кодтау декодтау (декодирование) процесімен тікелей байланысты. Ақпаратты сақтау, қабылдау, ұсыну, және өңдеу әдістері іс жүзінде ақпараттың ұсынылу түріне байланысты болады. Ақпараттың кодталуы кейде шифрау депте айтылады. Екілік алфабиты 0 және 1 таңбаларымен ұсынылады. Ақпаратты екілік код пен көрсету үшін, құрылғы екі күйді айыра білуі керек, мысалы; 1-құрылғыда тоқ бар, ал 0 жоғын , немесе 1-жоғары кернеу ,0 төмен кернеу. Тек екі түрлі мәні немесе немесе оған сәйкес код разряды бар , 0 немесе 1 мәндерін ғана қабылдай алатын сигналды бит деп атайды . Символдарды кодтау үшін 8 биттен тұратын котты байт деп атайды. 8 нөл мен бірлердің көмегімен яғни бір байттың көмегімен 256 символ кодталады. Символдарды кодттау кобинациаларының жиынтығын кодтау кестесі деп аталады.
ASCІІ коды. Есептеуіш техникасында ең көп пайдаланатын код-ASCLL коды - американдық апарат алмасудың стандарттық коды. Кодтау кестенің 16 жолы 16 бағаны бар . Кесте екі бөліктен тұрады ; стандарты, баламалы . Стандартты бөліктегі - бірінші 128 символдар , 0- ден 127-ге дейінгі коттар; Цифрлар, латын алфавитінің әріптерімен компьютер жұмысын басқаратын арнайы символдар. Баламалы бөліктегі-128-ден 255-ке дейінгі кодтар алфавиттер (орыс, қазақ) Ондық, екілік, оналтылық санау жүйелерінің сәйкестендіру кестесі бойынша кодтауға болады.
Ақпарат оны тіркейтін құрылғыға дыбыс, электромагнитті сәуле, физикалық әреект түрінде келіп түседі. Бұл әрекеттер сигнал деп аталады.
Сигнал дегеніміз- оның көмегімен адам немесе, құрылғы ақпарат қабылдайтын процесс. Сигнал ақпарат тасуыш. Ақпарат жіберу дегеніміз- сигналадар жіберу.
Ақпарат адам үшін жаңа, белгісіз болу керек. Хабар бізге ақпарат алу деген бізге жаңа түсінікті болуы керек. Сол салада біліміміз жеткілікті болуы керек. Егер ақпарат біз үшін толық, объективті,жаңа,пайдалы, әрі нақты болса ол біз үшін бағалы болады. Хабардың ақпараттың көлемі деп- хабардың ұзындығын, яғни символдар санын білдіреді.Ендеше техникада кез-келген сақталатын берілетін ақпарат көлемі ондағы берілетін ақпарат көлемі ондағы ең кіші өлшем бір екілік разрядқа немесе 1 битке тең болады. Бит (ағылшынша: binary digit; сонымен қатар сөздер ойыны: ағылшынша: bit -- аздап) - деректер сақталатын орын сыйымдылығының ең кіші өлшем бірлігі. Бүгінгі күні бит -- есептеу техникада ақпаратты өлшейтін ең кіші өлшем бірлік. Биттің кванттық компьютерлердегі баламасы q-бит болып табылады. Трит - есептеу техникасындағы ақпарат одан да бетер тығыз өлшем бірлігі. Трит өзі биттен үлкен, бірақ бір үштік разрядтың біреуі екілік разрядтың біреуінен кіші. Ақпаратты өлшеу бірлігі бір битке тең. Одан кейін 1 байт. Хабардың ақпараттың көлемі-бит немесе байтта өлшенетін оның ұзындығы.

3. Ақпарат көздерінің сандық стационарлық кодтаушылары

Ақпарат көздерін х1, х2,х3болсын, априорлық ықтималдық бойынша Р (хі)-тең болатын хіәріпін алайық. СондағыР (хі)априорлық ықтималдықта ақпараттар саны:

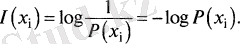
Сандық хабарламалардың орта ақпарат көздері энтропия көзі деп аталады:

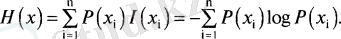
Егер екілік ақпарат көзі ықтималдығы q0тәуелсіз символын және ықтималдығы 1-q1 тәуелсіз символынкезектесіп береді.
Бол көздің энтропиясы былай болады:

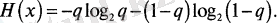
Хаффмен алгоритмі кодтай айнымалы ұзындықтағы кодтық қабаттардың көмегімен болатын кодтау жүйесі. Онда анықталған әріптер мүмкіндігінше қысқа кодтық сөздермен көрсетіледі. Бұл кезде кодтық сөздер қабылдау кезінде декодирленеді.
Хаффмен әдісі бойынша әріптер баған бойына жоғарыдан төмен қарай жазылады. Ол Р (хі) ықтималдығы бойынша кему ретімен орналасып, кодтық ағаш сұлбасын түзеді (1-сурет).
Кодтық ағаш құруды ықтималдырақх8 және х7символдарынан бастаймыз. Бұл екеуін жоғарғы бұтаққа біріктіріп, жоғарғысына 0, ал төменгісіне 1 саламыз. Бұл екі бұтақтың ықтималдығы бірігіп ортақ суммалық ықтималдық құрайды. Ары қарай келесі ықтималдықты бұтақтарды біріктіреміз және солай жалғаса береді. Кодтық сөздер қозғалыс кезінде оң жақ шетінен бастап шеткі сол жаққа дейінге жерден алынады. Ағаш бойымен жоғары қозғалғанда 0 символы, төмен қозғалғанда 1 сиволы 1-суретте көрсетілгендей алынады.

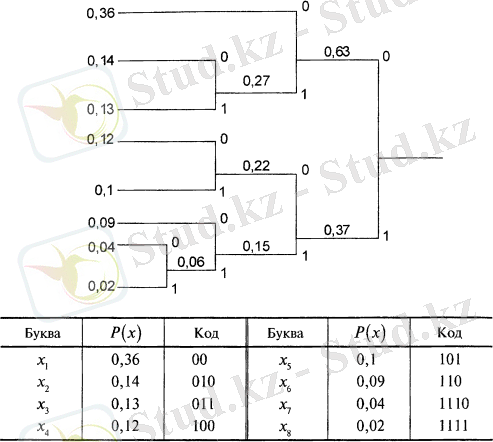
1-сурет. Айнымалы ұзындықтағы сөздерді кодтау

Екінші бөлім
1. Рид-Соломон кодтарының ерекшеліктері

Рид-Соломон кодтары (Reed-Solomon code, R-S code) - бұл екілік емес циклдық кодтар, оның символдары т - биттік тізбекті құрайды, мұндағы т - 2 санынан үлкен оң бүтін сан. (n, K) коды барлық п және k да т - биттік символдарда анықталған
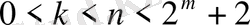(1.1.1)

мұндағы k - кодталуға жататын ақпараттық биттер саны, ал n - кодталатын блоктағы кодтық символдар саны. Рид - Соломонның өте нақты көптеген кодтары үшін (n,k)
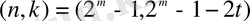(1.1.2)

мұндағы t - кодты түзей алатын символдағы қателік биттерінің саны, ал және 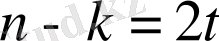- бақылау символдарының саны. Рид-Соломонның кеңейтілген кодын немесе 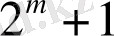арқылы алуға болады, бірақ одан артық емес.
Рид-Соломон коды ең үлкен минимальді арақашықтыққа ие, ол кодердің бірдей ұзындықтағы кіріс және шығыс блоктары бар сызықтық код үшін мүмкін болады. Екілік емес кодтар үшін өзара екі кодтық сөздердің арақашықтығы тізбектілігімен ерекшеленетін символдар саны сияқты анықталады. Рид-Соломон кодтары үшін минимальді арақашықтық келесідей үлгіде анықталады.

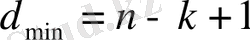(1.1.3)

Барлық t - дағы қателерді құрайтын немесе биттен саны кіші бұрмаланған символдарды түзейтін код келесідей үлгіде көрсетуге болады:

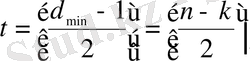(1.1.4)

Бұл теңдіктен t символдық қателіктерді түзейтін Рид-Соломон кодтары 2t - дан көп болмайтын бақылау символдарын талап ететіні көрініп тұр. (1.1.4) тедігінен декодерде п-k "пайдаланылған" артылған символдары бар екенін көруге болады, олардың саны қателерді түзейтін символдардың санынан екі есеге артық болады. Әрбір қате үшін бір артылған символ қатені анықтау үшін қолданылады және біреуі ақиқат мәнін анықтау үшін қолданылады [1]. Өшіруді түзету үшін кодтың мүмкіндігі келесідей үлгіде көрсетіледі.

(1.1.5)

Бір уақытта қателерді түзету және өшіру мүмкіндігін қойылатын талап ретінде көрсетуге болады.

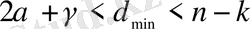(1.1.6)

мұндағы - түзетуге мүмкін болатын қателік символдық комбинцияның саны, ал 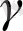- смиволдық өшіру комбинациясының саны, олар түзетілуі мүмкін. Рид-Соломон кодтары сияқты екілік емес кодтардың артықшылығын келесі салыстырулардан көруге болады. (п, k) = (7, 3) екілік кодын қарастырайық. Толықтай n-кортеждер кеңістігі 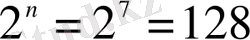n-кортеждер құрайды, ондағы 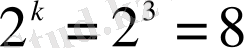(немесе барлық n-кортеждердің 116 бөлігі) кодтық сөздер болып табылады. Одан кейін (n, k)=(7, 3) екілік емес кодты қарастырайық, мұнда әрбір символ т = 3 биттен тұрады. n-кортеждер кеңістігі 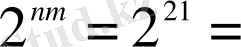2 097 152 n-кортежді құрайды, оның ішінде 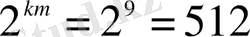(немесе барлық n-кортеждердің 14096 бөлігі) кодтық сөздер болып табылады. Егер операциялар әрбірі т биттен құралған екілік емес символдарға жүргіліп жатса, онда тек маңызды емес мүмкін болатын n-кортеждер бөлігі ( яғни 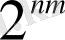үлкен санының 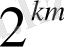) кодтық сөздер болып табылады. Бұл бөлік т өскен сайын кішірейеді. Мұнда маңызды болып табылатыны сол, егер кодтық сөз ретінде n-кортеждер кеңістігінің маңызды емес бөлігі қолданылса, онда үлкен 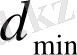алу мүмкін болады [1].
Кез келген сызықтық код n-k символдық өшірудің комбинациясын түзетуге мүмкіндік береді, егер барлық n-k өшірілген символдарды бақылау символдарына келетін болса. Бірақ Рид-Соломон кодтары ерекше қасиетке ие, оның мәні мынада: олар п-k блоктағы өшіру символдарының кез келген жиынтығын түзете алады. Кез келген артық қалған символдарды өзара құрастыруға болады. Артық қалуы өскен сайын оның жоғары жылдамдықты жүзеге асырылу күрделілігі де өседі. Сол себепті Рид-Соломон кодтары жоғары дәрежелі кодтауға ие (артық қалу төмендігі).
Рид-Соломон кодтары үшін қателердің пайда болу ықтималдылығы.
Рид-Соломон кодтары қателер дестесін түзету үшін өте маңызды рөл атқарады, яғни олар жады каналында өте тиімді болып келеді. Сонымен қатар олар үлкен кіріс символдарының жиынтығы каналында жақсы ұсынылған. Рид-Соломон кодының ерекшелігі болып минимальді арақашықтықты өзгертпей n ұзындықты кодқа екі ақпараттық символды қосуға болатыны табылады. Мұндай кеңейтілген код п + 2 ұзындыққа ие және ақиқатты бақылау символдарының саны шығыс коды сияқты болады. Символдық қателердің пайда болу ықтималдылығы:

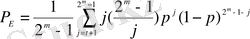(1.1.7)

мұндағы t - символдағы қателік биттерінің саны, олар кодты түзей алады, ал әрбір символдар т биттен тұрады.
Кейбір модуляция типтері үшін биттік қателік ықтималдығын жоғарыдан символдық қателік ықтималдығымен шектеуге болады. М= 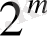мен MFSK ( манипуляцияның бiрнеше жиiлiктерi ) модуляциясы үшін РВ (биттік қателік ықтималдығы) және РЕ арасындағы қатынас келесі формуламен өрнектеледі.

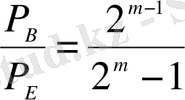(1.1.8)

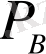-ның p каналдық символда қателіктің пайда болу ықтималдығынан тәуелділігі көрсетілген (сурет 1). Символдағы t қателік биттерін түзету мүмкіндігі және n = 31 (кодтық блоктағы отыз бір 5-биттік символ) бар әр түрлі ортогональді 32- лік Рид-Соломон кодтары үшін (1.1.7) және (1.1.8) теңдіктерінен алынған. 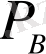Сурет 2.-де MFSK ( манипуляцияның бiрнеше жиiлiктерi ) модуляциясын және AWGN ( аддитивтiк ақ гаустық шумен) каналында когерентті емес демодуляциясын қолданатын кодтау жүйесі үшін - ның 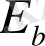N0-дан тәуелділігі көрсетілген.

Сурет 1. Символда t битті түзету мүмкіндігі бар және п = 31 әртүрлі ортогональді 32- лік Рид-Соломон кодтары үшін - ның p-дан тәуелділігі.

Рид-Соломон кодтары үшін қателердің пайда болу ықтималдығы n блоктың ұзындығының өшіруші дәрежелік функциясы болып табылады, ал декодтау күрделілігі блок ұзындығының үлкен емес дәрежесіне пропорционал. Кейде Рид-Соломон кодтары каскадтық жүйелерде қолданылады. Мұндай жүйелерде ішкі өте нақты декодер алдымен демодулятор шығысындағы шешімнің жұмсақ схемасынан туындайтын қателерден кейбір қорғанысты жүзеге асырады; одан кейін өте нақты декодер қатал схема бойынша жасалған деректерді сыртқы Рид-Соломон декодеріне жібереді, ол қателердің пайда болу ықтималдығын азайтады [2].

Сурет 2. Символда t бит түзету мүмкіндігі бар және AWGN каналында 32-лік MFSK модуляциясында п = 31 болатын әр түрлі ортогональді Рид-Соломон кодтары үшін рв - ның EtNQ - дан тәуелділігі.

2 Рид-Соломон кодтарының импулсьті кедергілер кезінде ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.