Математиканың дамуы барысында комплекс

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

КОМПЛЕКС САНДАР ЖӘНЕ ОЛАРДЫҢ ҚОЛДАНЫЛУЫ

МАЗМҰНЫ

КІРІСПЕ . . . 5

І. Математиканың дамуы барысында комплекс

сандардың пайда болу тарихы . . . 6

ІІ. Комплекс сандар және оларға амалдар қолдану.

Комплекс сандардың геометриялық мағынасы

2. 1. Негізгі ұғымдар және комплекс сандарға амалдар қолдану . . . 8

2. 2. Комплекс сандардың геометриялық кескіні.

Тригонометриялық түрі . . . 9

2. 3. Комплекс сандарды дәрежелеу және түбірден шығару . . . 11

2. 4. Алгебралық амалдардың геометриялық мағынасы . . . 12

ІІІ. Комплекс сандардың қолданылуы.

3. 1. Алгебралық теңдеулерді шешу . . . 13

3. 2. Алгебралық тепе-теңдікті дәлелдеу . . . 16

3. 3. Комплекс сандарды тригонометрияда қолдану . . . 17

3. 4. Комплекс сандарды геометрияда қолдану . . . 19

ҚОРЫТЫНДЫ . . . 20

Кіріспе

Алгебралық теңдеулер және оларды шешуге байланысты мәселелер мектеп курсында маңызды мәселелердің бірі болып табылады. Математикада натурал сандар жиынында шешімі болмайтын теңдеулердің шешімін рационал сандар жиынында тауып жатамыз. Сол сияқты кейбір теңдеудің шешімі рационал сандар жиынында табылмай нақты сандар жиынында табылып жатады. Мысалы, х ² =3 теңдеуінің рационал сандар жиынында шешімі жоқ, иирационал сандарды білмеген кезде түбірі жоқ деп жауап беретін болдық. Ал шындығында оның түбірлері бар, түбірлері

\[{\frac{4}{\bot}}{\sqrt{\mathbb{2}}}\]

. Бұл сандарды түсінуге қиын болып көрінгенмен, ұзындығы

\[{\sqrt{3}}\]

-ге тең болатын кесіндінің бар екеніне көзіміз жетті. Сонымен қатар осы иррационал сандардың көмегімен математикалық есептер ғана емес, техниканың, физиканың т. б. есептері оңай шығарылады. Сондықтан сандар ұғымы әрдайым кеңейтіліп отырды. Ал х ² = - 3 теңдеуінің түбірі нақты сандар жиынында жоқ. «Математика неге математикалық операциялар нәтижесінде туындаған теңдеуді шеше алмайды?» деген заңды сауал туындайды. Бұл сұраққа жауап беру үшін сандар өрісін тағы кеңейтуге тура келеді.

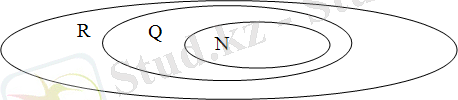N - натурал сандар, Q - рационал сандар, R - нақты сандар, І - комплекс сандар жиыны.

х ² +1=0 квадрат теңдеуін қарастырайық. Бұдан х ² = -1. Яғни берілген теңдеудің түбірі х квадраты -1-ге тең сан болып отыр. Ол санды і жорамал бірлік деп атайды. Сонда і ² = -1, і =

\[\sqrt{-1}\]

. Теңдеудің жауабы х= і.

х ² -8х+25=0 квадрат теңдеуін қарастырайық. Оның түбірлерін былай жазуға болады:

\[x=4\pm{\sqrt{16-25}},\]

\[x=4\pm{\sqrt{9(-1)}},\]

\[x=4\pm3\sqrt{-1},\]

\[x=4\ \pm3i\]

\[4\pm3i\]

түріндегісандар комплекс сандардепаталады. Жалпытүрде а+b i деп жазылады. Мұндағы а, b-нақты сандар, а- комплекс санның нақты бөлігі, b i -комплекс санның жорамал бөлігі, ал b-жорамал бөлігінің коэффициенті деп аталады.

Ол сандар өте ерекше және киын болып көрінгенімен оған нақты сандармен жасалатын амалдар үшін қажетті математикалық білімнен артық білім қажет емес. Осы жұмыста теңдеуді шешуге комплекс сандарының қолданылуына ерекше көңіл бөле отырып, оңай шешу жолы ашып көрсетілген. Сонымен қатар жұмыста қарастырылған тригонометриялық есептерді шешуде комплекс сандарды пайдалану тәсілдерінің тиімділігі өте жақсы көрсетілген.

І ТАРАУ. Математиканың дамуы барысында комплекс сандарының пайда болу тарихы

Ф. Виет Комплекс сандар теріс сандар сияқты математиканың ішкі қажеттілігінен пайда болды нақтырақ айтқанда алгебралық теңдеулерді шешу теориясы мен практикасынан қажеттілігінен туындады. Ең алғаш комплекс сандармен математиктер квадрат теңдеуді шешу кезінде кездесті. ХVI ғасырға дейін дүниежүзі математиктері комплекс сандар ұғымын дұрыс түсіндіре алмай оларды жалған сандар деп қолданбаған. Г. Лейбниц Квадрат теңдеуді шешу тарихы Ежелгі Вавилоннан басталады. Бірақ олар оң түбірлерін ғана таба алған, нақты шешу жолын білмеген. Индус Брахмагупта (VII в. ) квадрат теңдеуді шешудің жалпы әдісін ұсынған. Аль-Хорезми (IX в. ) сызықтық және квадрат теңдеулердің классификациясын жасап, оларды шешу тәсілдерін көрсеткен. Бірақ ол да ноль және теріс түбірлерін қарастырмаған. Квадрат теңдеудің түбірлерінің жалпы формуласын Виет (XVI в. ) қорытып шығарған. Бірақ ол да тек оң түбірлерін ғана тапқан. Тек ХVI ғасырда итальяндық математиктер Тарталья, Кардано, Бомбелли оң түбірлерінен басқа теріс түбірлері бар екендігін ескереді. XVII ғасырда Жирар, Декарт, Ньютон және тағы басқа математиктердің еңбектерінің арқасында квадрат теңдеуді шешудің қазіргі жолы ашылады.

Р. Декарт 3-ші және 4-ші дәрежелі теңдеулерді шешу жолын итальяндық математиктер Тарталья, Кардано және т. б. тапқан. 5-ші және одан да жоғары дәрежелі теңдеулерге байланысты тек ХIX ғасырдың 20-шы жылдары ғана норвегиялық жас математик Нильс Абель бұндай теңдеулердің түбірлері 4 арифметикалық амалдар және түбірден шығарудың көмегімен табу мүмкін еместігін дәлелдеген.

Кардано 3-ші және 4-ші дәрежелі теңдеулермен айналысып жүріп, алғаш рет комплекс сандарды қолдануды ұйғарған. Сонда да олар оған түсініксіз көрінді. Комплекс сандардың мағынасын итальяндық математик Р. Бомбелли түсіндірді.

Комплекс сандар математикада ХVI ғасырда 3-ші дәрежелі алгебралық теңдеулерді шешуге байланысты, кейінірек 2-ші дәрежелі теңдеулерді шешуге байланысты пайда болды. 1545 жылы итальяндық алгебраист Джироломо Кардано табиғаты жаңа сандар енгізуді ұсынды. Ол

\[\frac{{\frac{3}{6}}+\partial=10,}{\left\lfloor x\right\rfloor}\]

теңдеулер жүйесінің нақты сандар жиынында шешімі жоқ, бірақ әрқашан

\[\hat{\hat{\Pi}}\hat{\mathcal{O}}=5\pm\sqrt{-\ 15},\]

шешімі бар. Мұндағы

\[{\sqrt{-{\dot{\boldsymbol{\alpha}}}}}{\sqrt{-{\dot{\boldsymbol{a}}}}}=-a\]

деп алгебраның ережесі бойынша қабылдау қажет екенін айтқан.

1572 жылы итальяндық алгебраист Рафаэль Бомбеллидің осындай сандармен орындалатын амалдардың алғашқы ережелерін жазған кітабы жарық көрді. «Жорамал сандар» деген атауды 1637 жылы француз математигі және философы Рене Декард енгізсе, 1777 жылы VIII ғасырдың атақты математиктерінің бірі Леонард Эйлер і ² =-1 болатын і жорамал бірлігін енгізді.

Комплекс сандар кез-келген квадрат теңдеуді (Д<0 болса да), 3-ші және 4-ші дәрежелі теңдеулерді шешуге мүмкіндік береді. ХVI ғасырдың математиктері ХІХ ғасырдың басына дейін комплекс сандарға сенімсіздікпен қарады. Оларды «жалған», ойдан шығарылған сандар деп атады. Ал Лейбниц бұл сандар «керемет, ғажап» сандар,

\[\sqrt{-1}\]

-ді тосын дүниенің белгісі деп атап, өз зиратына ойып жаздыртуды аманат еткен.

Бірақ бұндай сенімсіздікке қарамастан комплекс сандарды қолдану көптеген қиын мәселелерді шешуге көмектесті. Сондықтан сол заманнан бері комплекс сандардың математикадағы маңызды өте зор. Ең бірінші олар алгебралық теңдеулер теориясына енді.

Комплекс сандардың логикалық қатаң теориясын жасаған ХІХ ғасырда (1835ж) ирландиялық математик Вильям Роу мен Гамильтон болды. Гамильтонның ұйғарымы бойынша комплекс сандар - ол төмендегідей қосу мен көбейту амалдары анықталған z=(x, y) нақты сандар жұбы:

(x ₁ , y ₁ ) + (x ₂ , y ₂ ) =(x ₁ + x ₂ , y ₁ + y ₂ ) ; (1)

(x ₁ , y ₁ ) • (x ₂ , y ₂ ) =(x ₁ x ₂ - y ₁ y ₂ , x ₁ y ₂ + x ₂ y ₁ ) (2)

Мұндағы х және у комплекс санның нақты және жорамал бөлігі деп аталады.

z ₁ =(x ₁ , y ₁ ) және z ₂ =(x ₂ , y ₂ ) екі комплекс сандар тең деп аталады, егер x ₁ =x ₂ , y ₁ = y ₂ болса.

ХІХ ғасырда комплекс сандардың жазықтықтағы нүкте және жазықтықтағы вектор арқылы көрнекті геометриялық кескіні пайда болғаннан кейін жаратылыстанудың, әсіресе гидро-, аэродинамиканың, электротехниканың, геодезия мен картографияның көптеген есептері осы сандардың көмегімен шешім таба бастады. Содан бері комплекс сандар нақты сандар сияқты маңызды бола бастады.

ІІ тарау. Комплекс сандарға алгебралық амалдар қолдану және олардың геометриялық мағынасы

Негізгі ұғымдар және комплекс сандарға арифметикалық амалдар қолдану.

Әрбірнақтысандар комплекс сан депқабылдауғаболады, себебі, 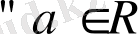үшін

\[a=a+0i\]

Комплекс :

\[R~\propto C\]

z= a+bi және

\[\overline{{\chi}}.\]

= a-bi өзара түйіндессандар депаталады

\[\begin{array}{l}{{1\cdot z+{\overline{{z}}}=2a}}\\ {{2\cdot z\times{\overline{{z}}}=a^{2}+b^{2}=\left|z\right|^{2}}}\\ {{3\cdot{\overline{{z\pm w}}}={\overline{{z}}}\pm w}}\end{array}\]

z ₁ = a+bi жәнеz ₂ = c+di cандарытең

\[\iff\]

\[a=c,\ \ b=d.\]

Комплекс сандарының қосындысы комплекс сан болады.

\[z=z_{1}+z_{2}=(a+b i)+(c+d i)=(a+c)+(b+d).\]

Комплекс сандардың көбейтіндісі комплекс сан.

z=z ₁ ⋅z ₂ =(a+bi) ⋅(c+di) =(ac-bd) +(bc+ad) i.

Комплекс сандарға қолданылатын қосу және көбейту амалдарының қасиеттері:

А) z ₁ +z ₂ = z ₂ +z ₁

Ә) z ₁ z ₂ = z ₂ z ₁ (қосу мен көбейтудің ауыстырымдылық заңы, коммутативтілігі)

Б) z ₁ +(z ₂ + z ₃ ) =(z ₁ + z ₂ ) + z ₃

В) z ₁ (z ₂ z ₃ ) =(z ₁ z ₂ ) z ₃ (қосу мен көбейтудің терімділік заңы, ассоциативтілігі)

Г) (z ₁ + z ₂ ) z ₃ = z ₁ z ₃ + z ₂ z ₃ (үлестірімділік заңы, дистрибутивтілігі)

Комплекс сандардың айырымы мен бөліндісі z+ z ₂ = z ₁ және z z ₂ = z ₁ теңдеулерінің шешімі ретінде табылады.

Комплекс сандардың айырымы комплекс сан.

\[z=z_{1}-z_{2}=\left(a+b i\right)-\,\left(c+d i\right)=\left(a-c\right)+\left(b-d\right);\]

Комплекс сандардың бөліндісі комплекс сан,

\[z_{2}\neq0\]

\[{\frac{z_{1}}{z_{2}}}={\frac{a+b i}{c+d i}}={\frac{\left(a+b i\right)\left(c-d i\right)}{\left(c+d i\right)\left(c+d i\right)\left(c-d i\right)}}={\frac{a c+b d}{c^{2}+d^{2}}}+{\frac{b c-a d}{c^{2}+d^{2}}}i{\frac{d}{d^{2}}}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}+d^{2}).\]

Сонымен, нақтысандар комплекс (b=0) . Олармен нақты сандармен орындағандай барлық амалдарды, түбірден шығаруды да орындай беруге болады. Тек i ² = -1 ескеріп отыру керек.

Комплекс сандардың геометриялық мағынасы және тригонометриялық түрі.

Комплекс сандарды координат жазықтығының көмегімен жазықтықтың нүктелері ретінде өрнектеуге болады. O x - осінің бойына комплекс санның нақты бөлігін (a=a +0∙ i), ал O y осінің бойына оның жорамал бөлігін орналастырсақ ( bi=0+bi) жазықтықта әрбір комплекс сан z( a, b ) нүктесі түрінде анықталады.

\[\triangle O A B\]

тікбұрышты

\[O A=a,\ O B=b,\]

z

\[=A B=r\,\]

r =z=

\[\sqrt{a^{2}+b^{2}}\]

\[{\frac{O A}{A B}}={\frac{a}{r}}=\cos j~{\textrm{p}}~a=r\cos j\]

z= a+bi=r( cosφ+isinφ) - .

\[\left|Z\right|\]

=r - комплекс санныңмодулі

\[(r\geq0)\]

\[\arg z=j\ +2\pi\ell\]

- комплекс санныңаргументі .

Модульдерітең комплекс радиусы сол комплекс .

комплекс өтежеңіл.

Айталық,

z ₁ = r ₁ (cosφ ₁ +isinφ ₁ ),

z ₂ = r ₂ (cosφ ₂ +isinφ ₂ ) болсын.

Онда

\[z_{1}\times z_{2}=r_{1}\rtimes w_{2}\left(\cos(\mathrm{j{\bf\alpha}}_{1}+\mathrm{j{\bf\alpha}}_{2})+i\sin(\mathrm{j{\bf\alpha}}_{1}+\Phi_{2})\right)\]

, яғни комплекс , аргументтеріқосылады. Дәл осы сияқты бөлу амалы орындалады:

\[\frac{z_{1}}{z_{2}}=\frac{r_{1}}{r_{2}}{\left(\cos(j_{\mathrm{\scriptsize~1}}-j_{\mathrm{\scriptsize~2}})+i\sin(j_{\mathrm{\scriptsize~1}}-\phi_{\mathrm{\mathrm{\scriptsize~2}}})\right)}\]

Модудьдерібөлініп, .

\[\left|z_{1}\times c_{2}\right|=r_{1}\cdot r_{2}\]

\[\arg(z_{1}\times z_{2})=\arg z_{1}+\arg z_{2}=\textbf{j}_{1}+\emptyset_{2}\]

Берілген комплекс санды i- ге көбейтудің геометриялық

мағынасы сол санға сәйкес векторды

\[\frac{\pi}{2}\]

-ге бұру

болып табылады.

У z ₁ z ₂ Y

z ₁

z i

z ₂ z

Комплекс сандыдәрежелеу

Егер

\[z=r(\cos{\bf j}\ +i\sin{\phi})\]

болса, (комплекс ) мынадайтеңдікаламыз:

\[\begin{array}{l}{{z^{n}=r^{n}(\cos n j\,\,+i\sin n j\,\,)}}\\ {{\left\vert z^{n}\right\vert=r^{n};\arg z^{n}=n\arg z=n\phi,}}\end{array}\]

\[r^{n}\left(\cos j~+i\sin j~\right)^{n}=r^{n}\mathrm{(cos)}n j~+i\sin n\phi\mathrm{)}\]

яғни комплекс санды дәрежелеу үшін сол көрсеткішке модулін дәрежелеп, ал аргументін көбейтеді.

Бұдан

\[(\cos j~+i\sin j~)^{n}=\cos n j~+i\sin n\phi\]

теңдігі келіп шығады. Бұл - Муавр формуласы деп аталады.

Комплекс саннан n ^ші дәрежелі түбір табу.

Айталық, а=r(cos

\[\frac{\vert\beta\rangle}{\hbar}\]

+isin

\[\frac{g_{0}^{\prime}}{\hbar}\]

) комплекс саны берілсін. Онда жоғарыда қарастырылған көбейту амалының негізінде n- натурал саны үшін

\[a^{n}=\left[r(\cos j\ +i\sin j\ \right])^{n}=r^{n}(\cos n j\ +i\sin n\phi),\]

яғни комплекс санды дәрежелегенде оның модулі сол дәрежеге шығарылады, ал аргументі сол дәреже көрсеткішіне көбейтіледі.

\[a^{\cdot n}=(a^{-1})^{n}\]

теңдігін пайдаланып, Муавр формуласын бүтін теріс сандар үшін де пайдалануға болады.

a=a+bi комплекс санын оң бүтін n дәрежеге шығару үшін Ньютонның биномын пайдаланған орынды, тек

\[i^{4k}=1,\;\;i^{4k+1}=i,\;i^{4k+2}=-\;1,\;\;i^{4k+3}=-\,i\;\;(k\in N)\]

ескерсек жеткілікті.

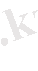
Муавр формуласының дербес түрін қарастырайық.

\[\left(\cos j\,+i\sin\phi\,\right)^{n}=\]

cos n

\[\phi+i\sin n\]

\[{\boldsymbol{\phi}}\,.\]

Теңдіктің оң жақ бөлігіне Ньютонның биномды формуласын қолданайық.

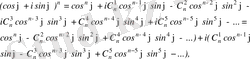
Мұндағы

\[\tilde{N}_{n}^{k}=\frac{n!}{k!(n-k)!}\]

теңдігінің сол және оң жақ бөліктерін салыстырсақ,

\[\begin{array}{l}{{\cos n j\,\,={\cos n}j\,\,-{\cal C}_{n}^{2}\,{\cos}^{n-2}j\,\,\sin^{2}j\,\,+{\cal C}_{n}^{4}\,{\cos}^{n-4}j\,\,\sin^{4}j\,\,-\,...=}}\\ {{\sin\,\,{\left(-1\right)}^{k}{\cos^{n-2}j\,\,{\sin}^{2k}j\,\,}},\,\,}\\ {{\sin n j\,\,{\sin}j\,\,{\sin}^{2k+1}j\,\,{\sin}^{2k}j\,\,\,}}\\ {{\sin{\theta}-{\Omega}^{k}\,{\cos}^{n-1\,2k}j\,\,\,{\sin}^{2k+1}\phi,}}\end{array}\]

теңдіктерін аламыз.

Сонымен,

\[{\sqrt{\hat{\lambda}}}={\frac{n{\hat{\sqrt{r(\cos{\hat{j}}}\ +i\sin{\hat{j}}\mathbf{\hat{n}}})}}{n}}={\check{\nabla}}r(\cos{\frac{j\ +2p k}{n}}+i\sin{\frac{j\ +2\pi k}{n}})\]

, мұндағы

\[k=0,1,...,n-1\]

k -ға әртүрлі мәндер беру арқылы түбірдің әртүрлі мәндерін аламыз.

Қортынды. Комплекс сандардан n - ші дәрежелі түбірді әрқашан табуға болады және оның әртүрлі n мәні болады.

Комплекс сандардың қосындысы мен айырымының векторларға сәйкестігі.

Комплекс санын жазықтықта нүктемен, сонымен қатар координаттар басынан сол нүктеге бағытталған вектормен де кескіндеуге болады. Олай болса комплекс сандардың қосындысы мен айырымын да кескіндеп көрсетуге болады. Оларды қосу векторларды қосудың параллелограмм ережесі бойынша, ал азайту векторларды азайту ережесі бойынша іске асырылады. Сондықтан екі комплекс сандардың қосындысына сәйкес вектор олардың әр қайсысына сәйкес келетін векторлардың қосындысына тең болады. Қысқаша: комплекс сандарды қосу үшін оларға сәйкес векторларды қосу керек. Дәл осы сияқты азайту орындалады.

Y Y

z ₁ z ₁ +z ₂ z ₁

z ₁ -z ₂

z ₂

z ₂ X X

Бұдан

\[\left|z_{1}\right|-\left|z_{2}\right|\Xi\left|z_{1}+z_{2}\right|\Xi\left|z_{1}\right|+\left|z_{2}\right|\]

, ал

\[\left|z_{1}-z_{2}\right|\]

-берілген комплекс сандарға сәйкес нүктелердің ара-қашықтығы.

ІІІ тарау. Комплекс сандардың қолданылуы

Алгебраның негізгі теоремасы

Комплекс сандары туралы мәліметтер алгебралық теңдеулерді шешуге мүмкіндік береді. Мына түрдегі теңдеуді алгебралық теңдеу дейді:

a _n x ⁿ + a _n-1 x ^n-1 + a _n-2 x ^n-2 + . . . + a ₁ x + a ₀ = 0.

Оның сол жағы қандай да бір f(x) көпмүшесі болады, ондағы x - айнымалы, an, a _n-1 , a _n-2 , . . . a ₁ , a ₀ - коэффициенттер (нақты немесе комплекс сандар), n - натурал сан. Егер a _n ≠0 болса, онда n-шідәрежелі теңдеу болады, яғни теңдеудің дәрежесі айнымалының ең үлкен дәрежесіне сәйкес келеді.

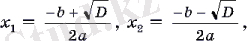
f(x) = 0 теңдеуінің түбірі деп айнымалының орнына қойғанда дұрыс теңдік пайда болатындай қандай да бір t санын айтады. Бірінші дәрежелітеңдеудің ax + b = 0 (a ≠ 0) түбірі no11_01.gif (240 bytes) Сонымен бірге ax ² + bx + c = 0 квадрат теңдеуінің түбірлері төмендегідей формуламен анықталатындығы белгілі:

no11_01.gif (240 bytes)

Мұндағы D = b ² - 4ac - квадрат теңдеудің дискриминанты. Егер D = 0 болса, бұл түбірлер теңеседі.

Жоғарыда x ⁿ - 1 = 0 теңдеуінің шешімі болады және олардың саны теңдеудің дәрежесіне тең болатындығы айтылды. Бұдан мынадай сұрақ туындайды: барлық алгебралық теңдеудің комплекс сандар жиынында шешімі бола ма?

1799 жылы жас неміс математигі К. Гаусс 5-ші және одан жоғары дәрежелі теңдеулердің шешімі болатынын дәлелдеген. Гаусс теоремасында нақты және комплекс санды түбірі бар барлық алгебралық теңдеудің ең болмағанда бір түбірі комплекс сан болатындығы айтылған. Бұл теорема жоғарыда қойылған сұраққа жауап береді және алгебраның негізгі теоремасын дәлелдейді: кез-келген n-ші дәрежелі алгебралық теңдеу n сызықтық теңдеулерге жіктеліп, n түбірі болады.

Бұны мысалдарда қарастырайық. x ⁴ - 4 = 0 теңдеуі берілсін. Бұл теңдеудің сол жағы f(x) =x ⁴ - 1 көпмүшесі. Алгебраның негізгі теоремасы бойынша ол 4 сызықтық көпмүшелерге жіктеледі:

f(x) = (x + 1) (x - 1) (x + i) (x - i) .

Бұл жіктелуді теңдеуге қоятын болсақ: (x + 1) (x - 1) (x + i) (x - i) = 0 теңдеуі шығады. Енді әрбір жақшаны 0-ге теңестіру арқылы 4 түбірін аламыз:

x + 1 = 0, x ₁ = - 1;
x - 1 = 0, x ₂ = 1;
x + i = 0, x ₃ = - i;
x - i = 0, x ₄ = i.

Сонымен бұл теңдеудің дәл 4 түбірі бар.

Комплекс сандардың көмегімен алгебраның негізгі теоремасы бойынша n-й дәрежелі теңдеудің дәл n түбірі болады. Ал біз n-й дәрежелі теңдеудің дәл n немесе одан кем түбірі болады дейтінбіз.

Теріс дискриминатты квадрат теңдеулерді шешу

і ² =-1

екендігін білеміз. Сонымен қатар

(-1) ² =(-1*і) ² =(-1) ² *і ² =-1.

Сонымен, -1-дің квадрат түбірінің кем дегенде екі мәні, атап айтқанда i және -i болады. Мүмкін, квадраты -1 ге тең болатын басқа да комплекс сандар бар шығар?

Бұл мәселенә анықтау үшін а+biкомплекс санының квадраты -1 ге тең деп ұйғарайық. Сонда

(a+di) ² =-1,

a ² +2abi-b ² =-1.

Екі компекс сан, олардың нақты бөліктері және жорамал бөліктерінің

коэффициенттері өз алдында теі болған жағдайда, тек сол жағдайда ғана өзара тең болады. Сондықтан

а ² -b ² =-1,

ab=0. (1)

(1) системасының екінші теңдеуіне сәйкес a мен b сандарының ең болмағанда біреуі нольге тең болуы керек. Егер b=0 болса, онда бірінші теңдеуден a ² =-1 шығады . а-нақты сан, сондықтан

\[{\hat{a}}2\ \ \mathbf{{\hat{a}}}\]

. Теріс емес а ² саны -1 теріс санға тең болуы мүмкін емес. Сондықтан бұл жағдайда b=0 болуы мүмкін емес . Олай болса, а=0 деп қана аламыз, сонда системаның бірінші теңдеуінен шығатыны : -b=-16b=

\[\scriptstyle{\frac{{\frac{\pi}{\mathrm{h}}}}{\mathrm{memensin}}}\]

Демек, квадраты -1 ге тең болатын комплекс сандар : iжәне -i. Олшартты түрде былай жазылады:

\[{\sqrt{-\,1}}=\pm i.\]

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.