Оқушылардың кеңістіктегі елестету қабілеттерін дамытудың психологиялық ерекшеліктері мен сызбалық проекциялау әдістері


Қазақстан Республикасының білім және ғылым министрлігі
КУРСТЫҚ ЖҰМЫС
Тақырыбы:
«Оқушылардың кеңістіктегі елестету қабілеттерін дамытудың психологиялық ерекшеліктері»
Орындаған:
Тексерген:
Орал, 2015ж.
Мазмұны
Кіріспе . . . 3
1. Фигураларды кескіндеудің теориялық негіздемелері
1. 1 Кескіндеу әдістері . . . 6
1. 2 Параллель проекциялау . . . 10
2. Оқушылардың кеңістікте елестету қабілеттерін дамытудың
психологиялық ерекшеліктері
2. 1 Жазықтық фигураларын кеңістікте кескіндеу . . . 15
2. 2 Проекцияда көрінетіндікті анықтау . . . 21
2. 3 Нәрсенің негізгі екі көрінісі бойынша оның үшінші негізгі көрінісін
салу . . . 25
Қорытынды . . . 28
Әдебиеттер . . . 29
Кіріспе
Зерттеу өзектілігі . Сызбаны сабақта қолданудың да өзіндік қиындыктары бар. Себебі екі-өлшемді объектіні кескіндеуге қарағанда, үш өлшемді объектіні кескіндеу принципі басқаша. Егер жазық фигураның кескіні, есеп шартында берілген фигураның қасиеттерін түгел сақтай отырып ұқсастық дәлдігіне дейін бейнелейтін болса, ал кеңістік фигурасының кескінінде түпнұсқаның, яғни есептегі қарастырылып отырған, үш өлшемді фигураның элементтері арасындағы кеністіктік және сандық қатынастары өзгеріске ұшырайды. Жазық фигураны кескіндегенде ешкандай геометриялық проблема тумайды. Сызба түпнұсқаның дәл көшірмесі болады немесе оған ұқсас фигураны береді. Мысалы, сызбадағы дөңгелектің кескінін қарастыра отырып, дөңгелектің өзін көріп отырғандай боламыз.
Кеңістік фигураларын кескіндеу, тіпті басқаша. Өкінішке орай, ұшы ауада із қалдыратындай "кеңістік каламы" болмайды. Мұндай қаламмен қырларын жүргізе отырып кәдімгі кубты салуға болар еді. Ал мұндай қалам болмағандықтан кәдімгі қаламмен кубты қағаз бетіне кескіндеуге тура келеді. Жазық кескін кеңістік фигурасының дәл өзі болуы мүмкін емес. Сол себепті, кеңістік фигурасын қандай ережемен кескіндегенде түпнұсқаны мүмкіндігінше дұрысырақ бейнелейді деген проблема туындайды. Мұндай талаптар екеу; көрнекілік және оңай өлшенімдік.
Нәрсенің берілген негізгі екі көрінісі бойынша оның үшінші негізгі көрінісін салу - сызу пәнінің басты есептерінің бірі. Осындай есептер оқушылардың кеңістікті елестету қабілетін дамытуға әсерін тигізеді. Сондықтан бұл есепті оқушы шығара алатын болуы тиіс. Берілген екі көрініс бойынша үшінші көріністі тұрғызу үшін нәрсенің кеңістіктегі пішінін көз алдымызға елестетіп, түсініп алуымыз керек. Басқаша айтқанда, сызбаны оқи білу керек. Сызбаны оқудың екі әдісі бар. Бұлардың біреуі - талдау әдісі де, екіншісі - толықтыру әдісі. Бұл әдістердің екеуі де геометриялық қарапайым денелердің проекциялары қалай кескінделетінін білуге негізделген.
Нүктенің горизонталь және фронталь проекцияларынан тұратын сызбасы қайтымды болады. Бірақ нәрсенің өзара перпендикуляр екі жазықтықтағы тікбұрышты проекцияларынан тұратын кескін, оның кеңістік бейнесін әрқашан дәл анықтай бермейді. Оның үстіне, іс жүзінде өте күрделі нәрселердің сызбасын сызуда олардың тек екі проекциясы жеткіліксіз болатын жағдайлар көп кездеседі.
Фронталь, горизонталь және профиль проекциялар жазықтықтарының біреуіне де параллель болмайтын кесіндіні жалпы жағдайда орналасқан дейді. Жалпы жағдайда орналасқан кесінді проекцияларының ішінде оське параллель орналасқаны болмайды. Проекциялар жазықтықтарының біріне параллель кесінді деңгейлік кесінді деп аталады. Фронталь проекция жазықтығына параллель кесіндіні фронталь орналасқан кесінді дейді. Фронталь орналасқан кесінді нүктелері π1 жазықтығынан бірдей қашықтықта орналасады. Сызбада фронталь кесіндінің горизонталь проекциясы х осіне, профиль проекциясы z осіне параллель орналасады, ал фронталь проекциясының ұзындығы кесіндінің өзіне тең. Горизонталь проекциялар жазықтығына параллель орналасқан кесіндіні горизонталь орналасқан кесінді дейді. Горизонталь кесінді нүктелері горизонталь проекциялар жазықтығынан бірдей қашықтықта орналасады. Сызбада горизонталь кесіндінің фронталь проекциясы х осіне, профиль проекциясы у осіне параллель орналасады, ал оның горизонталь проекциясының ұзындығы өзінің ұзындығына тең болады. π3 жазықтығына параллель кесінді профиль орналасқан кесінді деп аталады. Профиль кесіндінің горизонталь проекциясы у осіне, фронталь проекциясы z осіне параллель орналасады, ал оның ұзындығы профиль проекцияда сақталады.
Зерттеу жұмысының мақсаты : Негізгі көріністер мен қосымша көріністер шығарып алуға, сызбада көріністерді орналастыруға үйрету. Тетік бөлшектің берілген негізгі екі көрінісі бойынша үшінші негізгі көрінісін салуға, кеңістікте зерттеуге дағдыландыру.
Зерттеу жұмысының міндеттері:
- Оқушыларды теориядан сарамандылық жұмысқа икемдеу, оқушылардың ой-өрісін, білімін, шығармашылыққабілетін, сабаққа деген қызығушылығын, шеберлігін дамытуға арналған әдістер;
- Кеңістік ой өрісін кеңейтуге арналған тапсырмалар, әдістер.
- оқушыларды сызбаны орындау барысында қолданылатын шарттылықтармен және ықшамдаулармен таныстыру.
Зерттеу жұмысының құрылымы: кіріспелен, екі бөлімнен және қорытынды мен пайдаланылған әдебиеттер тізімінен тұрады.
1. Фигураларды кескіндеудің теориялық негіздемелері
1. 1 Кескіндеу әдістері.
1 Е
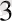 евклидтік кеңістікті меншіксіз элементтермен
евклидтік кеңістікті меншіксіз элементтермен
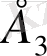 кеңейтілген кеңістігіне дейін толықтырайық. Е
кеңейтілген кеңістігіне дейін толықтырайық. Е
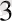 кеңістігіндегі қайсыбір α жазықтығын, F' фигурасын және SS
кеңістігіндегі қайсыбір α жазықтығын, F' фигурасын және SS
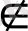 α пен S
α пен S
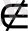 F' нүктесін алайық. π(M') =Mₒ=SM'∩α,
F' нүктесін алайық. π(M') =Mₒ=SM'∩α,
 М
М
 F' заңы бойынша
F' заңы бойынша
π:F'→α
бейнелеуін S центрінен α жазықтығына F' фигурасын проекциялау деп атайды. α жазықтығын проекциялар жазықтығы (немесе кескіндер жазықтығы), F'- түпнұсқа, πF'=Fₒ-α жазықтығындағы F' түпнұсқасының проекциясы деп аталады.
 Әдетте проекциялар жазықтығы ретінде парақ қағаз жазықтығын алуға болады. Fₒ- шектеулі диаметрлі фигура проекциясы парақ қағаз жазықтығына сыймаған жағдайда да осылай алынады. Сондықтан α жазықтығындағы F' түпнұсқасының Fₒ проекциясын алып, парақ қағазда, р(Fₒ) =F фигурасының орналасуы мен өлшемдері жағынан бізге ыңғайлы болатындай, α жазықтығын р ұқсастық түрлендіруіне ұшыратамыз. F фигурасы F' түпнұсқасының кескіні деп аталады [1] .
Әдетте проекциялар жазықтығы ретінде парақ қағаз жазықтығын алуға болады. Fₒ- шектеулі диаметрлі фигура проекциясы парақ қағаз жазықтығына сыймаған жағдайда да осылай алынады. Сондықтан α жазықтығындағы F' түпнұсқасының Fₒ проекциясын алып, парақ қағазда, р(Fₒ) =F фигурасының орналасуы мен өлшемдері жағынан бізге ыңғайлы болатындай, α жазықтығын р ұқсастық түрлендіруіне ұшыратамыз. F фигурасы F' түпнұсқасының кескіні деп аталады [1] .
Кейде р ұқсастық түрлендіруінің қажеттігі болмаған жағдайда р =e (e-α жазықтығын теңбе- тең түрлендіру) деп аталады. Осы жағдайда F=Fₒ, яғни түпнұсқа кескініне оның проекциясы алынады.
F' жазықтық болып келген маңызды, дербес жағдайды қарастырайық. Атап айтқанда, екі α', α'ₒ

 жазықтығы мен S'S'
жазықтығы мен S'S'
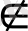 α', S'
α', S'
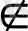 α'ₒ нүктесін алайық. S' центрінен α' жазықтығын α'ₒ жазықтығына π
α'ₒ нүктесін алайық. S' центрінен α' жазықтығын α'ₒ жазықтығына π
 проекциялау кез келген а'
проекциялау кез келген а'
 α' түзуін а'ₒ
α' түзуін а'ₒ
 α'ₒ түзуіне көшіретін
α'ₒ түзуіне көшіретін
π
 :α'→α'ₒ
:α'→α'ₒ
биективтік бейнелеу болып табылады (2сурет) . Демек, бұл проективтік бейнелеу болады. Бірақ бұл α' жазықтығының α'ₒ жазықтығына жалпы жағдайдағы проективтік бейнелеуі бола алмайды, өйткені қарастырылып отырылған жағдайдағы сәйкес бейнелеуде қос нүктені қосатын барлық M'M'ₒ түзулері S' центрі бар түзулер байламына жатады. Осындай қасиеті бар α'→α'ₒ бейнелеуі перспективтік бейнелеу деп аталады. (Бұл жазықтықты жазықтыққа проективтік бейнелеудің дербес жағдайы екеін көреміз. Бұл жағдайда кеңейтілген жазықтық алынатынын ескертеміз!) а' пен а'ₒ түзулерінің А' қиылысу нүктесі s'=α'∩α'ₒ түзуінде жататыны анық. [2]
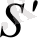 F'{S', α', α'ₒ} фигурасын, α жазықтығын және SₒSₒ
F'{S', α', α'ₒ} фигурасын, α жазықтығын және SₒSₒ
 α мен Sₒ
α мен Sₒ
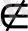 F' нүктесін алып, Sₒ центрінен алынған F' фигурасын α жазықтығына π:F'→α проекциялауды қарастырайық. Айталық π(S') =S, π(s') =s болсын. Жоғарыда айтылғаннан; π бейнелеуінің тарылуы
F' нүктесін алып, Sₒ центрінен алынған F' фигурасын α жазықтығына π:F'→α проекциялауды қарастырайық. Айталық π(S') =S, π(s') =s болсын. Жоғарыда айтылғаннан; π бейнелеуінің тарылуы
πα':α'→α және πα':α'ₒ→α
проективтік бейнелеу болатындығы шығады. Сондықтан бейнелеу көбейтіндісі (компазициясы)
(πα'ₒ) ·π
 ·(πα')
·(πα')
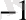 = f
= f
α жазықтығының проективтік түрлендіруі болып табылады. [3]
Біздер, егер π
 (M') =M'ₒ, π(M') =M және π(M'ₒ) =Mₒ болса, онда f(M) =Mₒ болатындығын көреміз. Мұнан кез келген А
(M') =M'ₒ, π(M') =M және π(M'ₒ) =Mₒ болса, онда f(M) =Mₒ болатындығын көреміз. Мұнан кез келген А
 s нүктесі f түрлендіруінде қозғалмайтындығы, ендеше, f- осі s болып келген гомология екендігі шығады. S- гомология центрі екенін байқау киын емес. Шынында да, (M'M'ₒ) түзуі S' нүктесінен өтеді. Жалпы жағдайда π проекциялауында бұл түзу S=π(S') нүктесінен өтетін MMₒ түзуіне көшеді. [4]
s нүктесі f түрлендіруінде қозғалмайтындығы, ендеше, f- осі s болып келген гомология екендігі шығады. S- гомология центрі екенін байқау киын емес. Шынында да, (M'M'ₒ) түзуі S' нүктесінен өтеді. Жалпы жағдайда π проекциялауында бұл түзу S=π(S') нүктесінен өтетін MMₒ түзуіне көшеді. [4]
Сонымен, М, Mₒ=f(M) қос нүктесін қосатын әрбір түзу π(S) шоғына тиісті, сондықтан S- f гомологиясының центрі. α'ₒ жазықтығын негізгі жазықтық, π
 проекциялауын - ішкі проекциялау, π- сыртқы проекциялау, M'ₒ(M' нүктесінің ішкі проекциясы) - M' нүктесінің негізі деп атайды. Жоғарыда алынған нәтижені осы терминдерде былай тұжырымдауға болады:
проекциялауын - ішкі проекциялау, π- сыртқы проекциялау, M'ₒ(M' нүктесінің ішкі проекциясы) - M' нүктесінің негізі деп атайды. Жоғарыда алынған нәтижені осы терминдерде былай тұжырымдауға болады:
Т е о р е м а. π сыртқы проекциялауы α кескіндеу жазықтығында кез келген M'
 α' нүктесінің М проекциясын оның М'ₒ
α' нүктесінің М проекциясын оның М'ₒ
 α'ₒ негізінің Mₒ проекциясына көшіретін f гомологиясын орнатады. s=π(α'∩α'ₒ) түзуі f гомологиясының осі, ал центрі πS' нүктесі болады, мұндағы S'- ішкі проекциялау центрі.
α'ₒ негізінің Mₒ проекциясына көшіретін f гомологиясын орнатады. s=π(α'∩α'ₒ) түзуі f гомологиясының осі, ал центрі πS' нүктесі болады, мұндағы S'- ішкі проекциялау центрі.
Ұқсастық түрлендіру нүктелер мен түзулердің тиістілік қатынасын сақтайды және сондықтан да M'
 α' нүктелерінің кескіндері мен олардың М'ₒ
α' нүктелерінің кескіндері мен олардың М'ₒ
 α'ₒ негіздерінің кескіндері үшін теоремада көрсетілген тәуелділікті сақтайды. [5]
α'ₒ негіздерінің кескіндері үшін теоремада көрсетілген тәуелділікті сақтайды. [5]
2 Айталық, π:F'→ α - S центрінен проекциялау болсын. Егер S меншікті нүкте болса, онда π проекциялауы центрлік проекциялау, ал егер S центрі меншіксіз нүкте болса, онда проекциялау параллель проекциялау (барлық (SM') проекциялаушы түзулері параллель түзулердің байламына жататын болады) деп аталады.
F' фигурасының F кескіндерін мақсатына қарай оны не центрлік не параллель проекциялау көмегімен орындайды. Педагогикалық процестерде қолданылатын кескіндерге мынадай талаптар қойылады:
F кескіні сенімді болуы тиіс, яғни түпнұсқаның кейбір проекциясына ұқсас болуы тиіс;
Ол көрнекі болуы тиіс (түпнұсқаның кеңістіктегі елестеуін тудыруы керек) ;
Ол еркін орындалатындай болуы тиіс (оны орындағанда оқытылып отырылған тақырыпқа қатысы жоқ басқа бір салулар қолданылмауы тиіс) .
Параллель преоекциялау көмегімен орындалған кескіндер сенімді, әрі жеткілікті түрде көрнекі бола алады. Мұндай кескіндерді салу центрлік проекциялау көмегімен салынатын кескіндерге қарағанда әлдеқайда жеңіл. Сондықтан геометрияны мектепте оқытуда түпнұсқадан параллель проекциялау арқылы алынған фигураның кескіндері қолданылады.
1. 2 Параллель проекциялау
Айталық π - S центрінен Ʃ жазықтығына F' фигурасының параллель проекциялауы болсын. Е
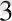 кеңістігінде S
кеңістігінде S
 Е
Е
 меншіксіз нүктесі бағытты, яғни параллель түзулер байламын анықтайды. Бұл бағыт ( сондықтанда да S нүктесін де ) қандай да бір t меншікті түзуінің берілуімен бір мәнді анықталады. π проекциялауы t бағыты бойынша өтеді деп айтады.
меншіксіз нүктесі бағытты, яғни параллель түзулер байламын анықтайды. Бұл бағыт ( сондықтанда да S нүктесін де ) қандай да бір t меншікті түзуінің берілуімен бір мәнді анықталады. π проекциялауы t бағыты бойынша өтеді деп айтады.
F' - кейбір Ʃ' жазықтығы болып келген жағдайды қарастырайық. Проекциялау бағытын анықтайтын t түзуі Ʃ, Ʃ'
 Е
Е
 жазықтықтарын ың әрбіреуімен қиылысатын болсын деп алдын ала ұйғаралық. Сонда t бағыты бойынша π проекциялауы
жазықтықтарын ың әрбіреуімен қиылысатын болсын деп алдын ала ұйғаралық. Сонда t бағыты бойынша π проекциялауы
π: Ʃ'→ Ʃ
биективті бейнелеуін анықтайды. a'
 Ʃ' түзуін алайық. a' түзуінің A', B', C', . . . нүктелерін проекциялаушы түзулердің барлығы бір П жазықтығында жатады. a= П
Ʃ' түзуін алайық. a' түзуінің A', B', C', . . . нүктелерін проекциялаушы түзулердің барлығы бір П жазықтығында жатады. a= П
 Ʃ түзуі Ʃ жазықтығындағы a' түзуінің проекциясы болып табылады
Ʃ түзуі Ʃ жазықтығындағы a' түзуінің проекциясы болып табылады
 жазықтығының a' және а түзулері (AA'), (BB'), (CC') параллель түзулерімен қиылған. Бұдан (A'B', C') =(AB, C) . [7]
жазықтығының a' және а түзулері (AA'), (BB'), (CC') параллель түзулерімен қиылған. Бұдан (A'B', C') =(AB, C) . [7]
Сонымен π: Ʃ'→ Ʃ параллель проекциялауы үш нүктенің қатынасын сақтайды. Демек, π― Ʃ жазықтығына Ʃ' жазықтығының аффиндік бейнелеуі болады. Бірақ Ʃ- ға Ʃ' жазықтығының аффиндік бейнелеуінің жалпы жағдайы бола алм
 айды, өйткені сәйкестенуші нүктелерді қосатын барлық түзулердің әрбіреуі параллель түзулердің байламына тиісті. Мұндай бейнелеу перспективті - аффиндік бейнелеу деп аталады.
айды, өйткені сәйкестенуші нүктелерді қосатын барлық түзулердің әрбіреуі параллель түзулердің байламына тиісті. Мұндай бейнелеу перспективті - аффиндік бейнелеу деп аталады.
Егер Ʃ' жазықтығында екі a' және b' параллель түзулерін алсақ, онда Ʃ жазықтығындағы олардың проекциялары - а мен b түзулері параллель болатынын (жазықтықты жазықтыққа кез келген аффиндік бейнелеуде параллель түзулер - параллель түзуге көшеді) ескерте кетеміз. [8]
2 Теореманы параллель проекциялау жағдайына қолданайық. Ішкі және сыртқы проекциялау мен Ʃ', Ʃ
 Ē
Ē
 жазықтықтарының өзара орналасуының сипаттарына қарай, мына дербес жағдайларды айыра білу керек (3-сурет) .
жазықтықтарының өзара орналасуының сипаттарына қарай, мына дербес жағдайларды айыра білу керек (3-сурет) .
 1. π
1. π
 мен π - параллель проекциялау (S' пен S
мен π - параллель проекциялау (S' пен S
 меншіксіз нүктелер), s' = Ʃ' ∩ Ʃ
меншіксіз нүктелер), s' = Ʃ' ∩ Ʃ
 ' түзуі меншікті түзу ( алайда s' түзуі мен π
' түзуі меншікті түзу ( алайда s' түзуі мен π
 және π проекциялауларының бағыттары компланар емес) . Кескіндер жазықтығында алатынымыз: π(s') = s түзуі - меншікті түзу, π(S') =S нүктесі - меншіксіз нүкте ( өйткені S= (S' S
және π проекциялауларының бағыттары компланар емес) . Кескіндер жазықтығында алатынымыз: π(s') = s түзуі - меншікті түзу, π(S') =S нүктесі - меншіксіз нүкте ( өйткені S= (S' S
 ) ∩Ʃ, ал (S' S
) ∩Ʃ, ал (S' S
 ) түзуі меншіксіз түзу) әрі S≠s. Демек теоремада айтылган f гомологиясы бұл жерде М'=Ʃ' нүктесінің М проекциясын оның М
) түзуі меншіксіз түзу) әрі S≠s. Демек теоремада айтылган f гомологиясы бұл жерде М'=Ʃ' нүктесінің М проекциясын оның М
 '
'
 Ʃ
Ʃ
 ' табанының М
' табанының М
 проекциясына көшіретін s осімен тектес және (ММ
проекциясына көшіретін s осімен тектес және (ММ
 ) тектестігінің бағыты болады. [9]
) тектестігінің бағыты болады. [9]
 2 π
2 π
 - центірлік, π - параллель проекциялаулар Ʃ'‖ Ʃ
- центірлік, π - параллель проекциялаулар Ʃ'‖ Ʃ
 '. Бұл жағдайда f гомологиясының меншікті S центрі және меншіксіз s осі болады, сондықтан да S центрі бар және k
'. Бұл жағдайда f гомологиясының меншікті S центрі және меншіксіз s осі болады, сондықтан да S центрі бар және k
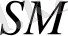
 = k
= k
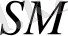
 коеффицентті геометрия болып табылады (4-сурет) .
коеффицентті геометрия болып табылады (4-сурет) .
π - параллель проекциялауы түзудегі үш нүктенің қатынасын сақтайтындығын ескеріп,
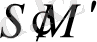
 = k
= k
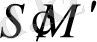 шартынан k - ны анықтауға болады.
шартынан k - ны анықтауға болады.
 3 π
3 π
 мен π - параллель проекциялаулар Ʃ'‖ Ʃ
мен π - параллель проекциялаулар Ʃ'‖ Ʃ
 '. f гомологиясының Ʃ жазықтығында S меншіксіз центрі мен s меншіксіз осі болады және олай болса,
'. f гомологиясының Ʃ жазықтығында S меншіксіз центрі мен s меншіксіз осі болады және олай болса,
 векторымен анықталатын параллель көшіру болып табылады (5-сурет) .
векторымен анықталатын параллель көшіру болып табылады (5-сурет) .
f гомологиясының қарастырылған жағдайы кескіндерді салу барысында жиі ұшырасады. Басқаша жағдайда S' пен S
 нүктелерін және Ʃ' пен Ʃ
нүктелерін және Ʃ' пен Ʃ
 ' жазықтықтарының өзара орналасуын таңдауда жалпылама теоремасымен пайдалану керек [10] .
' жазықтықтарының өзара орналасуын таңдауда жалпылама теоремасымен пайдалану керек [10] .
Параллель проекциялау. Проекциялау центрі өзіндік емес нүкте болатын центрлік проекцияның жеке түрін параллель проекция деп атайды. Өзіндік емес нүкте өзіндік түзудің көмегімен анықталатындықтан проекциялау аппараты бұл жағдайда проекциялар жазықтығынан және шексіз қашықтықта жатқан S
 нүктесі арқылы өтетін, проекциялау бағыты деп аталатын s түзуінен тұрады. Берілген А нүктесінің кескінін салу үшін А нүктесі арқылы s түзуіне параллель
нүктесі арқылы өтетін, проекциялау бағыты деп аталатын s түзуінен тұрады. Берілген А нүктесінің кескінін салу үшін А нүктесі арқылы s түзуіне параллель
 ɑ түзуін жүргізеді. Осы ɑ түзуі мен проекциялар жазықтығының қиылысу нүктесі Аʹ іздеп отырған кескініміз болады. Проекциялау бағыты проекциялар жазықтығына параллель болмауы тиіс (s≠π') . Бізге өзара параллель ɑ және в түзулері беріліп, олардың кескіндерін салу керек болсын. Ол үшін а түзуі бойынан А нүктесін және в түзуі бойынан В нүктесін алып, осы А және В нүктелері арқылы s түзуіне параллель m және n түзулерін жүргіземіз. Сонда қиылысатын a және m түзулері α жазықтығынан, ал в және n түзулері β жазықтығынан анықтайды. α жазықтығы мен π' жазықтығының қиылысу сызығын а' деп белгілеп, оны а түзуінің кескіні ретінде қарастырамыз. Сол сияқты в' түзуі (в'=∩π') в түзуінің кескіні болады. Табылған А' нүктесін А нүктесінің π' жазықтығындағы s бағытындағы параллель проекциясы деп атайды. Нәрсенің кескінін осылайша табуды параллель проекциялау дейді. Параллель проекциялауда да нүкте нүктеге, проекциялау бағытына параллель емес түзу түзуге проекцияланады және өзара меншіктілік сақталады. [11]
ɑ түзуін жүргізеді. Осы ɑ түзуі мен проекциялар жазықтығының қиылысу нүктесі Аʹ іздеп отырған кескініміз болады. Проекциялау бағыты проекциялар жазықтығына параллель болмауы тиіс (s≠π') . Бізге өзара параллель ɑ және в түзулері беріліп, олардың кескіндерін салу керек болсын. Ол үшін а түзуі бойынан А нүктесін және в түзуі бойынан В нүктесін алып, осы А және В нүктелері арқылы s түзуіне параллель m және n түзулерін жүргіземіз. Сонда қиылысатын a және m түзулері α жазықтығынан, ал в және n түзулері β жазықтығынан анықтайды. α жазықтығы мен π' жазықтығының қиылысу сызығын а' деп белгілеп, оны а түзуінің кескіні ретінде қарастырамыз. Сол сияқты в' түзуі (в'=∩π') в түзуінің кескіні болады. Табылған А' нүктесін А нүктесінің π' жазықтығындағы s бағытындағы параллель проекциясы деп атайды. Нәрсенің кескінін осылайша табуды параллель проекциялау дейді. Параллель проекциялауда да нүкте нүктеге, проекциялау бағытына параллель емес түзу түзуге проекцияланады және өзара меншіктілік сақталады. [11]
Проекциялау бағытына параллель түзулер проекциялаушы түзулер деп аталады. Проекциялаушы түзулер нүктелерге кескінделеді (проекцияланады) .
Берілген түзудің проекциясын салу үшін сол түзу арқылы проекциялық бағытына параллель жазықтық жүргізіледі. Жоғарыда а түзуінің проекциясын табу үшін осы а түзуі арқылы s түзуіне (проекциялау бағытына) параллель α жазықтығы, ал в түзуін проекциялау үшін -β жазықтығы жүргізілді. Аталған α және β жазықтықтарын проекциялаушы жазықтықтар деп атайды. Жалпы алғанда проекциялаушы жазықтық деп проекциялау бағытына параллель жазықтықты айтады. Проекциялаушы жазықтық түзуге проекцияланады. [9] Параллель түзулердің параллель проекциялары параллель болады. Егер а‖в болса, онда а'‖в' болады. Бұл айтылғанды дәлелдейік. Ол үшін а және в түзулері параллель екен деп ұйғаралық. Олай болса оларды проекциялайтын α және β жазықтықтары да өзара параллель болады. Өйткені α жазықтығының қиылысатын екі түзуі (а мен m) β жазықтығының қиылысатын екі түзуіне параллель. Жоғарыда m және n түзулерін s түзуіне параллель
 етіп жүргіздік. Сондықтан m‖n болады. Өзара параллель екі жазықтықты үшінші бір жазықтықпен қиғанда пайда болатын екі түзу де өзара параллель болады. α‖β; α∩π'=а'; β∩π'=в', олай болса, а'‖в' болады. [7]
етіп жүргіздік. Сондықтан m‖n болады. Өзара параллель екі жазықтықты үшінші бір жазықтықпен қиғанда пайда болатын екі түзу де өзара параллель болады. α‖β; α∩π'=а'; β∩π'=в', олай болса, а'‖в' болады. [7]
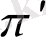 Өзара параллель АВ және CD кесінділерін алып, оларды π' жазықтығына s бағытында проекциялайық. Сонда АВ кесіндісі А'В' кесіндісіне, ал CD кесіндісі C'D' кесіндісіне проекцияланады және (А'В') ‖( C'D') болады. А нүктесі арқылы А'В' -қа параллель етіп жүргізілген түзу ВВ'-ты Е нүктесінде, ал D нүктесі арқылы C'D'-қа параллель етіп жүргізілген түзу СС'-ты F нүктесінде қияды. Сонда пайда болған үшбұрыштар AEB және DFC өзара ұқсас үшбұрыштар болады. Өйткені
Өзара параллель АВ және CD кесінділерін алып, оларды π' жазықтығына s бағытында проекциялайық. Сонда АВ кесіндісі А'В' кесіндісіне, ал CD кесіндісі C'D' кесіндісіне проекцияланады және (А'В') ‖( C'D') болады. А нүктесі арқылы А'В' -қа параллель етіп жүргізілген түзу ВВ'-ты Е нүктесінде, ал D нүктесі арқылы C'D'-қа параллель етіп жүргізілген түзу СС'-ты F нүктесінде қияды. Сонда пайда болған үшбұрыштар AEB және DFC өзара ұқсас үшбұрыштар болады. Өйткені
 ВАЕ=
ВАЕ=
 CDF және
CDF және
 АВЕ=
АВЕ=
 DCF болатынын дәлелдеу қиын емес. Осы екі үшбұрыштың ұқсастығынан
DCF болатынын дәлелдеу қиын емес. Осы екі үшбұрыштың ұқсастығынан
 /
/
 =
=
 /
/
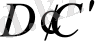 теңдігін аламыз. Яғни параллель кесінділер проекцияларының қатынасы сол кесінділердің өздерінің қатынасына тең болады екен. Енді CD кесіндісін АВ кесіндісіне біртіндеп жақындата берелік. Сөйтіп, оларды А=D болатындай етіп беттестірелік. Сонда бір түзудің бойында жататын екі кесінді аламыз. Олай болса, параллель проекциялау кезінде бір түзудің бойында орналасқан кесінділердің де қатынастары сақталады екен. Бұдан біз маңызды қорытынды аламыз: түзуді берілген қатынаста бөлудің орнына оның кескінін берілген қатынаста бөлуге болады. Мысалы, К нүктесінің проекциясы К' берілген MN кесіндісі проекциясының, яғни M'N' кесіндісінің ортасы болады. [11]
теңдігін аламыз. Яғни параллель кесінділер проекцияларының қатынасы сол кесінділердің өздерінің қатынасына тең болады екен. Енді CD кесіндісін АВ кесіндісіне біртіндеп жақындата берелік. Сөйтіп, оларды А=D болатындай етіп беттестірелік. Сонда бір түзудің бойында жататын екі кесінді аламыз. Олай болса, параллель проекциялау кезінде бір түзудің бойында орналасқан кесінділердің де қатынастары сақталады екен. Бұдан біз маңызды қорытынды аламыз: түзуді берілген қатынаста бөлудің орнына оның кескінін берілген қатынаста бөлуге болады. Мысалы, К нүктесінің проекциясы К' берілген MN кесіндісі проекциясының, яғни M'N' кесіндісінің ортасы болады. [11]
Проекциялар жазықтығына параллель α жазықтығында жатқан АВС үшбұрышының параллель проекциясын қарастыралық. А'В'С' үшбұрышы проекциялар жазықтығына параллель АВС үшбұрышының параллель проекциясы болсын (α‖π') . Сонда АВВ'А' төртбұрышы паралеллограмм екенін көреміз. Паралеллограмнің қарама-қарсы қабырғалары өзара тең болатынын білеміз. Сондықтан
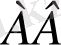 =
=
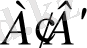 болады. Олай болса, проекциялар жазықтығына параллель кесінді өзінің ұзындығын (натурал шамасын) сақтап проекцияланады екен:
болады. Олай болса, проекциялар жазықтығына параллель кесінді өзінің ұзындығын (натурал шамасын) сақтап проекцияланады екен:
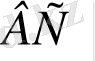 =
=
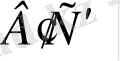 және
және
 =
=
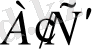 . Бұдан ∆АВС=∆А'В'С' болатынын көреміз. Проекциялар жазықтығына параллель жазық фигураның параллель проекциясы сол фигураның өзіне тең болады.
. Бұдан ∆АВС=∆А'В'С' болатынын көреміз. Проекциялар жазықтығына параллель жазық фигураның параллель проекциясы сол фигураның өзіне тең болады.
Осы жасалған тұжырымдардан параллель проекциялаудың мынадай қасиеттері алынады:
1 Қандай да бір сызыққа тиісті нүктенің проекциясы осы сызыктын проекциясына тиісті болады.
2 Түзудің проекциясы түзу болады.
3 Параллель түзулердің проекциялары да параллель болады.
4 Проекциялауда бір түзудің немесе параллель түзулердің бойында жатқан кесінділердің қатынасы сақталады [12] .
2. Оқушылардың кеңістікте елестету қабілеттерін дамытудың психологиялық ерекшеліктері
2. 1 Жазықтық фигураларын кеңістікте кескіндеу
Айталық Ʃ' жазықтығында A' B'C' үшбұрышы берілсін. (A'B') түзуі арқылы Ʃ≠Ʃ' жазықтығын жүргізейік те Ʃ жазықтығынан қандай да бір MNP үшбұрышын алайық. Ʃ жазықтығында [A'B'] қабырғасына A' B'C'
 MNP үшбұрышын алайық. Егер A' B'C' үшбұрышын Ʃ жазықтығына (С'C) бағыты бойынша проекцияласақ, онда A' B'C' үшбұрышын аламыз (MNP үшбұрышына ұқсас ) .
MNP үшбұрышын алайық. Егер A' B'C' үшбұрышын Ʃ жазықтығына (С'C) бағыты бойынша проекцияласақ, онда A' B'C' үшбұрышын аламыз (MNP үшбұрышына ұқсас ) .
Сонымен, алдын ала берілген кез келген үшбұрышқа ұқсас үшбұрыш - берілген А'В'С' үшбұрышының параллель проекциясы бола алады. Мұнан, кез келген MNP үшбұрышының берілген А'В'С' үшбұрышының кескіні бола алатындығы шығады.
Егер Σ кескіндер жазықтығында проекциялау бағыты Σ' жазықтығына параллель емес параллель проекциялау көмегі арқылы алынған жалпы жағдайдағы Σ' жазықтығының қандайда болса үш нүктесінің кескіндері көрсетілсе, онда Σ' жазықтығының әрбір нүктесінің кескінін салуға болады.
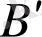 Айталық, А
Айталық, А
 , В
, В
 , С
, С

 Σ нүктелері жалпы жағдайдағы А'В'С'
Σ нүктелері жалпы жағдайдағы А'В'С'
 Σ' нүктелерінің параллель проекциялары болсын делік. проекциялау бағыты Σ' жазықтығына параллель болмағандықтан, А
Σ' нүктелерінің параллель проекциялары болсын делік. проекциялау бағыты Σ' жазықтығына параллель болмағандықтан, А
 , В
, В
 , С
, С
 нүктелері бір түзудің бойында жатпайды. Қалауымызша М'
нүктелері бір түзудің бойында жатпайды. Қалауымызша М'
 Σ' нүктесін алайық. Айталық, N'=(A'M') ∩(B'C') . N' пен M' нүктелері Nₒ, Mₒ
Σ' нүктесін алайық. Айталық, N'=(A'M') ∩(B'C') . N' пен M' нүктелері Nₒ, Mₒ
 Σ нүктелеріне проекцияланса, (BₒCₒ, Nₒ) =(B'C', N'), (AₒNₒ, Mₒ) =(A'N', M') болады. [16]
Σ нүктелеріне проекцияланса, (BₒCₒ, Nₒ) =(B'C', N'), (AₒNₒ, Mₒ) =(A'N', M') болады. [16]
Айталық, АВС
 Σ үшбұрышы А'В'С' үшбұрышының кескіні болып табылсын. (Сондықтанда, ∆ABC
Σ үшбұрышы А'В'С' үшбұрышының кескіні болып табылсын. (Сондықтанда, ∆ABC
 ∆AₒBₒCₒ) . ∆AₒBₒCₒ үшбұрышын ∆ABC үшбұрышына көшіретін ρ ұқсастығы Nₒ мен Mₒ нүктелерін (BC, N) =(BₒCₒ, Nₒ), (AN, M) =(AₒNₒ, Mₒ) орындалатын N мен M нүктелеріне көшіреді.
∆AₒBₒCₒ) . ∆AₒBₒCₒ үшбұрышын ∆ABC үшбұрышына көшіретін ρ ұқсастығы Nₒ мен Mₒ нүктелерін (BC, N) =(BₒCₒ, Nₒ), (AN, M) =(AₒNₒ, Mₒ) орындалатын N мен M нүктелеріне көшіреді.
Сондықтан да, (BC, N) = (B'C', N'), (AN, M) = (A'N', M') .
Осы екі теңдіктің оң жақ бөліктері белгілі. Осы теңдіктерді пайдаланып, біз алдымен N
 (ВС) нүктесін, осыдан кейін M
(ВС) нүктесін, осыдан кейін M
 (AN) нүктесін саламыз. Сонда М нүктесі М' нүктесінің кескіні болып табылады.
(AN) нүктесін саламыз. Сонда М нүктесі М' нүктесінің кескіні болып табылады.
Төртбұрыштың кескінін салу
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz