Орта мектепте геометрияны оқытуда жазықтықтағы салу есептері арқылы оқушылардың конструктивтік қабілеттілігін дамыту әдістемесі


Ж. Досмұхамедов атындағы педагогикалық колледжі
КУРСТЫҚ ЖҰМЫС
Тақырыбы:
«Салу есептері жазықтықтағы»
Орындаған:
Тексерген:
Орал, 2014ж.
Мазмұны
Кіріспе . . . 3
1. Салу есептері оқушылардың конструктивтік қабілеттілігін дамытудың құралы ретінде
1. 1 Геометрияны оқытуда есептерді шеше білу дағдысын қалыптастыру . . . 7
1. 2 Стандартты емес планиметрия есептерін шығару тәсілдері . . . 12
2. Планиметриядағы салу есептері
2. 1 Жазықтық арқылы беттердің қиылысу сызығын салу . . . 14
2. 2 Салу есептері тақырыбына арналған сабақ жоспары . . . 21
2. 3 Салу есептерін орындаудағы алгебралық өрнек . . . 27
Қорытынды . . . 29
Қолданылған әдебиеттер . . . 30
Кіріспе
Зерттеу өзектілігі. Орта мектепте математикалық білім берудің негізгі мақсаты-оқушылардың математикалық мәдениетін тәрбиелеу. Бұл тек қана оқушыларға белгілі көлемдегі математикалық білімдерді беру және нақты біліктері мен дағдыларын қалыптастыру емес, ең алдымен оқушылардың ойлау қабілетін дамыту, оларды математикалық іс-әрекеттердің әдістері мен тәсілдеріне үйрету, тұлғаның математикаға тұрақты қызығушылығын, адамгершілік және эстетикалық қасиеттерін тәрбиелеу. Оқушылардың математикалық дайындығының жоғарғы дәрежесіне жетуге мүмкіндік жасайтын құралдардың бірі-олардың математикалық есептерді шығарудағы іс-әрекеттері болып табылады. Негізгі рольді геометрия саласындағы ойлау іс-әрекетінің конструктивті компонентінің мазмұнын жете түсінуді қамтамасыз ететін есептер атқарады.
Конструктивтік есептерді шығару барысында ойлау іс-әрекеттері компоненттерінің арасындағы байланыстар байқалады: кеңістіктік, логикалық, метрикалық, интуитивтік, конструктивтік және символдық, ал олай болса, мектеп геометрия курсының сәйкес мазмұнды-әдістемелік бағыттары да бойынша оларды шығарудың әдістері мен тәсілдерін таңдаудың кең мүмкіндіктері, әртүрлі қолданыстары, сонымен қатар ішкі және пәнаралық байланыстарын кеңінен іске асыру олардың айрықша ерекшелігі болып табылады.
Геометриялық салу - кейбір геометриялық есептерді абсолют дәл деп ұйғарылатын әр түрлі аспаптардың (сызғыштың, циркульдің, тағы басқа) көмегімен шығару. Есептердің түрі аспаптардың таңдап алынуына тәуелді болады. Салу есептері циркуль мен сызғыштың көмегімен, ізделініп отырған нүктелердің координаттары операциялар (қосу, көбейту, бөлу және квадрат түбір табу) саны шекті болып келген өрнек түрінде жазылса ғана шығарылады. Егер мұндай өрнек табылмаса, онда салу есебін циркуль мен сызғыштың көмегімен шығаруға болмайды. Мысалы, мұндай есептерге кубты екі еселеу, бұрыштың трисекциясы, дөңгелек квадратурасы жатады. Циркуль мен сызғыштың көмегімен шығарылатын кез келген салу есебін бір ғана циркульмен не сызғыштың (кейде бұрыштықпен) өзімен де шығаруға болады.
Кез келген тетіктер әртүрлі шектеулі жазық және кисық беттерден (цилиндрлі, коникалық, сфералық және т. б. ) тұратын құрамды денелерден тұрады. Тетіктер түзетін геометриялық дене элеметтерді, ол беттердің қиылысуы жазықтығы деп аталатын жазықтықта бір-бірімен қиылысады.
Құрылымды көрсететін сызбада осы жазықтықтардың жобаларын құру керек. Беттік материалдардан дайындалатын тетіктердің сызбасын орындауда сызба бойынша жұмыс жасайтын жұмысшылар қиылысу беттерінің жазбасын құруы керек, қиылысу сызықтары мейілінше нақты құрулуы керек.
7-9 сыныптар геометрия курсының ажыратылмайтын бөлігі болатын конструктивтік есептер жүйесін жасау проблемасы осы уақытқа дейін шешілмеген. Бұрынғы жылдары мектеп планиметрия курсын жасағанда салу есептері оқытудың арнайы объектісі болып еді. Қазір мектеп геометрия курсында геометриялық салуларды оқыту эпизодтық сипат алып отыр.
Бұған қоса, геометрияны оқыту процесінде оқушылардың конструктивтік қабілетін дамыту мәселелері бұрын соңды жекелеген тақырып төңірегінде талқыланбаған.
Зерттеу объектісі: орта мектепте геометрияны оқыту процесі.
Зерттеу пәні : геометриядағы жазықтықтағы салу есептері
Зерттеудің мақсаты - орта мектепте геометрияны оқытуда оқушылардың конструктивтік қабілеттіліктерін дамытуды теориялық тұрғыдан негіздеп, оны жүзеге асырудың әдістемесін жасау, планиметриядағы салу есептерін шығару әдістерімен танысу.
Зерттеудің міндеттері:
- орта мектепте геометрияны оқытуда оқушылардың конструктивтік қабілеттілігін салу есептері негізінде қалыптастыруды ғылыми-әдістемелік тұрғыдан негіздеу;
- салу есептерін іріктеудің ерекшеліктері мен оларға қолданатын әдістемелік талаптарын анықтау, есептердің деңгейлерін анықтау;
- геометрияны оқыту барысында оқушылардың конструктивтік қабілеттілігін дамыту әдістемесін жасау және олардың тиімділігін тәжірибелік эксперимент барысында тексеру.
Зерттеудің болжамы : егер мектеп геометрия курсына геометрия курсын түгел қамтитын мазмұнды-әдістемелік бағыттардың бірі ретінде салу есептер жүйесін негіздеп кірістірсе, онда бұл көрнекілік-практикалық және логикалық-дедуктивті тәсілдердің өзара байланыстары негізінде оқушылардың слау қабілеттілігін дамытудың мақсатты бағытталған процесін қамтамасыз етеді, геометрия курсын меңгеруде жоғары дәрежеге жетуге жағдайлар жасайды.
Зерттеу жұмысының теориялық және әдістемелік негіздері : таным, білім, жеке тұлға және оның іс-әрекеті, ақыл-ой, құндылық туралы философиялық, психологиялық, педагогикалық теориялар мен тұжырымдамалар, білім сапасы теориялары.
Зерттеу көздері: Қазақстан Республикасы 2015 жылға дейінгі білім беруді дамыту Тұжырымдамасы, Қазақстан Республикасы жалпы білім берудің мемлекеттік жалпыға міндетті стандарттары, пәндік оқу бағдарламалары, оқу-әдістемелік кешендері; мұғалімдердің, диссертанттың педагогикалық эксперимент нәтижелері.
Зерттеу әдістері : қарастырылып отырған мәселелерге байланысты философиялық, психологиялық, педагогикалық және әдістемелік еңбектермен оқып танысу және оларға талдау жасау; математика пәні бойынша жасалған оқу бағдарламаларын, оқулықтарды талдау; математикалық білім беру жөніндегі озат педагогикалық тәжірибелермен танысу және жинақтау; оқушылардың оқу сапасының нәтижесін талдау, тәжірибелік-эксперименттік жұмыс жүргізу және қорытындылау.
Зерттеу базасы : №7 орта мектеп.
Зерттеудің ғылыми жаңалығы:
- оқушылардың салу қабілетін дамыту құралы ретінде салу геометрияның есептерін, практикалық мазмұнды есептерді пайдалану;
- осы жұмыстардың тиімділігін қамтамасыз ететін әдістеме жасау.
Зерттеудің теориялық және ғылыми маңыздылығы :
- оқушылардың математикалық қабілеттілігін дамытуда конструктивтік геометрияны оқытудың тиімділігі ғылыми негізделді;
- есептерді жүйелеу, тапсырмаға шығармашылық компонент қосу, оқушының өзіндік жұмыстарға белсенділігі, олардың жас және жекелей ерекшеліктері есепке алына отырып геометрияның жүйелі курсын оқыту барысында және факультативтік сабақтарда конструктивтік геометрияны оқыту методикасының ғылыми негіздемесі жасалды.
Зерттеудің практикалық маңыздылығы :
- салу есетерін оқыту бойынша ұсынылатын әдістеме жасалды;
- 7-9 сынып оқушыларының конструктивтік қабілеттілігін дамытуға бағытталған геометриялық салу есептерінің жүйесі құрылды;
- факультативті сабақтарға конструктивтік есептер жүйесі қарастырылды.
Зерттеу жұмысының құрылымы: кіріспеден, екі тараудан, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады.
1. Салу есептері оқушылардың конструктивтік қабілеттілігін дамытудың құралы ретінде
1. 1 Геометрияны оқытуда есептерді шеше білу
дағдысын қалыптастыру
Қазіргі ғылымдағы әдістемелік принципке сәйкесті конструктивтік процесті шығармашылық процестің аса қажетті ішкі жүйесі деп қарастыруға болады.
Конструктивтік процесстің негізгі компоненттері - есептің шартын түсіну, оның шешімінің негізгі ұғымын салу және шешімінің жалпы жоспарын тиянақтау. Іс-әрекетті жоспарлау ой-әрекетін ұйымдастыруға, шешімін іздеуге мүмкіндік береді және мұндай реттестіру әрекеті жаңа есептің шешімін сәтті аяқтауға, шығармашылық процессті соңына дейін жеткізуге көмектеседі.
Конструктивтік ойлау - басқа да ойлау түрі секілді шығармашылық есептерді шешуге бағытталған және есептің шарттары мен талаптарына сай ақпараттарды түрлендіру болып келеді, бірақ ойлаудың басқа түрлерінен ерекшелігі, сәйкесті форма не функцияның конструкциясын құру - негізгі мақсаты болып табылады.
Қазіргі таңда конструкциялаудың негізгі үш түрі қарастырылады:
- бейне бойынша немесе құрал бойынша конструкциялау;
- модель бойынша конструкциялау;
- берілген шарт бойынша конструкциялау, проектілеу;
- бұларды мұғалімнің сабақта қолдануы оқушылардың конструктивтік қабілеттілігін дамытуда ерекше роль атқарары сөзсіз.
Сонымен қатар, оқушылардың логикалық ойлау қабілетін, графикалық дағдыларын және конструктивтік қабілеттілігін дамытуда геометриялық салу есептерінің де маңызы зор.
Мектеп геометрия курсының негізгі мәселерінің бірі - геометриялық салулар. Салуға арналған геометриялық есептер оқу процесінде негізгі роль атқарады. Олар теориялық материалды жақсы түсінуге мүмкіндік береді, оқушылардың логикалық ойлау қабілетін және олардың конструктивтік қабілеттілігін дамытуға көмектеседі, графикалық дағдыларын қалыптастырады.
Салу есебі физика және сызу пәндерімен де тығыз байланысты. Физикалық шамалардың өзгерісін графиктік жолмен сипаттауға салу есептері қолданылады. Сызу сабағында оқушылар геометриялық фигураларды салудың кейбір әдістерін нақты практикалық іс-әрекеттерінде пайдаланады. Инженерлер мен техниктер кейбір практикалық жұмыстарды графиктер мен сызбалардың көмегімен орындайды. Техниканы дамытуда сызба геометрия, геометриялық салулар, сызбалардың теориясы өте зор роль атқарады [11] .
Геометриялық есептерді шешуде оқушылардың ойлауын қалыптастыру және дамыту олардың графикалық мәдениетін, суреттерді сала алуын, есепті визуальді елестету дағдылары мен мүмкіндіктерін қалыптастырады.
Геометрияны оқытуда есептерді шеше білу дағдысын қалыптастыру және оны жалпы түрде дамыту аса маңызды мәселелердің бірі болып табылады. Геометриялық есептерді шешу туралы жалпы білік-дағдылар әдетте көптеген есептерді шешу арқылы қалыптасады. Олай болса, студент пен оқытушының не мұғалім мен оқушының жүйелі түрде ұзақ уақыт еңбектенуіне тура келеді. Шешілу жолы беймәлім, әртүрлі теориялық фактілерді байланыстыруды қажет ететін, студенттер шығара алмайтын жаңа есептер де жиі кездеседі.
Сондықтан кез келген геометриялық есепті шешудің жалпы тәсілдерімен қаруландыру керек. Бұл талап математикалық есептерді шешу практикумының бағдарламасында да айтылған.
Практикум белгілі бір есептердің түрлерін және оларды шешудің тәсілдерін таныстыруға бағытталып қана қоймай, қайта дәлелдеудің барынша жалпы әдістерін ойлауды меңгерту болып табылады.
Оқытушы әрбір есепті шығартқанда, оның шешімін әдістемелік талаптарға сай іздеуге, соңында мақсатқа сай дұрыс шешімді табуға жәрдемдесетіндей талдау тәсілдері мен болашақ мұғалімдерге қажетті білім-білік дағдыларын қалыптастыруға ұмтылады. Теориялық және әдістемелік білім мен әдіс-тәсілдерінсіз кез-келген әдістемелік есепті шешуге бола бермейді. Практикадан байқалатындай, көбінесе геометрия есептері әр түрлі тәсілдермен логикалық тұрғыда көбірек ойлануды қажетсінеді. Геометрия есептерін шешудің кезеңдерін білу оқушылар мен студенттерде қалыптастырылуға тиісті аса маңызды дағдылардың бірі. Есептерді шешу процесі келесі кезеңдерден тұрады.
1) Есептің шартын түсіну:
а) есепті талдау;
б) есеп шартын схема түрінде жазу.
Есепті талдағанда оның шарты қандай, онда қандай талап қойылған (не берілген, не белгілі, есеп шарты неден тұрады?) екені анықталады. Есеп шартын схема түрінде жазғанда оның сызбасы қоса қарастырылады, осы талдаудың нәтижесінде есеп шартындағы ең керекті, таныс элементтер ескеріліп, олар қысқаша жазылады. Есепті талдау мен оның сызбасын және шартын схема түрінде қысқаша жазу - есепті шешу үшін жоспар іздеудің негізгі құралы болып табылады. Есепті талдай келе осы есепке қандай мөлшерде теориялық білімнің қажет болатындығы анықталады.
2) Есеп шешімін іздеу - есепті шешудің тәсілін іздеу, бұл бүкіл процестің негізгі бөлігі болып табылады. Бұл кезеңде ең алдымен берілген есептің түрі (типі), яғни оның дәлелдеуге, есептеуге не геометриялық түрлендіруге берілгені анықталады, осыған орай есепті шешу тәсілі ізделеді. Есеп шартында берілген элементтер мен іздеуге, анықталуға тиісті белгісіздер арасындағы байланыс ізделеді. Есеп шешімін іздеуде бір-бірімен тығыз байланысты мынадай екі жақты мәселені анықтайды:
а) белгілі теориялық білімді шешілуге тиісті есеп шартына сай түрлендіру;
б) есеп шартын белгілі теориялық фактілерге сәйкес және оларға байланысты түрлендіру. Бұл арада теориялық білім деп отырғанымыз математикалық ұғымдар мен олардың анықтамалары, теоремалар және математикадағы негізгі әдістер (координаттар әдісі, векторлық әдіс, геометриялық түрлендірулер мен теңдеулер құру әдісі және т. б. ) . Есептердің түрі мен құрылысына қарай оларды кластарға жіктеп талдау мен шешу әдістерін таңдап алады. Әсіресе, бірнеше теориялық материалдарды біріктіретін, әрі күрделі, әрі көптеген есептерді шешуге теориялық әдістемелік негіз болатын тірек есептерін талдау кезінде белгілі бір гипотеза ұсынылады және оның іске асырылуы тексеріледі. Есеп шешімін іздеу үшін гипотеза ұсына отырып, осы есепке нақтылы қандай теориялық материал керек болатынын анықтаймыз. Теориялық білімді негіздеуші әдісті таңдап, гипотезаны тексереміз. Егер есепті талдағанда бұрыннан таныс элементті байқасақ, не ол шешілуі таныс есепке ұқсас болса, онда есепті шешу үшін белгілі әдісті қолдану мүмкіндігі туралы ой, не есепті шешу жоспары пайда болады. Егер есептің таныс емес түрін шығаруға тура келсе, онда одан бұрыннан таныс есептердің кемінде бір элементін іздейміз немесе берілген есеп шартын бұрын шешілген есептегі таныс бір элемент табылатынын талдаймыз.
3) Жоспарды іске асыру. Бұл арада шешу идеясы табылып, есеп шешіледі.
4) Шешілген есепті талқылау:
а) есеп шешімін тексеру;
б) есепті зерттеу;
в) есеп шешімін әр түрлі параметрлер мен байланыстар бойынша талдау.
Есептің шешілуінің және оған қолданылған әдістер мен теориялық негіздеулердің дұрыс екенін, ол шешім есеп шартының барлық талаптарын қанағаттандыратынын білу үшін оны тексеру керек. Есепті зерттеу келесі мәселелерді анықтауы керек: қандай шарт орындалғанда есептің шешімі бар; қандай шарт орындалғанда есептің жалпы шешімі жоқ болады?
Есептің шешімін талдау мынадай мәселелерге жауап береді. Есепті шешудің бұдан басқа ең тиімді жолы жоқ па? Есепті жалпылауға бола ма? Осы есептен қандай қорытындылар жасауға болады? Есепті шешу процесінің құрылымы ең алдымен есептің сипатына, есеп шығарушының қандай біліммен, білікпен, дағдымен қаруланғанына тікелей байланысты.
Лобачевский Геометриясы - евклидтік емес геометрияның бір түрі; Евклид геометриясындағы параллель түзулер жөніндегі аксиома қарама-қарсы мағыналы аксиомоға ауыстырылған. Евклид “Негіздерінде” параллель түзулер жөніндегі аксиома былайша тұжырымдалған: берілген түзудің бойында жатпайтын нүкте арқылы осы түзумен бір жазықтықта жататын және онымен қиылыспайтын бір ғана түзу жүргізуге болады. Ал Лобачевский геометриясы оның орнына мынадай аксиома қолданылады: берілген түзудің бойында жатпайтын нүкте арқылы осы түзумен бір жазықтықта жататын және онымен қиылыспайтын кем дегенде екі түзу жүргізуге болады. Лобачевский геометриясын Н. И. Лобачевский жасап дамытқан. Сәл кейін осындай теорияны Я. Больяй (1802 - 1860) да дәлелдеген. Сондықтан, Лобачевский геометриясы кейде Лобачевский - Больяй геометриясы деп те аталады. Евклидтен Лобачевскийге дейінгі 2 мың жылдан аса уақыт аралығында көптеген ғалымдар К. Птолемей, Д. Прокл, Ибн әл-Хайсам, О. Хайям, П. Катальди, Дж. Валлис, Дж. Саккери, А. Лежандр, Ф. Швейкарт, Ф. Тауринус, т. б. осы теорияны дәлелдемек болып еңбек еткен. Лобачевский геометриясын арнайы гиперболалық евклидтік емес геометрия деп атайды. Олай атау Риманның эллипс[эллипстік] геометриясына қарсы қою үшін қажет болды (қ. Риман геометриясы) .
Лобачевский жазықтығы - параллель түзулер туралы аксиомадан басқа Евклид геометриясы аксиомаларының барлығына бағынатын түзу сызықтар мен фигуралардың қозғалысы (сонымен қатар қашықтықтар, бұрыштар, т. б. ) анықталған жазықтық (нүктелер жиыны) . Осыған ұқсас жолмен Лобачевский кеңістігі де анықталады.
1. 2 Стандартты емес планиметрия есептерін шығару тәсілдері
Есеп шығару - ерекше ой жұмысы. Кез келген шарттардан және талаптардан тұратыны белгілі. Есеп шығару дегеніміз - математиканың жалпы заңдылықтарын (анықтамалар, аксиомалар, теоремалар, заңдар, формулалар) есеп шартына немесе оның салдарына белгілі бір ретпен қолдана отырып, есеп талабына жауап беру болып табылады. Сонымен есеп шығару, оның шартына белгілі бір математикалық ережелерді сәйкес түрде қолдана отырып, талабына қарай жылжитын ой қозғалысы.
Теорияға байланысты стандартты және стандартты емес есеп түрлері белгілі. Дайын ережелердің көмегімен шығарылатын есептер стандартты делінеді де, ал шығару жолдары дайын ережелер арқылы табыла қоймайтын есеп - стандарттық емес болып табылады.
Қандай да болмасын есепті шығаруды негізгі төрт кезеңге бөлуге болады:
1. Есептің шарты мен талабын терең түсіну. Есепті дұрыс түсініп алмай, оны әрі қарай жалғастыру мүмкін емес. Есеп шығаруға кіріспес бұрын оның мазмұнына талдау жасап, не берілгенін, нені табу керек екендігін анықтап алған қажет. Бұл тұста ұқыпты сызылған сызбалардың немесе сүлбелердің маңызы зор. Есептің берілген не ізделінді элементтері белгіленбеген болса, онда ыңғайлы белгілеулер енгізу керек.
2. Есепті шығарудың жоспарын құру. Бұл - шешуші кезең. Шығару жоспары дұрыс құрылғанда ғана есеп қатесіз шығарылады. Жоспар құру үшін есеп шығарудың негізгі «кілтін» ұсынатын идеяларға байланысты сұрақтар мен ақыл-кеңестер жүйелі түрде құрылғаны орынды:
- осы сияқты бұрын кездескен есептерді қарастыру. Екі есептің берілген жағдайын салыстыру;
- шығарылатын есепке ұқсастау есептің жоспарын басшылыққа алу;
- есепке жақындайтын бұрыннан белгілі есеп табылмаған жағдайда есеп шартындағы ұғымдардың анықтамасын пайдалану, қасиеттерін еске алу; есеп шарты мен талабын математикалық тілге көшіру,
- есеп жоспарын құру кезінде берілгендерінің барлығын қолдану,
- есеп шарты немесе талабын түрлендіру,
Жоспар бойынша
3. Жоспарды жүзеге асыру;
4. Есепті тиянақтау. Жоспар жүзеге асырылған соң, онымен тынып қалмай есеп шығару порцесін тағы да ой елегінен өткізу керек. Міндетті түрде нәтиже мен шығару жолы тексеріледі. Онымен қоса «Есепті шығарудың басқаша жолы бар ма?», «нәтижені басқаша қалай алуға болады?» т. б. сұрақтарға жауап іздеп, тиянақтаған дұрыс.
2. Планиметриядағы салу есептері
2. 1 Жазықтық арқылы беттердің қиылысу
сызығын салу
Бір жазықтықтың екі - жазықтықпен қиылысу сызығын салудың жалпы әдісі болып кейбір қима жазықтықтар және қосымша қима сфералар арқылы бұл сызықтың нүктелерін табады.
Цилиндрлік, коникалық, сфералық қосымша жазықтықтар арқылы қиылысқан сызығын анықтау және қосымша қима сфералардың қиылысу сызығын табу мысалы төменде көрсетілетін болады.
Екі өзара қиылысқан беттердің сызығын табу үшін, екі бетті де қиып өтетін қосымша қима жазықтықтарды немесе қима сфераларды қолданады. Қосымша қима беттердің берілген беттерді қиып өтетін қима сызығының нүктелері, екі берілген қима беттердің қиылысу сызығын береді.
Келістіруші деп аталатын қосымша қима жазықтықтарды немесе сфераларды таңдау барысында бұл келістірушілер шеңбер сызығы немесе түзу сызығы бойымен берілген екі бетті де қиып өтетіндей етіп ұмтылады.
Екі беттің қиылысу сызығын салу барысында қосымша қима бетті берілген бетпен қиылысқан жағдайда жай сызықтар болып шығатындай етіп таңдайды (мысалы, түзулер немесе шеңберлер) .
Қосымша қима беттердің орнына жазықтықтар немесе сфералар алынады. Сызықты салу есебін шығару барысында қосымша қима жазықтық ретінде деңгейлік жазықтықтар ретінде - проекция жазықтығына параллель жазықтықты алады.
Екі беттің сызығы (бас тірек) нүктелерін, олармен қима сызығын салуын бастаймыз. Олар қандай шектерде нүктелерді анықтауға қосымша қима жазықтықтарды көруге болатынын анықтайды.
Өзінің түзу болатын осі арқылы қима беттің сызығын анықтау әдісі. Бұл әдіс қиылысу сызығын салуға қолданылады:
а) екі коникалық бет;
б) коникалық және цилиндрлік бет;
в) пирамида немесе призма беттің коникалық бет;
г) екі цилиндрлік бет;
д) цилиндрлік бет пирамида немесе призма бетпен.
Эллиптикалық цилиндрдің жартысферамен қиылысуы
Берілген мысалда қосымша деңгейлік жазықтықтар П1 және П2 жазықтықтарға параллель болуы мүмкін.
1 - жағдайда фронталь жазықтықтар сфераны шеңбер бойынша, ал цилиндрді түзусызықты жасаушы арқылы қияды.
Солардың 1 жазықтығы альфа беттермен а шеңбер доғасымен және түзу сызық в-мен қиылысады. Бір нүктесі а шеңбер доғасы мен в түзу сызығы ізделінді қисыққа жатады.
Қосымша қима В жазықтығы (бас фронталь жартысфера меридиан жазықтығы) арқылы бас жартысфера меридиан мен шеңбер доғасы мен сызықтар мен қиылысу нүктелері сияқты 2 және 3 нүктелері табылған з жазықтығы - бас фронталь меридианның цилиндрі, ол жартысфераны к - шеңбер доғасы бойымен қияды, ал
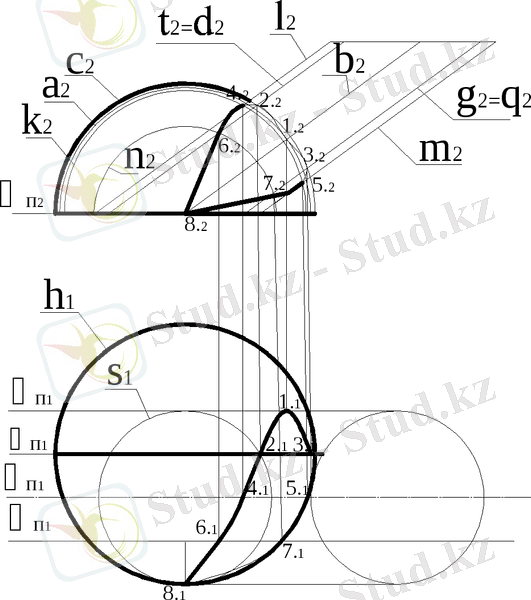
1 сурет - Сфера мен эллиптикалық цилиндрмен қиылысуы
бұл өзінің қатарында цилиндрдің фронталь меридианмен 1 және т қиылысып, 4 және 5 нүктенің орнын анықтайды.
8 нүктесі горизонталь проекция жазықтығына параллель және жартысфераны шеңбер бойымен - һ экваторы, ал цилиндр S табанының шеңбермен қиятын w фронталь проекциялаушы жазықтық арқылы табылады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz