Стереометриядағы салу есептерін шешу теориясы мен әдістемесі


Ж. Досмұхамедов атындағы педагогикалық колледжі
КУРСТЫҚ ЖҰМЫС
Тақырыбы:
«Стереометрияда салу есептері»
Орындаған:
Тексерген:
Орал, 2014ж.
Мазмұны
Кіріспе . . . 3
1. Стереометриядағы геометриялық салулар теориясы
1. 1 Стереометриядағы салу есептерін шешу әдістері . . . 7
1. 2 Стереометриялық фигураларды кескіндеу . . . 11
2. Стереометриядағы салу есептері
2. 1 Кескіннің метрикалық анықталғандығы туралы түсінік . . . 13
2. 2 Кеңістік фигурасының кескіні . . . 15
2. 3 Салу есептері тақырыбына арналған сабақ жоспары . . . 17
Қорытынды . . . 29
Қолданылған әдебиеттер . . . 31
Кіріспе
Мектеп геометрия курсын оқытудың өзіндік қиындыктары бар. Әсіресе, стереометрияның алғашқы сабақтарынан бастап кездесетін қиындықтар жоғарғы сыныптарда сабақ беретін әрбір математика мұғаліміне таныс. Стереометрия аксиомаларымен таныстыру кезінде оқушылардың кеңістіктік тусініктерінің әліде нашар дамыған болуына байланысты, стереометрияның алғашқы ұғымдары туралы мәліметтер абстрактілі сипатқа ие болып, жаттанды білімдер қалыптасады. Сондыктан да, оқушылардың көпшілігі стереометрия курсын мектеп пәндерінің ішіндегі күрделі пәндердің бірі ретінде қабылдап, оған деген қызығушылықтары жойылады. Сол себепті геометрияны оқытуда оқытылып жатқан материалдын көрнекілігі және оның моделдеу немесе басқа бейнелеу кұралдарын пайдалану арқылы нақтылануы осындай қиындыктарды жеңуде үлкен роль атқарады.
Көп жағдайда геометрия сабағында мұғалім баяндап жатқан оқу материалын сынып тақтасында кескіндеу арқылы толықтырып отырады. Осы жағдайда мұғалім геометриялық фигуралардың кескіндерінің көбінесе көрнекі орындалуына ғана көңіл бөледі. Бірақ теорияға суйенбей орындалған мұндай сызбалар практикада көптеген қателіктерге алып келеді. Көп жағдайда мұғалімнің өзі де қатесін байқамайды, тіпті қате болады деп күдіктенбеуі де мүмкін. Ал бұл сызбаны оқушы өз дәптеріне де, осы түрде көшіріп алатындығы түсінікті. Мұндай дүрыс емес сызбаларды қолдану оқушылардың білімдерінің, кеңістіктік түсініктерінін т. с. с. дұрыс қалыптасуына кері әсер етеді.
Геометрияны оқытудағы кескіндерді пайдалану барысында кездесетін осындай қиындықтарды шешу және жіберілетін қателіктерді болдырмау проблемасын кез - келген математика мұғалімі білуі керек деп ойлаймыз. Сондықтан бұл жұмыста осы мәселеге тоқталып отырмыз.
Геометрияны оқытуда фигураларды кескіндеу және осы кескіндерді сабақта пайдалану үлкен әдістемелік мәнге ие болумен қатар, мынадай екі жақты сипатқа ие. Бір жағынан, геометриялық фигуралар мен олардың заңдылықтарын кескіндеу геометрияны оқытуды көрнекі етіп, оны меңгеруді женілдетеді. Бұл жағдайда, геометриялық кескіндер иллюстративтік - рөл атқарады да, сондықтан оларды иллюстративті сызбалар деп атауға болады. Екінші жағынан, фигуранын кескіні қандай да бір геометриялық есепті шешу құралы болып табылуы мүмкін. Мұндай түрдегі кескіндер есепті шешуші сызбалар болып табылады.
Екі жағдайда да геометриялық фигураны кескіндеу үшін проекциялау әдісі қолданылады және алынған сызбалар "проекциялық сызба" деп аталады. Бірақ проекциялық сызбалардың берілуі мен қолданылуындағы ерекшеліктері оларға қойылатын талаптарға үлкен өзгерістер енгізеді. Иллюстративті сызбалар үшін негізінен оның көрнекілігі мен оңай орындалуына көңіл бөлінсе, ал есепті шығару үшін пайдаланылатын сызбаларда, есепті шығаруға мүмкіндік беретін оның толықтығы мен кескіннің дұрыс болуы негізгі рөл атқарады.
Зерттеу жұмысының өзектілігі: Мектеп геометрия курсындағы, оқушылардың кеңістіктік түсініктерін қалыптастырудың қажетті құралдарының бірі сызбалар, яғни есепте қарастырылып жатқан кеңістік фигураларының параллель, проекциядағы кескінін салу болып табылады. Зерттеушілердің пікірінше сызба "моделдер мен абстрактті кеңістіктік түсініктің арасын байланыстырады". Сызбаны сабақта қолданудың да өзіндік қиындыктары бар. Себебі екі-өлшемді объектіні кескіндеуге қарағанда, үш өлшемді объектіні кескіндеу принципі басқаша. Егер жазық фигураның кескіні, есеп шартында берілген фигураның қасиеттерін түгел сақтай отырып ұқсастық дәлдігіне дейін бейнелейтін болса, ал кеңістік фигурасының кескінінде түпнұсқаның, яғни есептегі қарастырылып отырған, үш өлшемді фигураның элементтері арасындағы кеністіктік және сандық қатынастары өзгеріске ұшырайды. Жазық фигураны кескіндегенде ешкандай геометриялық проблема тумайды. Сызба түпнұсқаның дәл көшірмесі болады немесе оған ұқсас фигураны береді. Мысалы, сызбадағы дөңгелектің кескінін қарастыра отырып, дөңгелектің өзін көріп отырғандай боламыз.
Кеңістік фигураларын кескіндеу, тіпті басқаша. Өкінішке орай, ұшы ауада із қалдыратындай "кеңістік каламы" болмайды. Мұндай қаламмен қырларын жүргізе отырып кәдімгі кубты салуға болар еді. Ал мұндай қалам болмағандықтан кәдімгі қаламмен кубты қағаз бетіне кескіндеуге тура келеді. Жазық кескін кеңістік фигурасының дәл өзі болуы мүмкін емес. Сол себепті, кеңістік фигурасын қандай ережемен кескіндегенде түпнұсқаны мүмкіндігінше дұрысырақ бейнелейді деген проблема туындайды. Мұндай талаптар екеу; көрнекілік және оңай өлшенімдік.
Зерттеу жұмысының жаңалығы: Кеңістіктегі фигураларды кескіндеудің әр түрлі әдістерін анықтау.
Зерттеу жұмыстың практикалық құндылығы: геометрияны оқытуда фигураларды кескіндеу және осы кескіндерді сабақта пайдалану үлкен әдістемелік мәнге ие болумен қатар, мынадай екі жақты сипатқа ие. Бір жағынан, геометриялық фигуралар мен олардың заңдылықтарын кескіндеу геометрияны оқытуды көрнекі етіп, оны меңгеруді женілдетеді. Бұл жағдайда, геометриялық кескіндер иллюстративтік - рөл атқарады да, сондықтан оларды иллюстративті сызбалар деп атауға болады. Екінші жағынан, фигуранын кескіні қандай да бір геометриялық есепті шешу құралы болып табылуы мүмкін. Мұндай түрдегі кескіндер есепті шешуші сызбалар болып табылатындығында.
Курстық жұмыстың мақсаты - мектеп геометрия курсындағы стереометрия тақырыптарын терең меңгеру, толық қарастыру, бір жүйеге келтіру, математика сабағының танымдық деңгейін көтеру, оқушылардың математика пәніне деген қызығушылығын арттыру, дамыту.
Курстық жұмыстың міндеттері :
- Кеңістік фигураларының және олардың жалпы қасиеттерін оқып-үйрену және жүйелеу;
- Кескіндеудің теориялық негізін оқып-үйрену;
- Нақты кеңістік қасиеттері мен ондағы геометриялық фигуралардың және олардың элементтері арасындағы сандық, сапалық қатынастары туралы білімдерді менгеру
- Кеңістіктік түсініктердің теория-логикалық және образды ойлауын дамыту.
Зерттеудің ғылыми нысаны: егер жазықтықтық фигураларды кескіндеудің негізгі қасиеттерін оқыту тиімді әдіс-тәсілдермен жүргізілсе, онда болашақ математика мұғалімдері кеңістіктік фигуралардың жазықтыққа кескіндеудің тәсілдерін жақсы меңгереді.
Зерттеу объектісі: орта мектеп оқушылары
Зерттеу базасы: №1 орта жалпы білім беретін мектебі
Зерттеу жұмыстың әдіснамалық негіздері: жоғары алгебра, математика пәндерін оқытудың теориясы мен әдістемесі, философиялық және психологиялық - педагогикалық тұжырымдамалар. Жеке тұлғаның математикамен айналысудан қалыптасатын интелектуалды қасиеттерін тәрбиелеу.
Міне осындай шоғырланған проблемаларды шешуге арналған түрлі әдебиеттерге талдаулар жасай отырып, бұл жұмыста осы мәселелерді бір жүйеге келтіруді және мектеп математика пәнінің мұғалімдерінің қолдануына болатындай әдістемелік мәселелерді қамтуды мақсат еттім.
Құрылымы: кіріспеден, екі бөлімнен және қорытынды мен пайдаланылған әдебиеттер тізімінен тұрады.
1. Стереометриядағы геометриялық салулар теориясы
1. 1 Стереометриядағы салу есептерін шешу әдістері
Салу есептері циркуль мен сызғыштың көмегімен, ізделініп отырған нүктелердің координаттары операциялар (қосу, көбейту, бөлу және квадрат түбір табу) саны шекті болып келген өрнек түрінде жазылса ғана шығарылады. Егер мұндай өрнек табылмаса, онда салу есебін циркуль мен сызғыштың көмегімен шығаруға болмайды. Мысалы, мұндай есептерге кубты екі еселеу, бұрыштың трисекциясы, дөңгелек квадратурасы жатады. Циркуль мен сызғыштың көмегімен шығарылатын кез келген салу есебін бір ғана циркульмен не сызғыштың (кейде бұрыштықпен) өзімен де шығаруға болады.
Мектеп оқушыларының кеңістікті қабылдап, оны көз алдына елестете алуы стереометрияны оқытудың негізгі мәселелерінің бірі болып саналады. Осы айтылған мақсатты іс жүзіне асыруда кеңістіктегі салуға берілген есептерді шешудің зор мәні бар. Жазықтықтағы геометриялық салулар теориясы жеткілікті түрде талқыланып қарастырылады, ал стереометрияның әдістемелік мәселелеріне әлі де толық көңіл бөлінбей келеді. Геометриялық салулар теориясы - салуды негіздеу, есептерді кластарға жіктеу, есеп шешу әдістері, белгілі бір класқа жататын есептерді шешу критериі, салу есептерін шешкенде барынша жай әдістерді тиімді қолдану сияқты мәселелерді қарастырады.
Кеңістіктегі салу есептерін кластарға жіктеу туралы әр түрлі көзқарастар мен тәсілдер бар. А. Н. Чалов кеңістіктегі салу есептерін геометриялық салуды орындау тәсілдері бойынша келесі топтарға бөледі:
1) елестету арқылы шешілетін есептер;
2) проекциялық сызбамен шешілетін есептер;
3) модельмен шешілетін есептер.
Салуға берілген стереометрия есептерін позициялық және метрикалық деп екі топқа бөлетіндер де бар. Негізгі элементтерінің қиылысуын ғана іздейтін, соны салумен аяқталатын есептер позициялық әдіспен шешілетін есептерге жатады. Кесінді салу, белгілі бір шамасы бар бұрышты салу, перпендикуляр тұрғызу, биссектриса жүргізу және т. б. белгілі шарттарды қанағаттандыратын фигура салу талабы қойылатын есептер метиркалық есептерге жатады. Мысалы, В. А. Гусев, В. Н. Литвиненко, А. Г. Мордкович өздерінің құрастырған «Математикалық есептер шешу практикумында» кеңістіктегі салуға берілген есептерді мынадай әдістер бойынша топтарға бөледі:
1) кеңістіктегі қарапайым салулар;
2) нүктелердің геометриялық орындары;
3) кейбір нүктелердің геометриялық орындары мен түзулерді пайдалану;
4) кескіндеу арқылы салу.
Салуға берілген стереометрия есептері талдау, салу, дәлелдеужәне зерттеу сияқты төрт кезеңнен тұрады.
Талдау - бір бүтінді, құрамды бөліктерге жіктейтін, әр бөлікті жеке қарастыратын зерттеу әдісі. Ол салу есебін шешудің жоспарын табуға мүмкіндік тудырады. Талдау - есеп шешудің барынша маңызды кезеңі. Есепке дұрыс жүргізілген талдау - есепті шешу жоспарын дұрыс құрастырудың кепілі. Салу есебіне талдау жасағанда сызба басты рөл атқарады. Сонда есеп шартын, сызбадағы элементтердің өзара орналасуына барынша басынан аяғына дейін талдау жасалады, есеп шартында берілгендер мен іздеген элементтер арасында байланыс орнатылады. Есептің салу кезеңінде салу есебіне қолданылатын аксиомаларды, теоремаларды, қосымша қарапайым салуларды дәл көрсету керек. Дәлелдеу кезеңі есеп шешімінің дұрыстығына күдік туғанда қажет болады. Салу есебін зерттеу кезеңінің өзіндік маңызды ерекшелігі бар. Ол қандай шарттар орындалғанда есептің шешуі бар болады және неше шешімі бар деген сұрақтарға жауап береді. Сонымен бірге зерттеу кезеңі кеңістік елесті дамытуға мүмкіндік туғызады. Салуға берілген алғашқы есепті шығарғанның өзінде есепті шешудің кезеңдерін (талдау, салу, дәлелдеу, зерттеу) дәл анықтап бөлу керек.
Кеңістіктегі салуға берілген есептерді шешудің негізгі әдістері: аксиоматикалық әдіс, проективтік әдіс, геометриялық орындар әдісі. Аксиоматикалық әдістің негізгі мәні есепті шешу кезінде салудың өзі орындалмайды, салуға берілген есеп элементар салуларға келтіріледі, кейін бұлардың бәрін бірге қарастыруға болатындай түрдегі барлық жай амалдар қарастырылады. Салу есебінде көрсетілген амалдар кейде аксиомалар деп, ал есепті шешу әдісі аксиоматикалық әдіс деп аталады. Себебі есепке қолданылатын барлық амалдар елестеу арқылы формальді түрде жүргізіледі де логикалық түрде негізделеді, мұндай әдіс формальді-логикалық әдіс деп те аталады. Әдетте логикалық ой тұжырымдары сызба арқылы жүрізіледі. Бұл есеп шешімін барынша жеңілдетеді: ойды іске қосады, көптеген геометриялық элементтер мен олардың жиынын есте сақтап қалуға, кеңістік жөнінде дұрыс түсінік орнығып қалыптасуына мүмкіндік берді. Аксиоматикалық әдіс оқушылар санасында кеңістік туралы түсініктің, логикалық ойлаудың дамуына барынша терең және берік теориялық білім алуға, әсіресе белгілі бір салуларға түсінік беретін стереометрияның алғашқы теоремаларын үйренуге мүмкіндік туғызады. Есептер шешу кезінде алдымен көрнекі құралдар -жазықтықтар моделі (нұсқасы), нүктелер мен түзулерді мақсатты түрде қолдану пайдасы зор. Осындай әдістер көмегімен салудың талаптары айқын түрде көрсетіледі, бұдан соң логикалық түрде негіздеу және логикалық негізде салынған кескінді салу дәлелденеді. Модельдеу есеп шешімін көрнекі түрде талдау жасауға, талдауды ықшамдауға мүмкіндік береді.
Проективтік әдіс (проекциялық сызбада салу есебін шешу әдісі) . Егер ерекше проекциялау ережесі бойынша геометриялық денелердің кескінін пайдалануға мүмкіндік болса, онда ол есепті сызбалық құралдың көмегімен барлық салу жұмысын орындауға болады. Мұндай кескін геометриялық денені бір жазықтыққа проекциялау жолы мен алынады және проекциялық сызба деп аталады, ал есепті шешу әдісін «проекциялық сызбада салынатын есеп» деп атайды.
Кеңістіктегі салу есептерін шешуге барынша ынғайлы әдіс -еркімізше алынатын параллель проекциялау. Ол сызбаның көрнекілігімен, оны салудың өте жай қарапайым болатынымен сипатталады. Проекциялық сызба арқылы шешілетін салу есептері төрт кезеңнен тұрады. Бірақ барлық кезеңдерді әр есепте түгел іске асыру талабы қойылмайды.
Геометриялық орындар әдісі. Кеңістікте элементтердің геометриялық орындарын табуға берілген кез келген есепті салу есебі ретінде тұжырымдауға болады. Кеңістіктегі геометриялық орындар әдісімен салуға берілген есептерді шешудің мәні төмендегі мәселелер арқылы сипатталады. Әуелі есептегі берілген шарттардың біреуінен басқасын ескерусіз қалдыра тұрамыз. Өзіміз әдейі таңдап алып қалаған бір ғана шартты қанағаттандыратын нүктелер жиынын қарастырамыз. Бұдан әрі есептің екінші шартын қанағаттандыратын нүктелер жиыны қарастырылады және т. с. с. Біз қарастырған барлық жиындардың қиылысуы есептің шешімі болады. Кеңістіктегі салу есептерін шешудің тек төрт әдісін қарастырдық. Кеңістікте салуға берілген есептерді шешудің басқа да әдістері бар. Есептер шешудің бір немесе басқа әдісін таңдап алу шешілуге тиісті есептің сипатына, есеп шығарушының дайындық дәрежесіне, т. б. байланысты. Күрделі есептерді шешу кезінде көбінесе бір мезгілде бірнеше әдіс қатарынан қолданылады.
1. 2 Стереометриялық фигураларды кескіндеу
Кескінді салудың жалпы әдістерін жеңілдету үшін, оның базистік нүктелері тиімді таңдалып алынып кейбір жеке элементтерін кескіндеу ыңғайлы бір ретпен орындалуы қажет.
Түпнұсқадан базистік нүктелер ретінде бір жазықтықта жатпайтын кез келген төрт нүктені алуғңа болады. Бірақ базистік нүктелер ретінде көпжактың төбелерін алу көпжақ кескінін салуда тиімді схемасын алуға мүмкіндік береді.
Ол төбелердін үшеуі бір табаннан ал төртінші нүкте ретінде оның төбесі алынады.
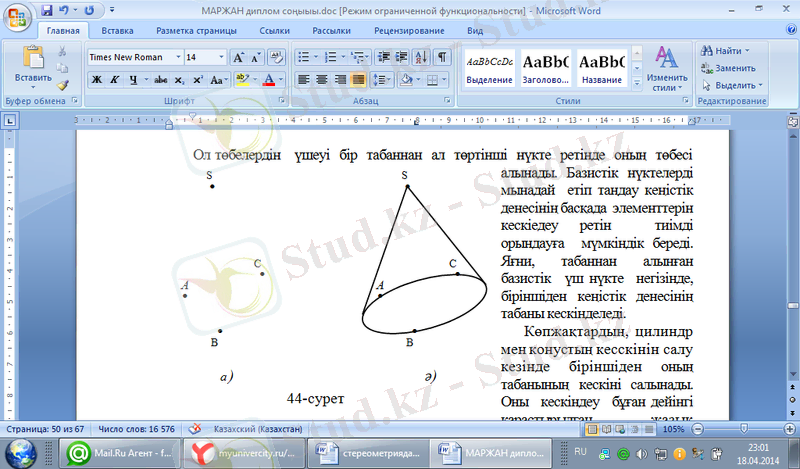
1-сурет
Базистік нүктелерді
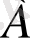 мынадай етіп таңдау кеңістік денесінің басқада элементтерін кескіедеу ретін тиімді орындауға мүмкіндік береді. Яғни, табаннан алынған базистік үш нүкте негізінде, біріншіден кеңістік денесінің табаны кескінделеді.
мынадай етіп таңдау кеңістік денесінің басқада элементтерін кескіедеу ретін тиімді орындауға мүмкіндік береді. Яғни, табаннан алынған базистік үш нүкте негізінде, біріншіден кеңістік денесінің табаны кескінделеді.
Көпжақтардың, цилиндр мен конустың кесскінін салу кезінде біріншіден оның табанының кескіні салынады. Оны кескіндеу бұған дейінгі қарастырылған жазық фигуралардың кескін салу теориясының негізінде орындалады. Яғни, көпжақ табаны дұрыс үшбұрыш, тен бүйірлі үшбұрвш бұрышты үшбұрыш болғанда оның табанын «бар болудың бірінші теоремасы» негізінде кез-келген үшбұрыш етіп саламыз. Ал табаны паралелограмм, тікбұрыш, ромб, квадрат болған жағдайда оның табанының кескінін базистік үш нүкте негізінде еркін түрде параллелограмм етіп саламыз.
Ал көпжақ табаны трапеция болғанда оның кескінін трапеция етіп саламыз. Конус пен цилиндрді кескінндегенде оның табаның бірден эллипс етіп саламыз.
Фигураның кескін салуға қойылатын талаптардың орындалуын қамтамасыз ету мақсатында төртінші базистік нуктені бірден кескіндемей, табанынын кескіні салынғаннан сон кескіндеген тиімді болады.
Мысалы, конустың кескінін салу үшін бірден төрт базистік нүктесін белгілеп алып, оның кескінін салайық. Алынған кескіннің, фигура кескініне қойылатын талаптарға (кескіннің дұрыстығы, кескіннің көрнекілігі, кескіннің оңай орындалатын болуы) сай болуына талдау жасайық. Ол үшін базистік нүкте ретінде конус табанынан үш және төбесінен бір нүкте аламыз (1, а-сурет) . Осы базистік нүктелердің табанында жатқан А, В, С нүктелерін бастыра эллипс- жүргіземіз. S төбесінен осы эллипске жанамалар жүргіземіз (1, ә-сурет) . Алынған сызба конустың дұрыс, бірақ көрнекі емес кескінін береді [9] .
Олай болса, кеңістік денелерін кескіндеуде базистік нүктелерді еркін түрде алу дұрыс, бірақ көрнекі емес кескін алуға алып келуі мүмкін екен. Осы талаптарды мүмкіндігінше сақтау мақсатында кейбір кеністік денелерінің кескіндерін салуға жеке тоқталамыз. [6]
2. Стереометриядағы салу есептері
2. 1 Кескіннің метрикалық анықталғандығы туралы түсінік.
F' фигурасының F
 α кескіні егер оған декарттық репердің кескінін жалғастыруда F' фигурасын анықтайтын барлық нүктелер, түзулер мен жазықтықтар α жазықтығында берілетіндей болса, онда ол
метрикалық анықталған
деп аталады. Олай болса, кез келген метрикалық анықталған кескін толық кескін болып табылады: кескіннің толықтығы оның метрикалық анықталғандығының қажетті (бірақ жеткілікті емес!) шарты болып табылады. Егер де F' фигурасының F кескіні метрикалық анықталған болса, онда біздер, осы кескінді пайдалана отырып, F' түпнұсқаға қатысы бар кез келген метрикалық есептерді шеше алатындығымыз шығады.
α кескіні егер оған декарттық репердің кескінін жалғастыруда F' фигурасын анықтайтын барлық нүктелер, түзулер мен жазықтықтар α жазықтығында берілетіндей болса, онда ол
метрикалық анықталған
деп аталады. Олай болса, кез келген метрикалық анықталған кескін толық кескін болып табылады: кескіннің толықтығы оның метрикалық анықталғандығының қажетті (бірақ жеткілікті емес!) шарты болып табылады. Егер де F' фигурасының F кескіні метрикалық анықталған болса, онда біздер, осы кескінді пайдалана отырып, F' түпнұсқаға қатысы бар кез келген метрикалық есептерді шеше алатындығымыз шығады.
Метрикалық анықталған F кескіні F' түпнұсқаны қозғалысқа дейінгі дәлдікпен анықтайды.
Кескін метрикалық анықталған болуы үшін мәндері берілуге тиісті тәуелсіз параметрлердің р саны кескіннің параметрлік саны деп аталады.
Мектеп геометрия курсында фигура кескінінің метрикалық анықталғандығы ұғымы жиі колданылады. Метрикалық анықталған фигура кескінінен фигураның түпнұсқасын ұксастық дәлдігіне дейін қайта құруға мүмкін болады. Мысалы, берілген кескіннің кұрамында квадраттың кескіні бар болса, онда бұл кескін метрикалық анықталған болып табылады. Яғни түпнұсканы аңықтау үшін жұргізілетін кері салулар квадраттың кескіні негізінде метрикалық анықталады. [9]
Сонда, кескін метрикалық анықталмай тұрып тек параллель проекциялаудың немесе кескіндеудің 1°-4° қасиеттерінің негізінде салынады. Ал, кескін метрикалық анықталғаннан соң түпнұсканың бірде-бір нүктесін еркін түрде кескіндеуге болмайды, ол берілген метрикамен ғана анықталады.
Нақты мысалдармен көрсетпес бұрын, есеп шартын талдау мәселесіне тоқталайық. Есеп шартына талдау жасау барысында оқушылар түпнұсқа құрамына енетін геометриялық фигураларды және кескін құрамына енетін геометриялық фигураларды нақты ажыратып қарап, кескіні метриканы пітын фигураға назар аударуы кажет, Мысалы, мына ссептін шартына талдау жасайық.
«Сызба жазықтығында шеңберлдің кескіні эллипс болып берілген және осы жазықтықта нүкте мен түзу берілген. Олар сызбада сәйкесінше Р және МN әріптерімен белгіленген нүктеден түзуге түсірілген перпендикулярдың кескінін салу керек» (2-сурет) .
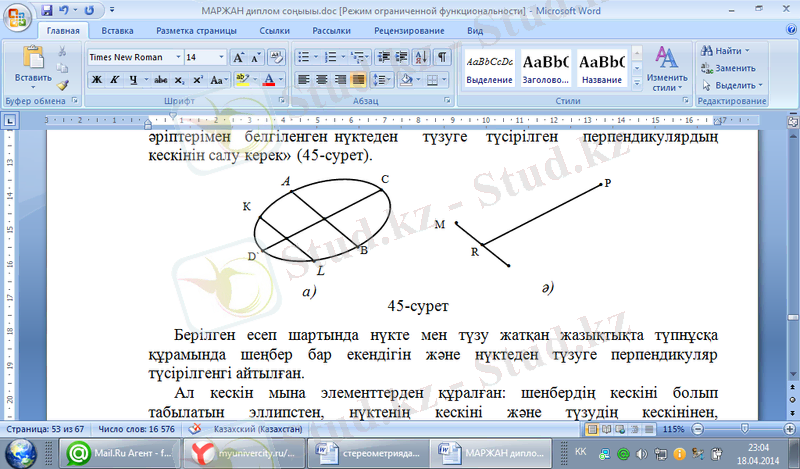
Берілген есеп шартында нүкте мен түзу жатқан жазықтықта түпнұсқа құрамында шеңбер бар екендігін және нүктеден түзуге перпендикуляр түсірілгенгі айтылған.
Ал кескін мына элементтерден құралған: шенбердің кескіні болып табылатын эллипстен, нүктенің кескіні және түзудің кескінінен, Перпендикулярдың кескінін салу керек.
Шенбер көмекші рөл атқарады, оның кескінін еркін түрде эллипс етіп кескіндей отырып метриканы анықтайды.
Жазық фигураларды салу есептері, егер оларды анықтайтын элементтердің кескіні мен метрикасы берілген жағдайда мынадай есептің келтірілуі мүмкін.
Бір жазықтықта жатқан нүкте, түзу және шеңбер берілген. Сызбада эллипс осы шенбердің кескі болып табылады, ал Р берілген нүктенің МN түзудің кескіндері (2 сурет) . Нүктеден түзуге түсірілген перпендикулярдың кескінін салу қажет.
Шешуі Эллипстің МN түзуіне параллель болатын АВ диаметрін жүргіземіз. АВ диаметріе түйіндес СD диаметрін жүргіземіз. Р нүктесінен СD диаметріне параллель жүргізілген РR түзуі ізделінді перпендикуляр болып табылады.
Дәлелдеу Шындығында:
1) Түпнұсқадан
 СОВ және
СОВ және
 РRN бұрыштарды өзара перпендикуляр және бірдей бағытталған қабырғалардың бұрыштарының кескіні болып табылады;
РRN бұрыштарды өзара перпендикуляр және бірдей бағытталған қабырғалардың бұрыштарының кескіні болып табылады;
2) АВ және СО диаметрлері өзара туйіндес болғандықтан
 СОВ бұрышы тік бұрыштың кесіндісін береді;
СОВ бұрышы тік бұрыштың кесіндісін береді;
3) Сызбада
МNАВ
және РRСD болғандықтан
 РRN тікбұрышыты Р нүктесінен
МN
түзуіне түсірілгeн перпендикулярдың кескінін береді.
РRN тікбұрышыты Р нүктесінен
МN
түзуіне түсірілгeн перпендикулярдың кескінін береді.
2. 2 Кеңістік фигурасының кескіні
Айталық, α жазықтығында F' кеңістік фигурасының F толық кескіні болсын. Демек, аффиндік R'={ О', А'
 , А'
, А'
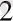 , А'
, А'
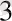 } реперінің кескіні болатын, жалпы жағдайдағы нүктелердің реттелген { О, А
} реперінің кескіні болатын, жалпы жағдайдағы нүктелердің реттелген { О, А
 , А
, А
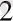 , А
, А
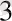 } төрттігі бар болады. Әрі F' түпнұсқасын анықтайтын барлық нүктелер, түзулер мен жазықтықтар кескіндеуде берілген болып табылады. F кескінін метрикалық анықталған ету үшін, ОА
} төрттігі бар болады. Әрі F' түпнұсқасын анықтайтын барлық нүктелер, түзулер мен жазықтықтар кескіндеуде берілген болып табылады. F кескінін метрикалық анықталған ету үшін, ОА
 кесінділерінің шын ұзындығы мен А
кесінділерінің шын ұзындығы мен А
 ОА
ОА
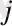 бұрыштарының шын шамаларын білу керек. Олай болса, жалпы жағдайдағы кеңістік фигурасының F толық кескінін салу үшін параметрлік сан
р
=6 болады.
бұрыштарының шын шамаларын білу керек. Олай болса, жалпы жағдайдағы кеңістік фигурасының F толық кескінін салу үшін параметрлік сан
р
=6 болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz