Модификацияланған деректерді қорғау

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

Кіріспе.
Курстық жұысты жазудағы мақсатым:
ЭЕМ-де сақталған ақпараттар мен мәліметтерді компьютерлік вирустардан қорғауды,деректерді сақтауды,тұтас ақпараттарды тексеруді,қалыптастыруды хэш функциясы арқылы жүзеге асыруды ұғындыру болып табылады.
Курстық жұмыстың құрылымы:
кіріспе,бірінші бөлім,екінші бөлім,үшінші бөлім,қорытынды жане әдебиеттер тізімінен тұрады.
Бірінші бөлім:Модификацияланған деректерді қорғаудеп аталады.Бұл бөлімде ақпараттарды модификацияланған деректерден қорғау кешенді жүйелік шешімді талап етеді. Олар міндетті түрде сенімді аппараттық және бағдармалық қамсыздандыруды, ұйымдастырылған сұрақтарды, деректерді сақтауды, компьютерлік вирустардан қорғауды, тұтас ақпараттарды тексеруді және олардың қалыптасуын да толық талап етеді. Нақты ақпараттық жүйелерде, әрдайым елулі ықтималдық модификацияланған ақпарат болады. Модификацияланған деректерден қорғаудын ең бастысы, ақпаратты бұрмалаушы, деректерді табу. Көпшілік кездерде бұл деректерді табу күрделі тапсырмалардын бірі болып келеді. Модификацияланған бағдармаларды ақпараттық жүйелерде пайдаланудын салдары, үлкен экономикалық шығындарға алып келуі мүмкін.
Ақпараттың тұтастығының бұзылуының себептері - сенімсіз аппараттық әдістерді ақпараттық технологияда пайдалану, сыртқы электромагниттық сәуленің әсері, табиғи кедергілердің каналдық байланысқа ықпалы, операторлар мен программистердің қателігі, компьютерлік вирустармен және бұзушылардың әрекеті. Осы себептердің көпшілігі абайсыз қателіктердін пайда болуына жол ашады. Бұл әдейі компьютерлік жүйеге енгізілген бағдарлама немесе арнайы жасалған вирус арқылы жүзеге асады. Бұзушы ақпараттық ресурстарға рұқсатсыз кіру мүмкіндігіне ие болу арқылы, электрондық құжаттарға өзгеріс енгізе алады, технологиялық бағдармаларды модификациялауға, дерекқордан ақпаратты жоюға немесе қосымша ақпарат енгізе алады. Бұзушы мақсатты өзгеріс енгізу барысында, модификацияны табу механизмін ескеру мүмкін, кей жағдайларда қасақана жасалған іс-әрекет кездейсоқ деректердің модификациялуына әкеп соқтыру мүмкін, мысалы, құпияланған деректерді модификациялау барысында. Егер мақсатты модификацияны табу тапсырмасы жүзеге асырылса, онда сол уақытта кездейсоқ бұрмалаушы ақпаратты табу тапсырмасыда орындалады.
Ақпараттық тұтастықты тексерудін әдіс-тәсілдерінің бірі - эталонды көшірмені сақтау, оны салыстыру үшін пайдаланады. Алайда, бұндай рәсім тұтас деректерді үлкен көлемде тексеруді қажет етеді, ол уақыт кідірісін туғызады, сондықтан бұл жүйе арнаулы оқиғаларда пайдаланады. Технологиялық тәсілдердің кейбіреулері бақылау соммасын есептеуде қиын заңдылықтарға негізделген. Көлемді деректер үшін бақылау соммасы есептеледі, былайша айтқанда эталондық күйде қалыптасқан. Осы эталонды бақылау соммалары ақпараттың тұтастықты тексеру үшін кестелерге жазылады. Ең бастысы енді екі көлемді деректі салыстырудың қажеті жоқ. Тұтастық жолмен салыстырылып тексеріледі, мысалы, 64-биттық, 128-биттық немесе 256-биттық бақылау соммасы арқылы.
Бұндай бақылау соммалар қорғаныстық бақылау соммалары(ЗКС) деп аталады. Оны есептеу үшін міндетті түрде күрделі заңдарға негізделген және мағналық шығу кодна байланысты әр бит хабарларға ықпал етуін қамтамасыз ететін алгоритмді пайдалану қажет. ЗКС-ны есептеу барысында, нақты тұтас ақпараттық қауіптерге және модификацияланған деректердің табылмау дәрежесіне тәуелдене отырып, әркелкі алгоритм түрлері қолданылады. ЗКС-ны есептеуде негізгі екі алгоритм түрлері:
oo Құпиялар ( немесе қолданыстағы құпия кілт)
oo Ашық (немесе кілтсіз)
Бастапқысы құпия кілтті пайдаланады немесе өз құпия болып табылады. Екіншісі ешқандай жасырын элементерді пайдаланбайды және әлуетті бұзушыларға белгілі. ЗКС-ны табу барысында бірінші немесе екінші алгоритмді пайдалану, шешілуші бақылау тапсырмаға тәуелді.
Ашық алгоритм негізінде бұзушы ЗКС-ның эталондық мағынасын табуы мүмкін, сонымен қатар модификацияланған хабарламаны алу мақсатында өте үлкен сандық тәжірибені жүзеге асыра алады. Егер m-биттық ЗКС бұндай тәжірибелік санында 2m мүмкіндігінше (12) ие болады, егерде бұзушы өзіне қажетті модификацияланған хабарды тапса. Демек, егер көрсетілген қауіп көкейкесті және әлуетті болса, бұзушы үлкен есептеуіш қорларға кіре алады, m96 қолдану мағынасын ұсынады.
Әртүрлі бақылау соммалары имотовставка деп аталады, олар салыстырмалы аз өлшемді және берілген шифромәтінде біріктіріле отырып, өзіндік кей қосымша ақпаратты ұсынады. Имитовставка келесі итеративті формула арқылы есептеледі
I = Ek ( Mi+ Si-1)
бұнда К - құпя кілт, Mi - шығыр (блок) деректірінің жиынтығы, бұнда кей шифрлы міндеттердің Е, i=1,2,..., n. көмегімен өзгерген хабарламалар жіктеледі.
Егер имитовставка ұзындығы m-бит пайдаланса, онда мүмкіндігінше деректердің модификация орны қабылдау жақпен табылмайды, 2-m құрайды. Көптеген практикалық кездерде m=64 ұғымы немесе тіпті m=32 имитостойканы қабылдауды қамтамасыздандырады.
1. 2 Хэш-функция
ЗКС-ның маңызды түрі хеш-функцияболып табылады, кілтсіз ЗКС-ға қарасты. Хеш-функцияны кейде криптографиялық бақылау соммасы деп те атайды. ЭЦП жүйесінде сандық саусақ ізін қолдануына байланысты, аз көлемдіден (128, 160 немесе 265 бит) электрондық құжатта үлкен көлемге (108 бит) дейін ЗКС-ның өзге алгоритм түрлеріне қарағанда қатал талаптар қойылады. Хеш-функция келесі талаптарды қанағаттандыруды қажет етеді:
oo Хеш-функция үшін дәлел еркін хабарлама ұзындығында болу мүмкін
oo Хеш-функция мағынасы тіркелген дәрежеге ие
oo Хеш-функция тиімді есептеуіш болып табылады
oo Хеш-функция криптографилық тұрғыдан берік болып келеді
Тиімді есептеу хеш-функция алгоритмының бағдармалық немесе аппараттық жүзеге асу барысында жетерліктей жоғарғы өндіргіштік қасиетке ие болуын білдіреді. Хеш-функция беріктілігі бойынша, ЗКС-ның әртүрлі нұсқаларына қарағанда, біраз жоғары талаптарды алға тартады. Хеш-функцияның ерекше талаптары, шабуыл қатары ЭЦП-ға негізделген хеш-функцияда пайдаланушы шабуылдарға байланысты. Дербес жағдайларда аталмыш шабулдар хатшы көмегімен екі құжатты сұрыпту мүмкіндігін өз алдына ұсынады; жария және модификацияланған хеш-функцияда бірдей мағнаға ие.
Бұл ретте ұйғарылатын жай - шабуылшы өте үлкен есептеуіш қорларды пайдалану мүмкін, мысалы, милиондаған процессор мен реттік жадтын 1016 байт шабулын ұйымдастыру мүмкін. Мейлі Н хеш-функцияда бар болсада, ал М-еркін өлшемнің хабарламасы.
Есептеуіш орындалмайтын екі хабарламаның тапқышы M' мен M'' = M′, елулі мүмкіндігінше мына шарт орындалады Н(М′) = Н(М″).
Ол сонымен қатар коллизонды беріктіліктің қатал талабы деп те аталыды. Және де әлсіз коллизонды беріктіктің талаптарын қалыптастырады:
М, айтылмыш хабарламасы үшін, хеш-функция Н(М) тен, өзге хабарламаның орындалмайтын есептеуіш тапқышы M'' = M′, ол үшін елулі ықтималдықта мына шарт орындалады Н(М′) = Н(М).
Хеш-функция коллизияға беріктігі қатал мағынада да болса, сонымен бірге әлсіз ұғымдада берік болып табылалы. Бірақ хеш-функция, коллизияға беріктілігі әлсіз мағынада, әрдайым коллизияға беріктілігі қатал мағнада бола бермейді. Коллизияға хеш-функцияның төзімді болуы қажетті, бірақ жеткіліксіз. Жүйе қыйынқайтқыш деп аталады, егер мына шарт орындолса
Кездейсоқ тандап алынған ұғым үшін Н орындалмайтын есептеуші тапқыш хабарлама М, елулі мүмкіндігінше хеш-функция Н тең яғни Н=(М).
Жалпы айтқанда хеш-функция қиынқайтқыштық(труднообратимой) болу керек. Функция қиынқайтқыштық(труднообратимой) болуы мүмкін, бірақ коллизонды төзімді бола алмайды. Мысал ретінде жай санның үлкен модульді дискретті дәрежесінің келтіруін алуға болады: Y=x mod p, бұнда -бастапқы түбір шегерім жүйесіндегі р модульдегі. Бұндай кезде Ү есептеуішін табу қиын, Х ұғымы берілген Ү сәйкес болуы керек, алайда мұндай мағыналар төтенше көп, тіпті хеш-функция жағдайларында да орын алады.
Егер хеш-функция берік болса, онда дәлелдің (аргумента) кез келген өзгеруі барысында оның мағынасы жалған бейнеде өзгереді, әсіресе, (12) мүмкіндігінше m биттық еселенген векторының Н әрқайсысы өзгереді. Қиынқайтқыштық(труднообратимой) хеш-функцияға қарапайым шабуылдаушы - хабарлама терімі болып табылады. Берілген хеш-функцияның Н мағынасына ие. Әртүрлі мәтіннің (N) мөлшерін бағалайық, сол арқылы хеш-функцияны анықтаймыз. Хеш-функция мағынасында берілген мәтін мүмкіндігінше солардын арасында (12) болу керек. Мүмкіндігінше (вероятность) хеш-функцияда кейбір ерікті тандалған мәтіндер берілген Н ұғымына сай келмейді, 1-2-m тен. Мүмкіндігінше, хеш-функция ешбір N әртүрлі мәтіндердегі Н сәйкес келмейді, p' = (1-2-m)N. Мүмкіндігінше, хеш-функция, ен болмағанда, осы хабарламаның Н біреуімен сәйкес, ол мынаған тең:
p=1-p' = 1-(1-2-m)N.
Ньютонның бинома формуласын пйдалана отырып келесі шешімді аламыз
(1-x)=1-Nx+N(N-1)2!*x2-N(N-1)(N-2) 3!*x3...=1-Nx, қысқаша түрде,
P=N*2-m немесеN=p*2m

Егер p=12 болса, онда N2m[-1]. Осы уақытта m=64 ұғымы үшін, салыстырмалы есептеуіш қорға ие, кез келген шабуылшылар ұжымыие бола алады. M96 битті қиынқайтқыштық(труднообратимой) хеш-функция осындай шабуылдарға берік бола алады, әйтседе шабуылдың басқада нұсқалары бар ,олар m 128 ұғымын пайдалануды қажет етеді.
Хеш-функцияның құрылуынын бір тәсілі кейбір интеративті миханизмді базадағы беріктік шифрлаушы функциядағы Е мен m - биттік кіруі болып келеді:
Hi= E ( Hi-1 Mi ), i = 1, 2, ..., n,
мұнда Н0 - кейбір арнайы сандалған бастапқы ұғым, Mi - кілт ретінде пайдаланушы шығыр (блок) хабарламасы. Н=Нn ұғымы хеш-функция ұғымы ретінде былайша жазып көрсетуге болады Н=Н(Н0, М), бұл жерде Н0бастапқы параметрға Н - тың тәуелділігін байқаймыз. Бұндай сызбаларда хеш-функцияның беріктілігінің құрылуы, базалық интеративті функция Е берігінен жоғары тұрмайды. Яғни ол қажетті криптографикалық берік базалық функцияны негіздікке алады.
Егер берікті кілтсіз хеш-функция болса, онда ол қарапайым түрде кілтті хеш-функцияға өзгеріле алады. Кейбір танымды шығыр шифраларының көмегімен алынған хеш-функцияның шифрланған ұғымын қосымша пайдалану жеткілікті болып келеді.
1.3. Шығырдық өзгерістердің негізінде хеш-функцияның құрылуы
Хеш-функция дәлелі ерікті хабарлама ұзындығы болып табылуына байланысты, кейбір интеративті механизм түрінде хеш-функцияны құрастыру ынғайлы, деректік шығырлардың өзгеруінде хабарлама бөлінуі жүзеге асады. Өзгеріс бір ғана шығырда орындалуын, раундық (раундовой) өзгеріс деп аталса, ал функцияның нақтылануы - раундық хеш-функция. Осылайша кейбір раундық шығыр хеш-функциясы F екі аргументке тәуелді болу керек: бастапқы хеш-функцияның рауындық ұғымы Нi-1 және ағымдықшығыршықтыңMi.. Бұны мынандай түрде жазуға болады:
Hi = F (Hi-1, Mi), i=1, 2,..., n,
мұнда Н0 - кейбір арнайы сандалған бастапқы ұғым. F шығырлық өзгеріс ретінде пайдаланылуы мүмкін, мысалы, шығырлық шифр немесе кейбір қиынқайтқыштық(труднообратимой) функция. Hi қолданылуы үзілісті айқас деп аталады. Ол шығыршықтың деректерге ағымдық қадамдарының өзгеру нәтижесінде тәуелділікті туғызады.
Жетерлік мөлшерде берік шығырлық шифрлардың әркелкі үлгілерін ұсына отырып, хеш-функцияның жасалуына деген қызығушылық шығырлық алгоритм негізінде жүзеге асады. Шығырлық шифрге негізделген қарапайым кешенді сызба Рабин сызбасы деп аталады. Ол келесі формула түрінде сипатталады:
Hi = EMi(Hi-1), i=1,2,...,n,
бұл жерде индекс ретінде параметр көрсетілген, кілт ретінде пайдаланған. Хеш-функцияға әмбебапты шабуыл Рабин сызбасы бойынша құрастырылған. Бұл шабуыл ортасында қиысу деп аталады.. Аталмыш шабуыл әмбебапты деп аталуы, оның рауындық өзгерістін нақты көрінісіне тәуелсіз болып келуінен. Аталмыш шабуылшы шифрланған функцияны m 128 шығыс көлемінде шектейді.
Өзге сызбаларда хеш-функцияның құрылымы рауындық өзгерістердін құрамында бөлшектік жинақтықтын екі модульінде қосымша пайдаланады. 9.1 суретінде бұндай рауынттық өзгерістердің үш нұсқасы көрсетілген. Сонымен қатар бұл сызбалардын кешенділігінде де пайдаланылады.
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
Сур.9.1. Раундық хеш-функцияның жиынтық құрылымының сызба нұсқасы:
а- Е функциясының шығысындағы қосылуы, б-кілт үшін кірістегі қосылуы, в-Е функциясының кірістегі қосылуы
Әртүрлі сызбаларда А, В, және С параметрлері ретінде Hi, Мi-1 және Mi ұғымдары қолданылуы мүмкін. Көпсанды сызбаларының зертелуінің көрсеткіші бойынша, берік хеш-функция құрылуында, берік шифрды жеткілікті деп қарастырмайды. Құрылымның нақты сызбасы басты орынға ие. Берік хеш-функция болып, формулаға сәйкесінше m биттық шифрі m 128 беріктігіне негізделіп құрылғанны дәлелді. 9.1 кестесінде көрсетілген. Берілген кестедегі бірінші, бесінші және оншы нұсқалары 9.2 суретінде сызба түрінде дәлелденген. Кей кезде сызбалық көрсеткіште тек қана i-дың есептеуіш қадамы беріледі.
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
Сур.9.2. 9.1 кестесіндегі 1(а), 5(б) және 10(в) нұсқаларына сәйкесінше құрастырылған, хеш-функцияның сызбасы
Кесте1.1
Берік шығырлық Е (Hi-1 және Mi параметрлерін пайдалану кезінде) функциясына негізделіп, хеш-функцияның сызбалық құрылуының қолданылуы.
№пп
Формула
1
Hi=E*H(i-1)(Mi)+Mi
2
Hi=E*H(i-1)(Mi+Hi-1)+M(i)+H(i-1)
3
Hi=E*H(i-1)(Mi)+Mi+H(i-1)
4
Hi=E*H(i-1)(Mi+H(i-1))+Mi
5
Hi=E*Mi(H(i-1)+H(i-1)
6
Hi=E*Mi(Mi+H(i-1))+Mi+H(i-1)
7
Hi=E*MiH(i-1)+Mi+H(i-1)
8
Hi=E*Mi(Mi+H(i-1)+H(i-1)

Hi-1, Мi-1 және Miпараметрлерін пайдалана отырып, рауындық хеш-функция нұсқаларының көпшілігі осыған негізделіп құрастырылу мүмкін. Бұндай сызбаларда бір тізім артық пайдаланылады, алайда олар берік сызба құрылуына сантүрлікті береді. Бірбағытты шығырлық функцияны қолдану барысында, блоктық шифрдың орнына әдетте шығыс пен кіріс болады, яғни тұрақты рауындық өзгерістерде ( бұл жағдайда қосымша М0 ұғымын сұрыптуды талап етеді) Мi-1 ұғымын түрлі мақсатта қолданылуында, әртүрлі пайдаланған сызбалардың мөлшерінің азаюна әкеледі. Ереже ретінде бірбағытты функцияға кірісті (вход) енгізу онай, яғни 9.1 кестедегі ескертпені қолдануды рұқсат етеді.
Қосымша кіріссіз бірбағытқа негізделген хеш-функцияны құрастыру қызығушылықты туғызады. Бұндай нұсқалар 9.3 суретінде көрсетілген, мұнда кіріс функциясының өлшемі F тен m 128 битке екені айтылған.
... ... ... ... ... ... ... ... ... ... ... ... ..
Сур.9.3. Блоктық бірбағытты өзгеріске негізделіп, хеш-функцияның құрылу сызбасы
Бірбағытты функцияны берік блоктық Е алгоритіміне негіздеп құрастыруға болады. Мысалы, мына формулаға сәйкестіріп:
F(X) = X Ek(X)
мұнда К - кейбір тіркелген белгілі кілт. Берік Ekалгоритмі үшін берілген функциян айналдыру қиын, яғнибіз Ekшығысында тіркелген векторды білмегендіктен. Қиынқайтқыштық(труднообратимой) блоктық өзгеріс құрылымында осы сынды әдістер хеш-функцияны пайдалануда жүзеге асады. Біздің мысалда аргумент блоктық шифрлау функциясының шығыс мағынасында да, қосылу мағынасында да қолданылады. Бірбағытты функцияда аргументті қолдану, (тұтастай немесе бөлшектей) кейде өзгеріс параметрі ретінде де болып табылады.
Мiұғымын аргумент, ал Нi-1 ұғымын кілт ретінде қолдануда, 9.1 кестесінен бірінші сызбаны ала аламыз. Көрсетілген бірбағытты сызбасын пайдалану 9.3г суретінде берілген. 9.4а және 9.4б суреттеріне негізделіп сабақтаса өзгереді.
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
Сур.9.4. Хеш-функцияның құрылуындағы бірбағытты өзгеріс орнына Е шифрасын қолдану үлгісі.
9.3 суретінде көрсетілген соңғы сызба құрылымды еске түсіреді, бірақ бірінші жағдайда хеш-функция құрылымы бірбағытты өзгеріске негізделген, ал екіншісі - шифрлаушы негізінде. 9.3 суретінде көрсетілген, сызбада пайдаланған құрылымның әртүрлі элементері әркелкі қиыстырылуларда біріктірілуі мүмкін, алайда кейбір үйлесімдер әлсіз хеш-функциянын құрылуына алып келуі мүмкін. Мысалы 9.5 суретінде 9.3в жіне 9.3г суреттерінде қолданылған үйлесімді элементтердің нұсқалары берілген.
... ... ... ... ... ... ... ... ... ... ... ... .
Сур.9.5. Берік блоктық F өзгерістің қолданылуындағы беріксіз хеш-функция көрсеткіші
Соңғы сызбадан Hi = F(Mi Hi-1) Mi Hi-1 айқын байқалады. Берілген формуладан хеш-функцияның шығыс ұғымында сақталған хеширияланған хабарламаның қарапайым модификациясының ықтималдығын көру қиын емес.
М = (M1, M2,..., Mn) хабарламасы берілсін. Хеш-функцияның ұғымын осы хабарламадан есептей отырып, H1, H2, ..., Hn, рауындық хеш-функциясының барлық аралық ұғымын сақтауға болады. Енді кейбір Мi-1, Мi-2,..., Мj блоктық дерктерді модификациялаймыз және олардын орнына жаңа жүйелі блогті М'i-1, М'i-2,..., М'jаламыз. Бұл жаңа ұғымдардын Н'i-1, Н'i-2,..., Н'jпайда болуына алып келеді. Енді Мj+1 блогның орнына М'j+1 = НjН'j М'j блогын аламыз, одан мына ұғым шығады:
H(j+1)=F(M(j+1)+Hj)+M(j+1)+Hj=F(M(j +1)+Hj)+M(j+1)+Hj=H(j+1)
Хабарламадан хеш-функцияны есептеуден мына ұғым шығады:
M=(M1,M2,...,Mi,M(i+1),M(i+2),...,M j,M(j+1),M(j+2)...,Mn)
осылайша біз рауындық хеш-функцияның келесі жүйелік аралық ұғымын аламыз H1, H2,...,Hі-1, Hі, H'і+1, H'і+2,...,H'j, Hj+1,Hj+2,...,Hn. Осылайша біз берілген хабарлама мен хеш-функциядан, басқа хабарламаны онай таба аламыз. Бірақта кейбір кездейсоқ тандалған деректерден Н"ұғымын М" құжатын табу үшін, Н(М")=Н" шарты үлкен ықтималдықпен орындалатын күрделі есептеуіш болып табылады.
Осылайша, қарастырылған мысал қиынқайтқышты (труднообратимой) хеш-функцияны танытады, алайда әлсіз мағынада да коллизияға берік болмайды. Сонымен бірге F блоктық өзгеруінің кез келген бөлшегі үшін шабуыл құрылымы практикалық коллизияны онай табады. Бұл сызбаны дұрыс тандалмаған бірбағытты блоктық өзгерістермен, хеш-функцияның үлкен бөлшекті пайдалануымен өзгертуге болмайды.
II. Ортақ кездердегі коллизияны табу
Бірдей мағыналы хеш-функция екі әртүрлі хабарламаларды табу негізінде, қызмет атқарушы жүйедегі ЭЦП хеш-функциясы шабуылдарға берік болу керек. Практика барысында құжаттарды жазу үшін техникалық персонал дайындаған ақпарат ішінде әлуетті бұзушы болуы ықтимал. Егер хеш-функция коллизияны табуда берік болмаса, онда бұзушы хеш-функциясының бірдей мағынасына ие екі әртүрлі құжатты жасуы мүмкін. Аталмыш құжаттардың бірінің мазмұны қол қоюшымен келісімді. Қол қойылғаннан кейін бұл құжат сұрыпталған мағынаға ие екінші құжатпен алмасады. Жасанды құжат пен келісім тексерушіге жөнелтіледі. Бұл тексеріс барысында келісім оңды нәтиже беріп, ал сұрыпталған құжат ақиқат ретінде қабылданылады.
Егер хеш-функцияның салыстырмалы мағыналық өлшемі аз болса, онда өзгерілімнің сапасына, хэширияланған алгоритмнің қамсыздануына қарамастан, коллизия туылған күн парадоксына негізделген шабуыл көмегімен табылады. Туылған күн парадоксының жауабы келесі сұрақта қаралған. Кездейсоқ тандалған адамдар арасында 0.5 ықтималдығымен топтағы 2 адамның туылған күні сәйкес келу үшін топ саны қандай болу керек? Бұл топтағы адамдардың саны 20 адамды құрауы тиіс. Туылған күндерінің кездейсоқ сәйкестену ықтималдығы үшін жұптар p'=1356 құрайды, ал n топдағы адамдар n ( n-1 )2 n22 әртүрлі жұпқа ие. Бұдан келесі сарапшы жақындықты табу онай. 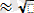Ең болмаса осы жұптардың бірі p p' n22 құрайтын туылған күндері сәйкестену ықтималдығына ие, бұдан p=12 үшін n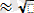1 p' аламыз.
Коллизияны табуда, туылған күндердің парадоксын қалай қолдануын қарастырайық. m-биттік шығыс ұғымымен Н хеш-функциясы берілсін. Әртүрлі N құжатты құрастырамыз M(1), i = 1, 2, ...N, және сәйкесінше H(i) хеш-функциясын табамыз. Егер хеш-функция жалған өзгерімділік берсе ( ал берік хеш-функция осындай қасиетке ие), онда алынған N құжаттары арасында бірдей H(i) екі ұғым табылмау ықтималдығын есептеу онай.
Алдымен коллизия санының аздығын ескеріп, бастапқы кезден жуықтауға сүйеніп отырған сараптаманы қарастырамыз. Кейбір H(1) ұғымын тандаймыз. Өзгелермен сәйкестенбеген ықтималдыққа тен
p(1) (1-2-m)N-1
Бұл қатнаста шығыс болжамы пайданылылады. Жаңа H(2) ұғымын аламыз. Өзгелеріне сәйкестенбеген ықтималға тен
p(2) (1-2-m)N-2
Хеш-функция әр кезде жаңа ұғым алуына байланысты, i-ді қадамында ұғымға сәйкессіз ықтималдықты аламыз
p(i) (1-2-m)N-1
Сәйкестену қадамын тексеруде, біз бар болғаны N-1орындауымыз керек. Олардың ешбіреуінде тен ұғымды ықтимал табылмауы, мына жүйені құрастырады:
p' (1-2-m)N-1*(1-2-m)N-1*...*(1-2-m)N- i*...*(1-2-m) =(1-2-m)Σ, мұнда Σ=1+2+...+(N- 1) = N(N-1)2
коллизия табу ықтималдығы (екі бірдей H(i) ұғымын) мынаны құрайды
p 1-p' = 1-(1-2-m)Σ 1- (1-Σ*2-m) N2*2-m-1
N2*2-m-1 (12) шартынан N(12) ұғымын анықтаймыз яғни коллизия барларымының (12) құрайды
N (12) 2m
Коллизия барларымын H(i) ұғымының көпшілігінде нақты есептеуші ықтимал, i = 1, 2, ... , N қарапайым түрде алынады. H(2) алайық. H(2) тен емес H(1) ықтимал, p(2) = ( 1-2-m ) жүйесіне тен. H(3) алайық. H(3) шартты H(1) және H(2) сәйкестенбеуі ықтимал, H(1) != H(2), p(3) = (1-2-m)*(1-2*2-m) жүйесіне тен. Бұл жүйені қарастыра отырып, p(N) ықтималдығы H(N) келесі ұғымдардың H(1), H(2), ... , H(N-1) біреуменде сәйкес келмейді, соңғы келтірілген ұғымдардың арасында тен ұғым жоқтығын шарттай отырып. p(N) = p(2) p(3) *...*p(N-1)* [1- (N-1)*2-m] аламыз. Осылайша коллизияның жоқтығы нақты ықтимал ұғым құрайды
p'=p(N)=(1- 2-m)*(1-2*2-m)*...*[1- (i-1)*2-m]*...*[1- (N-1)*2-m]=
-m).
Бұдан p'=1- p коллизия барларымын нақты анықтауға болады. Алайда, формула алу үшін, коллизия ықтималдығы мен N саны арасында көрнекі байланыс беріледі де, келесі жуықтау формаласын 1- х ≈ е-х пайдалануға болады. Мұндағы е-натуралды логарифмның негізі. Одан мына нәтиже алынады:
P=(i=N-1)П(i=1)(1-i*2-m)~(i=N-1)П(i =1)exp(-i*2-m)=exp(-(i=N1)Х(i=1)*i* 2-m)=exp[-N(N-1)*2-m-1]
Барлымның ықтималдығына ен болмағанда бір коллизия тең:
P~1-p`=1-exp[-N(N-1)*2-m-1]
Соңғы арақатнастан келесі ұғымды алу онай:
N2+N~2(m+1)ln(11-p)
N ұғымын N2 салыстырғанда мынандай жүйе пайда болады:
N2~2(m+1)ln(11-p),
N~2(m+1)ln(11-p).
p =0,5 үшін N (12) ≈ 1.17 * √2m бар. Осылайша бірінші нұсқадағы сияқты N (12) нақты есептік ұғымын шамамен шығарамыз. Туылған күн парадоксына негізделген тапсырма кезінде, кездейсоқ 23 адамның арасында 0,5 ықтималдықпен тек 2 адамның туылған күні сәйкес келеді.
N (12) үшін формуланы пайдалана және ескере отырып, Nэлементтерін сұрыптау тапсырмасы еңбек сыйымдылығының тәртібін NlnN, (12) ықтималдықпен коллизияны табу маңызында, қорларды (ресурс) бағалауға болады. 1.17*2m2 m-битті көлемдегі жадты талап ететінін айқындау онай. Сонымен қатар хеш-функцияны есептеуде 1.17*2m2 және N=1.17*2m2 санының сұрыпталуынын орындалуын қажет етеді. Хеширлау рәсімінің күрделілігін NnW ретінде бағалауға болады. Бұнда W-раунттық хеш-функцияны есептеудегі қажетті операцияның саны. Туылған күн парадоксына негізделген шабуылды қарастырғанда, m-64 битті ұғымында, ешқандай көрнекті алгоритмдер хеш-функцияның жоғары беріктілігін қамтамасыз ете алмайды.
Алайда, егер келісуші құжатқа қол қойар алдында кездейсоқ түзетулерді енгізсе, онда бұндай шабуылдар шектелуі мүмкін. Әрине бұл келісушіден қосымша іс-әрекетті талап етеді, ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.