Лаплас және Пуассон теңдеулері үшін дөңгелекте Дирихле, Нейман және Робин шеттік есептерінің шешім операторлары мен Грин функцияларын құру


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 38 бет
Таңдаулыға:
Ф-ОБ-001/033
Қазақстан Республикасы Білім және ғылым министрлігі
Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университеті
«Қорғауға жіберілді»
Кафедра меңгерушісі,
техн. ғ. д., профессор
Ә. Мұратов
«___»2012ж
Д И П Л О М Д Ы Қ Ж Ұ М Ы С
Тақырыбы: .
5В010900-«Математика» мамандығы бойынша
Орындаған: Хусанова С.
Ғылыми жетекшісі, Төребек Б. Т.
магистр оқытушы:
Түркістан 2014
Мазмұны
Кіріспе
Математикалық физика мен механиканың көптеген есептері эллипс тектес теңдеулер арқылы сипатталады [1-5] . Эллипс тектес теңдеулерге мысал ретінде Лаплас және Пуассон теңдеулерін қарастыруға болады.
Эллипс тектес теңдеулер үшін классикалық шеттік есептерге Дирихле, Нейман және Робен есептері мысал болады [1, 2] . Бұл есептер классикалық болғанымен олар түрлі сыныптарға тиісті. Себебі Дирихле және Робен есептері шартсыз шешіледі, ал Нейман есебінің шешімі бар болуы үшін шекаралық функцияға қосымша шарт талап етіледі, яғни Нейман есебі шекаралық шартында қатысқан функция қосымша шартты қанағаттандырғанда ғана шешілетін есеп болып табылады [2, 5] .
Жұмыстың мақсаты : дипломдық жұмыстың негізгі мақсаты Лаплас және Пуассон теңдеулері үшін радиусы бірге тең дөңгелекте берілген кейбір шеттік есептердің шешуші операторларын құру болып табылады.
Зерттеу әдістері : жұмысты орындау барысында Фурьенің айнымалыларды ажырату әдісі, дәрежелік қатарларды қосындылау әдістері және т. б. әдістер қолданылды.
Дипломдық жұмыстың құрылымы: дипломдық жұмыста бірлік дөңгелекте берілген Лаплас және Пуассон теңдеулері үшін негізгі шеттік есептердің шешуші операторларын құру мәселелері қарастырылады.
Жұмыстың негізгі бөлімі екі тараудан тұрады.
Дипломдық жұмыстың бірінші тарауында екінші ретті дербес туындылы дифференциалдық теңдеулер классификациясы және Лаплас теңдеуінің дербес шешімдері, кейбір қасиеттері туралы қысқаша мәліметтер жазылған.
Екінші тарауда
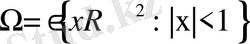 - дөңгелекте берілген Лаплас және Пуассон теңдеулері үшін негізгі шеттік есептердің шешімін құруға арналған. Алғашқы бөлімде
- дөңгелекте берілген Лаплас және Пуассон теңдеулері үшін негізгі шеттік есептердің шешімін құруға арналған. Алғашқы бөлімде
 ,
,
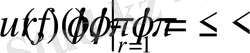 ,
,
түрдегі Лаплас теңдеуі үшін Дирихле есебі қарастырылып, оның шешімі
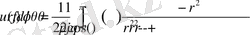 ,
,
көріністегі Пуассон интегралы арқылы жазылатындығы көрсетілген.
Сондай-ақ
 ,
,
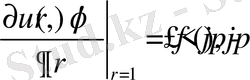 ,
,
түрдегі Нейман есебі қарастырылып, оның шешімі
 .
.
интегралы арқылы анықталатыны дәлелденген. Бөлімнің соңында Лаплас теңдеуі үшін үшінші шеттік есеп немесе Робин есебі деп аталатын
 ,
,
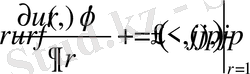 ,
,
есебі қарастырылып, шешімі
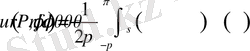
түрінде болатындығы келтірілген. Мұндағы
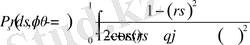 .
.
Жұмыстың екінші тарауы Пуассон теңдеуі үшін негізгі шеттік есептердің Грин функциясын құруға арналған. Мұнда алдымен
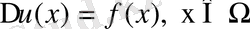 ,
,
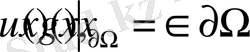 ,
,
(мұндағы f(x), g(x) - алдын ала берілген үзіліссіз функциялар) есебі қарастырылып, оның Грин функциясы

түрде анықталатыны көрсетілген. Сонымен қатар
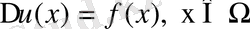
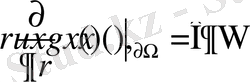
Нейман есебінің Грин функциясы

өрнегімен жазылатындығы дәлелденді. Сондай-ақ
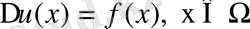
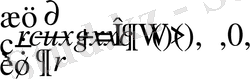
үшінші шеттік (Робен) есебінің де
көріністегі Грин формуласы есептелінді.
1 Эллипс тектес дербес туындылы дифференциалдық теңдеулер
1. 1 Екінші ретті дербес туындылы дифференциалдық теңдеулер классификациясы
Екі айнымалылы дифференциалдық теңдеулер.
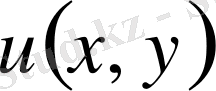 :
:
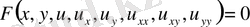 -
екінші ретті дербес туындылы теңдеу
деп аталады [1-3] .
-
екінші ретті дербес туындылы теңдеу
деп аталады [1-3] .
Бұл теңдеу жоғарғы ретті туындылары бойынша сызықтық деп аталады, егер мына түрде жазылса:
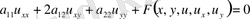 (1. 1. 1)
(1. 1. 1)
Мұндағы
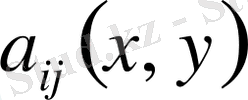 теңдеудің коэффициенттері. Егер осы (1. 1. 1) теңдеудің коэффициенттері
теңдеудің коэффициенттері. Егер осы (1. 1. 1) теңдеудің коэффициенттері
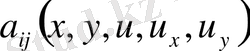 тәуелді болса, онда бұл теңдеу
квазисызықтық
деп аталады. Теңдеу сызықтық делінеді, егер мына түрде берілсе:
тәуелді болса, онда бұл теңдеу
квазисызықтық
деп аталады. Теңдеу сызықтық делінеді, егер мына түрде берілсе:
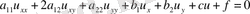 (1. 1. 2)
(1. 1. 2)
(1. 1. 2) теңдеу
сызықтық
деп аталады.
 -
коэффициенттері тұрақты болған жағдайда теңдеу
тұрақты коэффициентті
делінеді. Егер
-
коэффициенттері тұрақты болған жағдайда теңдеу
тұрақты коэффициентті
делінеді. Егер
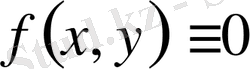 болса, онда (1. 1. 2) теңдеу
сызықтық біртекті
делінеді. Ал егер ол нольге тең болмаса, яғни
болса, онда (1. 1. 2) теңдеу
сызықтық біртекті
делінеді. Ал егер ол нольге тең болмаса, яғни
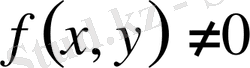 болса, онда ол
сызықты біртекті емес
деп аталады.
болса, онда ол
сызықты біртекті емес
деп аталады.
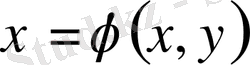 ,
,
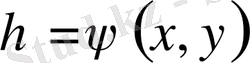 түрлендірулердің көмегімен теңдеуді жай түрде келтіреді.
түрлендірулердің көмегімен теңдеуді жай түрде келтіреді.
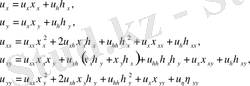
түрлендіру нәтижесінде мына түрге келтіреміз.
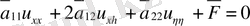
мұндағы
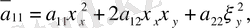
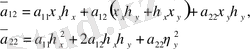
Егер бастапқы (1. 1. 1) теңдеу сызықтық болса, яғни
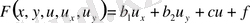 болса. Онда түрлендіру нәтижесінде
болса. Онда түрлендіру нәтижесінде
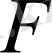 мына түрде жүреді.
мына түрде жүреді.
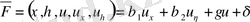
 және
және
 -ны
-ны
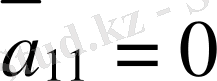 етіп таңдаймыз. Осыған байланысты
етіп таңдаймыз. Осыған байланысты
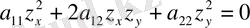 (1. 1. 3)
(1. 1. 3)
теңдеуі қарастырылады.
Бұл теңдеуге байланысты леммалар.
1-лемма.
Егер
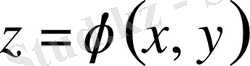 (1. 1. 3) теңдеудің дербес шешімі болса. Онда
(1. 1. 3) теңдеудің дербес шешімі болса. Онда
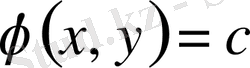 функциясы
функциясы
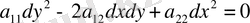 (1. 1. 4)
(1. 1. 4)
теңдеуінің жалпы шешімі.
2-лемма.
Егер
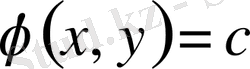 (1. 1. 4) теңдеудің жалпы шешімі болса, онда
(1. 1. 4) теңдеудің жалпы шешімі болса, онда
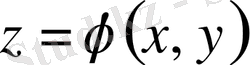 функциясы (1. 1. 3) теңдеуді қанағаттандырады.
функциясы (1. 1. 3) теңдеуді қанағаттандырады.
(1. 1. 4) теңдеу (1. 1. 1) теңдеудің характеристикалық теңдеуі делінеді, ал бұл (1. 1. 4) теңдеудің интегралдары (1. 1. 1) теңдеудің характеристикалары деп аталады.
1-лемманы дәлелдеу:
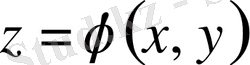 (1. 1. 3) теңдеудің шешімі
(1. 1. 3) теңдеудің шешімі
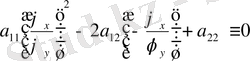
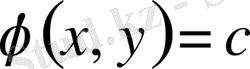 айқын белгілеген функцияны мына түрде жазуға болады.
айқын белгілеген функцияны мына түрде жазуға болады.
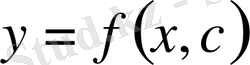 , онда
, онда
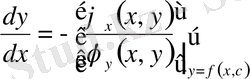
онда біз мынаны жазамыз.
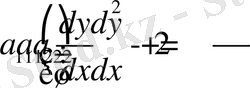
 .
.
Лемма дәлелденді. Характеристикалық теңдеу
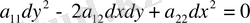
бұл теңдеуді мына түрге келтіреміз.
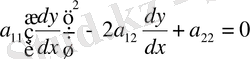
онда бұл теңдеудің екі шешімі бар.
1)
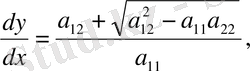
2)
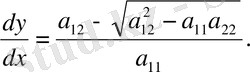
Сонымен
 нүктесінде біз мынадай анықтау қосамыз.
нүктесінде біз мынадай анықтау қосамыз.
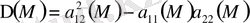
1.
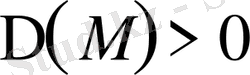 , онда дифференциалдық теңдеу
гиперболалық тектес
, себебі бұлардың екі нақты шешім шығады.
, онда дифференциалдық теңдеу
гиперболалық тектес
, себебі бұлардың екі нақты шешім шығады.
2.
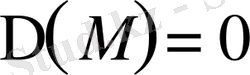 , онда дифференциалдық теңдеу
параболалық тектес.
, онда дифференциалдық теңдеу
параболалық тектес.
3.
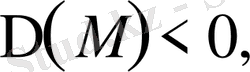 онда дифференциалдық теңдеу
эллиптикалық тектес
.
онда дифференциалдық теңдеу
эллиптикалық тектес
.
Егер жазықтықтың белгілі бір облысы қарастырылатын болса, онда әртүрлі нүктелерінде әртүрлі тектес теңдеулер болуы мүмкін немесе бір ғана тектес теңдеу болуы мүмкін. Облыстың әрбір нүктесінде бір ғана тектес теңдеу болса, онда осы облыста теңдеу сол түрде аталады.
Гиперболалық тектес.
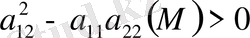 , онда характеристикалық теңдеудің екі жалпы шешімі болады.
, онда характеристикалық теңдеудің екі жалпы шешімі болады.
 ,
,
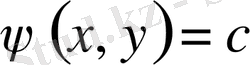 .
.
Енді мынадай алмастырулар жасаймыз.
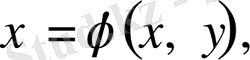
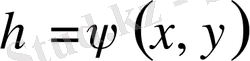 .
.
Сонда теңдеу мына түрге келтіріледі:
гипербола тектес теңдеудің жай түрі немесе канондық түрі.
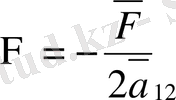
Практикада келесі түрдегі канондық теңдеулер де қолданылады. Алмастырулар жасаймыз.
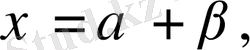
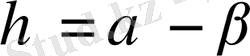 ,
,
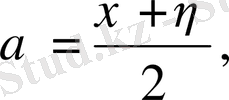
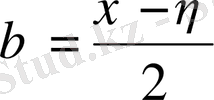
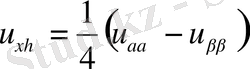 ,
,
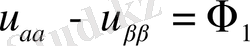
Екінші канондық түрі
 .
.
Параболалық тектес.
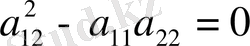 . Шешімі біреу-ақ болады.
. Шешімі біреу-ақ болады.
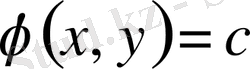 . Енді алмастыру жасаймыз.
. Енді алмастыру жасаймыз.
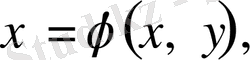
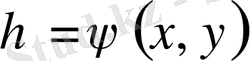 . Мұндағы
. Мұндағы
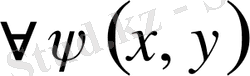
 -мен сызықты тәуелсіз функция.
-мен сызықты тәуелсіз функция.
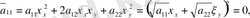
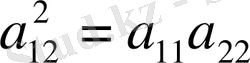
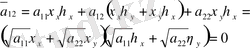
Сонымен бізде мынадай теңдеу шығады.
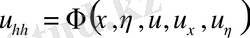 - Парабола тектес теңдеудің канондық түрі.
- Парабола тектес теңдеудің канондық түрі.
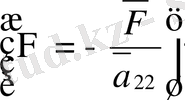
Элиптикалық тектес.
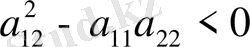 , бұдан, яғни характеристикалық теңдеуден комплекс түйіндес түбірлер шығады.
, бұдан, яғни характеристикалық теңдеуден комплекс түйіндес түбірлер шығады.
 ,
,
 .
.
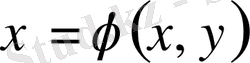 ,
,
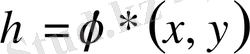 алмастырулар орындалады. Комплекс түйіндестен құтылу үшін келесі түрлендірулер жасаймыз.
алмастырулар орындалады. Комплекс түйіндестен құтылу үшін келесі түрлендірулер жасаймыз.
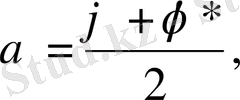
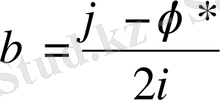
онда
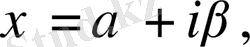
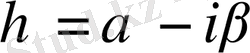 десек, онда біз мынадай теңдеу аламыз.
десек, онда біз мынадай теңдеу аламыз.
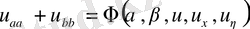 -Элиптикалық тектес теңдеудің жай түрі.
-Элиптикалық тектес теңдеудің жай түрі.
Қорытынды:
 гипербола тектес.
гипербола тектес.
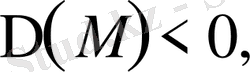
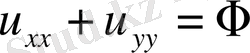 элиптикалық тектес.
элиптикалық тектес.
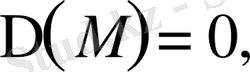
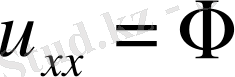 параболалық тектес.
параболалық тектес.
Көп айнымалылы екінші ретті теңдеу классификациясы
Сонымен біз мына теңдеуді қарастырамыз.
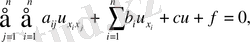


Екі айнымалыдан тәуелді жағдайдағыдай зерттеулер нәтижесінде мынадай жай түрдегі теңдеулерді аламыз.
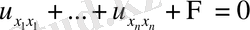 элипс тектес.
элипс тектес.
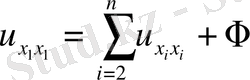 гипербола тектес.
гипербола тектес.
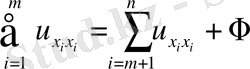 ,
,
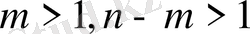 Бұл ультра гипербола тектес.
Бұл ультра гипербола тектес.
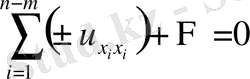 ,
,
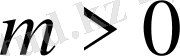 параболалық тектес.
параболалық тектес.
Тұрақты коэффициентті теңдеулердің канондық түрлері.
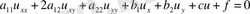 , мұндағы
, мұндағы
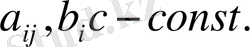
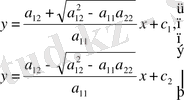 характеристикалық түзулер
характеристикалық түзулер
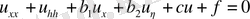 , эллипс тектес
, эллипс тектес
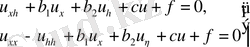 гиперболалық тектес.
гиперболалық тектес.
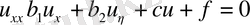 параболалық тектес.
параболалық тектес.
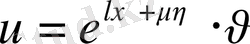 алмастыруын жасаймыз, сонда теңдеу мына түрге келеді.
алмастыруын жасаймыз, сонда теңдеу мына түрге келеді.
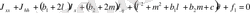
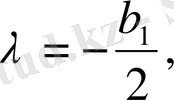
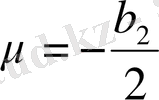 .
.
Сонда теңдеу мына түрге келеді.
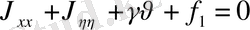 .
.
Мұндағы
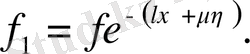
Осы сияқты түрлі комбинациялар арқылы келесі түрдегі теңдеулерді аламыз.
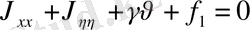 эллипс тектес.
эллипс тектес.
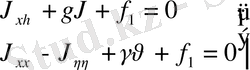 гипербола тектес
гипербола тектес
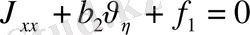 парабола тектес.
парабола тектес.
1. 2. Эллиптикалық тектес теңдеулер.
Әр түрлі стационарлы физикалық есептер процестер эллиптикалық теңдеулер есептеріне келтіріледі [1-6] . Жиі кездесеін теңдеу
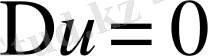
Лаплас теңдеуі.
Егер кеңістік бір өлшемді болса,
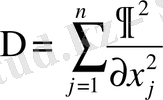
Т облысында берілген
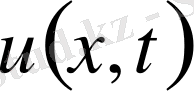 функциясы гармоникалық деп аталады. Егер осы облыста Лаплас теңдеуін қанағаттандыратын екі үзіліссіз дифференциалданатын және Лаплас теңдеуін қанағаттандыратын функциялар
гармоникалық функция класын
құрады.
функциясы гармоникалық деп аталады. Егер осы облыста Лаплас теңдеуін қанағаттандыратын екі үзіліссіз дифференциалданатын және Лаплас теңдеуін қанағаттандыратын функциялар
гармоникалық функция класын
құрады.
Лаплас теңдеуіне келтірілетін есептер.
Стационарлық өріс. Шеттік есептердің қойылуы.
Егер процес стационарлы болса, онда температураның таралуы тоқталады. Яғни
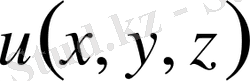
 -дан тәуелсіз келесі Лаплас теңдеуіне келеміз
-дан тәуелсіз келесі Лаплас теңдеуіне келеміз
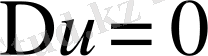
Егер жылу көздері бар болса, онда мына теңдеуге келеміз.
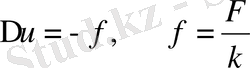 (1. 2. 1)
(1. 2. 1)
Мұндағы Ғ - жылу көздерінің тығыздығы, к - жылу өткізгіштік коэффициент. Біртекті емес Лаплас (1. 2. 1) теңдеуін көп жағдайда Пуассон теңдеуі деп те атайды.
 - көлемі
- көлемі
 дейтін бетпен қоршалсын. Онда Т-нің ішкі нүктелерінде
дейтін бетпен қоршалсын. Онда Т-нің ішкі нүктелерінде
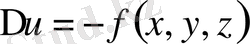
теңдеуін қанағаттандыратын
 функциясы іздестіріледі. Бұл біреуін қанағаттандыруын талап етіледі.
функциясы іздестіріледі. Бұл біреуін қанағаттандыруын талап етіледі.
І.
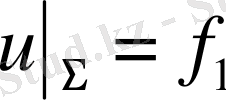 онда бұл
бірінші шеттік шарт.
онда бұл
бірінші шеттік шарт.
ІІ.
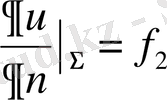 екінші шеттік шарт.
екінші шеттік шарт.
ІІІ.
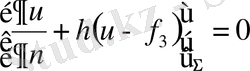 үшінші шеттік шарт.
үшінші шеттік шарт.
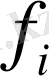 берілген функциялар
берілген функциялар
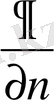 нормал бағыттағы туынды.
нормал бағыттағы туынды.
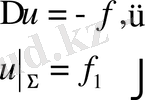
бірінші шеттік есеп немесе Дирихле есебі . Ал
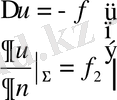
екінші шеттік есеп немесе Нейман есебі .
Егер
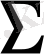 бетіне байланысты ішкі облыс қарастырылатын болса, онда шеттік есептер
іштей шеттік есептер
деп аталады. Ал егер
бетіне байланысты ішкі облыс қарастырылатын болса, онда шеттік есептер
іштей шеттік есептер
деп аталады. Ал егер
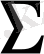 облысына байланысты ішкі емес сыртқы үктелер қарастырылатын болса, онда
сыртқы шеттік есептер
деп аталады.
облысына байланысты ішкі емес сыртқы үктелер қарастырылатын болса, онда
сыртқы шеттік есептер
деп аталады.
Қисық сызықты координаталардағы Лаплас түрлендірулері.
Лаплас ореаторының ортогонал қисық сызықты координаталарда қарастырайық. Сонымен, Декарт координататармен бірге қисық сызықты координаталар енгізілсін.
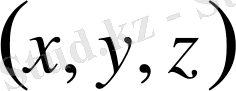
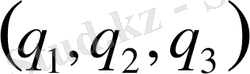
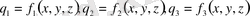
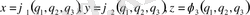
 беттері өзара ортогонал беттер деп есептелінеді.
беттері өзара ортогонал беттер деп есептелінеді.
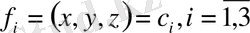 , АВ сызығында
, АВ сызығында
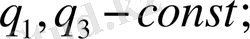 АС сызығында
АС сызығында
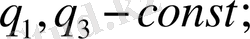 АD сызығында
АD сызығында
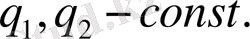
Онда бағыттаушы косинустар АВ, АС, АD сызықтарына бағыттаушы косинустар келесі шамаларға пропорционал.
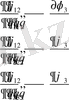
Онда беттердің қырларының ортогоналдығы былай жазылады.
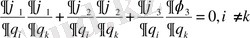
Сонда жаңа координаталардағы ұзындықтың элементі
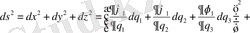
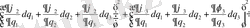
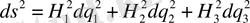
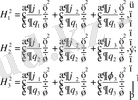
Әрбір қыры бойынша бір ғана айнымалы болатындықтан мыналарды аламыз.
 ,
,
 ,
,

Онда элементар көлем мынаған тең.
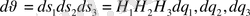
Кеңістікте векторлық өріс қарастыратын болсақ,
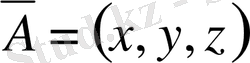 , онда бұның дивергенциясы мынаған тең:
, онда бұның дивергенциясы мынаған тең:
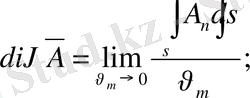
Ал егер өрісіміз потенциалды өріс болса
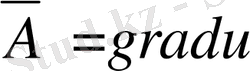 , онда біз мынаны аламыз.
, онда біз мынаны аламыз.
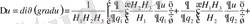
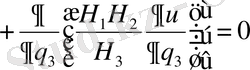
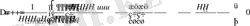 (1. 2. 2)
(1. 2. 2)
(1. 2. 2) қисық сызықты Лаплас теңдеуі. Осы теңдеудің екі дербес түрін қарастырайық.
Сфералық координаталар.
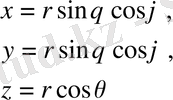
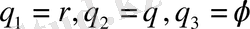 деп аламыз.
деп аламыз.
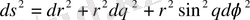
Онда бізде
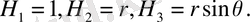
Сфералық координаталарда теңдеу былай жазылады.
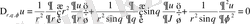
Цилиндрлік координаталар.
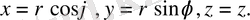
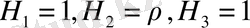
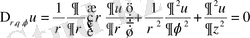 (1. 2. 3)
(1. 2. 3)
ал егер
 екі айнымалыға тәуелді болса, онда
екі айнымалыға тәуелді болса, онда
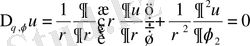 (1. 2. 3)
(1. 2. 3)
Бұл полярлық координаталардағы Лаплас теңдеуі.
Лаплас теңдеуінің кейбір шешімдері.
Сфералық немесе цилиндрлік симметрияларда берілген Лаплас теңдеулерінің шешімдерін оңай табуға болады. Бұл жағдайларда функция тек қана
 немесе
немесе
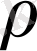 -дан тәуелді болады. Сонымен
-дан тәуелді болады. Сонымен
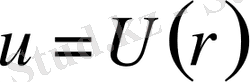 сфералық симметриялық жағдай. Сонда Лаплас теңдеуі
сфералық симметриялық жағдай. Сонда Лаплас теңдеуі
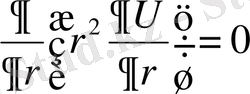 .
.
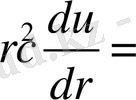 - тұрақты.
- тұрақты.
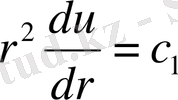
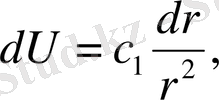
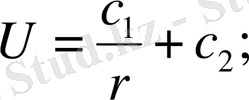
мұндағы с 1 , с 2 - кез келген
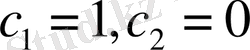 онда бұл мәнге тиісті шешім
онда бұл мәнге тиісті шешім
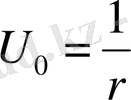
болады.
 шешімін Лаплас түрлендіруінің
фундамениалды шешімі
деп аталады.
шешімін Лаплас түрлендіруінің
фундамениалды шешімі
деп аталады.
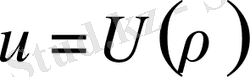 деп аламыз. Онда (1. 2. 3), (1. 2. 3) пайдаланып, дербес шешімдер аламыз.
деп аламыз. Онда (1. 2. 3), (1. 2. 3) пайдаланып, дербес шешімдер аламыз.
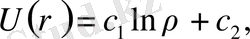
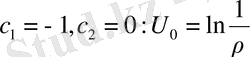
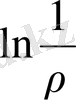 шешімді жазықтықтағы Лаплас теңдеуінің фундаменталдық шешім деп аталады.
шешімді жазықтықтағы Лаплас теңдеуінің фундаменталдық шешім деп аталады.
Комплекс айнымалы гармоникалық және аналитикалық функциялар.
Екі өлшемді кеңістіктегі Лаплас теңдеуінің шешімдерін комплекс айнымалы функциялы функциялар арқылы өрнектеу тиімді
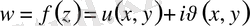
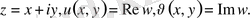
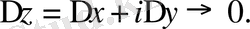
Өсімше нольге әртүрлі жолмен ұмтылады. Егер
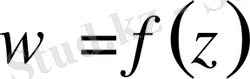 функциясы аналитикалық болса, онда
функциясы аналитикалық болса, онда
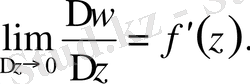
Функцияның аналитикалық болуы үшін Коши - Риман шарттарының орындалуы
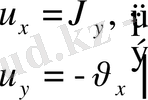
қажетті және жеткілікті.
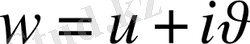 функциясын қарастырамыз.
функциясын қарастырамыз.
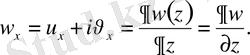
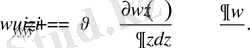
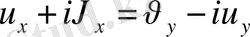 .
.
Егер қандай да бір G облысы берілсе, онда осы облыстың әрбір нүктесіндегі аналитикалық талап етілуі мүмкін. Бұндай жағдайда, яғни функция облыста аналитикалық болғанда кез келген ретті туындысы бар болады. Осы себепті аналитикалық функция дәрежелік қатарға жіктеледі. Көп жағдайда дәрежелік қатарға жіктелетін функцияны аналитикалық деп те атайды.
Кері радиус векторларды түрлендіру.
Радиусы
 сферада кері радиус векторларды түрлендіру деп кезкелген
сферада кері радиус векторларды түрлендіру деп кезкелген
 нүктесіне осы нүктенің радиусының жалғасында жатқан
нүктесіне осы нүктенің радиусының жалғасында жатқан
 нуктесінің
нуктесінің
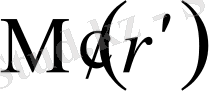 радиус векторлары
радиус векторлары
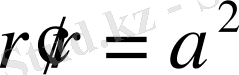 болатындай қатынасын айтады.
болатындай қатынасын айтады.
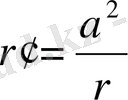
егер
 десе
десе
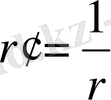
кері радиус векторларды түрлендіру.
Гормоникалық функция берілсін
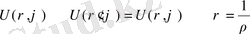
Дел осылайша
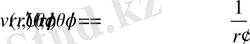
көз жеткізуге болады
Гармоникалық функциялардың жалпы қасиеттері
Гармоникалық функцияларды интегралдық түрде жазып жалпы қасиеттерін қарастырамыз. Мұнда максимум мән қағидасы ерекше орын алады. Осы қағида көмегімен бірнеше тұжырымдар делелденеді.
Грин формулалары. Шешімдердің интегралдық түрлері.
Остроградский формулаларымен Грин формулалары қортылады.
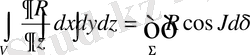
Остроградский формуласы. Мұндағы
 формуласы үзіліссіз функци
формуласы үзіліссіз функци
Бірнеше функция қарастыратын болсақ
жалпы турдегі Остроградский формуласы. Мұндағы
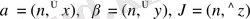
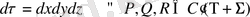
үзіліссіз және 1 реті дефференциялды функция.
Қандай да векторлық өріс берілсін
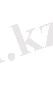
онда
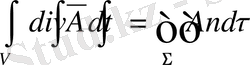 (2
\
)
(2
\
)
Ал вектордың нормаль векторға проекциясы
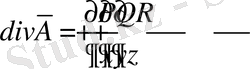
мұндағы
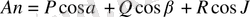 .
.
Остроградский формуласын пайдаланып Грин формуласын қорту.
 функциялары берілсін. Бұл функциялар
функциялары берілсін. Бұл функциялар
 облысында екі рет үзіліссіз дефференциалданады, ал
облысында екі рет үзіліссіз дефференциалданады, ал
 облысында бір рет дефференциолданатын болсын
облысында бір рет дефференциолданатын болсын
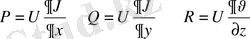
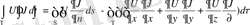 (1. 2. 4)
(1. 2. 4)
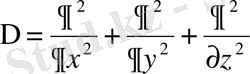
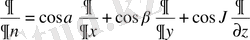
(1. 2. 4) -ші формуласы Гриннің 1-ші формуласы деп аталады.
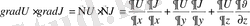
 және
және
 функцияларының орындарын алмастырсақ онда мынадай формула аламыз.
функцияларының орындарын алмастырсақ онда мынадай формула аламыз.
 (1. 2. 5)
(1. 2. 5)
(1. 2. 5) -ші формуланы Гриннің 2-шц формуласы деп аталады.
 облысы бірнеше беттермен шектелген күрделі облыс болуы мүмкін. Бұл жағдай да Грин формулалары өзгеріссіз қалады.
облысы бірнеше беттермен шектелген күрделі облыс болуы мүмкін. Бұл жағдай да Грин формулалары өзгеріссіз қалады.
 екі өлшемді кеңістік облысымыз
екі өлшемді кеңістік облысымыз
 контурымен шектелген болады.
контурымен шектелген болады.
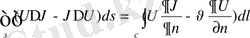
Мына функцияны қарастырайық

 ішкі нүктесі болсын.
ішкі нүктесі болсын.
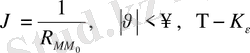
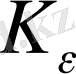 -шар центрі
-шар центрі
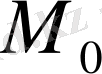 нуктесі болсын. Онда Гриннің 2-ші формуласын қолдансақ
нуктесі болсын. Онда Гриннің 2-ші формуласын қолдансақ
 мынадай теңдік шығады.
мынадай теңдік шығады.
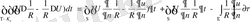
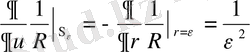
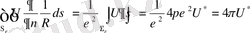
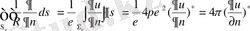
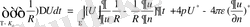
 ұмтылдырсақ :
ұмтылдырсақ :
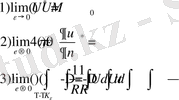
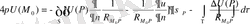 (1. 2. 6)
(1. 2. 6)
мұндағы
Егер
 нүктесі
нүктесі
 облысынан тыс жатса, онда
облысынан тыс жатса, онда
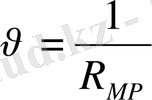 үзіллісіз және гарморикалық функция.
үзіллісіз және гарморикалық функция.
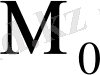 нүктесіне байланысты үш түрлі мүмкіндік бар.
нүктесіне байланысты үш түрлі мүмкіндік бар.
1)
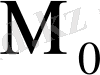 нүктесі облыстан сырт жатпайды.
нүктесі облыстан сырт жатпайды.
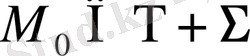
2)
3)

Осы мүмкіндіктерді ескерсек Гриннің негізгі формуласы (1. 2. 6) мына түрде жазылады.
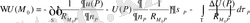
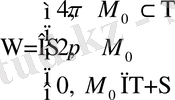
Гармоникалық функйия үшін
 , онда
, онда
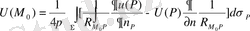
Гармоникалық функцияның ішкі нүктелеріндегі мәні беттегі мәндермен өрнектеледі.
Әрбір гармоникалық функция берілген облыста шексіз көп рет дифференциалданады. Жазықтық облыс үшін Грин функцияларын жазайық. Сонымен
 облысы берілсін.
облысы берілсін.
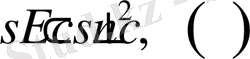
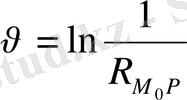
функциясын қолданып,
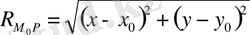
Гриннің негізгі формуласын жазайық.
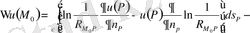
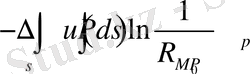
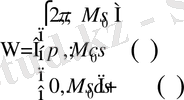
Гармоникалық функциялардың негізгі қасиеттері.
- Егер
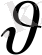 гармоникалық функция болса, Т облысында
гармоникалық функция болса, Т облысында
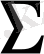 бетімен қоршалған, онда
бетімен қоршалған, онда
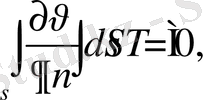
-
 Т облысында гармоникалық болса, ал
Т облысында гармоникалық болса, ал
 осы обьлыстың ішкі нүктесі болса
осы обьлыстың ішкі нүктесі болса
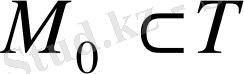 , онда
, онда
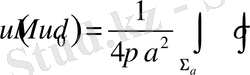
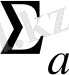 - сфера
- сфера
 центрі
центрі
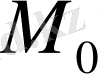 нүктесінде.
нүктесінде.
- Егер

 облысында үзіліссіз анықталған функция болса, Лаплас теңдеуін қанағаттандырса ішкі нүктелерінде
облысында үзіліссіз анықталған функция болса, Лаплас теңдеуін қанағаттандырса ішкі нүктелерінде
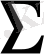 бетінде қабылданады. Бұны
максимум қағидасы
деп аталады.
бетінде қабылданады. Бұны
максимум қағидасы
деп аталады.
Салдар 1.
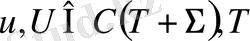
Егер
 - функциялары үзіліссіз функциялар болса,
- функциялары үзіліссіз функциялар болса,
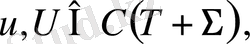 Т облысында гармоникалық болса, Т гармоникалық
Т облысында гармоникалық болса, Т гармоникалық
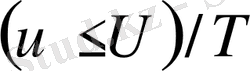
Салдар 2.
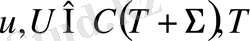 облысында гармоникалық болса және
облысында гармоникалық болса және
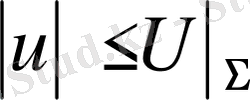 болса, онда
болса, онда
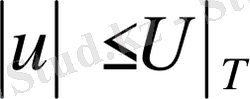 облысында
облысында
Бірінші шеттік есебінің шешімінің жалғыз және орнықтылығы.
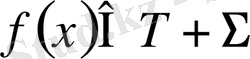
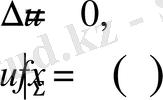
іштей бірінші шеттік есеп. Облыстың ішкі нүктелерінде теңдеуді қанағаттандырып, шекарасында берілген шартты орындайтын шешімін табу керек.
Теорема: Лаплас теңдеуі бірінші іштей шеттік есептің жалғыз шешімі бар.
Дәлелдеуі:
Есептің шешімі бар екендігі айқын. Осы шешімнің жалғыз екеніне көз жеткізейік. Керісінше
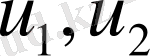 екі шешімі бар делік.
екі шешімі бар делік.
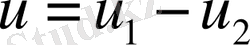 функциясы келесі талаптарды орындайды.
функциясы келесі талаптарды орындайды.
1.
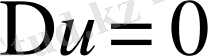 , Т;
, Т;
2.
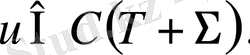
3.
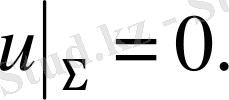
Функция
 үзіліссіз берілген облыста максималды, минималды мәндерді қабылдайды. Максимум қағидасы бойынша
үзіліссіз берілген облыста максималды, минималды мәндерді қабылдайды. Максимум қағидасы бойынша
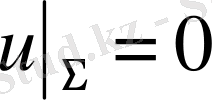 болғандықтан
болғандықтан
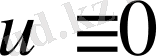 бүкіл облыста
бүкіл облыста
 .
.
2 Лаплас операторы үшін кейбір есептердің шешуші операторларын құру
2. 1 Лаплас теңдеуі үшін Дирихле, Нейман және үшінші шеттік есептердің шешімін құру
Айталық,

 екі өлшемді жазықтық болсын.
екі өлшемді жазықтық болсын.
Үзіліссіз функциялар класы
. D облысында анықталған, сол облыста өзі жане
k
-ші ретті туындысына дейін үзіліссіз болатын функциялар жиынын
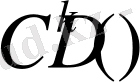 символымен белгілейміз.
символымен белгілейміз.
Гармониялық функция анықтамасы
. D облысында анықталған,
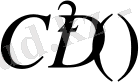 классына тиісті және
классына тиісті және
 үшін
үшін
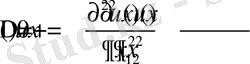
теңдігін қанағаттандыратын функцияны гармониялық функция деп атаймыз [1-4] .
Бұл жерде
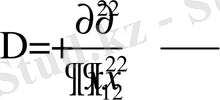
- Лаплас операторы, ал

теңдеуін Лаплас теңдеуі деп атайды [1-6] . ( Пьер-Симо́н Лапла́с (французша Pierre - Simon Laplace ; 23 наурыз 1749 - 5 наурыз 1827) - әйгілі француз математигі, физигі және астрономы. Оның атымен көптеген математикалық әдістер, теңдеулер, формулалар аталады. )
Айталық,
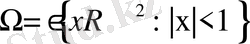
- центрі координаталар басында жататын радиусы бірге тең дөңгелек, ал,
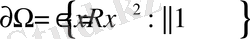
- оның шекарасы, яғни бірлік шеңбер болсын.
Бұл параграфта
 облысында
облысында
 ,
,
 (2. 1. 1)
(2. 1. 1)
Лаплас теңдеуін қанағаттандыратын

функциясының қасиеттерін зерттейміз.
Алдымен (2. 1. 1) -теңдеуді қанағаттандыратын

функциясын табу мәселесін қарастырайық.
 облысы дөңгелек болғандықтан, бұл мәселені полярлық координаттар жүйесінде қарастыру қолайлы болады.
облысы дөңгелек болғандықтан, бұл мәселені полярлық координаттар жүйесінде қарастыру қолайлы болады.
Бізге аналитикалық геометрия пәнінен декарттық координаталар жүйесінен полярлық координаталар жүйесіне көшу формуласы белгілі. Ол
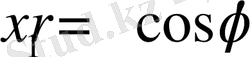 ,
,
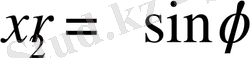
арқылы жүзеге асады. Керісінше, полярлық координаталар жүйесінен декарттық координаталар жүйесіне көшу формуласы
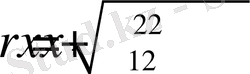 ,
,

арқылы анықталады. Осы формулаларды пайдаланып біз
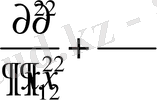
түрдегі Лаплас операторының полярлық координаталар жүйесіндегі көрінісін аламыз. Ол үшін бізге кейінгі есептеулерге
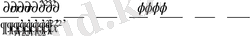
туындылардың мәндері қажет болады. Сондықтан осы туындыларды есептейік.
Бірінші
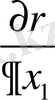 мәнін есептейміз. Онда
мәнін есептейміз. Онда
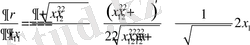
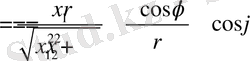
Ал,
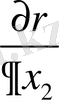 мәні
мәні
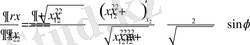
болады.
Енді екінші ретті туындыларын есептейміз. Яғни,
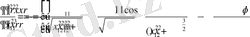
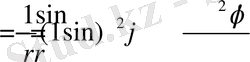 .
.
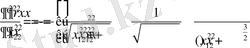
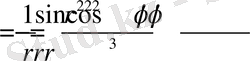 .
.
Ал, енді
 бойынша туындыларды есептейміз
бойынша туындыларды есептейміз
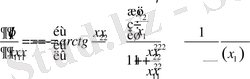
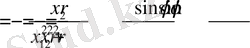 .
.
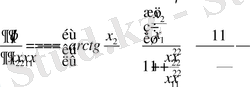
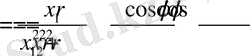 .
.
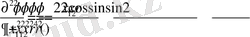
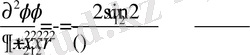 .
.
Енді полярлық координаттық жүйеде
 операторының қай түрде жазылуын анықтайық. Алдымен
операторының қай түрде жазылуын анықтайық. Алдымен
туындыларды есептейік :
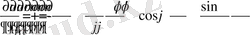
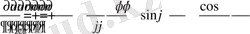
Екінші ретті туындыларды табамыз :

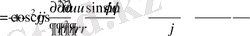
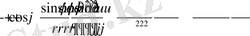
Демек,
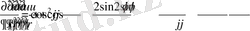
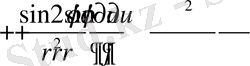
Осы сияқты
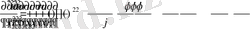
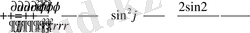

Нәтижеде
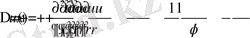
Демек полярлық координаттар жүйесінде (2. 1. 2) теңдеу
 (2. 1. 2)
(2. 1. 2)
түрінде жазылады .
Ендігі мақсат (2. 1. 2) - теңдеудің жалпы шешімін табу.
Ол үшін, алдымен бұл теңдеудің
 (2. 1. 3)
(2. 1. 3)
көріністегі шешімін табамыз. Бұл жерде
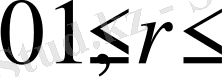

және

шарттары орындалады деп есептейміз.
Егер (2. 1. 3) -өрнекті (2. 1. 2) -теңдеуге қойсақ, онда
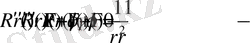
теңдігі келіп шығады .
Соңғы теңдікті
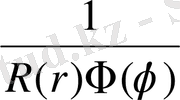
функциясына көбейтсек, онда
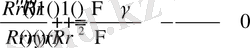
болады.
Бұдан
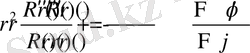 (2. 1. 4)
(2. 1. 4)
теңдігіні ие боламыз. (2. 1. 4) -теңдігінің оң жағы мен сол жағы бір-біріне тәуелді болмаған айнымалылардың функциялары. Онда
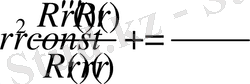
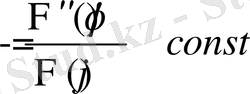
Бұл жердегі тұрақтыны
 деп белгілейік.
деп белгілейік.
Онда
 және
және
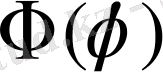 функциялары үшін мына теңдеулерге ие боламыз:
функциялары үшін мына теңдеулерге ие боламыз:
 (2. 1. 5)
(2. 1. 5)
 ,
,
 (2. 1. 6)
(2. 1. 6)
(2. 1. 6) -теңдеудің жалпы шешімі
болады. Егер

шарттын есепке алсақ, онда
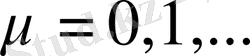 болуы керек.
болуы керек.
Олай болса (2. 1. 6) -есептің шешімі
 ,
,
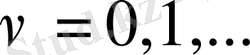 (2. 1. 7)
(2. 1. 7)
функциялары болады .
Осы
 -ларға сәйкес (2. 1. 4) -теңдеу
-ларға сәйкес (2. 1. 4) -теңдеу
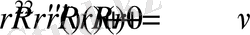 (2. 1. 8)
(2. 1. 8)
немесе
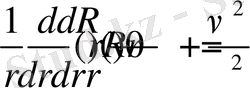
(2. 1. 8) -теңдеудің
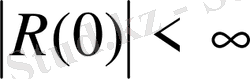
шартты қанағаттандыратын шешімдері
түріндегі функциялар болды .
Сонымен (2. 1. 1) теңдеуінің

түріндегі дербес шешімін алдық.
Біз қарастыратын функциямыз Ω облысында шенелген болуы қажет.
Онда
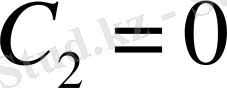 деп есептеу керек.
деп есептеу керек.
Олай болса,
Осы түрдегі функциялардың қосындысы тағыда (2. 1. 1) -теңдеудің шешімі болады. Оны теңдеудің жалпы шешімі деп есептеуге болады.
Сонымен, (2. 1. 1) - теңдеудің жалпы шешімі
 (2. 1. 9)
(2. 1. 9)
Бұл жерде

 - белгісіз тұрақтылар.
- белгісіз тұрақтылар.
Дирихле есебі.
Енді Ω облысында мына есепті қарастырайық
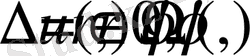 (2. 1. 10)
(2. 1. 10)
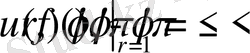 (2. 1. 11)
(2. 1. 11)
Бұл есепті Лаплас теңдеуі үшін Дирихле есебі деп атайды [1-6] . ( Иоганн Петер Густав Лежён-Дирихле (немісше Johann Peter Gustav Lejeune Dirichlet ; 13 ақпан 1805 - 5 мая 1859. Германия) - белгілі неміс математигі, математикалық талдау, функциялар теориясы және сандар теориясы салаларында өзіндік із қалдырған. )
Есептің шешімі деп
 классына тиісті болған және (2. 1. 10), (2. 1. 11) қанағаттандыратын
классына тиісті болған және (2. 1. 10), (2. 1. 11) қанағаттандыратын
 функциясына айтамыз.
функциясына айтамыз.
Осы есептің шешілуін зерттейік.
Есептің шешімін (2. 1. 9) қатар түрінде іздейміз.
Айталық,
 бұрышының функциясы ретінде берілген, периодты функция деп есептейік. Онда,
бұрышының функциясы ретінде берілген, периодты функция деп есептейік. Онда,
 функциясының Фурье қатарына жіктелуін аламыз
функциясының Фурье қатарына жіктелуін аламыз
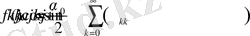 (2. 1. 12)
(2. 1. 12)
мұндағы
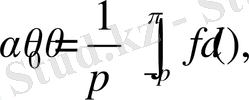
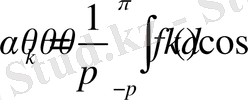 ,
,
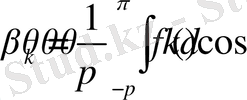 .
.
Егер (2. 1. 11) шекаралық шарт орындалады деп есептесек, онда (2. 1. 9) және (2. 1. 12) қатарларын салыстыра отырып, мынаны аламыз:
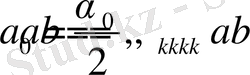
Сол себепті дөңгелек үшін Дирихле есебінің шешімін қатар түрінде аламыз
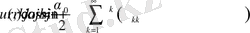 (2. 1. 13)
(2. 1. 13)
Пуассон интегралы.
Енді (2. 1. 13) қатарын қарапайым түрге келтірейік. (2. 1. 13) формулаға Фурье коэффициенттерін қоя отырып, қосынды және интегралдың ретін аусытыра отырып, мынаны аламыз:
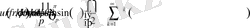
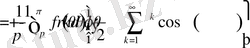 (2. 1. 14)
(2. 1. 14)
Енді

түрдегі формуланы пайдаланып келесі түрлендірулерді шығарамыз:
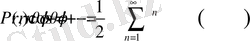


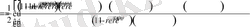
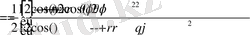
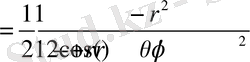
Алынған нәтижені (2. 1. 14) теңдеуге қоя отырып алатынымыз:
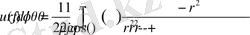 (2. 1. 15)
(2. 1. 15)
Дөңгелекте Дирихле есебінің шешімін беретін, бұл алынған формуланы Пуссон интегралы дейміз, ал интеграл астындағы өрнекті.
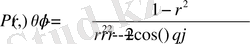
Пуассон ядросы дейміз ( Симеон Дени Пуассон (французша Simеon Denis Poisson , 21 маусым 1781 - 25 апреля 1840) - әйгілі француз математигі және физигі. Әйгілі француз математигі Жозеф Луи Лагранждың шәкірті. Сонымен қатар С. Д. Пуассон Мишель Шаль, Петер Густав Лежён-Дирихле, Жозеф Лиувилль, Сади Карно сияқты көптеген математиктердің ұстазы болып табылады. Пуассонның есімімен көптеген математикалық және физикалық формулалар мен заңдылықтар аталады. )
Пуассон интегралы
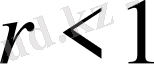 ұйғарымынан шыққан, ал
r=1
болғанда (2. 1. 15) өрнек мәнін жоғалтады.
ұйғарымынан шыққан, ал
r=1
болғанда (2. 1. 15) өрнек мәнін жоғалтады.
Бірақта
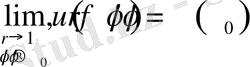
Олай болса, Пуассон интегралы тұйық облыста үзіліссіз функция болады.
Сонымен (2. 1. 15) формуласымен анықталған функция (2. 1. 10) - (2. 1. 11) Дирихле есебінің шешімі болады.
Шынында да
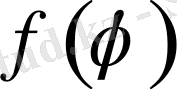 функциясы үзіліссіз болғанда Пуассон интегралы есептің шешімін беретінін дәлелдейміз.
функциясы үзіліссіз болғанда Пуассон интегралы есептің шешімін беретінін дәлелдейміз.
Кез-келген шектелген
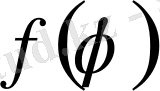 функциясы үшін
функциясы үшін
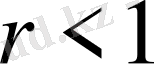 болғанда Пуассон интегралы Лаплас теңдеуінің шешімін береді.
болғанда Пуассон интегралы Лаплас теңдеуінің шешімін береді.
Егер
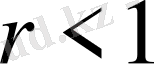 болса, онда Пуассон интегралы (2. 1. 13) қатарға тепе-тең келеді және кез-келген шектелген
болса, онда Пуассон интегралы (2. 1. 13) қатарға тепе-тең келеді және кез-келген шектелген
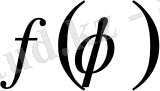 функциясы үшін
функциясы үшін

теңдігін қанағаттандырады.
Демек, біздің жағдайымызда u(r, ϕ) функциясы шекаралық шарттыда қанағаттандыратынын дәлелдеу ғана қалды.
Айталық,
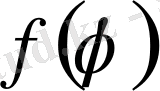 функциясына бірқалыпты жинақталатын, үзіліссіз дифференциалданатын функциялардың
функциясына бірқалыпты жинақталатын, үзіліссіз дифференциалданатын функциялардың

тізбегі берілсін, яғни
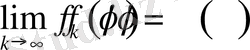
Егер
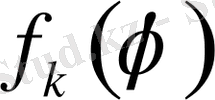 функцияларының тізбегін Дирихле есебінің шекаралық шартында қатысатын функциялар ретінде қарастырсақ, онда бұл функцияларға
функцияларының тізбегін Дирихле есебінің шекаралық шартында қатысатын функциялар ретінде қарастырсақ, онда бұл функцияларға
 гармониялық функцияларының тізбегін сәйкес келеді.
гармониялық функцияларының тізбегін сәйкес келеді.
 функциялары (2. 1. 13) қатар түрінде немесе (2. 1. 15) интеграл түрінде анықталады. Анықтама бойынша тізбектің бірқалыпты жинақтылығы мынаны білдіреді:
функциялары (2. 1. 13) қатар түрінде немесе (2. 1. 15) интеграл түрінде анықталады. Анықтама бойынша тізбектің бірқалыпты жинақтылығы мынаны білдіреді:
- кез-келген
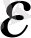 > 0
саны үшін сондай
> 0
саны үшін сондай
k
0
(
 ) >0
) >0
саны табылып
k>k
0
(
 )
)
болғанда
f
k
(φ) -f
k+ε
(φ) <
теңсіздігі орындалады.
Осыған сәйкес түрде
u
k
(r, φ) -u
k+ε
(r, φ) <
теңсіздігі де орындалады.
Осылайша анықталатын u k (r, φ) функцияларының тізбегі кейбір u (r, φ) функциясына бірқалыпты жинақталады.
Бұл u (r, φ) - шектік функция тұйық облыста үзіліссіз болады. u k (r, φ) функциялары
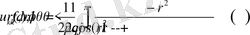
интеграл түрінде анықталады. Шартымыз бойынша
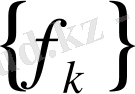 тізбегі
f
ке бірқалыпты жинақталады.
тізбегі
f
ке бірқалыпты жинақталады.
Сондықтан интеграл астындағы шекке көшуге болады.
Онда бұл тізбектің шегі болатын

функция кез-келген үзіліссіз
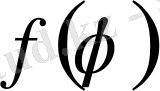 функциясы үшін Лаплас теңдеуінің шешімі болады және дөңгелектің шекарасында шекаралық шартты қанағаттантырады.
функциясы үшін Лаплас теңдеуінің шешімі болады және дөңгелектің шекарасында шекаралық шартты қанағаттантырады.
Лаплас теңдеуі үшін Нейман есебі.
Енді Ω облысында мына есепті қарастырайық
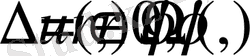 (2. 1. 16)
(2. 1. 16)
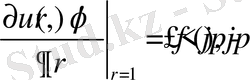 (2. 1. 17)
(2. 1. 17)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz