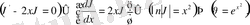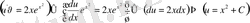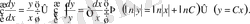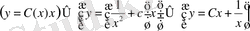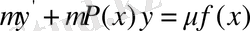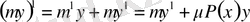Дифференциалдық теңдеулердің геометриялық есептерге қолданылуы: дипломдық жұмыстың ғылыми-әдістемелік бағалауы


Мазмұны
І. Кіріспе . . . 3
§ 1. Жай дифференциалдық теңдеулер . . . 4
- Бірінші ретті дифференциалдық теңдеулер . . . 4
- Теңдеудің геометриялық мағынасы . . . 5
§ 2. Айнымалылары ажыратылатын теңдеулер . . . 9
§ 3. Біртекті дифференциалдық теңдеулер . . . 18
§ 4. Сызықтық теңдеулер . . . 27
- Айнымалыларды алмастыру (Бернулли) тәсілі . . . 27
- Ерікті тұрақтыны вариациялау (Лангранж) тәсілі . . . 29
- Демеушілік көбейткіш тәсілі . . . 30
§ 5. Бірінші ретті дифференциалдық теңдеулердің ерекше
шешімдері . . . 37
Дифференциал теңдеулердің классификациясы және кейбір
есептердің шешімдері . . . 46
Қорытынды . . . 49
Пайдаланылған әдебиеттер . . . 51
Қожа Ахмет Ясауи атындағы Халықаралық Қазақ-Турік Университеті
Жаратылыстану және Медицина институты
Жаратылыстану факультеті
ЖМА-415 тобының студенті Файзиева Ироданың «Диффференциал теңдеулердің геометриялық есептерге қолданылуы» тақырыбындағы дипломдық жұмысына
Сын пікір
Файзиева Ироданың «Дифференциал теңдеулердің геометриялық есептерге қолданылуы» тақырыбындағы дипломдық жұмысы кіріспеден, 5 параграфтан, 14 суретттен және 1 кестеден, қорытынды және әдебиеттер тізімінен тұрады.
Бірінші параграфта жай дифференциалдық негізгі ұғымдарымен анықтамалары қарастырылған. Бірінші ретті дифференциалдық теңдеулермен теңдеуледің геометриялық мағыналары көрсетілген.
Екінші және үшінші параграфтада дифференциалдық теңдеулердің әр біріне, яғни айнымалылар ажыратылатын теңдеу, біртекті дифференциалдық теңдеулерге келтірілетін геометриялық есептер сурет және шешімдерімен толық көрсетілген.
Төртінші параграфта сызықтық теңдеулер айнымалыларды алмастыру (Бернулли) тәсілі, ерікті тұрақтыны вариациялау (Лагранж) тәсілі, демеушілік көбейткіш тәсілдері қолданып есептер көрсетілген.
Бесінші параграфта бірінші ретті диффенренциалдық теңдеулердің ерекше шешімдері, Клеро теңдеулеріне келтірілетін геометриялық есептер қарастырылған.
Жоғарыда айтылған пікірлерді есепке алып Файзиева Ироданың бұл жұмысы Қазақстан Республикасы Білім және Ғылым министрлігінің дипломдық жұмысына қойылған талаптарына сай және ол жоғары дәрежеде жасалынғаны және оны өте жақсы бағамен бағалауға болады деп есептеймін.
Пікір беруші: тех. ғ. к. профессор Темірбеков А.
1 § Жай дифференциалдық теңдеулер
1. Бірінші ретті дифференциалдық теңдеулер
1. 1 Негізгі ұғымдар. Тәуелсіз айнымалы
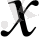 - ті, ізделінді функция
- ті, ізделінді функция
 пен оның туындыларын байланыстыратын теңдеуді жай дифференциалдық теңдеу дейді. Дифференциалдық теңдеуге енетін туындының ең жоғары ретін теңдеудің реті деп атайды.
пен оның туындыларын байланыстыратын теңдеуді жай дифференциалдық теңдеу дейді. Дифференциалдық теңдеуге енетін туындының ең жоғары ретін теңдеудің реті деп атайды.
Бірінші ретті дифференциалдық теңдеуді жалпы түрде
(1)
жазады. (1) теңдеу туындыға салыстыра шешілетін болса, ол былай жазылады:
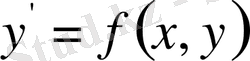 (2)
(2)
Дифференциальдық теңдеуді тепе - теңдікке айналдыратын кез келген
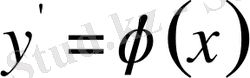 функцияны, оның шешімі деп атайды.
функцияны, оның шешімі деп атайды.
Егер
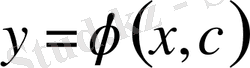
функциясы, тұрақты С-ның кез келген мәнінде (1) теңдеуді қанағаттандыратын болса, онда бұл шешімді (1) теңдеудің жалпы шешімі дейді.
 болғанда ізделінді функцияның
болғанда ізделінді функцияның
 мәні берілсе, бұл шартты бастапқы шарт деп, оны былай жазады:
мәні берілсе, бұл шартты бастапқы шарт деп, оны былай жазады:
немесе
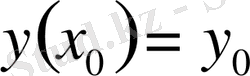
теңдеудің шешімінн анықтау процесін теңдеуді интегралдау деп атайды.
Теңдеудің жалпы шешімі
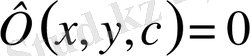 түрінде берілсе, оны теңдеудің жалпы интегралы дейді.
түрінде берілсе, оны теңдеудің жалпы интегралы дейді.
Ал, теңдеу шешімінің графигін интегралдық қисық деп атайды.
Коши теоремасы .
Егер
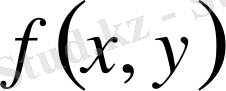 функциясымен оның дербес туындысы
функциясымен оның дербес туындысы
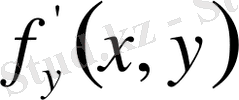
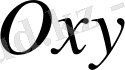 жазықтықтығының белгілі бір облысында анықталған және үзіліссіз болса, онда бұл облыстың қандай да бір ішкі нүктесі
жазықтықтығының белгілі бір облысында анықталған және үзіліссіз болса, онда бұл облыстың қандай да бір ішкі нүктесі
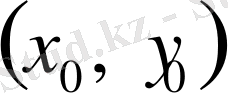 - дің кейбір төңірегінде (2) теңдеудің
- дің кейбір төңірегінде (2) теңдеудің
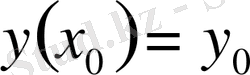 бастапқы шартты қанағаттандыратын жалғыз шешімі бар болады.
бастапқы шартты қанағаттандыратын жалғыз шешімі бар болады.
Бұл теорема (2) теңдеуі берілсе, оның шешімі бар және ол жалғыз ғана болатынын білу мүмкіндігін көретеді. Теореманың геометриялық мағынасы: D облысының әрбір ішкі нүктесі арқылы жалғыз интегралдық қисық өтеді.
Бастапқы шартты қанағаттандыратын теңдеудің шешімін іздеу есебін Коши есебі дейді.
Тұрақты С - ның анықталынған белгілі бір мәнінде жалпы шешімнен алынатын шешім (2) теңдеудің дербес шешімі делінеді.
2. Теңдеудің геометриялық мағынасы
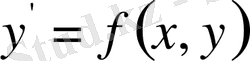 дифференциалдық теңдеуі берілсін және оның шешімі
дифференциалдық теңдеуі берілсін және оның шешімі
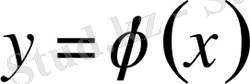 болсын.
болсын.
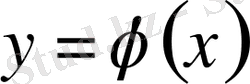 шешімінің графигі, әрбір нүктесі арқылы жанама жүргізуге болатын үзіліссіз интегралдық қисықты кескіндейді. Интегралдық қисықтың кез келген
шешімінің графигі, әрбір нүктесі арқылы жанама жүргізуге болатын үзіліссіз интегралдық қисықты кескіндейді. Интегралдық қисықтың кез келген
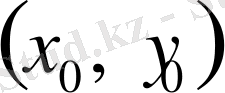 нүктесінде жүргізілген жанаманың бұрыштық коэффициенті
нүктесінде жүргізілген жанаманың бұрыштық коэффициенті
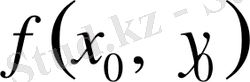 мәніне тең.
мәніне тең.
Сондықтан (2) теңдеуі
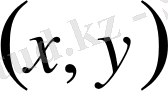 нүктесінің координаттары мен бұл нүктедегі интегралдық қисық графигіне жанаманың бұрыштық коэффициенті
нүктесінің координаттары мен бұл нүктедегі интегралдық қисық графигіне жанаманың бұрыштық коэффициенті
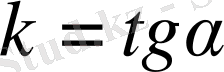 - нің арасындағы тәуелділікті тағайындайды.
- нің арасындағы тәуелділікті тағайындайды.
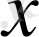 пен
пен
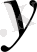 белгілі болса,
белгілі болса,
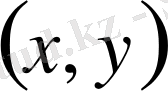 нүктесінде интегралдық қисық жанамасының бағытын көрсетуге болады.
нүктесінде интегралдық қисық жанамасының бағытын көрсетуге болады.
Осындай нүктелердің геометриялық жиынын «тұрақты сына» деп атайды.
Интегралдық қисықтың әрбір
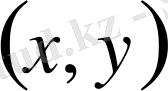 нүктесіне бұрыштық коэффициенті
нүктесіне бұрыштық коэффициенті
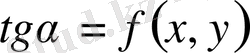 мәніне тең бағытталған кесіндіні орналастырсақ, берілген теңдеудің бағыттар өрісін аламыз.
мәніне тең бағытталған кесіндіні орналастырсақ, берілген теңдеудің бағыттар өрісін аламыз.
Сонымен,
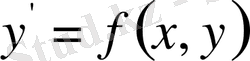 теңдеуі
теңдеуі
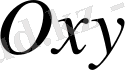 жазықтығында бағыттар өрісін анықтайды, ал оның шешімі әрбір нүктедегі жанама бағыты осы нүктедегі жанама бағыты осы нүктедегі өріс бағытымен дәл келетін интегралдық қисық болады екен.
жазықтығында бағыттар өрісін анықтайды, ал оның шешімі әрбір нүктедегі жанама бағыты осы нүктедегі жанама бағыты осы нүктедегі өріс бағытымен дәл келетін интегралдық қисық болады екен.
Берілген теңдеудің бағыттар өрісін жазықтықта құру арқылы интегралдық қисықтарды жуық шамамен кескіндеу мүмкін болады. Бұл әдіс «тұрақты сына» әдісі делінеді.
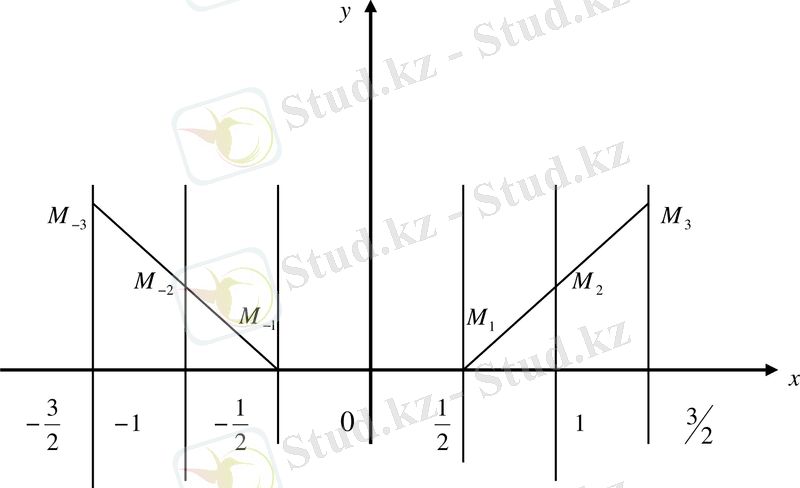
- мәселетеңдеуінің координат басынан өтетін интегралдық қисығын«тұрақты сына»әдісімен салу керек.
1-сурет
Шешуі:
 - паралеллель түзулері берілген тұрақты сынасы болады.
- паралеллель түзулері берілген тұрақты сынасы болады.
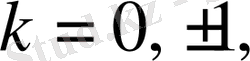
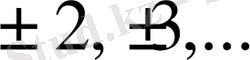 деп алып
деп алып
 ,
,
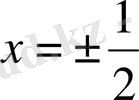 ,
,
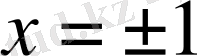 ,
,
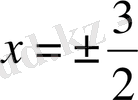 , . . . тұрақты сыналарын табамыз. Оларды салайық (1 - сурет) .
, . . . тұрақты сыналарын табамыз. Оларды салайық (1 - сурет) .
Буындарының бұрыштық коэффициенті . . . , -2, -1, 0, 1, 2, . . . болатын . . .
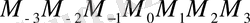 . . . сынық сызықтарын саламыз
. . . сынық сызықтарын саламыз
Мысалы,
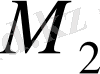 нүктесінде бұрыштық коэффициент
нүктесінде бұрыштық коэффициент
 теңдеуімен анықталады және т. с. с.
теңдеуімен анықталады және т. с. с.
Бұл сынық сызықтар теңдеудің интегралдық қисығын жуық түрде анықтайды.
Егер тұрақты сыналарды неғұрлым тығыз алсақ, онда соғұрлым интегралдық қисықты дәлірек алуға болатынын ескерте кетейік.
Енді геометрияға тиісті болған бір мысалды көрелік.
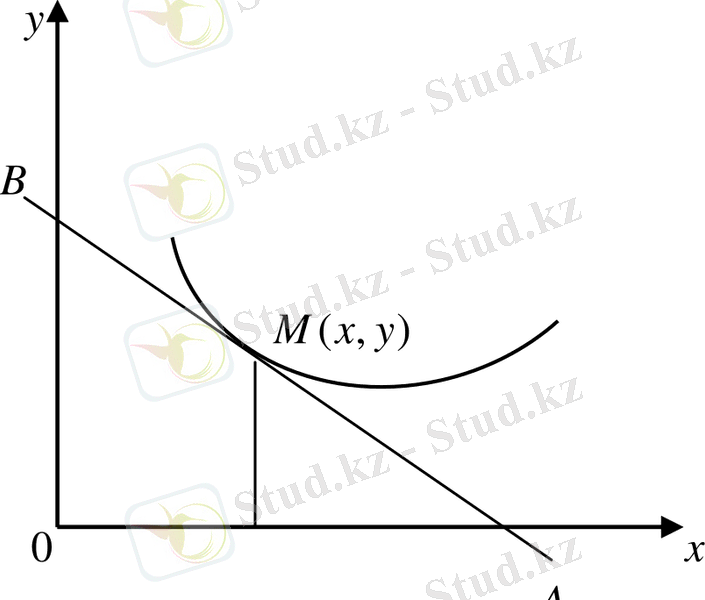
2- мәселе. Қисық сызыққа оның кез келген нүктесінен өткізілген жанаманың ординаталар өсінен ажыратқан кесіндісі ұрыну нүктесі ординатасының екі еселенгеніне тең. Сол қисық сызықтың теңдеуін табайық.
 Шешуі.
Ізделінді қисық сызықтан
Шешуі.
Ізделінді қисық сызықтан
кез келген
 нүкте аламыз
нүкте аламыз
(2-сурет) . М нүктеден өткізілген жа-
наманың теңдеуі
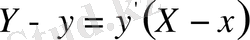
түрінде болады, мұнда
 - жана-
- жана-
ма нүктелерінің айнымалы координат-
тары,
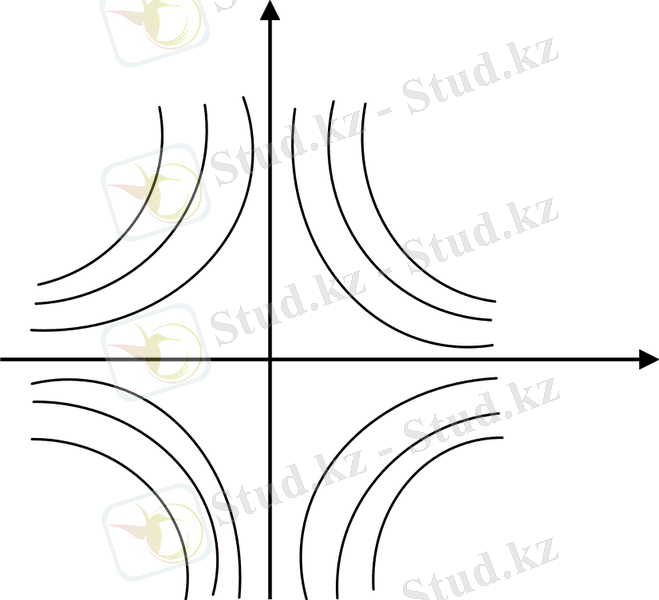
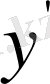 - ізделінді функцияның
- ізделінді функцияның
берілген нүктедегі туындысы. 2- сурет
 Жанаманың
Жанаманың
 өсінен ажыратқан
өсінен ажыратқан
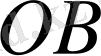 кесіндісін табу үшін
кесіндісін табу үшін
 деп аламыз.
деп аламыз.
Екіншіден, шарт бойынша
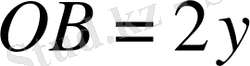 .
.
 кесінді үшін табылған екі өрнектеу салыстырып, 3-сурет
кесінді үшін табылған екі өрнектеу салыстырып, 3-сурет
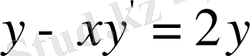
немесе
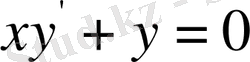
Бұл теңдіктің екі жағында
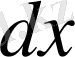 ке көбейтіп, оны дифференциал қатнасқан түрге келтіріледі.
ке көбейтіп, оны дифференциал қатнасқан түрге келтіріледі.
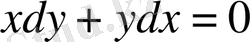 (*)
(*)
(*) теңдеудің сол жағы айнымалылар көбейтіндісінің дифференциалы
 , сондықтан (*) теңдеу
, сондықтан (*) теңдеу
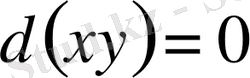
түрінде жазылады, мұнда
 ,
,
 - тұрақты сан.
- тұрақты сан.
 теңдеу ізделінді қисық сызықтың теңдеуін береді.
теңдеу ізделінді қисық сызықтың теңдеуін береді.
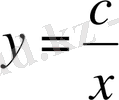 - қисық сызықтар әулетін, яғни асимптоталары координата өстері болатын тең өсті гиперболалар әулетінен құралған. (3- сурет) .
- қисық сызықтар әулетін, яғни асимптоталары координата өстері болатын тең өсті гиперболалар әулетінен құралған. (3- сурет) .
2 § Айнымалылары ажыратылатын теңдеулер .
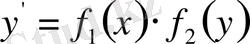 немесе
немесе
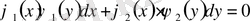 түріндегі теңдеуді
айнымалылары ажыратылатын теңдеу
деп атайды.
түріндегі теңдеуді
айнымалылары ажыратылатын теңдеу
деп атайды.
Шынында, теңдеудің айнымалыларын ажыратуға болады:
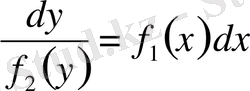 немесе
немесе
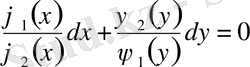
Бұл теңдеудің жалпы шешімі:
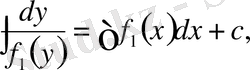 немесе
немесе
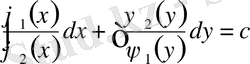
түрінде жазылады.
Егер айнымалылары ажыратылатын теңдеулерде
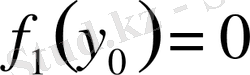
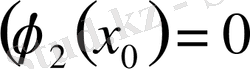 және
және
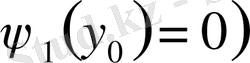 болса, онда ажырату нәтижесінде дифференциалдық теңдеудің
болса, онда ажырату нәтижесінде дифференциалдық теңдеудің
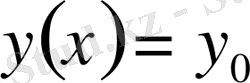
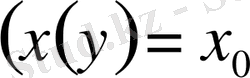 және
және
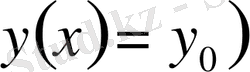 шешімдері жоғалуы мүмкін. Сондықтан теңдеуді айнымалыларды ажырату әдісімен шешуде көрсетілген шешімдер жалпы шешімнің құрамына енетінін тексеру керек. Егер ол шешімдер енбесе, онда оларды теңдеудің жалпы шешімінің құрамына енгізу керек.
шешімдері жоғалуы мүмкін. Сондықтан теңдеуді айнымалыларды ажырату әдісімен шешуде көрсетілген шешімдер жалпы шешімнің құрамына енетінін тексеру керек. Егер ол шешімдер енбесе, онда оларды теңдеудің жалпы шешімінің құрамына енгізу керек.
3-мысал.
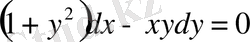 дифференциалдық теңдеудің шешімін табайық.
дифференциалдық теңдеудің шешімін табайық.
Шешуі:
Теңдікті
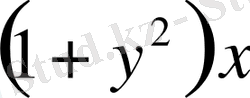 көбейтіндісіне бөлсек,
көбейтіндісіне бөлсек,
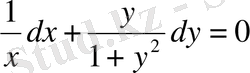 болады.
болады.
Сонымен, айнымалылар ажыратылды. Енді интегралдасақ,
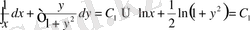
Потенциалдауға ыңғайлы болу үшін,
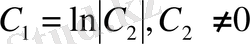 деп аламыз.
деп аламыз.
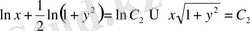 (*)
(*)
Берілген дифференциалдық теңдеудің
 шешімі болғандықтан ол шешім (*) түріндегі жалпы шешімге енбейтін болғандықтан
шешімі болғандықтан ол шешім (*) түріндегі жалпы шешімге енбейтін болғандықтан
 - ден басқа ноль мәнді қабылдайтын С параметрін енгіземіз. Сонда
- ден басқа ноль мәнді қабылдайтын С параметрін енгіземіз. Сонда
 шешімі, мына түрдегі
шешімі, мына түрдегі
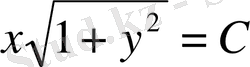 жалпы шешімге кіреді.
жалпы шешімге кіреді.
4-мәселе . Нормал ұзындығы мен нормал асты ұзындығының қосындылары тұрақты а санына тең болған қисық сызықты табу керек.
Шешуі:
Нормал асты ұзындығы
 , ал нормал ұзындығы
, ал нормал ұзындығы
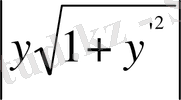 . Берілген шарт бойынша ізделінді функция
. Берілген шарт бойынша ізделінді функция
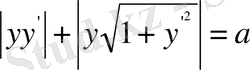
дифференциалдық теңдеуін қанағаттандаруы керек. Соңғы теңдеуден
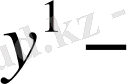 тапсақ:
тапсақ:
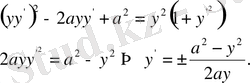
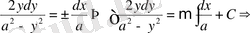
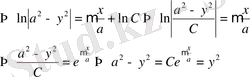
Мәселе шерты тек қана
 болғанда орындалады. Шынында да қисық сызықтар әулетінен табылады:
болғанда орындалады. Шынында да қисық сызықтар әулетінен табылады:
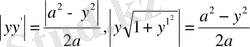
Сондықтан
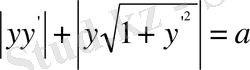 шартын қанағаттандыру үшін
шартын қанағаттандыру үшін
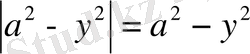 , яғни
, яғни
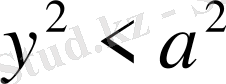 болуы керек, сондықтан тек қана оң мәндерді қабылдайды.
болуы керек, сондықтан тек қана оң мәндерді қабылдайды.
5-мәселе
.
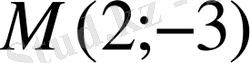 нүктеден өтетін және жанаманың бұрыштық коэффициенті болған сызықтың теңдеуін табу керек.
нүктеден өтетін және жанаманың бұрыштық коэффициенті болған сызықтың теңдеуін табу керек.
Шешуі: Мәселе шартында берілген:
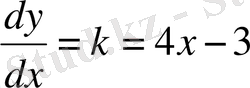 немесе
немесе
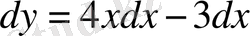
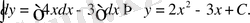
 және
және
 болғанда
болғанда
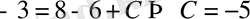 онда ізделінуіді функция
онда ізделінуіді функция
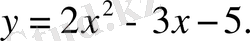
6-мәселе.
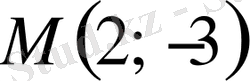 нүктеден өтетін және жанаманың бұрыштық коэффициенті
нүктеден өтетін және жанаманың бұрыштық коэффициенті
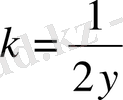 болған сызықтың теңдеуін табу керек.
болған сызықтың теңдеуін табу керек.
Шешуі: Мәселе шарты бойынша
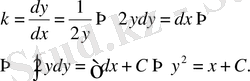
 ,
,
 болғанда
болғанда
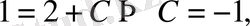
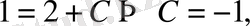 онда ізделінді функция
онда ізделінді функция
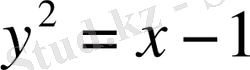
7- мәселе . Әрбір нүктесіндегі жанаманың бұрыштық коэффициенті жанасу нүктесінің абсциссасына пропорционал болатын қисықтың теңдеуін табу керек.
Шешуі. Мәселе шарты бойынша
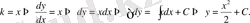
Ізделінді қисық параболалар әулеті болар екен.
8-мәселе.
Бағыттық сыналар тәсілін қолданып
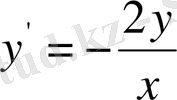 дифференциалдық теңдеуінің интегралдық қисығын жуықтап салайық.
дифференциалдық теңдеуінің интегралдық қисығын жуықтап салайық.
Шешуі.
Ол үшін алдымен
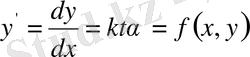 теңдікті пайдаланып бағыттық сыналар сызықтар жиынтығын табамыз:
теңдікті пайдаланып бағыттық сыналар сызықтар жиынтығын табамыз:
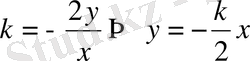
Демек, берілген дифференциалдық теңдеуге сәйкес бағыттық сыналар (изоклиндер) -бас нүкте арқылы өтетін түзулер жиынтығы болатындығын көреміз. Бұл түзулер бойындағы бағыттық өріс
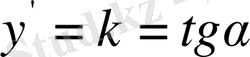 теңдігімен анықталады. Енді демеушісіне мәндер беру арқылы, сәйкес бағыттық сыналап түзуін тауып, оның бойында жатқан бағыттар өрісін пайдаланып ізделініп отырған интегралдық қисыққа (шешімге) жүргізілген жанамалардың бұрыштық коэффициенттерін
теңдігімен анықталады. Енді демеушісіне мәндер беру арқылы, сәйкес бағыттық сыналап түзуін тауып, оның бойында жатқан бағыттар өрісін пайдаланып ізделініп отырған интегралдық қисыққа (шешімге) жүргізілген жанамалардың бұрыштық коэффициенттерін
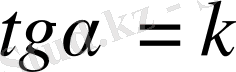 , яғни жанаманың
, яғни жанаманың
 өсімен жасайтын бұрыштарын анықтаймыз (кесте) .
өсімен жасайтын бұрыштарын анықтаймыз (кесте) .
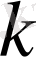
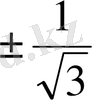
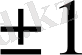
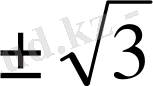
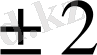
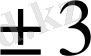


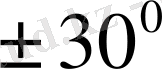
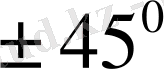
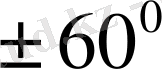
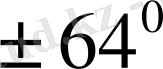
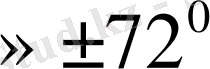
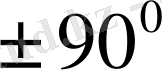
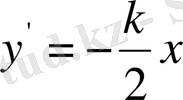
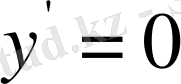
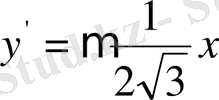
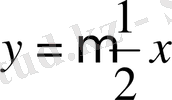
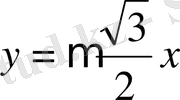

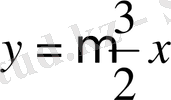

Келтірілген кестедегі мәліметтер бойынша бағыттар өрістерін құрып, одан жуықтап болса да сәйкес интегралдық қисықтарды саламыз.
9-мәселе.
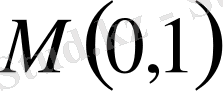 нүктеден өтетін және жанаманың жанасу нүктесінде бұрыштық коэффициентігі
нүктеден өтетін және жанаманың жанасу нүктесінде бұрыштық коэффициентігі
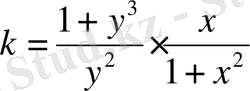 болға қисық сызықтың теңдеуін табу керек
болға қисық сызықтың теңдеуін табу керек
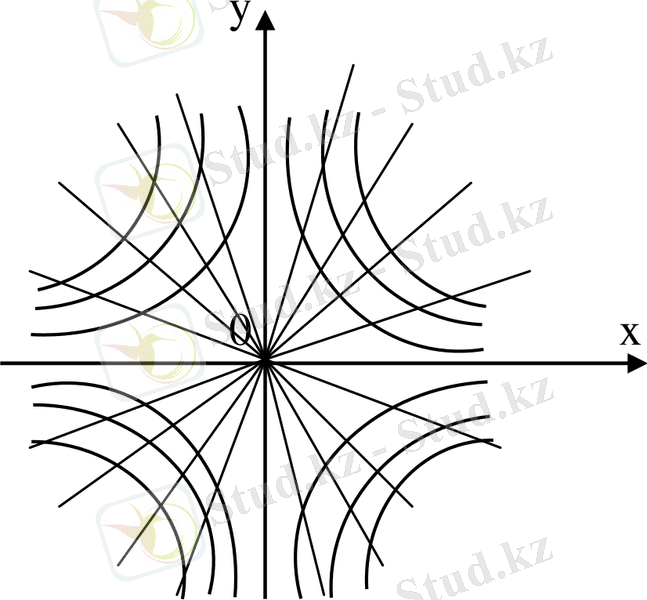
4-сурет
Шешуі.
Мәселе шарты бойынша

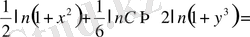
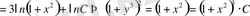
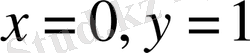 болғанда
болғанда
 Онда ізделінді функция
Онда ізделінді функция
10 - мәселе. Табу керек;
1) жанаманың бұрыштық коэффициенті жанасу нүктесіне тең болған қисық сызықты.
2) (2, 5) нүктеден өтетін қисықты.
Шешімі.
- Ізделінді қисық сызық әулетінің дифференциалдық теңдеуі
немесе
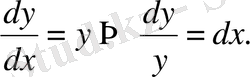 Сонғы теңдіктің екі жағында интегралдап табамыз:
Сонғы теңдіктің екі жағында интегралдап табамыз:
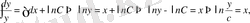

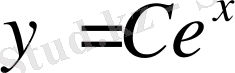
жоғарыдағы қасиетке ие болған қисық сызықтар әулеті.
2) С тұрақтыны табайық:
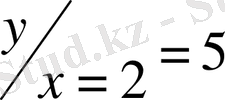 бастапқы шарт бойынша тапсақ:
бастапқы шарт бойынша тапсақ:
 Сондықтан (2, 5) нүктеден өтетін интеграл қисық
Сондықтан (2, 5) нүктеден өтетін интеграл қисық
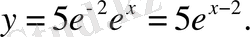
11- мәселе. Координаттар өстері арасында жайғасқан жанама кесіндісі жанасу нүктесінде тең екіге бөлінетін қисық сызықтар әулетінің теңдеуін табу керек. (3, 4) нүктеден өтетін қисызық сызық теңдеуін жазу керек.
Шешуі:
СМ=МВ, онда
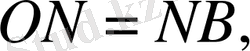
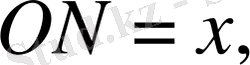
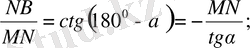
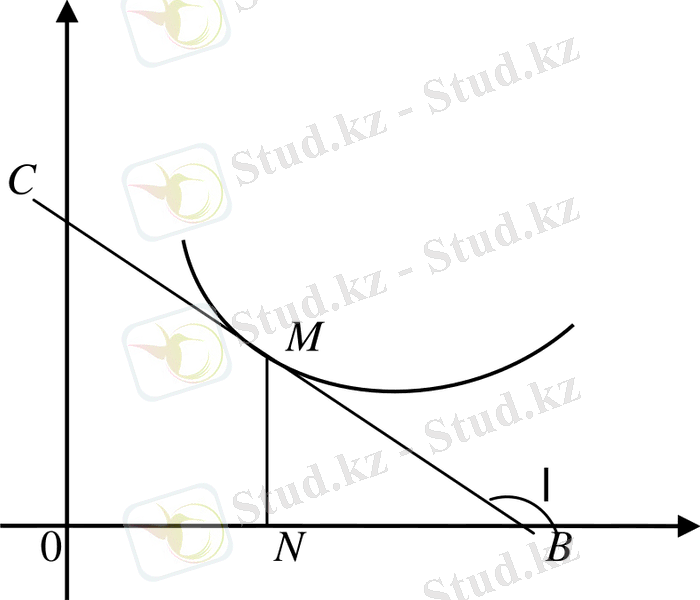
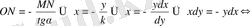
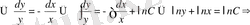
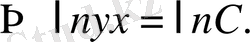
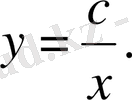
Ізделенді қисық сызық
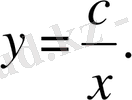
Бұл тең бүйірлі гиперболалар әулеті.
(3, 4) нүктеден, яғни
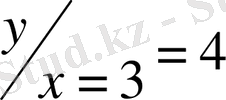 бастапқы 5-сурет
бастапқы 5-сурет
шартты қанағаттандыратын интегралды
қисық теңдеуін табу үшін С тұрақтының мәнін табуымыз керек.
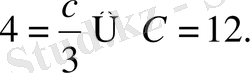
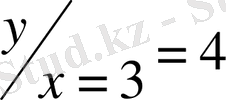 бастапқы шартты қанағаттандыратын қисық
бастапқы шартты қанағаттандыратын қисық
сызық теңдеуі
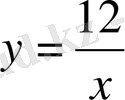 .
.
12- мәселе.
 нүктесінен өтетін және кез келген нүктесіндегі жанамасының координат осьтері арасындағы кесіндісі жанасу нүктесінде 2:3 (
нүктесінен өтетін және кез келген нүктесіндегі жанамасының координат осьтері арасындағы кесіндісі жанасу нүктесінде 2:3 (
 - өсінен бастап есептелінеуі) қатынасындай бөлінетін сызықтық теңдеуін табу керек.
- өсінен бастап есептелінеуі) қатынасындай бөлінетін сызықтық теңдеуін табу керек.
 Шешуі. Айталық
Шешуі. Айталық
 ізделінді функция,
ізделінді функция,
 қисықтың кез келген нүктесі,
қисықтың кез келген нүктесі,
 қисыққа жанама,
қисыққа жанама,
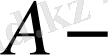 жанаманың
жанаманың
 өсімен,
өсімен,
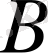
оның
 өсімен қиылысу
өсімен қиылысу
нүктелері.
 нүктесінің
нүктесінің
 осіндегі
осіндегі
проекциясы болсын (6- сурет. )
Жанаманың
 осінің оң
осінің оң
бағытымен жасайтын бұрышын
 деп белгілейік, онда
деп белгілейік, онда
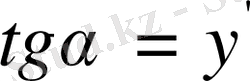 .
.
Екінші жағынан 6 - сурет бойынша 6-сурет
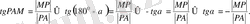
Алынған қатынасты
 нүктесінің ағымдық координаттары
нүктесінің ағымдық координаттары
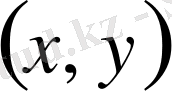 арқылы өрнектейік.
арқылы өрнектейік.
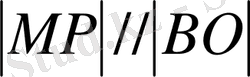 болғандықтан,
болғандықтан,
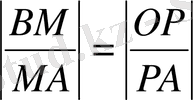 болады.
болады.
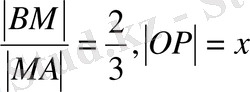 екендігін ескерсек,
екендігін ескерсек,
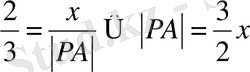 және
және
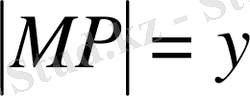
Демек,
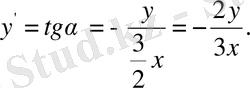
Бұл алынған теңдеу айнымалылары ажыратылатын бірінші ретті дифференциалдық теңдеу.
Айнымалыларды ажыратып интегралдасақ:
немесе
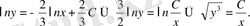
Бұл интегралдық қисықтар үйірінен
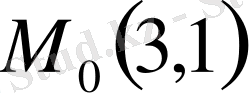 нүктесі арқылы өтетін қисықты таңдап аламыз. Ол үшін
нүктесі арқылы өтетін қисықты таңдап аламыз. Ол үшін
 ,
,
 мәндерін теңдеудің жалпы шешіміне қойсақ:
мәндерін теңдеудің жалпы шешіміне қойсақ:
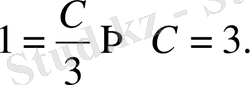 болады.
болады.
Демек, ізделінді қисықтың теңдеуі
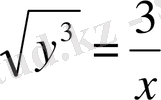 болады.
болады.
13- мәселе
.
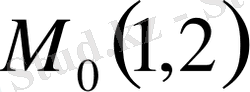 нүктесінен өтетін және кез келген нүктесіндегі жанаманың координат осьтерінің арасындағы кесіндісі жанасу нүктесінде
нүктесінен өтетін және кез келген нүктесіндегі жанаманың координат осьтерінің арасындағы кесіндісі жанасу нүктесінде
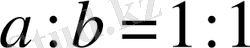 (
(
 -осінен бастап есептегенде) бөлетін сызықтың теңдеуін табыңыз.
-осінен бастап есептегенде) бөлетін сызықтың теңдеуін табыңыз.
Шешуі.
Айталық
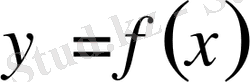 ізделінді функция,
ізделінді функция,
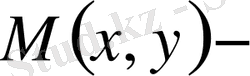 қисықтың кез келген нүктесі,
қисықтың кез келген нүктесі,
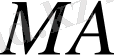 қисыққа жанама.
қисыққа жанама.
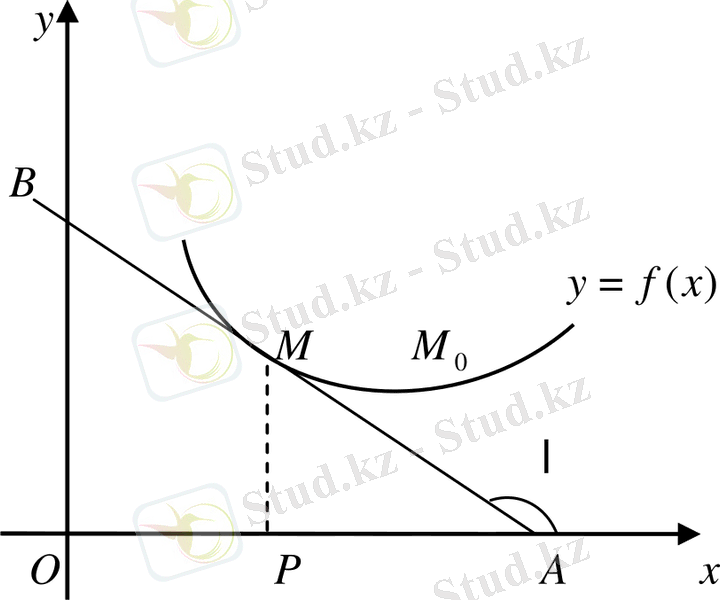
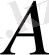 - жанаманың
- жанаманың
 осімен,
осімен,
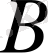 - оның
- оның
 осімен қиылысу нүктелері,
осімен қиылысу нүктелері,
 нүктесінің
нүктесінің
 осіндегі проекциясы болсын (7-сурет) . Жанаманың
осіндегі проекциясы болсын (7-сурет) . Жанаманың
 осінің
осінің
оң бағытымен жасайтын бұрышын
 деп белгілейік, онда
деп белгілейік, онда
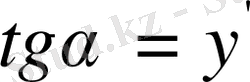 .
.
Екінші жағынан 7-сурет бойынша:
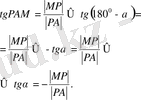
7-сурет
Алынған қатынасты
 нүктесінің ағымдық координаттары арқылы өрнектейік.
нүктесінің ағымдық координаттары арқылы өрнектейік.
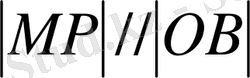 болғандықтан
болғандықтан
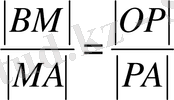 болады.
болады.
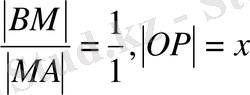
екендігін ескерсек,
 және
және
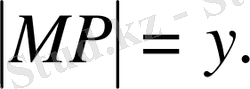 Демек,
Демек,
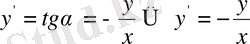 .
.
Бұл алынған теңдеу айнымалылары ажыралатын бірінші ретті дифференциалдық теңдеу.
Айнымалыларды ажыратып интегралдасақ:
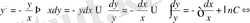
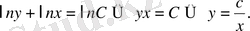
Бұл
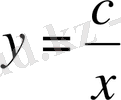 интегралдық қисықтар үйірінен
интегралдық қисықтар үйірінен
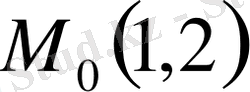 нүутесі арқылы өтетін қисықты таңдап аламыз.
нүутесі арқылы өтетін қисықты таңдап аламыз.
Ол үшін
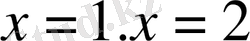 мәндерін теңдеудің жалпы шешіміне қойсақ:
мәндерін теңдеудің жалпы шешіміне қойсақ:
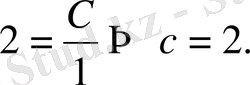
Демек ізделінген қисық теңдеуі
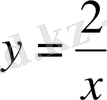 болады.
болады.
3 § Бір текті дифференциалдық теңдеулер.
Айталық
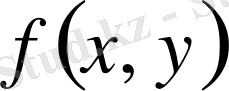 функциясы берімін. Егер кез келген
функциясы берімін. Егер кез келген
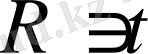 нақты саны үшін
нақты саны үшін
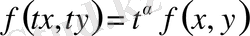 (4)
(4)
теңдігі орындалатын болса, онда
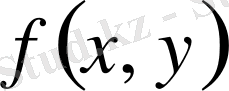 функциясы
функциясы
 шы ретті біртекті функция
деп аталады.
шы ретті біртекті функция
деп аталады.
Мысалы:
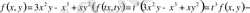 үшінші ретті біртекті функция;
үшінші ретті біртекті функция;
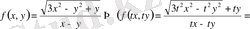
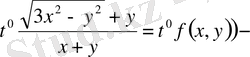 нөлінші ретті біртекті функция.
нөлінші ретті біртекті функция.
Егер
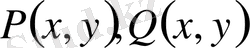 - бірдей ретті біртекті функциялар болса, онда
- бірдей ретті біртекті функциялар болса, онда
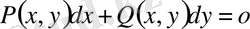 (5)
(5)
біртекті функционалдық теңдеу деп аталады.
Дербес жағдайда,
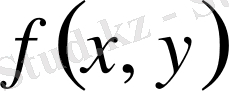 - нөлінші ретті біртекті функция болса, онда
- нөлінші ретті біртекті функция болса, онда
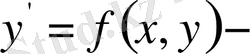 біртекті дифференциалдық теңдеу.
біртекті дифференциалдық теңдеу.
Енді біртекті дифференциалдық теңдеуді интегралдау жолдарын көрсетейік. Ол үшін (5) теңдеудің екі жағын да
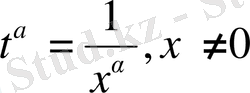 шамасына көбейту арқылы,
шамасына көбейту арқылы,
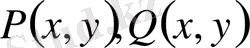 функцияларын түрлендіреміз.
функцияларын түрлендіреміз.
Сонымен,
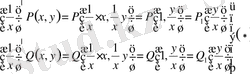
Егерде
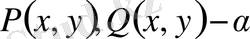 ретті біртекті функциялар болса, онда (5) теңдеудің екі жағын да
ретті біртекті функциялар болса, онда (5) теңдеудің екі жағын да
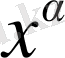 шамасына бөлу арқылы,
шамасына бөлу арқылы,
 теңдіктерді ескере отырып,
теңдіктерді ескере отырып,
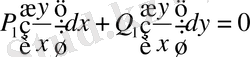 (6)
(6)
теңдеуін аламыз. Осы алынған теңдікке
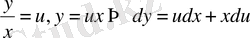 (7)
(7)
ауыстыруын қолдансақ, түрлендірілген (6) теңдеу айнымалылары ажыратылатын теңдеуге айналады. Шынында да, (6) теңдеуге (7) ауыстыруды қолдансақ,
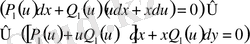
айнымалылары ажыратылатын теңдеу. Ал оны шешу алдыңғы параграфта келтірілген.
14- Мысал
.
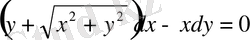 теңдеуін интегралдайық.
теңдеуін интегралдайық.
Шешуі.
Берілген теңдеудегі
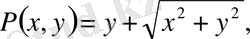
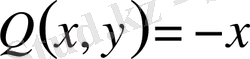 функцияларын біртектілікке тексерейік:
функцияларын біртектілікке тексерейік:
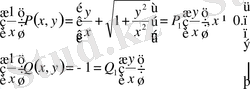
Демек,
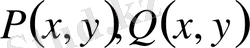 бірінші ретті біртекті функциялар. Ал берілген теңдеу біртекті дифференциалдық теңдеу, яғни
бірінші ретті біртекті функциялар. Ал берілген теңдеу біртекті дифференциалдық теңдеу, яғни
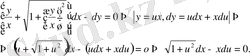
Бұл теңдеу айнымалылары ажыратылатын теңдеу.
Ендеше,
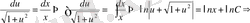
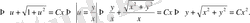
Берілген теңдеудің жалпы интегралын алдық. Бұған қоса
 шамасы да берілген теңдеудің шешімі болатындығына оңай көз жеткізуге болады.
шамасы да берілген теңдеудің шешімі болатындығына оңай көз жеткізуге болады.
Ескерту.
Кей кездері біртекті теңдеулерді
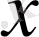 айнымалысын
айнымалысын
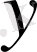 -тің функциясы, яғни
-тің функциясы, яғни
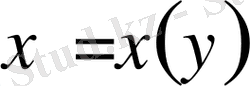 түрінде интегралдау ыңғайлы болады. Бұл кезде
түрінде интегралдау ыңғайлы болады. Бұл кезде
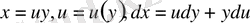 ауыстыруын енгіземіз.
ауыстыруын енгіземіз.
Енді біртекті дифференциалдық теңдеуге келтірілетін
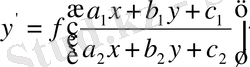 (8)
(8)
түріндегі теңдеуді қарастырайық.
Ол үшін ескі
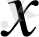 және
және
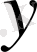 айнымалыларының орнына жаңадан
айнымалыларының орнына жаңадан
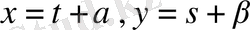 (9)
(9)
теңдіктері арқылы
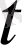 және
және
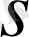 айнымалыларын енгіземіз. Мұндағы
айнымалыларын енгіземіз. Мұндағы
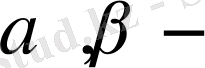 кейбір сандар.
кейбір сандар.
Бұл кезде
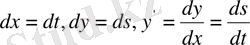 болады да, берілген (8) теңдеу
болады да, берілген (8) теңдеу
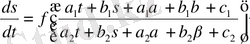 түрін қабылдайды. Мұндағы
түрін қабылдайды. Мұндағы
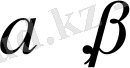 сандарын соңғы теңдеу біртекті теңдеуге айналатындай етіп таңдауымыз керек. Ол үшін, ол теңдеудің белгілі бір бөлігін, яғни
сандарын соңғы теңдеу біртекті теңдеуге айналатындай етіп таңдауымыз керек. Ол үшін, ол теңдеудің белгілі бір бөлігін, яғни
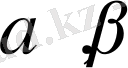 сандары:
сандары:
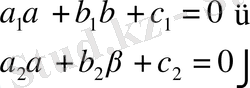 (10)
(10)
теңдеулер жүйесін қанағаттандыратындай етіп аламыз.
Егер негізгі анықтауыш
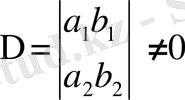 болса, онда (10) теңдеулер жүйесінің жалғыз ғана шешімі болатын
болса, онда (10) теңдеулер жүйесінің жалғыз ғана шешімі болатын
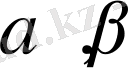 сандары табылып, берілген (8) теңдеу жаңа
сандары табылып, берілген (8) теңдеу жаңа
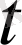 және
және
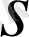 айнымалылары арқылы біртекті дифференциалдық теңдеуге айналады:
айнымалылары арқылы біртекті дифференциалдық теңдеуге айналады:
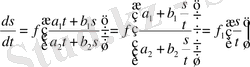

Ендеше,
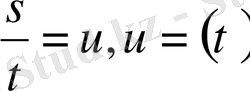 ауыстыруын жасау арқылы
ауыстыруын жасау арқылы
 теңдеуді айнымалылары ажыратылатын теңдеуге келтіреміз. Оны шешу жолдары жоғарыда келтірілген.
теңдеуді айнымалылары ажыратылатын теңдеуге келтіреміз. Оны шешу жолдары жоғарыда келтірілген.
Егер
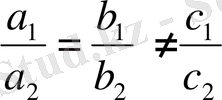 қатынастары орындалатын болса, онда
қатынастары орындалатын болса, онда
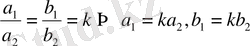 белгілеулеріне енгізу арқылы, (8) теңдеу
белгілеулеріне енгізу арқылы, (8) теңдеу
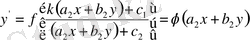
түріне келтіріледі. Соңғы теңдеуге
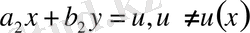 ауыстыруын енгізіп, (8) теңдеуді айнымалылары ажыратылатын теңдеуге келтіреміз.
ауыстыруын енгізіп, (8) теңдеуді айнымалылары ажыратылатын теңдеуге келтіреміз.
Ал
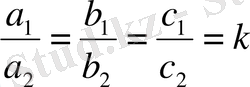 қатынастары орындалатын болса, онда берілген (8) теңдеудің оң жағы тұрақтыға айналып
қатынастары орындалатын болса, онда берілген (8) теңдеудің оң жағы тұрақтыға айналып
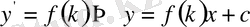 түрін қабылдайды.
түрін қабылдайды.
15-мысал.
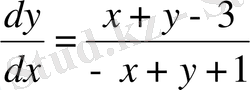 дифференциалдық теңдеуін шешейік (интегралдайық) .
дифференциалдық теңдеуін шешейік (интегралдайық) .
Шешуі.
Ол үшін (9) ауыстыруын енгіземіз, яғни
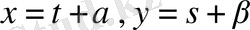 . Онда берілген теңдеу
. Онда берілген теңдеу
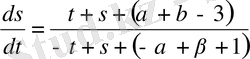 түрін қабылдайды. Ендеше
түрін қабылдайды. Ендеше
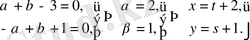
Демек,
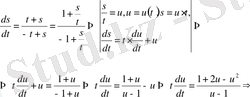
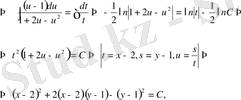
Берілген дифференциалдық теңдеудің жалпы интегралын алдық.
16- мәселе. Жанама асты жанасу нүктесінің абсциссасы және ординатасының қосындысына тең болған қисық сызықтарды табу керек.
Шешуі: Мәселе шарты бойынша
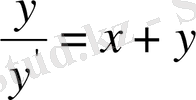
немесе дифференциалдарда жазсақ,
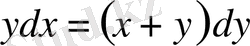
дифференциалдық теңдеуге ие боламыз.
Бұл теңдеуде
 ауыстыру емес, бәлкім
ауыстыру емес, бәлкім
 ауыстыруын енгізу тиімді. Ол жағдайда
ауыстыруын енгізу тиімді. Ол жағдайда
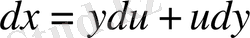 және теңдеу
және теңдеу
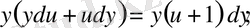

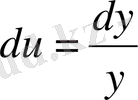 түріне келеді.
түріне келеді.
Бұл жерден
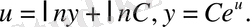 Жалпы шешім
Жалпы шешім
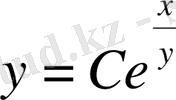 қисық сызықтар үйірі болады.
қисық сызықтар үйірі болады.
17-мәселе . Айналу осінің О нүктесіне жайғастырылған жарықтың көзінен шығатын барлық сәулелер рефлектор айнасынан бұл осіне паралел болып қайтуы үшін рефлектор айнасын қайсы айналу беті бойынша тегістеу керек. (8-сурет) .
Шешуі.
Ізделінді айналу бетінің меридиан бөлігін аламыз. Координаталар кіндігін О нүктеде деп аламыз,
 осін айналу осі бойынша бағыттаймыз. Егер
осін айналу осі бойынша бағыттаймыз. Егер
 оспен қисық сызықтың
оспен қисық сызықтың
 нүктесіне өткізілген
нүктесіне өткізілген
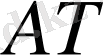 жанама арасындағы бұрышты
жанама арасындағы бұрышты
 арқылы белгілесек, ол жағдайда мәселе шарты бойынша:
арқылы белгілесек, ол жағдайда мәселе шарты бойынша:
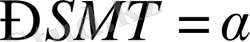
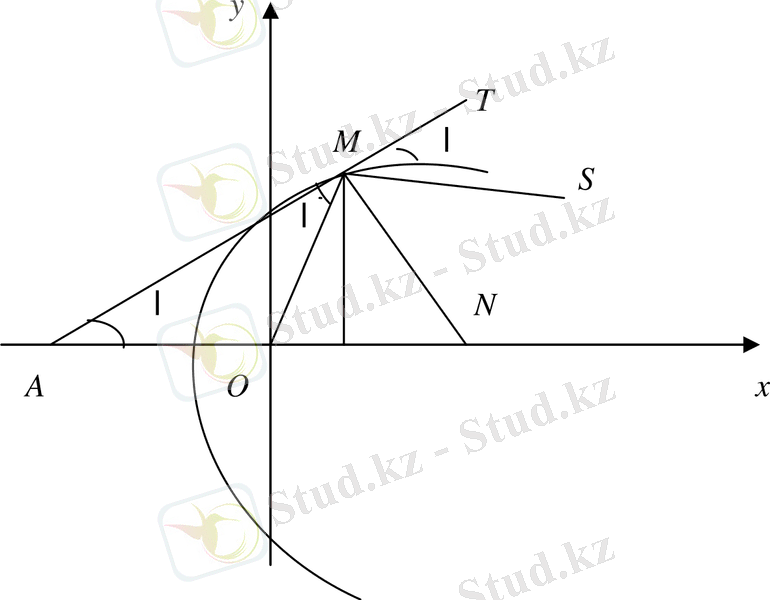
8- сурет
Екінші жағынан, бұрыштар түсу бұрышы
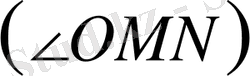 және қайту бұрышы
және қайту бұрышы
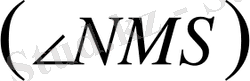
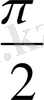 ге толықтырушы бұрыштар болғандықтан
ге толықтырушы бұрыштар болғандықтан
 және бұдан
және бұдан
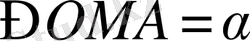 . Сондықтан,
. Сондықтан,
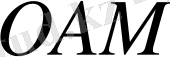 үшбұрышы тең бүйірлі және
үшбұрышы тең бүйірлі және
 Сызбадан:
Сызбадан:
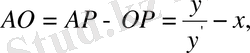
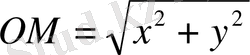 , нәтижеде
, нәтижеде
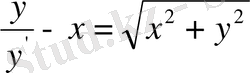
дифференциалдық теңдеуді құраймыз немесе дифференциалдарда жазсақ,
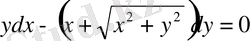 .
.
Бұл
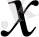 және
және
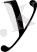 ке салыстырғанда біртекті теңдеу
ке салыстырғанда біртекті теңдеу
 және сәйкес ретте
және сәйкес ретте
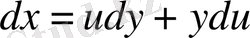 орнына қою жәрдемінде бұл теңдеуді айнымалылары ажыратылатын теңдеуге келтіреміз:
орнына қою жәрдемінде бұл теңдеуді айнымалылары ажыратылатын теңдеуге келтіреміз:
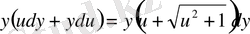
немесе
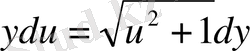
бұдан
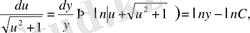
яғни
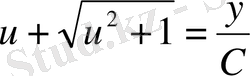 .
.
Иррационалдықтан құтқарып, бұл теңдеуді ықшайдаймыз:
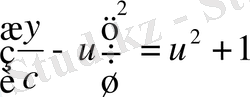
немесе
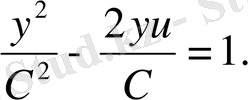
Ескі
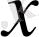 айнымалысына қайтып, жалпы интегралды табамыз:
айнымалысына қайтып, жалпы интегралды табамыз:
(7)
бұл симметрия өсі
 оспен бетпе -бет түсетін, яғни беттесетін, параметр
оспен бетпе -бет түсетін, яғни беттесетін, параметр
 болған және төбесі координаталар басынан сол жақта
болған және төбесі координаталар басынан сол жақта
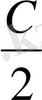 арақашықтықта жататын параболалар үйірі (әулеті) . Демек, айналу беттері айналу параболоидтары болып, олардың
арақашықтықта жататын параболалар үйірі (әулеті) . Демек, айналу беттері айналу параболоидтары болып, олардың
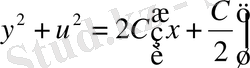
теңдеулері белгілі заң ереже бойынша
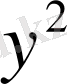 ты
ты
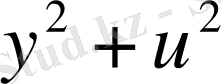 арқылы алмастыру бойынша құралған.
арқылы алмастыру бойынша құралған.
Егер айнаның диаметрі
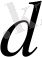 және тереңдігі
және тереңдігі
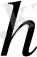 берілген болса, парабола теңдеуінен
берілген болса, парабола теңдеуінен
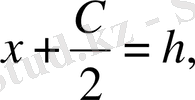
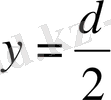 деп, С - ның мәнін анықтау мүмкін:
деп, С - ның мәнін анықтау мүмкін:
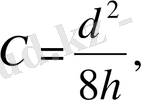 ол жағдайда парабола теңдеуі
ол жағдайда парабола теңдеуі
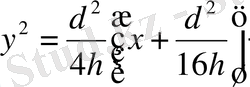 (дербес интеграл), айналу параболондының теңдеуі
(дербес интеграл), айналу параболондының теңдеуі
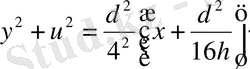 болады.
болады.
 18-мәселе
.
18-мәселе
.
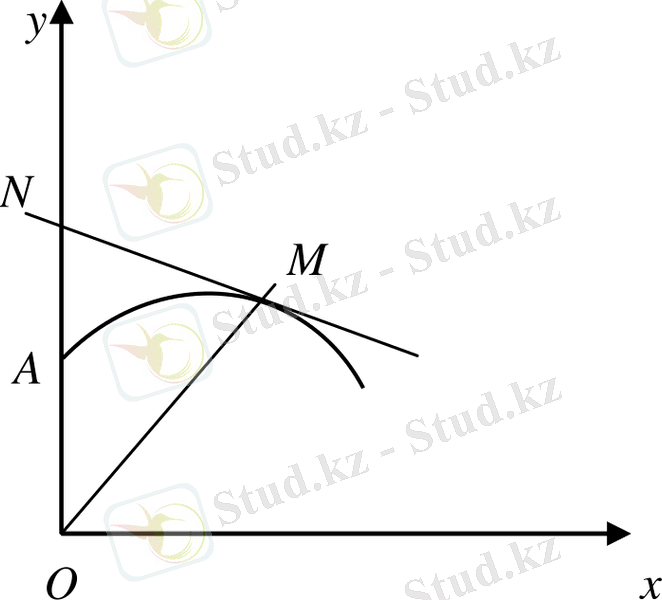
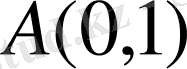 нүктесін өтетін
нүктесін өтетін
 өсімен және жанасу нүктесінен радиус-вектормен тең бүйірлі үш бұрыш жасайтын қисық
өсімен және жанасу нүктесінен радиус-вектормен тең бүйірлі үш бұрыш жасайтын қисық
сызықты табу керек. (9- сурет)
Шешуі.
Айталық,
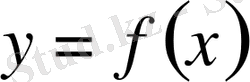 -
-
ізделінді қисық сызық теңдеуі болсын.
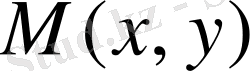 кез келген нүктеден қисыққа
кез келген нүктеден қисыққа

жанама өткізсек, бұл жаңа
 өсін
өсін

нүктеде қияды. Берілген шарт 9- сурет
бойынша
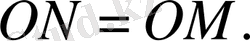 Бірақ
Бірақ
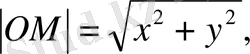 ал
ал
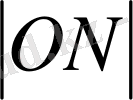 ді жанама теңдеуінен яғни
ді жанама теңдеуінен яғни
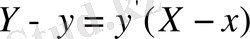

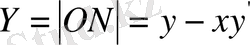
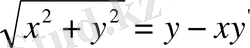
бір текті теңдеуге ие боламыз.
 алмастыруынан және ажыратылатын теңдеуге келтіріп табамыз:
алмастыруынан және ажыратылатын теңдеуге келтіріп табамыз:
немесе
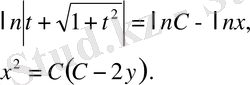
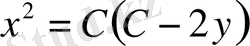 параболалар әулетіне ие боламыз.
параболалар әулетіне ие боламыз.
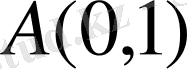 нүктенің координаттарын қойып
нүктенің координаттарын қойып
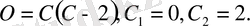
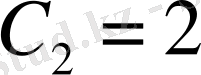 шешім жарайды, өйткені
шешім жарайды, өйткені
 болғанда парабола
болғанда парабола
 өсіне айналады. Ізделінді қисық парабола болып оның теңдеуі
өсіне айналады. Ізделінді қисық парабола болып оның теңдеуі
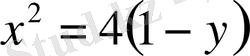 немесе
немесе
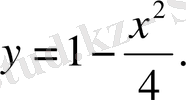
4 § Сызықтық теңдеулер
Ізделінді
 функциясы және оның туындысы арқылы сызықты болатын,
функциясы және оның туындысы арқылы сызықты болатын,
(9)
теңдеуі бірінші ретті сызықты дифференциалдық теңдеу деп аталады. Мұндағы
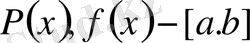 кесіндісінде үзіліссіз функциялар. Егер
кесіндісінде үзіліссіз функциялар. Егер
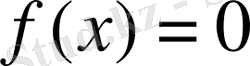 болса
болса
(10)
бір текті сызықты дифференциалдық теңдеу, ол
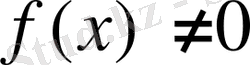 болса, біртекті емес дифференциалдық теңдеу деп аталады.
болса, біртекті емес дифференциалдық теңдеу деп аталады.
Теорема.
Егер
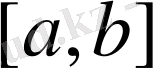 кесіндісінде
кесіндісінде
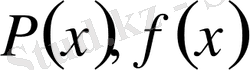 үзіліссіз болса, онда осы кесіндіде (9) теңдеудің
үзіліссіз болса, онда осы кесіндіде (9) теңдеудің
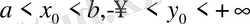 үшін,
үшін,
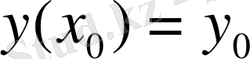 - бастапқы шартты қанағаттандыратын жалгғыз ғана шешімі болады.
- бастапқы шартты қанағаттандыратын жалгғыз ғана шешімі болады.
Бұл теореманың дәлелдеуін келтірместен бұрын, бірінші ретті (9) сызықты дифференциалдық теңдеуді интегралдаудың тәсілдерінің кейбіреулеріне тоқталайық.
1
 Айнымалыларды алмастыру (Бернулли) тәсілі.
Айнымалыларды алмастыру (Бернулли) тәсілі.
Бұл тәсіл бойынша (9) теңдеудің шешімін
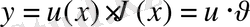 (11)
(11)
түрінде іздейміз. Мұндағы
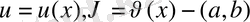 интервалында үзіліссіз дифференциалданатын функциялар. Онда (10) теңдіктің туындысы
интервалында үзіліссіз дифференциалданатын функциялар. Онда (10) теңдіктің туындысы
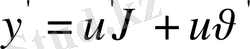 болады да, (9) теңдеу
болады да, (9) теңдеу
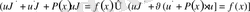 (12)
(12)
түрін қабылдайды.
Демек,
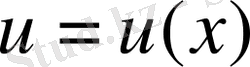 функциясы үшін (10) біртекті диффеенциалдық теңдеудің жалпы шешімін алуға болады. Ендеше (12) теңдіктегі квадрат жақша ішіндегі
функциясы үшін (10) біртекті диффеенциалдық теңдеудің жалпы шешімін алуға болады. Ендеше (12) теңдіктегі квадрат жақша ішіндегі
(13)
айнымалылары ажыратылатын теңдеу. Сондықтан,

(14)
Мұндағы
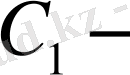 интегралдық тұрақты. Енді (13) және (14) теңдіктерді ескере отырып, (12) дифференциалдық теңдеуді шешеміз:
интегралдық тұрақты. Енді (13) және (14) теңдіктерді ескере отырып, (12) дифференциалдық теңдеуді шешеміз:
 (15)
(15)
Мұндағы
 тағы да интегралдық тұрақты. Сонымен, (15) және (14) теңдіктерді (11) теңдігіне қою арқылы, берілген (9) бірінші ретті сызықты дифференциалдық теңдеудің жалпы шешімін (интегралын) аламыз.
тағы да интегралдық тұрақты. Сонымен, (15) және (14) теңдіктерді (11) теңдігіне қою арқылы, берілген (9) бірінші ретті сызықты дифференциалдық теңдеудің жалпы шешімін (интегралын) аламыз.
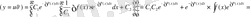
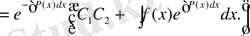
Ал
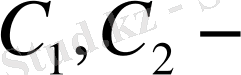 көбейтіндісі тұрақты кейбір сан болғандықтан оны бір тұрақтымен алмастыруға болады. Ендеше, іздестіріліп отырған шешім
көбейтіндісі тұрақты кейбір сан болғандықтан оны бір тұрақтымен алмастыруға болады. Ендеше, іздестіріліп отырған шешім
(16)
өрнегімен анықталады.
19-мысал
теңдеуін шешейік.
Шешуі.
Келтірілген тәсіл бойынша
 ,
,
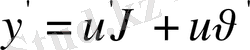 болғандықтан, берілген теңдеу
болғандықтан, берілген теңдеу
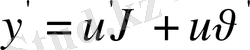
түріне көшеді. Онда (12) - (16) өрнектерді қолдану арқылы
онда (11) бойынша
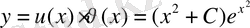 берілген теңдеудің жалпы шешімін (интегралын) аламыз.
берілген теңдеудің жалпы шешімін (интегралын) аламыз.
2
 Ерікті тұрақтыны вариациялау (Лагранж) тәсілі.
Ерікті тұрақтыны вариациялау (Лагранж) тәсілі.
Бұл тәсі бойынша алдымен (9) теңдеуді, айнымалалары ажыратылатын біртекті теңдеуді шешуден бастаймыз:
(17)
Мұндағы
 -
ерікті интегралдық тұрақты. Енді тұрақтыны вариациялау тәсілі бойынша берілген біртекті емес (9) сызықты дифференциалдық теңдеудің жалпы шешімін, (17) теңдіктегі
-
ерікті интегралдық тұрақты. Енді тұрақтыны вариациялау тәсілі бойынша берілген біртекті емес (9) сызықты дифференциалдық теңдеудің жалпы шешімін, (17) теңдіктегі
 -
ерікті тұрақтыны
-
ерікті тұрақтыны
 дифференциалданатын функция ретінде қарастырып қоямыз:
дифференциалданатын функция ретінде қарастырып қоямыз:
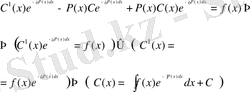
(18)
Енді (18) -
 мәнін (17) теңдікке қою арқылы
мәнін (17) теңдікке қою арқылы
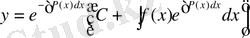 (19)
(19)
Жоғарыдағы алынған (19) -берілген (9) теңдеудің жалпы шешімін аламыз.
20-мысал.
дифференциалдық теңдеудің
бастапқы
шарты қанағаттандыратын шешімін табайық.
Шешуі. Алдымен
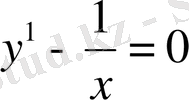
біртекті теңдеуді шешеміз:
Енді соңғы тәсіл бойынша,
 дифференциалданатын функция ретінде қарастырып,
дифференциалданатын функция ретінде қарастырып,
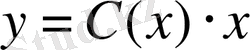 және
және
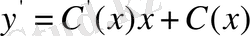 өрнектерін берілген дифференциалдық теңдеуге қою арқылы:
өрнектерін берілген дифференциалдық теңдеуге қою арқылы:
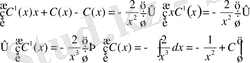

Табылған
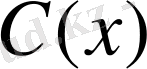 өрнегін
өрнегін
 теңдігіне қою арқылы,
теңдігіне қою арқылы,
берілген теңдеудің жалпы шешімін аламыз.
Келесі қадам
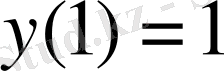 бастапқы шартты қолдану арқылы ерікті тұрақтыны анықтаймыз
бастапқы шартты қолдану арқылы ерікті тұрақтыны анықтаймыз
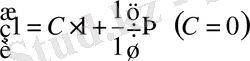 . Демек, берілген теңдеудің, берілген бастапқы шартты қанағаттандыратын шешімі
. Демек, берілген теңдеудің, берілген бастапқы шартты қанағаттандыратын шешімі
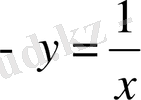 болып шығады.
болып шығады.
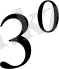 Демеушілік көбейткіш тәсілі.
Демеушілік көбейткіш тәсілі.
Сызықты бір текті емес (9) дифференциалдық теңдеуге арналған
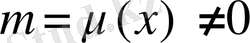 функциясын қарастырайық. Берілген (9) теңдеудің екі жағында оған көбейткенде
функциясын қарастырайық. Берілген (9) теңдеудің екі жағында оған көбейткенде
еңдігінің сол жағындағы өрнек, көбейтінді
 функциясының туындысы болатындай, яғни
функциясының туындысы болатындай, яғни
теңдігі орындалатындай
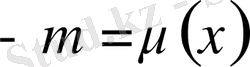 функциясын іздейміз. Осы теңдіктен,
функциясын іздейміз. Осы теңдіктен,
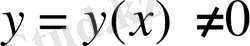 болғандықтан,
болғандықтан,
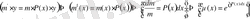 (20)
(20)
функциясын аламыз.
Демек, іздеп отырған
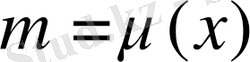 функциясы табылды. Ендеше,
функциясы табылды. Ендеше,
 және
және
 теңдіктерін пайдаланып, (19?) -ке сәйкес.
теңдіктерін пайдаланып, (19?) -ке сәйкес.
 берілген (9?) теңдеудің жалпы - «үйреншікті» шешімін аламыз.
берілген (9?) теңдеудің жалпы - «үйреншікті» шешімін аламыз.
Ал табылған
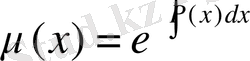 функциясы сызықты дифференциалдық теңдеуге теңдеуге арналған
демеушілік көбейткіш
деп аталады.
функциясы сызықты дифференциалдық теңдеуге теңдеуге арналған
демеушілік көбейткіш
деп аталады.
21-мысал . Демеушілік көбейткіш тәсілімен
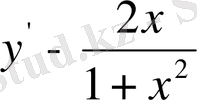
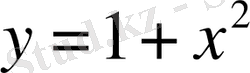
дифференциалдық теңдеуінің
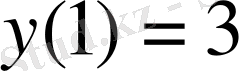 бастапқы шартты қанағаттандыратындай дербес шешімін табайық.
бастапқы шартты қанағаттандыратындай дербес шешімін табайық.
Шешуі.
Берілген теңдеуде
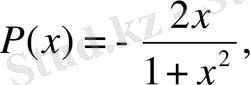
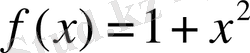 болғандықтан, демеушілік көбейткіш
болғандықтан, демеушілік көбейткіш
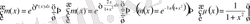 болады.
болады.
Ендеше, берілген екі теңдіктің екі жағында осы функцияға көбейтеміз,
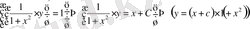
Енді берілген бастапқы шартты пайдаланамыз.
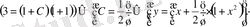
Берілген Коши есебінің шешімін аламыз.
Ескерту
.
Кей кездері берілген теңдеу
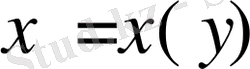 функциясына байланысты сызықты дифференциалдық теңдеу, яғни
функциясына байланысты сызықты дифференциалдық теңдеу, яғни
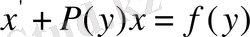 (21)
(21)
түрін қабылдайды. Бұл кезде, теңдеудің шешімін Бернулли тәсілі бойынша
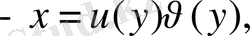 ол демеушілік көбейткіш
ол демеушілік көбейткіш
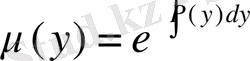 түрін ізделінеді.
түрін ізделінеді.
22-мысал .
теңдеуін шешейік.
Шешуі. Берілген теңдеуді түрлендірейік,
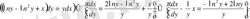
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz