Жай итерация әдісімен сызықсыз теңдеулерді шешуге арналған Turbo Pascal бағдарламасын құру және қателікті бағалау


Қ. А. Яссауи атындағы кәсіби колледжі
Курстық жоба
Тақырыбы: Жай итерация әдісі бойынша теңдеуді шешу бағдарламасын құру.
Орындаған: Токсанова Ш.
ТБ-11-08 тобы
Қабылдаған: Баялы А. Т
Түркістан-2009 ж.
Мазмұны
Кіріспе
1. Бөлім. Бір айнымалы бар сызықсыз теңдеулерді шешу . . .
1. 1. Есептің қойылуы . . . .
ІІ-бөлім Жай итерация әдісі . . .
2. 1 Итерация әдісі қателігін бағалау . . .
2. 2. Теңдеуді итерациялық түрге келтіру . . .
Қорытынды
Қосымша
Пайдаланылған әдебиеттер тізімі
Кіріспе
Тәжірбиелік есептеуде бағалануы қолайсыз бірақ қателік басты мүшесінің құрылымын құруда пайдасы. Мұнда мен жай итерация әдісін “Turbo Pascal 7. 0” жобалау ортасының программалау ортасына салып, есептеудің тиімді жолын айтуға болады.
Бір айнымалы бар сызықсыз теңдеулерді шешу көптеген және түрлі физикалық, механикалық, техниканың және басқа салалардағы қолданбалы анализдің маңызды есептерінің бірі болып табылады
Курстық жобаның мақсаты: жай итерация әдісі туралы түсінік, ерекшеліктері, жазу тәсілдері, блок -схемалар, программасы, орындаушының формуланы қолдану тәсілдері. жай итерация әдісін тиімді жолдарын көрсету.
Зерттеу міндеттері: жай итерация әдісінің сандық әдістермен жуықтап есептеудің тиімділігі.
Зерттеу объектісі: жай итерация әдісін қолданып, теңдеулерді есептеу жолдарын зерттеу.
Зерттеу пәні: Өндірістік және экономикалық процестерді модельдеу.
Зерттеу әдістері: Ғылыми оқу құралдары, оқулықтар, журналдар, жаңа ақпараттық технологиялар, Internet - сайттары.
Курстық жобаның көрнекілігі: Слайдтар, компьютер, проектор. схемалар.
Курстық жобаның құрылымы: Кіріспеден, екі бөлімнен, қорытындыдан, қосымша және пайдаланылған әдебиеттер тізімінен тұрады.
1. Бөлім. Бір айнымалы бар сызықсыз теңдеулерді шешу
1. 1. Есептің қойылуы.
Бір айнымалы бар сызықсыз теңдеулерді шешу көптеген және түрлі физикалық, механикалық, техниканың және басқа салалардағы қолданбалы анализдің маңызды есептерінің бірі болып табылады.
Жалпы жағдайда сызықсыз теңдеуді
F(x) =0, (1. 1)
түрінде жазуға болады. Мұнда F(x) шекті және шексіз [a, b] интервалында анықтаған және үзіліссіз функция.
Кез келген
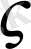
 [ a, b] саны F(x) функциясын нөльге айналдыратын, яғни F(
[ a, b] саны F(x) функциясын нөльге айналдыратын, яғни F(
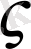 ) = 0, оны ( 1. 1) теңдеудің түбірі деп атайды.
) = 0, оны ( 1. 1) теңдеудің түбірі деп атайды.
Егер х =
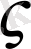 болғанда F(x) функциясымен оның (k - 1) дәрежеге дейінгі туындылары нөльге тең болса онда
болғанда F(x) функциясымен оның (k - 1) дәрежеге дейінгі туындылары нөльге тең болса онда
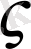 саны k еселі түбір деп аталады:
саны k еселі түбір деп аталады:
F(
 ) = F’(
) = F’(
 ) = …= F
( k-1)
(
) = …= F
( k-1)
(
 ) =0.
) =0.
Бір еселі түбір жай түбір деп аталады.
F(x) және G(x) біреуінің шешімі екіншісініңкі болса, яғни теңдеулер шешімдерінің жиындары сәйкес келсе, онда оларды тең дәрежелі (эквивалентті) деп атайды.
Бір бір белгісізі бар сызықсыз теңдеу алгебралық және трансценденттік болып бөлінеді.
Егер функция алгебралық болса (1. 1) теңдеу алгебралық деп аталады. Алгебралық түрлендірулер арқылы кез келген алгебралық теңдеуден канондық түрдегі теңдеу алуға болады:
P n (x) =a 0 x n + a 1 x n-1 + … + a n = 0.,
Мұнда а 0 , а 1 , . . . , а n - теңдеу коэффиценттері, х - белгісіз. n көрсеткіш алгебралық теңдеудің дәрежесі деп аталады.
Кез келген алгебралық теңдеудің кем дегенде бір нақты немесе комплексті түбірі болады.
Алгебралық теңдеу (1. 1) канондық түрге келтірілгенде оның түбірлері бастапқы теңдеудікіндей болады. Сонымен қатар кейбір артық түбірлер де пайда болуы мүмкін. Мысалы,
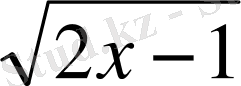 +х=
+х=
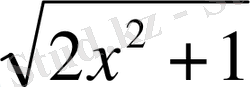 -1
-1
теңдеуі канондық түрге келтірілгенде
7x 4 + 12x 3 + 2x 2 -4x-5= 0
болады.
Егер F(x) функциясы алгебралық болмаса (1. 1) теңдеуді трансценденттік деп аталады. Трансцендеттік теңдеудің мысалдары:
x- 10 sin x = 0; 2 x -2 cos x = 0; lg ( x+5) = cos x.
Кейбір жағдайларда трансценденттік теңдеулердің шешімдерін алгебралық теңдеулер шешіміне келтіруге болады.
Көптеген жағдайларда сызықсыз теңдеулердің шешімдерін аналитикалық түрлендіру арқылы (дәл әдістер ) болмайтындықтан, практикада оларды сандық әдістермен шешеді. Мұндай теңдеуді шешу - оның түбірі барлығын, түбірлер санын анықтау, және түбірлер мәнін берілген дәлдікпен табу. Әдетте, (1. 1) теңдеудің нақты және комплексті түбірлерін табу екі кезеңнен тұрады: түбірлерді бөліп алу яғни бір түбірдің мәні орналасқан қарастырылған областың шағын маңын табу, және түбірлерді дәлдеу, яғни берілген дәлдікпен қандайда бір аймақтағы түбірді есептеу.
Біз, (1. 1) теңдеудің нақты түбірлерін анықтайтын сандық әдістерді қарастырамыз. Кең таралған (1. 1) теңдеуді шешудің әдістері : аралықты бөлу, айыру әдісінін нақты түбірлер табу әдісі, итерация әдісі. Осы әдістердің біреуін қолдану түбірлер санына, бастапқы жақындауға және F(x) функцияның жағдайына байланысты болады. ЭЕМ - де жиі қолданылатын аралықты бөлу әдісін қарастырамыз.
2. Бөлім. Жай итерация әдісі.
(1. 1) теңдеуін теңдәрежелі теңдеумен алмастырамыз:
x=f(x) . (1. 3)
 - (1. 3) теңдеуінің түбірі, х
0
- қандай да әдіспен алынған
- (1. 3) теңдеуінің түбірі, х
0
- қандай да әдіспен алынған
 нөлдік жуықтау болсын. (1. 3) теңдеуінің оң жағына х
0
санын қойып, қандайда х
1
= f(x
0
) санын аламыз, х
1
санымен осылай жасап х
2
= f(x
1
) аламыз т. с. с. Қадам сайын x
n
= f(x
n-1
) қатынасын қолданып х
n,
x
1
, …. ., x
n
, …., (1. 4) тізбегін алады. Ол тізбекті итерациялық тізбек деп атайды.
нөлдік жуықтау болсын. (1. 3) теңдеуінің оң жағына х
0
санын қойып, қандайда х
1
= f(x
0
) санын аламыз, х
1
санымен осылай жасап х
2
= f(x
1
) аламыз т. с. с. Қадам сайын x
n
= f(x
n-1
) қатынасын қолданып х
n,
x
1
, …. ., x
n
, …., (1. 4) тізбегін алады. Ол тізбекті итерациялық тізбек деп атайды.
Итерациялық тізбекті жасаудың қарапайым геометриялық интерпретациясы бар.
 y
y
(x 1 )
(x 2 )
0 х
0
х1 х
2
 х
х
7 - сур.
Жуықтаулар тізбегі жинақталған немесе шашыраған болуы мүмкін. 7 суретте шашыраған тізбек көрсетілген
Егер (1. 4) тізбек жинақталған болса, ал f үздіксіз болса онда (1. 4) тізбектің шегі (1. 3) теңдеудің шешімі болады.
Шынында
 =
=
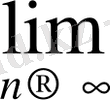 x
n
x
n
= f(x
n-1
) шегіне көшеміз:
x
n
x
n
= f(x
n-1
) шегіне көшеміз:
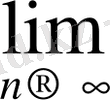 x
n
=
x
n
=
 f (x
n-1
) = f (
f (x
n-1
) = f (
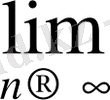 x
n-1
) = f (
x
n-1
) = f (
 ) (1. 5)
) (1. 5)
яғни
 = f (
= f (
 ) .
) .
7 - суретте көрініп тұрғандай итерация әдісі түбірді дәлелдеуге алып келмеуі де мүмкін. Итерациялық процестің жеткілікті жинақтылық шартын төмендегі теорема көрсетеді.
Терорема 1. 1. x= f (x) теңдеуінің [a, b] аралығында жалғыз түбірі бар болсын және төмендегі шарттар орындалсын:
- F(x) [a; b] аралығында анықталған және дифферциалданады.
- Барлық х[a; b] үшін х[a; b] ;
- Барлық x[a; b] үшін │f׳(x) │<= q < 1 болатындай нақты q саны болады.
Сонда х
n
= f(x
n-1
) (n=1, 2, …) итерациялық тізбегі кез келген бастапқы х
0
 │a; b│ үшін жинақталған болады.
│a; b│ үшін жинақталған болады.
Дәлелдеу (1. 4) итерациялық тізбекті кез келген бастапқы х
0
 │a; b│мәні үшін жасайық. (2) шартқа сәйкес тізбектің барлық мүшелері [a; b] кесіндісінде орналасқан.
│a; b│мәні үшін жасайық. (2) шартқа сәйкес тізбектің барлық мүшелері [a; b] кесіндісінде орналасқан.
Екі x
n =
f(x
n-1
) және x
n+1
= f(x
n
) екі жуықтар тізбегін қарастырайық. Лагранждың соңғы өсімшелер жөніндегі теоремасы бойынша x
n+1
- x
n
= f (x
n
) - f(x
n-1
) = f
׳
(c) (x
n
- x
n-1
), c
 [x
n-1
; x
n
] . Модульге өтіп және (3) шартын ескере отырып, алатынымыз: │x
n-1
- x
n
│=│f
׳
(c) │* │x
n
- x
n-1
│<= q│x
n
- x
n-1
│
׳
│x
n-1
- x
n
│< = q │x
n
- x
n-1
│.
[x
n-1
; x
n
] . Модульге өтіп және (3) шартын ескере отырып, алатынымыз: │x
n-1
- x
n
│=│f
׳
(c) │* │x
n
- x
n-1
│<= q│x
n
- x
n-1
│
׳
│x
n-1
- x
n
│< = q │x
n
- x
n-1
│.
n= 1, 2, … болғанда :
│x 2 -x 1 │<= q│x 1 -x 2 │ (1. 6)
│x 3 -x 2 │<=q 2 │x 1 - x 0 │,
│x n -1 - x n│<= q n │x 1 - x 0 │.
X 0 +( x 1 -x 2 ) +( x 2 - x 1 ) + …+( x n - x n -1 ) + …. ( 1. 7 )
Қатарын қарастырамыз.
Осы қатардың жеке қосындысын S 1 = x 0 , S 2 = x 1 , …. ., S n+1 = x n орындайық.
(1. 7) Қатардың ( n+1) - ші жеке қосындысы (1. 4) тізбектің n - ші итерациялық мүшесімен сәйкес келеді, яғни :
S n+1 = x n (1. 8)
(1. 7) қатарды
│x 1 - x 0 │+ q│x 1 - x 0 │+ q 2 │x 1 - x 0 │ ( 1. 9)
қатарымен салыстырамыз.
Байқағанымыз, (1. 6) қатынасқа байланысты (1. 7) қатардың абсольюттік шамасы ( х 0 мүшесі ескерілмейді ) ( 1. 9) қатардың сәйкес мүшелерінен үлкен болмайды. Бірақ ( 1. 9) қатар абсолютті кемімелі геометриялық прогрессия түрінде жинақталады. (шарт бойынша q<1) .
Сондықтан ( 1. 7) қатар жинақталады, яғни онық жеке қосындысы (1. 8) шегі болады.
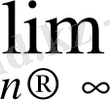 x
n
=
x
n
=
 болсын. F функциясының үздіксіздігінен
болсын. F функциясының үздіксіздігінен
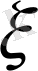 =f(
=f(
 ) екендігі алынады, яғни
) екендігі алынады, яғни
 - x = f(x) теңдеуінің шешімі.
- x = f(x) теңдеуінің шешімі.
2. 1 Итерация әдісі қателігін бағалау.
1. 1 Теоремадан оның шарттары орындалғанда итерациялық тізбек х 0 дің кез келген нөлге тең мәнінде жинақталады. Осыдан қажет болса итерациялық процесте n - ді жуықтауды бастапқы деп алуға болады. Ол есептеу кезінде қателіктер жіберілгенін, бірақ олар соңғы нәтижеге әсер етпейтіндігін көрсетеді.
Сонымен қатар практикада итерациялық тізбекті жасау шексіз ұзаққа созылмайды. Итерациялық тізбектің шегінің болуы, оның шын мәнін эмпириалдық жолмен алуға болады деген сөз емес. Белгілі қателікке жол беріп бұл процесті үзуге тура келеді. N- жуықтауда қателікті анықтауға мүмкіндік беретін формуланы анықтайтық.
X
n
- x= f(x) теңдеудің түбіріне жақын сан болсын.
 x
n
абсолют қателіке жуықтау төмендегі модульмен бағаланады:
x
n
абсолют қателіке жуықтау төмендегі модульмен бағаланады:
 x
n
= │
x
n
= │
 - x
n
│
- x
n
│
(1. 7) және (1. 8) - дерді ескеріп:
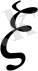 - x =
- x =
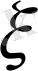 - S
n+1
= ( x
n+1
- x
n
) + ( x
n+2
- x
n+1
) + …. . (1. 10)
- S
n+1
= ( x
n+1
- x
n
) + ( x
n+2
- x
n+1
) + …. . (1. 10)
(1. 10) ды (1. 9) қатарының қалдығымен салыстырып:
q n │x 1 - x 0 │+q n+1 │x 1 -x 0 │+ …. . (1. 11)
(1. 6) бағалауды ескеріп, алатынымыз:
│
 - x
n
│= q
n
│x
1
- x
0
│+ …=
- x
n
│= q
n
│x
1
- x
0
│+ …=
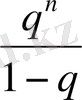 │x
1
-x
2
│.
│x
1
-x
2
│.
Сонымен қателіктің n- дік жуықтауын бағалауын формуласын аламыз:
 x
n
<= =
x
n
<= =
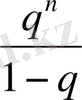 │x
1
-x
0
│. (1. 12) .
│x
1
-x
0
│. (1. 12) .
Практикада (1. 12) формуласының модификациясынын қолданады. Нөльдік мән үшін х
n-1
( x
0
орнына ) алынады. Келесі жуықтау x
n
(x
1
орнына) болады. Сонымен қатар 0<q<1 болғанда q
n
<= (n =1, 2, …) екенін ескеріп (1. 12) - ден :
 х
n
<=
х
n
<=
 │x
n
- x
n-1
│ (1. 13)
│x
n
- x
n-1
│ (1. 13)
алынады.
Бағалау (1. 12) және (1. 13) формулаларында 1. 1 теореманың (3) шарты бойынша орнатылған q нақты саны қолданылады. Барлық жағдайда q мәнін
│f(x) │тің x
 [a; b] - тегі туындысының жоғары мәні ретінде алуға болады. Байқалатыны, q - мәні үлкен болған сайын (1. 9) қатардың жинақталуы тез болады, сондықтан итерациялық қатар тезірек жинақталады.
[a; b] - тегі туындысының жоғары мәні ретінде алуға болады. Байқалатыны, q - мәні үлкен болған сайын (1. 9) қатардың жинақталуы тез болады, сондықтан итерациялық қатар тезірек жинақталады.
(1. 13) қатысты бағалағанда маңызды практикалық қорытынды шығады.
x = f(x) теңдеуі итерация әдісімен
 дәлдікпен шешілсін. Қай кезде есептеуді тоқтатуға болады.
дәлдікпен шешілсін. Қай кезде есептеуді тоқтатуға болады.
Ол шарт
 х
n
<=
х
n
<=
 болып табылады. (1. 13) бағалауды ескеріп алатынымыз:
болып табылады. (1. 13) бағалауды ескеріп алатынымыз:
 │x
n
- x
n-1
│<=
│x
n
- x
n-1
│<=
 ,
,
Осыдан
│x n - x n - 1 │<= (1- q) /q.
Осыдан x=f(x) теңдеуінің түбірін
 дәлдікпен итерация әдісімен анықтау үшін итерацияны екі көрші жуықтаулардың айырмасының модулі
дәлдікпен итерация әдісімен анықтау үшін итерацияны екі көрші жуықтаулардың айырмасының модулі
 (1-q) /q санына кіші болғанға дейін жалғастыру керек.
(1-q) /q санына кіші болғанға дейін жалғастыру керек.
2. 2. Теңдеуді итерациялық түрге келтіру.
F(x) =0 теңдеуі x= f(x) түріне көптеген әдістермен келтіруге болады, бірақ түрлендіруді 1. 1 теореманың (1) - (3) шарттары орындалатындай етіп орындау керек. Осы шарттардың ішінде ең қиындық келтіретіні (3) шарт болып табылады. Кейбір жағдайларда, кәдімгі түрлендірулермен қатар келесі әдістерді қолдану пайдалы болады:
а) f(x) =0 теңдеуі x = x - m * f (x) түрінде түрленеді, мұнда m - нөлден өзгеше константа. Осы жағдайда
f(x) = x - m*f(x) .
дифференциалдау арқылы алатынымыз:
f ' (x) = 1- mf ' (x) .
│f ' (x) │= │1-mf' (x) │<= q<1 болу үшін [a; b] кесіндісіндегі барлық х үшін m*f(x) <=1 болатындай етіп m таңдалады.
б) f(x) =0 теңдеуі x=f(x) түрінде жазылсын, бірақ [a; b] аралығында │f ' (x) │>1. Бұл жағдайда y= f(x) функциясы орнына f(x) - ке кері x = g(y) функциясын қарастырамыз. Енді y= g(y) (немесе ескі белгілеулерде x=g(x) ) теңдеуін шешеміз. Кері функциялардың тундысы қасиеті бойынша:
│g ' (x) │=
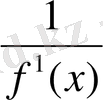 <1,
<1,
яғни 1. 1 теоремасының (3) шарты алдығы теңдеуге тең дәрежелі x= g(x) теңдеуі үшін орындалады.
Итерациялық әдіс бойынша қолмен есептеулер жасау үшін f(x) формуласының операциялық жазбалары бар кестесін пайдалануға болады ( 1. 1) . Оң бағанада жасалған есептеулер түбір табуда жуықтаулар үшін келесі бағанаға орналастырылады да есептеу жалғастырылады.
Таблица 1. 1
Номердің
жуықтауы x n . . . x n+1 =f (x n )
0 x 0 . . . x 1
1 x 1 . . . x 2 т. б. с
1. 6. 1 Мысал. Sin2х - ln x =0 теңдеуінің түбірін [1, 3; 1, 5] кесіндісінде итерациялық әдіспен 10 -4 дәлдікке дейін калькулятор көмегімен дәлдеу.
Бастапқы теңдеуді итерациялық түрге бірнеше әдістермен келтіруге болады, мысалы:
1) x = exp (sin2x) ;
2) x = (-1)
n
0, 5(arcsin ln x + n
 ), n = 1, 2…. ;
), n = 1, 2…. ;
3) x= x-n (sin2x - ln x), m ≠ 0.
Алынған нәтижелерге итерация әдісін қолдануды зерттейік.
1. Бірінші жағдайда f(x) = exp (sin2x) . F(x) функциясы [1, 3; 1, 5] кесіндісінде анықталған және дифференциалданады, бірақ 1. 1 теореманың екінші шарты орындалмайды: калькулятор көмегімен f(1, 3) = 1, 674478 болады, яғни кесіндінің сол жағында функция мәні кесіндінің сыртына шығып кетеді.
2. екінші жағдайда қарастырамыз. Бастапқы теңдеуге [1, 3; 1, 5] кесіндісінде тең дәрежелі теңдеу x= (π - arcsin lnx) /2 (1. 15)
алынады.
Мұнда f(x) = (π- arcsin lnx) /2. [1, 3; 1, 5] кесіндісінің барлық х мәндеріне f ' (x) =
 <0 екендігі байқалады, сондықтан f(x) функциясы берілген кесіндіде монотонды болады. Оның мәндерін [1, 3; 1, 5] кесіндінің ұштарында есептейміз.
<0 екендігі байқалады, сондықтан f(x) функциясы берілген кесіндіде монотонды болады. Оның мәндерін [1, 3; 1, 5] кесіндінің ұштарында есептейміз.
F(1, 3) = (π - arcsin lnx 1, 3) /2 = 1, 4380608,
F(1, 5) = (π - arcsin lnx 1, 5) /2 = 1, 3620528.
Алынған мәндер [1, 3; 1, 5] кесіндісіне енеді, ал f(x) функция монотонды, осыдан 1. 1 теореманың екінші шарты орындалатындығы байқалады.
Үшінші шартты тексеру үшін f(x) функциясы [1, 3; 1, 5] кесіндісінде туындысының модулін зерттейміз:
φ(х) = │f ' (x) │=
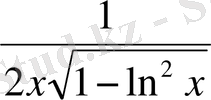 .
.
φ(х) функциясының туындысын табамыз:
φ' (x) =
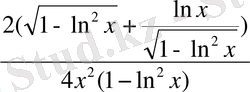 .
.
Жоғарыдағы туындыдан φ'(x) = [1, 3; 1, 5] кесіндісінің барлық бөлігінде теріс екендігін байқаймыз. Ол, φ(x) = │f ' (x) берілген кесіндіде кемитіндігін және максимумын сол жақ шетте жететінін : │f ' (1, 3) │=0, 3846153 көрсетеді.
Сонымен 1. 1 теоремасы (3) шарты орындалады. Егер q = 0, 39 болса. (1. 15) теңдеудің түбірлерін дәлдеу х 0 = 164 болғанда 1. 2 кестеде көрсетілген.
Кесте 1. 2
n x n x n+1 = -(arcsin lnx)
0 1, 4 1, 3992123
1 1, 3992123 1, 3995113
2 1, 3995113 1, 3993978
Мк - да есептеулер жасауға ыңғайлы болу үшін (π - arcsin ln x) /2 формуласын - (arcsin arcsin ln x - π) /2 түрінде жазады. Бұл есептеулерді аралық есептеулерді жазбай орындауға мүмкіндік береді.
Бағалау формуласы (1. 14) және бастапқы мәндер ε = 10 -4 және q= 0, 39 ескеріп үшінші жуықтауда алатынымыз:
x 3 - x 2 < 10 -4 (1-0, 39) /0, 39. Осыдан x 3 теңдеудің берілген шешімі болып табылады. Алынған нәтижені дөңгелектеп ең соңында алатынымыз
x = 1, 3994+ - 10 - 4 .
3. берілген теңдеудің үшінші көрсетілімін қалай қолдануға болатынын құрастырамыз:
x = x- m *(sin2x - ln x) .
Бұл жағдайда
f(x) = x - m(sin2x - ln x),
f ' (x) = 1- m (2 cos 2x -
 ) .
) .
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz