Жылуөткізгіштік теңдеуін нүктелік жылу көзін ескеріп шекті элементтер әдісімен шешу

МАЗМҰНЫ

КІРІСПЕ

Күнделікті өмірде қоршаған орташа үздіксіз жүріп жататын жылу алмасу құбылыстарын көптеп бақылауға болады. Олардың даму заңдылықтарын анықтау арқылы мұндай процестерді тиімді басқаруға, адам қажеттілігіне жаратуға болады. Аталған процестерге, мысалы, қысқы айларда ғимараттарды жылыту кезіндегі, немесе, әртүрлі жұмыстар атқаратын қондырғыларды суытуға байланысты орын алатын және тағы басқа процестер жатады.

Дипломдық жұмыста тұтас жазық денеде орын алатын стационарлық жылу алмасу процесін ішкі жылу көздерінің әсерін ескеріп зерттеу жоспарланған. Аталған процесс нәтижесінде денеде қалыптасатын температуралық өрістің деңгейіне әсер ететін сыртқы факторларды анықтау, олардың әсерін адамның қажеттігіне ыңғайлы деңгейде ұстап тұру мәселелерін шешу қазіргі таңда кезек күттірмейтін проблемаға айналып отыр. Қазақстан Республикасының егемендік еліміздің бас қаласы Астанада өтетін EXPO-2017 көрмесіне ұсынған “Болашақтың энергетикасы” тақырыбын таңдауы кездейсоқ емес. Бүгінгі таңда адамзат алдында тұрған ең маңызды мақсаттардың бірі - энергия көздерін ұтымды пайдаланып, олардың қоршаған ортаға келтіретін зиянын мейлінше азайту.

Математикалық физиканың көптеген есептерін тікелей аналитикалық жолмен шешу мүмкін емес екенін күнделікті өмір тәжірибесі көрсетіп отыр. Әсіресе зерттеу аймағының геометриясы күрделі болған кезде, немесе, зерттеу аймағы біртекті болмаған жағдайда және ол көпконтурлы болған кезде аналитикалық тәсілдер дәрменсіз болып қалады. Мұндай жағдайда вариациялық принциптердің біреуін қолданып арнайы функционал құру қажет, және сол функционалды минималдауды сандық әдістердің біреуімен орындаудан басқа жол жоқ. Жұмыста эллипс текті дербес туындылы дифференциалдық теңдеумен сипатталатын процеске мысал ретінде төртбұрышты жазық денедегі жылу таралу процесі қарастырылады. Жазық денедегі температуралық өрістің қалыптасуына қоршаған ортаның және ішкі жылу көздерінің әсері шекті элементтер әдісінің көмегімен жанжақты зерттеледі.

Зерттеу аймағындағы температуралық өріс жалпы жағдайда эллипс тектес дербес туындылы дифферециалдық теңдеумен сипатталады және оны шешу үшін математикалық физиканың аралас есебі қойылады. Арнайы құрылған функционалды минималдау шекті элементтер әдісімен орындалады. Есептің сандық нәтижесін алу үшін есептеу программасы MATLAB программалау жүйесінде құрылған және есептің шешімі графикалық әдіспен көрсетілген.

Жұмыстың идеясы:

• тұтас денелерде қалыптасатын температуралық өрісті зерттеудің теориялық негіздерін игеру;
• төрбұрышты жазық денедегі температуралық өрісті анықтау есебінің математикалық қойылымын негіздеу;
• зерттеу аймағында қалыптасатын температуралық өрістің деңгейіне қоршаған ортаның және ішкі жылу көздерінің әсерін шекті элементтер әдісімен зерттеу.

Зерттеулердің мақсаты: көпқабатты тұтас денедегі температуралық өрісті вариациялық приципті қолданып анықтаудың әдістемелік негізін жасау және денедегі температуралық өрістің қалыптасуына сыртқы орта мен ішкі жылу көздерінің әсерінің негізгі заңдылықтарын табу.

Қойылған мақсатқа сәйкес диссертациялық жұмыста келесі есептер шешіледі:

- тұтас денелерде қалыптасатын температуралық өрісті зерттеудің теориялық негіздері келтіріледі;

- төртбұрышты тұтас денедегі температуралық өрісті ішкі жылу көздерінің әсерін ескеріп анықтау есебінің математикалық қойылымы негізделеді;

- зерттеу аймағында қалыптасатын температуралық өрістің деңгейіне қоршаған орта мен ішкі жылу көздерінің әсері шекті элементтер әдісімен зерттеліп, нәтижесі графикалық түрде келтіріледі;

- алынған нәтижелерге талдау жасалынып, оларды қолдану жолдары көрсетіледі.

Төртбұрышты зерттеу аймағында қоршаған ортаның температурасы мен ішкі жылу көздерінің әсерінен қалыптасатын температуралық өрісті теориялық жолмен анықтау есебі көптеген инженерлік есептерде кеңінен қолданылып жүрген шекті элементтер әдісімен шешіледі. Есептің алгоритмын компьютерде жүзеге асыру үшін MATLAB жүйесінде құрылған есептеу программасы пайдаланылады.

Қорғауға шығарылған ғылыми тұжырымдар мен нәтижелер:

- есептеу аймағының сыртқы бетіндегі шекаралық шарттарды теориялық жолмен негіздеу әдістері;

- есептеу аймағының ішкі нүктелеріндегі жылу көздерінің әсерін теориялық жолмен ескеру әдістері;

- зерттеу аймағында қалыптасатын стационар температуралық өрістің сипаттамасы;

- қойылған есептің негізгі мақсаты орындалу үшін таңдалатын ішкі жылу көздерінің қуатын анықтау.

Диссертациялық жұмыс кіріспеден, үш бөлімнен тұратын негізгі мәтіннен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.

Бірінші бөлімде тұтас денеде үздіксіз жүріп жататын жылу алмасу процестерін зерттеудің тарихына қысқаша шолу жасалынған. Фурье мен Ньютон сипаттаған негізгі заңдылықтардан бастап жылуөткізгіштіктің дербес туындылы дифференциалдық теңдеулерін алуға дейінгі тарихи жол сарапталынған. Бөлімнің екінші жартысында эллипс текті дифференциалдық теңдеулерді вариациялық принциптерді қолданып шешудің жолдарына талдау жасалынған. Тұтас дененің ішкі аймағында орналасқан нүктелік жылу көздерінің температуралық өрістің қалыптасуына әсерін зерттеу алгоритмы келтірілген.

Екінші бөлімде диссертациялық жұмыста қарастырылатын жылуалмасу есебінің математикалық моделі құрылған. Ол үшін алдымен зерттеу аймағының шекаралары тағайындалып, шекаралық шарттар негізделген. Зерттеу аймағының ішкі бөлігінде орналасқан жылу көздерін орналастыру схемасы берілген. Бөлімнің соңында стационар температуралық өрісті сипаттайтын эллипс текті дифференциалдық теңдеуді шешудің аралас есебі қойылып, есепті шекті элементтер әдісімен шешудің негізгі алгоритмдері келтірілген.

Үшінші бөлім шекті элементтер әдісі негізінде жасалынған есептеу программасының жұмысының нәтижелерін талдауға арналған. Алдымен шекті элементтер негізінде жасалынған есептеу алгоритмы толығымен келтіріліп, есептің блок-схемасына түсініктеме берілген. Есептеу программасының жұмысының сандық нәтижелері MATLAB жүйесінде арнайы құрылған программалардың көмегімен температураның әрбір қималардағы графиктері түрінде берілген. Сонымен қатар сандық нәтижелерді айқын талдау үшін тұтас денеде қалыптасатын температуралық өрістің изотермалары келтірілген. Изотермаларды құру үшін жоғары деңгейлі DELPHI программалау жүйесінде арнайы «ИЗОЛИНИЙ» программасы жасалынған.

1 ШЕКТІ ЭЛЕМЕНТТЕР ӘДІСІН ТҰТАС ЖАЗЫҚ ДЕНЕДЕ

ҚАЛЫПТАСАТЫН ТЕМПЕРАТУРАЛЫҚ ӨРІСТІ ЗЕРТТЕУГЕ

ҚОЛДАНУ

1. СТАЦИОНАРЛЫҚ ЖЫЛУӨТКІЗГІШТІК ЕСЕБІНІҢ

ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

Теплофизика деп макроскопиялық жүйелердің термодинамикалық тепетеңдік күйлерін және осы тепетеңдік күйлердің бір біріне өту процестерін зерттейтін ғылымды айтады [1] .

Денелердің теплофизикалық қасиеттерін, денелердегі жылу энергиясының таралуын және әртүрлі денелер арасындағы жылу алмасу процестерін сипаттау үшін әртүрлі физикалық шамалар қолданылады. Мұндай шамалар шартты түрде бірнеше класқа бөлінеді.

Бірінші, ең маңызды класқа фундаменталдық физикалық шама - температура жатады. Температураның өлшем бірлігі Халықаралық СИ өлшемдер бірлігінің негізін құрайды.

Екінші класқа химиялық, физикалық және билогиялық процестерде бөлінетін жылу сияқты калориметриялық (өлшенетін) шамалар жатады. Мұндай шамаларға жану кезінде, сорбция, десорбция, фазалық өтулер, зат алмасу кезінде бөлінетін жылу мен жылусиғыштық та жатады.

Үшінші класты заттық орталардың жылу алмасу қасиеттерін сипаттайтын физикалық шамалар құрайды. Бұл класқа негізінен жылуөткізгіштік, жатады. Сонымен бірге бұл класқа жылуқабылдағыштық көрсеткіші және жылулық белсенділік сияқты кейбір туынды шамаларды да жатқызады.

Ал сәулелік жылу алмасуды сипаттайтын шамалар төртінші класты құрса, бесінші класты денелердің температураға байланысты өгеретін қасиеттерін сипаттайтын физикалық шамалар құрайды. Мысалы, соңғы класқа денелердің температуралық сызықтық созылу коэффициентін жатқызады [1] .

Келтірілген физикалық шамалардың ішінен ғылым мен техникадағы ең маңыздылары ретінде температура, жылу мөлшері, меншікті жылусиымдылық, жылуөткізгіштік және температуралық сызықтық созылу коэффициенті қабылданған.

Өлшем бірліктерін бір жүйеге келтіру үшін келтірілген физикалық шамалардың бірліктерінің мемлекеттік эталондары жасалынады [2] . Бұл эталондарда физикалық шамалардың өте үлкен дәлдікпен өлшенген мөлшерлері сақталады және оларды қажет кезінде сақталған жерлерінен алып отыруға болады.

Мысалы, Россия Федерациясында мемлекеттік эталондардың жартысы сақталатын ғылыми орталық Д. И. Менделеев атындағы Бүкілодақтық ғылыми зерттеу метрология институты (ВНИИМ) .

Халықаралық температуралық шкалаға (МТШ-90) сәйкес, негізгі физикалық шаманың, термодинамикалық температураның өлшемі ретінде К символымен белгіленетін кельвин қабылданған. Ол судың үштармақты нүктесінің термодинамикалық температурасының 1/273, 16 бөлігіне тең. Ал судың үштармақты нүктесінің термодинамикалық температурасы деп судың бу, сұйық және қатты күйлерінің өзара тепетеңдік жағдайда болатын кезінің температурасын айтады.

Күнделікті өмірде температура мұздың 273, 15 К болатын еру температурасы шамасымен салыстырылып өлшенеді. Осылайша алынған термодинамикалық температура Т символымен белгіленіп, Цельсий температурасы деп аталады, және ол

T/°C=T/K-273, 15

қатынасымен анықталады.

Цельсий температурасының өлшем бірлігі °C символымен белгіленіп, Цельсий градусы деп аталады. Ал температуралардың айырмашылығы кельвинмен немесе Цельсий градусымен өлшене береді, себебі температуралар айырымының абсолют шамасы өлшем бірлігін белгілеу тәсіліне тәуелді емес.

Жылуөткізгіштік деп тікелей жанасып тұрған денелердің энергиясы жоғары бөлшегінен энергиясы кем бөлшегіне қарай жылу энергиясының өту процесін сипаттайтын физикалық шаманы айтады.

Әртүрлі заттардың жылуөткізгіштігін алғаш рет 1789 жылы Ингенгуз зерттеді. Ал 1791 жылы граф Румфорд (Бенжамен Томсон) жылусақтағыш денелердің жылуөткізгіштігін салыстыруға арналған құрал жасап шықты. Жылуөткізгіштіктің толыққанды теориясын жасау 1822 жылы ұлы физик және математик Фурьенің ғана қолынан келді. Ол алғаш рет материалдардың жаңа қасиетінің - жылуөткізгіштігінің анықтамасын берді.

Жылу энергиясын техникада қолданудың күрт дамуына байланысты XX ғасырдың басында XVIII-XIX ғасырларда белгілі болған Био, Максвелл, Кельвин, Кольрауш сияқты атақты физик-зерттеушілердің орнына Гребер, Нуссельт, Якоб, Гриффитс сияқты жылу техникасын зерттеушілер келді.

Заттардың жылулық қасиеттерін өлшеу техникалық физиканың ең қиын есептерінің бірі болып есептеледі. Осыған байланысты XX ғасырдың жиырмасыншы жылдарынан бастап жылуөткізгіштікті өлшеумен Ұлыбритания, АҚШ, Франция сияқты дамыған елдердің мемлекеттік метрологиялық институттары айналыса бастады.

Россияда техникалық жылу өлшеу жұмыстары өткен ғасырдың отызыншы жылдары басталды. Осы кезеңде А. Ф. Иоффе мен М. В. Кирпичев басқарған физика-техникалық зертханада М. П. Стаценко жылусақтағыш материалдардың жылуөткізгіштігін өлшеуге арналған заманауи ғылымның деңгейіне сәйкес келетін құрал жасап шықты. Сонымен қатар, теплофизикалық өлшеулерді жүйелі түрде жүргізу үшін Г. М. Кондратьевтің [3, 4] басқаруымен арнайы ғылыми мектеп құрылып, бұл мектепте Г. Н. Дульнев, Б. Н. Олейник, О. А. Сергеев, Е. С. Платунов, Н. А. Ярышев және басқалар зерттеу жұмыстарын жүргізді. Осы кезеңде Г. М. Кондратьев Ленинградтың дәл механика мен оптика институтында жылулық өлшеулер кафедрасын ұйымдастырды. Жылуөткізгіштікті өлшеудің әдістерінің теориялық негіздері Г. Карслоу мен Д. Егердің, және А. В. Лыков пен А. Г. Шашковтың еңбектерінде қаланған [5-7] .

Жылуөткізгіштік құбылысы температураның gradT градиенті орын алған кезде пайда болады және бірөлшемді стационарлық жағдай кезінде Фурьенің

q = - λ· gradT

заңымен сипатталады. Бұл жерде q- жылу ағынының тығыздығы; λ - СИ жүйесінде жай ғана «жылуөткізгіштік» деп аталатын жылуөткізгіштік коэффициенті.

Жылуөткізгіштіктің дифференциалдық теңдеуін нақты шешу үшін бастапқы және шекаралық шарттар беріледі.

Жылуөткізгіштіктің өлшем бірлігі ретінде әрбір метр-кельвинге келетін Ватт [Вт/(м·К] алынған. Бұл шама сандық жағынан стационарлық режимде жылу ағынының беттің тығыздығы 1 Вт/м ² болған кезде температуралық градиентті 1 К/м шамасына жеткізетіндей заттың жылуөткізгіштігіне тең.

Жалпы жағдайда жылуөткізгіштік қысымның, зерттеліп отырған дененің құрамының, ылғалдылығының және оның температурасының функциясы.

Құрылыс материалдары мен жылусақтағыш материалдардың жылуөткізгіштігі әдетте 0, 02-3, 0 Вт/(м·К) шамасында болады. Температура көтерілген сайын ол өседі және оның шамасы заттың құрамына, қуыстық деңгейіне және ылғалдылығына байланысты өзгереді.

Әрбір нақты заттың жылуөткізгіштігін алдын ала дәл болжап айту теория жүзінде мүмкін емес. Сондықтан жылуөткізгіштікті дәл анықтау үшін тікелей өлшеуден басқа амал жоқ.

Жылусақтағыш заттардың жылуөткізгіштігін анықтауға осы заттың өзінен жасалған жазық плиталарды қолданып жасалған өлшеу құралы ең қарапайым да ыңғайлы құрал ретінде кеңінен қолданылады. Бұл құралды қолданып жылуөткізгіштікті анықтау әдісі 1954 жылы құрылыс материалдарын зерттеу зертханаларының Халықаралық бірлестігінде (RILEM) стандарттық әдіс ретінде қабылданған. Бұл әдіс өткен ғасырдың алпысыншы-сексенінші жылдары алдыңғы қатарлы метрологиялық зертханаларда эталондық өлшеулер үшін пайдаланылды.

Әртүрлі материалдардың жылуөткізгіштігін анықтаудың басқа да замануи тәсілдері көп [8] . Олардың бәріне ортақ бір жағдай - анықталатын негізгі шама ретінде зерттелетін заттың қарама қарсы беттеріндегі температура айырмашылығы алынады. Соңғы мәселе нақты есептеулер жүргізу кезінде өте маңызды. Себебі бұл кезде көбінесе кельвин мен Цельсий арқылы анықталған параметрлер қатар жүреді. Ал температуралар айырмашылығы үшін қандай белгілеулер жүйесінде алынса да бәрібір болғандықтан, белгілеулердегі түсініспеушілік өзінен өзі жойылады.

Жылусиымдылық деп нақты жағдайда дененің температурасын бір градусқа көтеру үшін оның қоршаған ортадан алатын жылу мөлшерін айтады.

Жылуалмасу процесінің өту жағдайына байланысты тұрақты көлем кезіндегі жылусиымдылық (C _v ) пен тұрақты қысым кезіндегі жылусиымдылықты (C _p ) өзара ажырату керек. Заттың жылусиымдылығын есептеу жұмыстарының ерекшелігіне байланысты кейде массаның бірлігіне қатысты алынған меншікті шама ретінде - [Дж/(кг·К], кейде зат мөлшерінің бірлігіне қатысты алынған меншікті шама ретінде - [Дж/(моль·К], ал кейде көлемнің бірлігіне қатысты алынған меншікті шама ретінде - [Дж/(м ³ ·К], анықтайды.

Заттың жылусиымдылығын анықтау қажеттігі мынадай екі негізгі фактормен анықталады:

-біріншіден, ол термодинамикада, қатты денелер физикасында заттардың құрамын зерттеу кезінде, өзара әсер күштерін анықтау кезінде, фаза алмасу процесін зерттеуде, қатерлі құбылыстарды зерттеуде және т. б. жағдайларда қажет болатын мәліметтердің құнды көзі болып табылады;

-екіншіден, осы физикалық шаманы білу әртүрлі жылулық процестер мен аппараттарды кәзіргі заман технологиясына сәйкес инженерлік есептеулерден өткізу үшін қажет. Оның үстіне бұл шамалардың дәлдігі қарастырылып отырған конструкциялардың, технологиялардың, олардың өлшемдері мен жұмыс режимдерінің тиімділігіне зор әсер етеді.

Алғаш рет жылусиымдылық туралы түсінікті 1760 жылы Дж. Блекер енгізді және бұл түсінік әрқашан жылу мен калория ұғымдарымен қатар жүрді.

Заттардың жылусиымдылығын жүйелі түрде өлшеу кезеңі XIX ғасырдың орта шенінен басталды деп айтуға болады, себебі 1845 жылы Джоуль сұйықтардың меншікті жылусиымдылығын анықтауға арналған эксперименттер жүргізді. Оның үстіне Джоуль алғаш рет жылусиымдылықты өлшеу үшін калориметрияда дифференциалдық әдісті қолданды. Ол қолданған калориметр өзара бірдей екі ыдыстан тұратын. Ыдыстың біреуіне жылусиымдылығын анықтау керек сұйық құйылса, екіншісінде жай су болатын. Сұйық пен судың массалары бірдей етіп алынады. Ыдыстардың әрқайсысына кедергілері бірдей спирал қойылады. Электр тогын қосқаннан кейін біраз уақыт өткенде судың температурасының ΔТ ₁ өсуі мен сұйықтың температурасының ΔТ ₂ өсуі өлшенді. Егер судың жылусиымдылығын эталон етіп, оны бірге тең деп алса, онда сұйықтың ізделіп отырған меншікті жылусиымдылығы былайша анықталады:

C _X =C _B + ΔТ ₁ / ΔТ ₂ .

Заттардың жылусиымдылығын өлшеу әдістерінің даму тарихының ерекше кезеңі деп 1912 жылы шыққан П. Дебайдың еңбегі жарық көрген уақытты айтуға болады. Ол өз еңбегінде қатты денелердің жылусиымдылығының теориясын келтірді. Осыдан бастап қатты денелердің жылусиымдылығын анықтаудың эксперименталдық әдістері мен өлшеу құралдарының дамуының жаңа кезеңі басталды.

Онтоғызыншы ғасырдың 40-шы жылдарының орта шенінен бастап өлшеу әдістері мен өлшеу құралдары классикалық калориметрлік әдістерден өзгеше әдістер мен құралдар пайда бола бастады. Бірақ бұл жаңа әдістердің бәріне ортақ екі белгі болды:

- жылусыйымдылықты өлшеудің бұл әдістерінің бәрі де жылуөткізгіштіктің дифференциалдық теңдеуін әртүрлі бастапқы және шекаралық шарттар үшін шешуге негізделген;

- бұл әдістердің бәрінде де зерттелуші обьект температурасы Т болатын бастапқы күйден температуасы Т+ΔТ болатын келесі күйге алып келінеді.

Ал бұл әдістердің әртүрлі болатын себебі зерттелуші обьектіні өзара жақын күйлердің бірінен біріне ауыстыру тәсілдері мен температурамен әсер ету тәсілдері әртүрлі болды [8] . Бұл әдістердің бәрін де динамикалық класқа жатқызамыз, себебі олардың негізінде жатқан белгісіз жылусиымдылық пен өлшенетін эксперименталдық шамаларды байланыстыратын теңдеулер жылуөткізгіштіктің бейстационар теңдеуін шешу нәтижесінде алынды. Ал классикалық калориметрияда квазистатикалық әдіс қолданылды.

Табиғатта жылу алмасудың негізгі үш түрі белгілі. Бұл тұтас дененің ішінде өтетін кондуктивті жылу алмасу, сұйық немесе газ түріндегі денемен қатты дененің бетінде өтетін конвективті жылу алмасу және сәулелік жылу алмасу. Сәулелік жылу алмасуға күн сәулесінің радиациялық жылу алмасуын мысалға келтіруге болады. Тұтас денедегі температуралық өрістің қалыптасуына негізінен жылу алмасудың алғашқы екі түрі әсер етеді. Ал оның үшінші түрі тек арнайы жағдайларда ғана ескеріледі.

Қолданбалы есептерде тұтас денедегі жылу алмасу процесі стационарлық және бейстационарлық деп бөлініп, математикалық физиканың эллипс текті немесе парабола текті дфференциалдық теңдеулерімен сипатталады. Дегенмен, табиғаттағы көптеген процестерді уақытқа тәуелсіз деп, басқаша айтқанда стационар деп қарастыруа болады. Мүндай жағдайда стационарлық жылу алмасу процесі Лаплас немесе Пуассон теңдеуімен сипатталады, және оларды шешу үшін Нейман есебі, Дирихле есебі немесе аралас есеп қойылады.

Қатты денелер арасындағы кондуктивті жылу алмасу заңын Фурье мынадай түрде алған [9] :

.

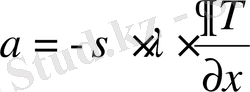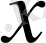Бұл жерде - координаталық осіне перпендикуляр жатқан ауданы арқылы ағып өтетін жылу мөлшері; - дененің координатасы 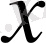болатын нүктесіндегі температура; - жылуөткізгіштік коэффициенті.

Сұйық немесе газ түріндегі денемен қатты дененің бетінде өтетін конвективті жылу алмасу заңын Ньютон алған [9] :

.

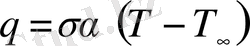Бұл жерде - уақыттың бір өлшемінде ауданы арқылы қоршаған ортаға өтетін жылу ағыны; - қатты дененің бетінің температурасы; - қоршаған ортаның температурасы; - жылу алмасу коэффициенті. Жалпы жағдайда мен коэффициентерінің өздері де температураның функциялары екені белгілі. Бірақ арнайы жағдайларда болмаса мұндай байланыстар ескерілмейді де, олар тұрақты деп алынады.

Өрістер теориясының стационарлық есептерінде сараптама жасалынатын белгілі уақыт кезінде денеде тұрақталған күй орнығады деп есептеледі. Физикалық есептердің келесі бір маңызды класын ізделіп отырған шаманың уақыт бойынша өзгеруін ескеретін есептер құрайды. Бұл есептердің кейбіреулерінде физикалық процестің басталуы мен белгілі бір тұрақты күйі аралығында байқалатын өтпелі кезең болады. Бірақ, тұрақты күйге ешуақытта жетпейтін, бүкіл процесс тек өтпелі кезеңдерден тұратын есептер де кездеседі.

Жазық денедегі стационарлық жылуөткізгіштіктің дифференциалдық теңдеуі былайша жазылады [9-11] :

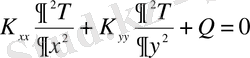. (1. 1)

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс