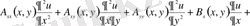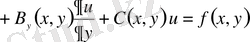ЖЫЛУӨТКІЗГІШТІКТІҢ ТЕҢДЕУЛЕРІНІҢ КЕЙБІР БАСТАПҚЫ-ШЕКТІК ЕСЕПТЕРІН САНДЫҚ ӘДІСТЕРМЕН ШЕШУ

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 59 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Қожа Ахмет Ясауи атындағы Халықаралық қазақ-түрік университеті

Қолжазба құқығында

НАДЫРОВ АБУНАСР АБАЙҰЛЫ

ЖЫЛУӨТКІЗГІШТІКТІҢ ТЕҢДЕУЛЕРІНІҢ КЕЙБІР БАСТАПҚЫ-ШЕКТІК ЕСЕПТЕРІН САНДЫҚ ӘДІСТЕРМЕН ШЕШУ

Мамандығы 6N0501

Математика магистры академиялық дәрежесін алу

үшін дайындалған диссертация

Ғылыми жетекшісі: тех. ғ. к., доцент Қ. Айтбаев

Түркістан 2013

МАЗМҰНЫ

КІРІСПЕ. . . . . .: КІРІСПЕ . . . . . .

3: 3

: 1

КІРІСПЕ. . . . . .:

ШЕКТІ ЭЛЕМЕНТТЕР ӘДІСІН МАТЕМАТИКАЛЫҚ

ФИЗИКА ЕСЕПТЕРІН ШЕШУДЕ ҚОЛДАНУДЫҢ

ТЕОРИЯЛЫҚ НЕГІЗДЕРІ . . .

3: 7

: 1. 1

КІРІСПЕ. . . . . .: Математикалық физика теңдеулері . . .

3: 7

: 1. 1. 1

КІРІСПЕ. . . . . .: Шекаралық және бастапқы шарттар . . .

3: 8

: 1. 1. 2

КІРІСПЕ. . . . . .: Шекаралық шарттар . . .

3: 9

: 1. 1. 3

КІРІСПЕ. . . . . .: Бастапқы шарттар . . .

3: 10

: 1. 1. 4

КІРІСПЕ. . . . . .: Вариациялық принциптер туралы қысқаша түсініктеме . . .

3: 10

: 1. 2

КІРІСПЕ. . . . . .: Шекті элементтер әдісінің теориялық негіздері . . .

3: 11

: 1. 2. 1

КІРІСПЕ. . . . . .: Шекті элементтер әдісінің негізгі концепциясы . . .

3: 12

: 1. 2. 2

КІРІСПЕ. . . . . .: Шекті элементтер әдісінің негізгі этаптары . . .

3: 14

: 1. 2. 3

КІРІСПЕ. . . . . .: Екіөлшемді элементтердің түрлері . . .

3: 15

: 1. 2. 4

КІРІСПЕ. . . . . .: Сызықтық интерполяциялық полиномдар . . .

3: 15

: 1. 2. 5

КІРІСПЕ. . . . . .: Екіөлшемді симплекс-элемент . . .

3: 16

: 1. 2. 6

КІРІСПЕ. . . . . .: Векторлық шамаларды интерполяциялау . . .

3: 19

: 1. 2. 7

КІРІСПЕ. . . . . .: Жергілікті координаталар жүйесі . . .

3: 21

: 1. 2. 8

КІРІСПЕ. . . . . .: Көлемдік

- координаталар . . .

3: 26

: 1. 3

КІРІСПЕ. . . . . .:

Шекті элементтер әдісін стационарлық жылу таралу

есептерінде қолдану . . .

3: 27

: 1. 3. 1

КІРІСПЕ. . . . . .:

Екіөлшемді жылу таралу есебін шекті элементтер әдісімен

шешудің негізгі алгоритмдері . . .

3: 28

: 2

КІРІСПЕ. . . . . .: ТӨРТБҰРЫШТЫ ЭЛЕМЕНТТЕР . . .

3: 41

: 2. 1

КІРІСПЕ. . . . . .: Сызықтық төртбұрышты элемент . . .

3: 41

: 2. 2

КІРІСПЕ. . . . . .: Квадраттық және кубтық төртбұрышты элементтер . . .

3: 46

: 2. 3

КІРІСПЕ. . . . . .: Пішін функцияларының туындыларын есептеу . . .

3: 50

: 2. 4

КІРІСПЕ. . . . . .: Элементтерді анықтайтын қатынастар . . .

3: 54

: 3

КІРІСПЕ. . . . . .:

ТӨРТБҰРЫШТЫ КВАДРАТТЫҚ ЭЛЕМЕНТТІ

ЖЫЛУӨТКІЗГІШТІК ЕСЕБІНЕ ҚОЛДАНУ . . .

3: 68

: 3. 1

КІРІСПЕ. . . . . .: Тұтас жазық денедегі жылуөткізгіштік есебінің қойылымы ……

3: 68

: 3. 2

КІРІСПЕ. . . . . .: Есептеу программасының алгоритмына қысқаша талдау ………

3: 70

: 3. 3

КІРІСПЕ. . . . . .: ABU есептеу программасының жұмысының нәтижелеріне қысқаша cараптама . .

3: 71

КІРІСПЕ. . . . . .: ҚОРЫТЫНДЫ . . .

3: 75

КІРІСПЕ. . . . . .: ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . .

3: 76

КІРІСПЕ

Жұмыстың көкейтестілігі: Ғылым мен техниканың дамыған заманында физика мен математика саласында классикалық аналитикалық әдістермен қатар ғылымның қолданбалы бөлігі де қатты дамып келе жатыр. Қолданбалы математика негізінен сандық әдістерге сүйенеді. Ғылымның бұл саласының соңғы жылдары ғарыштап дамуына есептеу техникасының және әртүрлі программалау жүйелерінің дамуы да қатты әсер етуде. Кең таралған сандық әдістерге шекті айырымдар әдісі, шекаралық интегралдық теңдеулер әдісі және шекті элементтер әдісі жатады. Аталған әдістердің алғашқы екеуі зерттеу аймағы біртекті болған кезде қолданылады, себебі бұл әдістерде анықтаушы дифференциалдық теңдеулер бүкіл зерттеу аймағы үшін бірден құрылады. Оның үстіне бұл әдістерде зерттеу аймағының геометриясы да аналитикалық түрде сипаттауға ыңғайлы болғаны шарт. Ал келесі сандық әдіс - шекті элементтер әдісіне аталған шектеулер бөгет бола алмайды. Шекті элементтер әдісі әсіресе математикалық физиканың эллипс текті, парабола текті немесе гипербола текті дифферециалдық теңдеулермен сипатталатын процестерді геометриясы күрделі және біртекті емес аймақтар үшін зерттеуге қолайлы. Мысалы, шекті элементтер әдісімен температура, қысым және сол сияқты скалярлық өрістерді өте үлкен дәлдікпен зерттеуге болады. Бұл кезде шекті элементтің ең қарапайым түрі, үшбұрышты симплекс элементтерді қолданса жеткілікті. Алайда техниканың кейбір есептерінде, атап айтқанда тұтас денедегі кернеулі-деформациялық күйді зерттеген кезде көп жағдайда шешімнің дәлдігі жеткіліксіз болып жатады. Мұндай жағдай әсіресе зерттеу аймағында сингулярлық нүктелер бар кезде градиенті жоғары шамалардың аталған нүктелер маңындағы өзгерісін байқамай қалуға алып келеді. Аталған жағдайдан шығудың ең ұтымды жолы жоғары ретті интерполяциялық полиномдарды қолдану. Мұндай полиномдарды үшбұрышты шекті элементтерде де қолдануға болады. Бірақ төрт түйінді, сегіз және он екі түйінді төртбұрышты шекті элементтерді қолдану өте жақсы нәтиже беретінін өмірлік тәжірибе көрсетіп отыр.

Диссертациялық жұмыста шекті элементтер әдісінің теориялық негіздеріне шолу жасалынған және үшбұрышты симплекс элементтердің осал жерлеріне сараптама жасалынған. Содан кейін төртбұрышты, төрт және сегіз түйінді элементтерді қолданудың теориясы ашылып жазылып, оларды есептеу практикасында қолдануға мысалдар келтірілген. Төртбұрышты, біртекті жазық денеде қалыптасатын температуралық өрісті квадраттық элемент деп аталатын төртбұрышты сегіз түйінді шекті элементті қолданып зерттеу есебі қойылған. Есептің шекті элементтер әдісі негізінде құрылған алгоритмін компьютерде жүзеге асыру үшін жоғары деңгейлі MATLAB жүйесі таңдалған. Диссертациялық жұмыста аталған жүйеде жасалынған есептеу программасының негізгі блоктарына терең талдау жасалынған. Графикалық түрде алынған нәтижелер әртүрлі шекаралық шарттар үшін келтіріліп, сарапталған.

Жұмыстың идеясы :

Шекті элементтер әдісімен математикалық физика есептерін шешу жолдарын сараптау;
Шекті элементтер әдісіндегі шекаралық және бастапқы шарттардың түрлеріне шолу жасау;
Жоғары ретті интерполяциялық полиномдарды қолдану ерекшеліктерін терең зерттеу.

Зерттеулердің мақсаты: Математикалық физика есептерін шекті элементтер әдісімен шешу барысында кейбір есептердің, әсіресе тұтас денелерде қалыптасатын кернеулі-деформациялық күйді анықтау есебінде сызықтық симплекс элемент арқылы алынған неәтижелердің дәлдігі жеткіліксіз болып жатады. Бұл кемшілікті жоюдың бірден бір жолы жоғары дәрежелі интерполяциялық полиномдарды қолдану. Диссертациялық жұмыстың мақсаты жоғары дәрежелі полиномдарды шекті элементтер әдісінде қолданудың ықшам алгоритмын MATLAB жүйесінде жасап шығу.

Қойылған мақсатқа сәйкес диссертациялық жұмыста келесі жұмыстар атқарылды:

- математикалық физика есептеріне сараптама жасалынады;

- шекті элементтер әдісінің теориялық негіздеріне шолу жасалынады;

- тұтас денедегі жылуөткізгіштік есебін шекті элементтер әдісімен симплекс элементтерді қолданып шешудің алгоритмына толық сараптама жасалды;

- тұтас денедегі жылуөткізгіштік есебін шекті элементтер әдісімен шешу кезінде жоғары ретті интерполяциялық полиномдарды қолдану жолдары анықталып, арнайы есептеу программасы MATLAB жүйесінде жасалынды және нақты есепте программаның жұмысы тексерілді. Алынған сандық нәтижелер графикалық түрде көрсетіліп, оларға сараптама жасалынды.

Зерттеу әдістері. Матрицалар алгебрасының ережелері мен әдістерін MATLAB жүйесінде тиімді қолдану үшін нақты есепті шекті элементтер әдісін қолданып шешу алгоритмы жасалды.

Қорғауға шығарылған ғылыми тұжырымдар мен нәтижелер :

- математикалық физика есептерін шекті элементтер әдісімен шешкен кезде шекаралық және бастапқы шарттарды тағайындау ерекшеліктері;

- жылуөткізгіштік матрицасын құру барысында қажет болатын интегралдарды есептеу жұмысын автоматтандыру жолдары;

- тұтас денедегі жылуөткізгіштік есебін шекті элементтер әдісімен шешу барысында симплекс элементтерді қолдану алгоритмы;

- тұтас денедегі жылуөткізгіштік есебін шекті элементтер әдісімен шешу барысында жоғары ретті интерполяциялық полиномдарды қолданып құрылған есептеу алгоритмының жұмысын нақты мысалда тексеру.

Автордың жеке үлесі:

- зерттеулердің мақсаты анықталып, есептер қойылды;

- тұтас денедегі жылуөткізгіштік есебін шекті элементтер әдісімен шешу барысында жылуөткізгіштік матрицасын симплекс элемент, квадраттық және кубтық төртбұрышты элементтерді қолданып құрастыру жолдары игерілді;

- тұтас денедегі жылуөткізгіштік есебін шекті элементтер әдісімен шешу барысында квадраттық төртбұрышты элементті қолданудың есептеу программасы құрылды.

Ғылыми жаңалықтар:

- тұтас денедегі жылуөткізгіштік есебін шекті элементтер әдісімен шешу барысында төртбұрышты квадраттық элементтерді қолдану жолдары анықталды;

- тұтас денедегі температуралық өрістің шекаралық шарттарға тәуелділігі зерттелді.

Алынған нәтижелердің ғылыми негізділігі:

Қолданбалы физика, механика және математика есептерінде кеңінен қолданылып жүрген шекті элементтер әдісін дамыту мақсатында зерттеулер жүргізілді. Зерттеулер барысында теориялық негіздері көпке белгілі материалдар қолданылды. Зерттеулердің сандық нәтижелері жоғары деңгейлі программалаудың MATLAB жүйесінде алынды.

Жұмыстың нәтижелерінің тексерілуі:

Жұмыстың негізгі тұжырымдары мен нәтижелері 2012 жылы ХҚТУ ұйымдастырған “Өзбекәлі Жәнібеков оқулары” атты III рес. ғыл. -тәжіриб. ғылыми конференцияда баяндалды.

Жариялануы: Диссертациялық жұмыстың тақырыбы бойынша «Шекті элементтер әдісінде жоғары ретті элементтерді қолдану жолдары» деген атпен «Өзбекәлі Жәнібеков оқулары - 2012». III рес. ғыл. -тәжіриб. конференция материалдарында жеке мақала түрінде жарық көрді. Сонымен бірге ХҚТУ Хабаршысы журналының 2013 жылғы №1(81) санында «Вычисление определителя матрицы Якоби для изопараметрических и субпараметрических элементов» атты мақаласы жарияланды.

Диссертациялық жұмыстың құрылымы: диссертациялық жұмыс кіріспеден, үш бөлімнен тұратын негізгі мәтіннен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.

Бірінші бөлімде математикалық физика теңдеулерін шешу барысында тағайыналатын бастапқы және шекаралық шарттардың түрлеріне талдау жасылынды. Бөлімнің екінші жартысында шекті элементтер әдісінің теориялық негіздеріне шолу жасалынды. Шекті элементтер әдісін симплекс элементтерді қолданып жылөткізгіштік есебін шешудің алгоритмына талдау жасалында.

Екінші бөлімде шекті элементтер әдісінде жоғары дәрежелі интерполяциялық полиномдарды қолдану жолдары қарастырылды. Аталған элементтердің түрлері келтірілді және оларды қолданып элементтердің жылуөткізгіштік матрицаларын құрған кезде қажет болатын интегралдарды сандық әдістермен есептеу жолдары келтірілді. Гаусс-Лежандр квадратурасын пайдаланып элементтерді анықтайтын қатынастардағы интегралдарды есептеудің толық алгоритмы келтірілді. Квадраттық және кубтық төртбұрышты элементтердің пішін функцияларын алу жолдары келтірілді.

Үшінші бөлімде шекті элементтер әдісінде жоғары ретті интерполяциялық полиномды пайдаланып есеп шығаруға нақты мысал қарастырылды. Алынған сандық нәтижелер графикалық түрде келтіріліп, оларға сараптама жасалынды. Есептің шешімінің шекаралық шарттарға тәуелділік деңгейіне талдау жасалынды.

1 ШЕКТІ ЭЛЕМЕНТТЕР ӘДІСІН МАТЕМАТИКАЛЫҚ ФИЗИКА ЕСЕПТЕРІН ШЕШУДЕ ҚОЛДАНУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

Диссертациялық жұмыстың тақырыбынан жұмыстың негізгі мақсаты шекті элементтер әдісін математикалық физика есептерін шешуге сандық әдістердің бірін таңдап, нақты шектік септі шешу екенін көреміз. Алдымен математикалық физика есептері туралы түсініктерге шолу жасалып, есептердің шекаралық және бастапқы шарттары туралы, шекті элементтер әдісін қолдануға мүмкіндік беретін вариациялық принциптер туралы түсініктерді айқындап алу керек.

1. 1 МАТЕМАТИКАЛЫҚ ФИЗИКА ТЕҢДЕУЛЕРІ

Қазіргі заманда ғылым мен техниканың көптеген мәселелері математикалық физика есептерін шешумен байланысты. Жылуөткізгіштік, диффузия, электрлік статика, электрлік динамика, сұйықтардың ағысы, электр тогының тығыздығының таралуы, қатты денелердің деформациялануы және тағы басқа көптеген есептер математикалық физика есептеріне жатады.

Мұндай есептер шекаралық және бастапқы шарттармен бірге қарастырылатын дербес туындылы дифференциалдық теңдеулермен сипатталады. Әдетте қолданбалы математика ғылымында қарастырылатын дифференциалдық теңдеулердің реті екіншіден аспайды. Себебі, осындай теңдеулер сипаттайтын физикалық құбылыстардың өзі өте үлкен диапазон құрайды. Оның үстіне, диссертациялық жұмыста келтірілетін әдістерді бұдан да жоғары ретті дифференциалдық теңдеулерге қолдануға болады. Жалпы жағдайда n тәуелсіз айнымалының екінші реттегі дербес туындылы дифференциалдық теңдеуі мынадай түрде болады [1] :

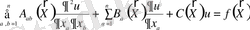Бұл жерде 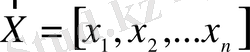- тәуелсіз айнымалылардың векторы (матрица-қатар) ; -тәуелсіз айнымалылардың белгісіз функциясы; 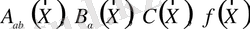- тәуелсіз айнымалылардың нақты функциялары.

(1. 1) -ші теңдеуді үш стандартты канондық түрлердің біреуіне әрқашанда келтіруге болады. 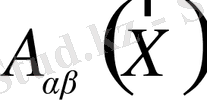шамаларының өзара қатынасына байланысты теңдеулерді 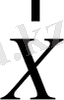нүктесіндегі эллипстік, параболалық немесе гиперболалық текті теңдеу деп бөледі. Мысалы, тәуелсіз 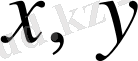айнымалыларының екінші ретті дифференциалдық

теңдеуінің тегі дискриминант деп аталатын келесі шаманың мәні арқылы анықталады:

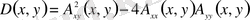Егер 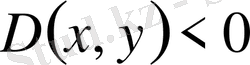болса, онда дифференциалдық теңдеу 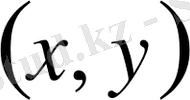нүктесінде эллипстік теңдеу болады.

Егер 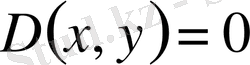болса, онда дифференциалдық теңдеу 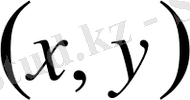нүктесінде параболалық теңдеу болады.

Егер 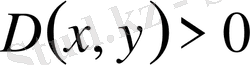болса, онда дифференциалдық теңдеу 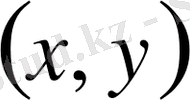нүктесінде гиперболалық теңдеу болады.

Егер 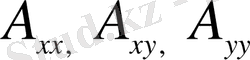коэффициенттері тұрақты болса және дискриминант 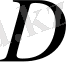координатаға тәуелсіз болса, онда дискриминанттың таңбасына байланысты теңдеу толық эллипстік, толық параболалық немесе толық гиперболалық болып бөлінеді [1] .

1. 1. 1 ШЕКАРАЛЫҚ ЖӘНЕ БАСТАПҚЫ ШАРТТАР

Жоғары математика курсынан әдетте дифференциалдық теңдеулердің шексіз көп шешімдері болатыны белгілі. Себебі, дифференциалдық теңдеулерді интегралдау кезінде пайда болатын белгісіз константалардың кез келген мәндері берілген дифференциалдық теңдеулерді қанағаттандырады [2] .

Математикалық физика есептерін шешу белгілі бір физикалық шамалардың координаталар мен уақытқа тәуелділігін анықтаумен байланысты. Алынған шешім әрқашан жалғызмәнді, шекті және үзіліссіз болу керек [2] . Басқаша айтқанда, математикалық физиканың кез келген есебі жалғыз ғана шешімді (егер ол бар болса) табуды талап етеді. Сондықтан физикалық есептің математикалық қойылуы ізделіп отырған функцияны қарастырылып отырған аймақтың ішкі нүктелерінде сипаттайтын негізгі теңдеулермен бірге (дербес туындылы дифференциалдық теңдеулер) қосымша теңдеулерді де қамтуы керек. Қосымша теңдеулер (дифференциалдық немесе алгебралық) белгісіз функцияның уақыттың әрбір сәтіндегі шекаралық мәндерін және оның уақыттың алғашқы сәтіндегі қарастырылып отырған аймақтың ішкі нүктелеріндегі мәндерін сипаттайды (Коши есебі) . Аталған қосымша теңдеулер есептің шекаралық және бастапқы шарттары деп аталады.

1. 1. 2 ШЕКАРАЛЫҚ ШАРТТАР

Кезкелген 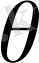аймағында математикалық физика теңдеуімен сипатталатын белгілі бір есепті шешу қажет болсын делік. Есептің жалғыз ғана шешімін табу үшін шекаралық шарт, басқаша айтқанда, белгісіз айнымалылардың 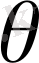аймағының шекаралық бөлігіндегі мәндері берілген болуы керек.

Егер 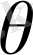аймағы үшөлшемді кеңістіктегі кезкелген көлем болса, онда берілген көлемді қоршап тұрған тұйық бет болады. Егер 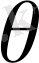аймағы екіөлшемді кеңістіктегі кезкелген бет болса, онда берілген бетті қоршап тұрған тұйық контур болады. Ең соңында, егер 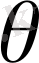аймағы бірөлшемді кеңістіктегі кезкелген кесінді болса, онда берілген кесіндінің екі шеткі нүктесі болады.

Шекаралық шарттарды беретін теңдеулердің түріне қарап оларды бірінші текті (Дирихле шарттары), екінші текті (Нейман шарттары) және үшінші текті (аралас шарттар) деп бөледі [1] .

Бірінші текті шекаралық шарттар немесе Дирихленің шекаралық есебі былайша беріледі:

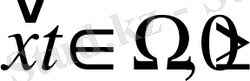болғанда .

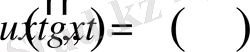Бұл жерде 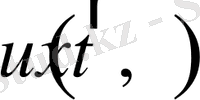- ізделіп отырған белгісіз 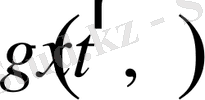функция; - шекарасында берілген кезкелген функция; 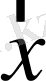- шекаралық нүктенің кеңістіктегі координаталары (мысалы, үшөлшемді кеңістік үшін 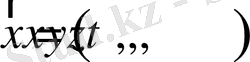) ; - уақыт.

Егер жылуөткізгіштік есебі қарастырылып отырса, онда бірінші текті шекаралық шарт шекарасындағы температураны береді. Ток өткізбейтін ортадағы электростатикалық өрістің таралуы есебінде бірінші текті шекаралық шарт шекарасындағы электр потенциалын береді және т. б.

Екінші текті шекаралық шарттар немесе Нейманның шекаралық есебі былайша беріледі:

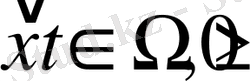болғанда .

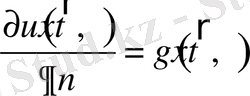Бұл жерде - шекарасының ішкі нормалі.

Басқаша айтқанда, Нейман шарттары шекарадағы ағынды, дәлірек айтсақ, ағын векторының шекараға түсетін нормальға проекциясын береді. Мысалы, жылуөткізгіштік есептерінде екінші текті шекаралық шарттар жылу ағынын береді, ал ток өткізбейтін ортада электростатикалық өрістің таралуы туралы есепте - электр өрісінің кернеулігінің векторының шекараға түсетін нормальға проекциясын береді және т. б.

Үшінші текті шекаралық шарттар Дирихле мен Нейман есептерінің жалпыланған түріне жатады және былайша жазылады:

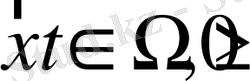болғанда .

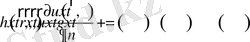Бұл жерде - координаталар мен уақыттың белгілі функциялары. Мысалы, жылу есептерінде үшінші текті шекаралық шарттар шекарадағы конвективті жылу алмасу мен сәулелік жылу алмасуды беруге пайдаланылады.

1. 1. 3 БАСТАПҚЫ ШАРТТАР

Бейстационар, уақыт бойынша өзгеріп отыратын, физикалық процестерді сипаттайтын есптердің жалғыз ғана шешімін табу үшін шекаралық шарттармен бірге бастапқы шарттарды да беру керек. Бастапқы шарттар айнымалылардың немесе олардың градиенттерінің қарастырылып отырған 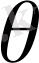аймақтың шекаралық нүктелерінен бөлек ішкі нүктелеріндегі уақыттың бастапқы сәтіндегі мәндерін қамтиды :

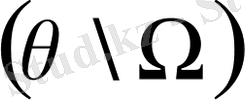болғанда ;

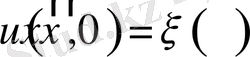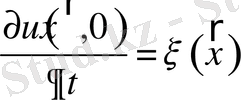болғанда .

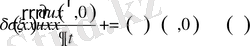Бұл жерде 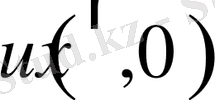- ізделіп отырған белгісіз функцияның уақыттың бастапқы сәтіндегі мәні; - координаталардың белгілі функциялары.

Шекаралық шарттар сияқты, бастапқы шарттардың саны да дифференциалдық теңдеулердегі уақыт бойынша туындылардың ең үлкен ретімен анықталады [3] .

1. 1. 4 ВАРИАЦИЯЛЫҚ ПРИНЦИПТЕР ТУРАЛЫ ҚЫСҚАША

ТҮСІНІКТЕМЕ

Математикалық физика есептері көп жағдайда жоғары ретті дербес туындылы дифференциалдық теңдеулермен өрнектеледі. Бұл теңдеулер күнделікті өмірде болып жататын физикалық, химиялық және т. б. күрделі процестерді математикалық тұрғыдан сипаттайды. Әрине, мұндай дифференциалдық теңдеулердің аналитикалық шешімі қолдануға ыңғайлы болатыны даусыз. Бірақ олардың санаулы түрлерінің ғана аналитикалық шешімі табылады. Соның өзінде нақты есептің негізгі табиғи шарттарына көптеген шектеулер мен жеңілдетуші гипотезалар енгізіледі. Мысалы, біртекті емес, бірнеше бөліктен тұратын, геометриясы күрделі тұтас дененің кернеулі-деформациялық күйін сипаттайтын дифференциалдық теңдеудің аналитикалық шешімін табу өте күрделі математикалық мәселе. Мұндай кезде берілген дифференциалдық теңдеу вариациялық принциптердің көмегімен шешімі жеңіл табылатын басқа дифференциалдық, немесе алгебралық теңдеумен алмастырылады.

Алғаш рет вариациялық принциптерді дербес туындылы дифференциалдық теңдеулерді шешуге қолданған Эйлер деп есептеледі. Вариациялық принципті дербес туындылы дифференциалдық теңдеуді шешуге қолдану үшін алдымен аталған дифференциалдық теңдеуге сәйкес функционал деп аталатын интегралдық шама құрастырылуы керек. Бұл әрине зерттеліп отырған процестің табиғи мағынасын толық түсінбей мүмкін емес. Мысалы, тұтас денеде қалыптасатын температуралық өріс (стационарлық, немесе бейстационарлық) пен жерасты суларының ағысын сипаттайтын дифференциалдық теңдеулер бірдей түрде (эллипс, немесе парабола тектес) жазылады. Ал оларға сәйкес функционалдар әртүрлі болады.

Функционалдарға экстремум беретін функцияны іздеу үшін вариациялық принципті қолданған кезде Эйлер мынадай қағиданы ұстанған. Егер тәуелсіз бір айнымалының кез келген функциясының экстремумын табу үшін функцияның тәуелсіз айнымалы бойынша туындысын нолге теңестіру керек болса, осы әдісті функционалдарға да қолдануға болады. Себебі екі жағдайда да экстремалдық нүкте (функция) маңында функция (функционал) өзінің өзгеру жылдамдығын күрт азайтады, ал шексіздік жағдайында мүлдем доғарады. Демек, оның вариациясы нолге ұмтылады. Сондықтан Эйлер функционалға экстремум беретін функцияны тәуелсіз айнымалыға айналдырған.

Физика ғылымында вариациялық принциптер көптеп саналады. Мысалы, тұтас денедегі температуралық өріс өзгеруін доғарып, стационарлық күйге көшкен кезде денеде жинақталатын толық жылу мөлшері өзінің ең кіші мәніне жетеді. Сол сияқты, сыртқы күштердің әсерінен денеде пайда болатын деформациялардың толық потенциалдық энергиясы дене теп теңдік қалыпқа көшкен кезде өзінің ең кіші мәнін қабылдайды. Аталған шамаларды анықталған интеграл түрінде сипаттау арқылы қажетті функционалдар алынады. Алынған функционалдарды минималдау арқылы оларға минимум беретін функция табылады. Ал өз кезегінде, бұл функция бастапқы дифференциалдық теңдеудің де шешімі болады. Келтірілген мысалдардан зерттеліп отырған процеске сәйкес функционал құру үшін оның физикалық мағынасын толық түсіну қажет екені түсінікті болып қалады.

1. 2 ШЕКТІ ЭЛЕМЕНТТЕР ӘДІСІНІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

Шекті элементтер әдісі физика мен техникада кездесетін дифференциалдық теңдеулерді сандық әдіспен шешуге арналған. Бұл әдіс космостық зерттеулерден туған есептерді шешуге байланысты пайда болған (1950 ж) . Алғаш рет ол Тернердің, Клуждың, Мартин мен Топптың еңбектерінде жарық көрді [4] . Осының артынан әдісті құрылыс механикасы мен тұтас денелердің механикасы есептерінде қолданған бірқатар еңбектер пайда болды. Әдістің теориялық негізделуіне 1963 жылы Мелош [5] көп еңбек сіңірді. Ол шекті элементтер әдісінің осыған дейін кеңінен таралған Рэлей-Ритц әдісінің бір варианты екенін дәлелдеді. Құрылыс механикасында шекті элементтер әдісі потенциалдық энергияны минималдау арқылы есепті тепетеңдіктің сызықтық алгебралық теңдеулер жүйесіне алып келеді.

Шекті элементтер әдісінің минималдау процедурасымен байланысы әдісті техниканың басқа салаларындағы көптеген есептерді шешуге кеңінен пайдалануға мүмкіндік берді. Әдіс Лаплас немесе Пуассон теңдеулерімен сипатталатын есептерді шешуге қолданылды. Бұл теңдеулерді шешу де белгілі бір функционалдарды минималдаумен байланысты. Алғашқы басылымдарда [6, 7] шекті элементтер әдісімен жылу таралу есептері шешіліп жүрді. Кейіннен әдіс гидромеханиканың есептеріне, атап айтқанда, қуысты ортада сұйықтардың ағу процестерін зерттеуге қолданыла бастады.

Шекті элементтер әдісін қолдану саласының кеңуіне құрылыс механикасында, жылу таралу процестерінде, гидромеханикада қолданылатын теңдеулер Галеркин әдісімен немесе ең кіші квадраттар тәсілімен оңай алынатыны дәлелденуі көп ықпал етті [8, 9] . Бұл фактор әдісті теориялық жағынан негіздеуге көмектесіп, оны кез келген дифференциалдық теңдеулерді шешуде қолдануға мүмкіндік берді. Айта кету керек, кеңірек жұргізілген теориялық зерттеулер физикалық есептерді шешуде вариациялық принциптерді барлық уақытта қолданудың қажеті жоқ екенін дәлелдейді.

Шекті элементтер әдісі құрылыс механикасының есептерін шешуге арналған сандық әдістен барлық дифференциалдық теңдеулерді немесе олардың жүйелерін шешуге арналған жалпы әдіске айналды. Бұл прогреске бірнеше онжылдық аумағында есептеу машиналарының күрт дамуына, ұшатын аппараттарды дәлірек зерттеу қажеттігіне, космостық зерттеулердің кеңінен дамуына байланысты қол жетті. Қазіргі кезде шекті элементтер әдісі самолеттер, ракеталар жасау саласында, атом реакторларын жобалауда және т. б. күрделі салаларда кеңінен қолданылады.