Тарихи есептер және теңдеулер: алгебра тарихы мен оқу-әдістемелік қолданылуы


Жоспар:
- Кіріспе
- Негізгі бөлімҚызықты тарихи есептер
- Қорытынды
- Пайдаланылған әдебиеттер тізімі
Кіріспе
Алгебра практикалық есептерді теңдеулер жәрдемімен шығару тәсілдерінен туған. Теңдеулер жөніндегі ілім бүгінге дейін алгебраның мектептік курсының негізгі мазмұны болып табылады. Бірақ теңдеулерді шешу үшін бірмүшелерге, көпмүшелерге және алгебралық бөлшектерге амалдар қолдана білу керек, көпмүшелерді жіктей білуді, жақшаларды ашуды, бөлшектерді ортақ бөлімге келтіруді т. с. с. білу керек. Сөйтіп, теңдеулер жөніндегі ілімді амалдардың заңдары туралы ілімсіз игеру мүмкін емес. Теңдеулерді шешу үшін қолданылатын амалдар нақтысында сандарға қолданылады, өйткені элементар алгебрада әріптер сандарды белгілеу үшін қолданылады.
Ежелгі вавилондықтардың табылған сына жазулы текстеріне қарағанда кейбір көбейту формулалары (қосындының квадраты, айырманың квадраты, қосындының айырмаға көбейтіндісі) тіпті бұдан 4000 жылдай бұрынғы кездің өзінде-ақ белгілі болған. Вавилондықтардан басқа да ертедегі халықтар бұл формулаларды әрине, бізше, символикалық түрде емес, сөзбен баяндалған түрінде немесе мысалы, ертедегі гректерше, геометриялық формада білген.
Ежелгі Греция ғалымдары шамаларды сандар немесе әріптер арқылы өрнектемей, түзу кесінділері арқылы кескіндеп көрсеткен, ал кесінділерді бір әріппен немес олардың ұштарына қойылған екі әріппен белгілеген.
Егер де тарихқа үнілетін болсақ, практикалық есептерді шығарудың алгебралық әдістерінің бастамасы ежелгі ғылым әлемімен байланысты. Сол кездің өзінде де теңдеулер құруды талап ететін есептер пайда бола бастады. Алғашқыда мұндай есептерді шығару үшін арифметикалық әдістер қолданылды. Одан әрі алгебралық жағын қарастыру қалыптаса бастады. Қазіргі уақытқа дейінгі теңдеулер дамуында әр түрлі әдістердің өзгеріп жаңарып отыруы осы ұғымдардың нақтылануы мен басқа да математиканың бөлімдерімен байланысын атап өтуге болады. Бұл процесте теңдеу алгебралық ұғымдар жүйесіндегі мән маңызды роль атқарады. Алгебраның дамуы теңдеуді алгебраның негізгі ұғымы ретінде үш негізге негізделді:
а) теңдеулер мәтінді есептерді шығарудың құралы ретінде;
б) теңдеулер алгебрадағы оқу объектісі бола алатын ерекше бір формула ретінде;
в) теңдеулер кеңістіктегі (жазықтықтағы) координата нүктелерін немесе сандарды жаналамай анықтайтын формула ретінде. Сол себептен теңдеу жалпы математикалық ұғым жағынан көп аспекті. Теңдеу ұғымына байланысты теңдеудің маңыздылығы мен кең көлемділігіне қарап оны оқып үйрену қазіргі математикалық әдісте мазмұнды-әдістемелік негізде теңдеулер ұйымдастырылған.
Төменде осы теңдеулер арқылы шығарылатын тарихи есептерді қарастырамыз.
Қызықты тарихи есептер.
Математика сабақтарында тарихи мағлұматтарға шолу негізгі өтетін материалдарға сай болуы керек. Мысалы. Оқушыларды геометриялық прогрессиямен таныстырған кезде оларға мынадай есеп - аңызды айтға болады: Бірде Үндістанның Шерам деген патшасы шахмат ойынын ойлап тапқан Сетаны шақыртыпты да қандай тілегі барын сұрапты. Сета шахмат тақтасының бірінші шаршысында бидайдың бір дәнін, екіншісіне 2 дән, үшіншіге 4 дән, ж»не т. с. с. қойып шыққанда қанша дән болса соншасын берудің сұраған екен. Ал патша Сетаның «қарапайым өтінішін» орындауға қанша тырысқанмен шамасы да, байлығы да жетпепті. Бұл есепте 1, 2, 2 2 , 2 3 . . . , 2 63 геометриялық прогрессия құрайтын сандардың қосындысы туралы айтылып отыр. Сөйтсек ол қосынды мынаған тең болады екен:
2 64 -1=18446744073790551615.
Ал мұндай дән санын ауданы жер бетінен 2000 есе артық болатын планета астығынан ғана алуға болатынын айтып геометриялық прогрессияның «құдіретін» танытып өткен жөн.
Математикалық қолданбалық мағынасы туралы оқушылардың танымын қалыптастырудың маңызы зор. Мысалы, математиканың сәулет өнерінде қолданылуы туралы мысалдар келтіріп өтудің еш артықшылығы жоқ.
Сәулет өнеріндегі көркемдік образ жасауға себеп болатын құралдардың бірі - пропорция. Пропорцияны пайдаланудың ертедегі Грециямен Римнің, орта ғасырдағы Азия, Еуропа сәулетшілерінің жұмыстарынан көптеп кездестіреміз.
Қазіргі сәулет өнерінде әдемілік, сұлулық, салтанаттылық пропорциялармен қамтамасыз етілетін көңіл аудара қарасақ қай-қайсымыз да байқай аламыз. Мысалы. «Алтын қима», «Құдайшыл пропорция» деген атпен көркемдік эталоны болып танылған, қысқасының ұзынына қатынасы, ұзынынынң барлық кесіндіге, қатынасындай болған кесіндіні екі бөлікке бөлуді қарастырайық:
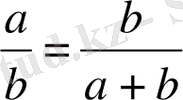
«Құдайшыл пропорция» көптеген зерттеушілер жұмысының қорытындысына қарағанда табиғатта һнерде соның ішінде әр түрлі мемлекеттермен елдердің сәулетінде жиі кездеседі. Үйлердің вертикаль орналасқан элементтерінің пропорцияларында геомтериялық кесінділердің ұқсастығы кеңінен қолданылады.
Мұғалімнің басты міндеттерінің бірі - оқушыларға пәннің көркемділігін көрсетіп, олардың танымдылық ықласын дамытуға қолданылуында. Атап айтқанда мұғалім теореманы қызықты жолдармен дәлелдеуге болатынын және есептерді шешудің нақышты жолдарын көрсете білуі керек. Бұл тұрғыдан теомреманың дәлелдеуінің көркемділігін оның қысқа түрлендірулер арқылы дәлелдеу идеясы жетік, жай түрде болып, ізделінің отырған, мақсатта қарапайым жолмен жетуден көруге болады. Мысалы:
- теңсіздігін дәлелдеу керек.
Бұл есептің шешімін өте ұзақ ңздеп тұжырымды қорытындыға кенеттен бір шешім «шыға» келмесе келе алмауымыз мүмкін. Ал егер бірінші қосылғыштағы соңғы цифрды 9-ға, екңншң қосылғыштағыны 8-ге ауыстырсақ, онда түбірлерді таба отырып, 3+2=5 депаламыз. Олай болса, берілген теңсіздік ақиқат.
- Х17-12х16+12х15-12х14+ . . . -12х2+12х-1 өрнегін х=11 болғанда есептеу керек болсын . Оны есептеу үшін өрнекке бірден х=11 мәнін қойып, қосындылардың дәйекті түрін қарастырамыз:
11 17 -12*11 16 =11 16 (11-12) =-11 16
-11+12*11 15 =11 15 (11+12) =11 15
11 15 -12*11 14 =11 14 (11-12) =-11 14
11-1=10
Математиканың көптеген тақырыптары оқушылардың көркемдікті, әдемілікті сезінуін тәрбиелеуге әсерін тигізеді. Мысалы. «Симметрия» темасы. Табиғаттағы көптеген формалардың көркемдік негізін симметрия құрайды. Ал математика - симметрияның негізгі қайнар көзі.
№1. Эйлер есебі.
Бір санның 4-ші дәрежесін сол санның жартысына бөлгенде және
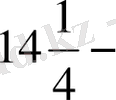 ге
ге
арттырғанда 100-ге тең болу керек. Сол санды тап.
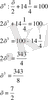
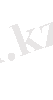
Жауабы:
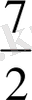 ;
;
№2. Үш адам 24000 ливрға үй сатып алғысы келді. Олар былай келісті: біріншісі жарты ақшасын береді; екіншісі үштен бірін береді, ал үшіншісі қалған бөлігін береді. Әрқайсысы қанша бермек?
I-ші:
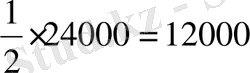
II-ші:
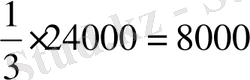
III-ші:
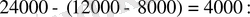
Жауабы:
№3. Бір топ қаз ұшып барады, оларға бір қаз қарсы ұшып келе жатып: «Жүз қазға бір сәлем!» - депті. Топ қаз оған былай деп жауап беріпті: «Жоқ біз жүз емеспіз! Егер бізге тағы осынша қосылса, тағы соның жартысындай, тағы соның ширегіндей, оның үстіне сен қазым, бізге қосылсаң, біз тура жүз қаз боламыз» Олар қанша болған еді?
Шешуі: қаз саны - х
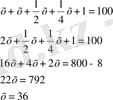
Жауабы:
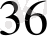 қаз.
қаз.
№4. Бехаэддин есебі.
Өзінің үштен екісіне және бірлікке арттырылған сан 10-ға тең. Сол санды табу керек.
Шешуі: Ізделінді сан - х
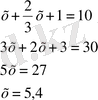
Жауабы:
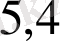
№5. «Үш адам ақша ұтып алған. I адамға осы соманың
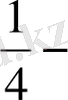 і, II адамға осы
і, II адамға осы
соманың
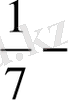 і, III адамға 17 флорин тиді. Ұтыстың шамасы қандай болған?»
і, III адамға 17 флорин тиді. Ұтыстың шамасы қандай болған?»
Шешуі: Ұтыс шамасы - х
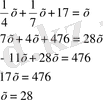
Жауабы:
 флорин.
флорин.
№6. «Бір адам жыл аяғына дейін киім және 10 флорин алмақшы болып жалданды. Бірақ 7 ай өткен соң жұмысты тоқтатты да, есеп айырысқанда киім және 2 флорин ақша алды. Киім қаншаға бағаланған?»
Шешуі: киім - х
1 жылда -
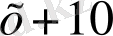
7 айда -

 айға = 1, 6
айға = 1, 6
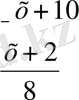
1, 6 · 12 = 19, 2 ( 1жылда)
х + 10 = 19, 2
х = 9, 2
Жауабы: 9, 2.
№7. «Тоғыз кітаптағы математикадан» есеп. Бірнеше адам бірлесіп тауық сатып алған. Егер әр адам 9-дан (ақша бірлігі) берсе, онда 11 қалады, ал егер әрқайсысы 6-дан берсе, 16-сы жетпей қалады. Адам саны мен тауықтың құнын табу керек».
Шешуі:
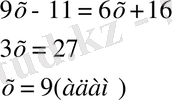
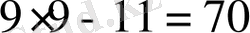
№8. «Егер бір санды 20-ға қоссақ және сол санды 100-ден алсақ, сонда шыққан қосынды сонда шыққан айыпмадан 4 есе артық болады. Белгісізді табу керек. »
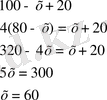
Жауабы: 60.
№9.
Акмим папирусынан
(VI ғ. ) есеп: «Бір адам қазынаның
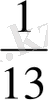 - ін алды. Одан қалғанының
- ін алды. Одан қалғанының
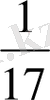 - ін екінші біреу алды. Ол қазынада 150 қалдырды. Әуелде қазынада қанша болғанын білгіміз келеді?»
- ін екінші біреу алды. Ол қазынада 150 қалдырды. Әуелде қазынада қанша болғанын білгіміз келеді?»
Барлығы - х
І -
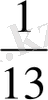 х
х
ІІ -
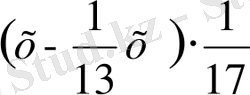
Қалды - 150
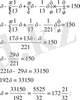
№10. Диофанттың қабіріндегі құлпытаста былай деп жазылған: «Диофанттың балалық шағы - өмірінің алтыдан бірі, жастық шағы - он екіден бірі, ал баласыз өткен ерлі-зайыпты өмірінің жетіден бірі және тағы 5 жыл өткенде
ұлды болды. Әкесінің жарты жасына келгенде ұлы дүние салды, бұдан кейін Диофант тек 4 жыл ғана өмір сүрді. Диофант неше жыл сүрген еді?»
Өмірі - х
Балалық шағы -
 х
х
Баласыз -
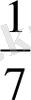 х
х
Жастық шағы -
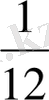 х
х
Ұлды -
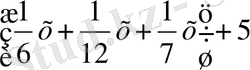 ;
;
Ұлы дүние салды -
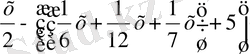 ;
;
Өзі дүние салды -
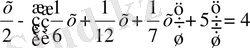 ;
;

Жауабы: Диофант 84 жыл өмір сүрді.
№11. «Көпестің жинақтаған азды-көпті ақшасы бар еді. Ол жыл сайын семьясының қажетіне 100 фунт ақша ұстап, қалған ақшасына оның үштен біріндей ақша қосып отыратын. Үш жыл өткеннен кейін ол қаражатының екі есе көбейгендігін байқады. Әуелде оның қанша ақшасы болған еді?»
Бар еді - х
Бір жылдан соң қолында қалды - х - 100
Үш жылдан соң болды -
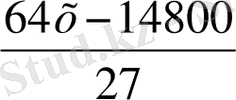 ;
;
Жинақталған ақшасы әуелгі ақшасынан екі есе артық болды.
Шешуі:
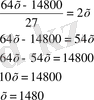
Жауабы: Әуелдегі ақшасы 1480 фунт.
№12. «Бақташы 70 өгіз айдап келеді. Оған мынадай сұрақ берілген: Үлкен табынының бұл айдап келе жатқаның қанша?
Бақташы жауабы:
− Табындағы барлық малдың үштен бірінің үштен екісі.
Есептеп көр!»
(Бүкіл табында қанша өгіз болғандығын білу керек. )
Шешуі:
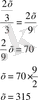
Жауабы: Бүкіл табында
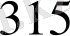 өгіз болған.
өгіз болған.
№13.
Ежелгі римдік есеп. ІІ ғ.
«Бір адам өлерінде былай деп өсиет қалдырған: егер әйелім ұл тапса, онда оған имениемнің
 - сі, ал әйеліме қалған бөлігі берілсін. Егер қыз туса, онда оған
- сі, ал әйеліме қалған бөлігі берілсін. Егер қыз туса, онда оған
 - і, ал әйеліме
- і, ал әйеліме
 - сі берілсін. Егіз бала - қыз және ұл туды. Имение қалай бөлінуі керек?»
- сі берілсін. Егіз бала - қыз және ұл туды. Имение қалай бөлінуі керек?»
Жауабы: Ұлы әйелінен екі есе көп үлесін, әйелі - қызынан екі есе көп үлесін алуы тиіс. Имениені ұлы, әйелі және қызына 4:2:1 сандарына тура пропорционал етіп бөліп берген жөн.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz