Stud.kz

Механикалық қозғалыс. Кинематика


Пән: Физика
Жұмыс түрі:  Дипломдық жұмыс
Тегін:  Антиплагиат
Көлемі: 152 бет
Таңдаулыға:   

Механика

§1. Механикалық қозғалыс

Материялық дүниеде болатын кез келген өзгерісті, материялық денелердің кез келген өзара әрекетін қозғалыс деп атайды. Материяның ең қарапайым қозғалыс формасы - механикалық, қозғалыс. Механикалық қозғалыс деп дененің басқа денелермен салыстырғаңдағы орын ауыстыруын атайды.

Кинематика

Дене қозғалысының өзгеру себептерін есепке алмай, қозғалысты қарастыратын механика бөлімі кинематика деп аталады.

Материялық нүкте

Егер қозғалған дененің өлшемі оның жүрген жолынан көп кем болса, онда дене қозғалысын нүктенің қозғалысы ретінде қарастыруға болады.

Мұндай жағдайларда қозғалған денені материялық нүкте деп атайды.

Қозғалыс траекториясы. Жол

Қозғалған материялық нүктенің кеңістіктегі болған нүктелер жиынтығын құрастыратын сызықты траектория : деп атайды. Траектория ұзындығы S жол деп аталады.

Орын ауыстыру

Траекторияның бастапқы және соңғы нүктелерін қосатын вектор

\[\begin{array}{l}{{\frac{1}{1}}}\\ {{\binom{1}{3}}}\end{array}\]
- орын ауыстыру векторы. Түзу сызықты қозғалыс болғанда, жол S орын ауыстыру векторының
\[\left|{\frac{1}{N}}\right|\]
модуліне тең.

Қисық сызықты қозғалыста орын ауыстырудың модулі

\[\left|{\frac{1}{N}}\right|\]
жүрген S жолдан кем (2. 1-сурет) .

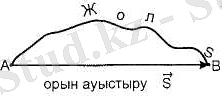
2. 1-сурет

Материялық нүктенің қозғалысын сипаттау үшін, уақыттың әрбір мезетінде оның кеңістіктегі орны көрсетілуі керек.

Координаталар. Санақ денесі.

Координаталар жүйесі

Нүктенің кеңістіктегі орны оның координаталарымен анықталады. Нүктенің координаталарын анықтау үшін алдымен санақ денесі таңдап алынады, одан кейін осы денемен координаталар жүйесін байланыстырады.

Санақ жүйесі

Санақ денесі, онымен байланысқан координаталар жүйесі және бастапқы мезеті көрсетілген уақыт санауы санақ жүйесін кұрастырады.

Механикалық қозғалыстың салыстырмалылығы

Қозғалыс траекториясы, жүрілген жол және орын ауыстыру санақ жүйе тандалуына тәуелді. Басқаша айтқанда, механикалық қозғалыс - салыстырмалы ұғым.

Мысалы, Күннің орны қайда және ол қалайша қозғалады деген сұраққа әр түрлі жауаптар беруге болады.

Егер санақ жүйесін алыс галактикалармен байланыстырсақ (2. 2-сурет), Күн біздің Құс жолы галактиканың орталығын 3 • 10 20 м қашықтықта 250 км/с жылдамдықпен 200 миллион жылда бір рет айналады.

2. 2-сурет

Санақ денесі ретінде Жерді таңдап алып, координаталар жүйесінің бастапқы нүктесін Жер бетінде орналастырайық. Бұл санақ жүйесінде Күн орталығы Жерде орналасқан радиусы 150 миллион километр шеңберді 1 км/с жылдамдықпен тәулігіне бір рет айналады.

Соңында Күнді санақ денесі ретінде таңдап алып, өзімен координаталар жүйесін байланыстырайық. Бұл санақ жүйесінде Күн қозғалмайды, ал Жер оны радиусы 150 миллион километр шеңбер бойымен 30 км/с жылдамдықпен айналады (2. 3-сурет) .

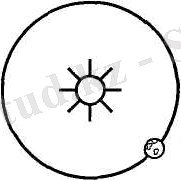
2. 3-сурет

Күннің қозғалысы туралы берілген үш жауаптың қайсысы дұрыс? Дене қозғалысының кинематикалық суреттемесін беру үшін, барлық санақ жүйелерін тең түрде қабылдауға болады және әрбір суреттеменің нәтижелері тиісті санақ жүйелерінде дұрыс деу керек.

Координаталар, орын ауыстыру, қозғалыс траекториясы, жылдамдық- салыстырмалы ұғымдар. Денелердің абсолют координаталары, жылдамдықтары болмайды, олар санақ денесін, санақ жүйесін тандаумен байланысты.

Механикалық қозғалыс - салыстырмалы ұғым.

§2. Жылдамдық

Көп жағдайда дененің кез келген уақыт мезетінде қай жерде орналасуымен қатар, ол қалайша қозғалатынын білу қажет. Қозғалыс процесінің сандық сипаттамасы ретінде қозғалыс жылдамдығы деген ұғым енгізіледі.

Бір қалыпты қозғалыс және оның жылдамдығы

Егер қозғалған дене әрбір бірдей уақыт аралығында бірдей жол жүрсе, бұл қозғалысты бір қалыпты қозғалыс деп атайды. Бір қалыпты қозғалыс болғанда, жүрген S жолдың t уақыт аралығына қатынасы тұрақты шама болады. Бұл қатынас бір қалыпты қозғалыстың жылдамдығы деп аталады.

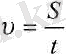(2. 1) .

Дененің бастапқы уақыт t = 0 мезетіндегі кеңістіктегі орны, қозғалыс траекториясы және V жылдамдығы белгілі болса, онда бір қалыпты қозғалған дененің басқа да кез келген уақыт мезетіндегі координаталарын білуге болады. Дененің жылдамдығын жүрген уақытына көбейтсек, жүрген жолы S табылады:

S= v ∙ t (2. 2) .

Бастапқы А нүктеден траектория бойымен жүрген S жолды санап, нүктенің жаңа t уақыт мезетіндегі В нүктедегі орнын анықтаймыз.

Мысалы, тұрақты v жылдамдықпен қозғалған автомобиль тандап алған ABC маршрутпен t уақыт жүргенде, қай жерге жететінін картаны пайдаланып анықтауға болады (2. 4-сурет) .

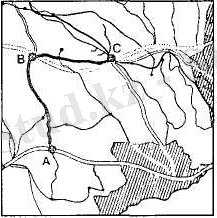
2. 4-сурет

Егер дене түзу сызықпен бір қалыпты қозғалса, онда координата өсін қозғалыс бағытымен сәйкестендіріп, дененің кеңістіктегі орнын бір мәнді түрде, бір ғана координата анықтайтындай жағдай туындайды. Онда t yaқыт аралықтағы координатаның өзгерісі

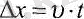(2. 3),

ал әлдебір t уақыт мезетіндегі координата х:

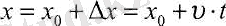(2. 4),

тендеу арқылы табылады. Мұндағы х 0 - бастапқы t= 0 уақыт мезетіндегі дененің бастапқы координатасы (2. 5-сурет) .

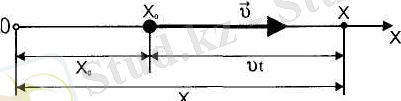
2. 5-сурет

Erep Ox ось бағыты қозғалыс бағытына кері болса (2. 6-сурет) онда t мезетте х координатасы:

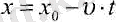(2. 5),

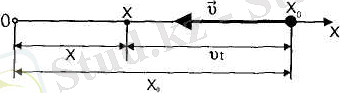
2. 6 - сурет

Бір қалыпты қозғалған дененің қозғалыс графигі

Төмендегі 2. 7-суретте бір қалыпты

\[\mathcal{U}\]
жылдамдықпен қозғалған дененің X координатасы t уақыттан қалайша тәуелді екенін көрсететін сызықтар бейнеленген.

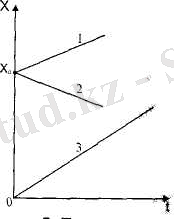
2. 7 - сурет.

График 1. Бастапқы координатасы х 0 , нүкте

\[\mathcal{U}\]
жылдамдықпен х осі бойымен қозғалады.

График 2. Бастапқы координатасы х 0 , дене координата осіне қарсы бағытта қозғалады.

График 3. Бастапқы координатасы х 0 = 0, дене координата осі бағыты бойымен қозғалады.

Бір қалыпты емес қозғалыс

Нақты жағдайларда денелердің қозғалысы ешқашан дәлме-дәл бір қалыпты болмайды. Дене бірдей уақыт аралықтарында әр түрлі жол ететін болған қозғалысты бір қалыпты емес қозғалыс деп атайды.

Бір қалыпты емес қозғалыс жолдық

\[v_{\mathrm{\Large~id}}\]
орташа жылдамдығымен және лездік
\[\overset{\mathbb{N}}{U}\]
жылдамдығымен сипатталады.

Орташа жылдамдық

Дененің S жүрген жолының осы жолды жүрген t уақыт аралығына қатынасын орташа жолдық жылдамдық деп атайды.

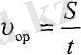(2. 6) .

S жол және t уақыт - скалярлық шамалар, сондықтан орташа жылдамдық

\[v_{\mathrm{\Large~id}}\]
- скалярлық шама.

Лездік жылдамдық

Материялық нүктенің t уақыт мезеті маңайында аз ғана

\[\Delta_{S}^{1}\]
уақыт аралығында болған As орын ауыстырудың осы (
\[\Lambda_{\bf d}\]
t >0) уақыт аралығына қатынасын лездік жылдамдық деп атайды.

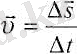( 2. 7) .

Орын ауыстыру

\[\Delta_{S}^{1}\]
- векторлық шама, уақыт аралығы
\[\Lambda_{\bf d}\]
t -скаляр, сондықтан лездік жылдамдық
\[\overset{\mathfrak{g}}{U}\]
-векторлық шама.

Лездік жылдамдық векторының бағыты

Барлық жағдайда лездік жылдамдық векторы

\[\overset{\mathfrak{g}}{U}\]
қозғалыс траекториясына жанама бағытта болады. Егер t уақыт мезетінде денеге әрекет ететін күштер түгелдей жойылып кететін болса, дене осы V бағытта қозғалысын жалғастырады (2. 8-сурет) .

2. 8-сурет

Жылдамдықтың өлшем бірлігі

Халықаралық жүйеде қашықтықтың өлшем бірлігі - метр, уақыттың өлшем бірлігі - секунд, сондықтан жылдамдықтың өлшем бірлігі - секундына метр:

1 м/с = 1м/1с.

Жылдамдықтың және бір қалыпты қозғалыс жолының графиктері

Бір қалыпты қозғалыс болғанда,

\[\overset{\mathfrak{g}}{U}\]
жылдамдықтың t уақыттан тәуелділік графигінде жылдамдық сызығы - t уақыт белгіленген абсцисса осіне параллель түзу (2. 9-сурет) .

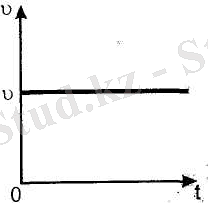
2. 9-сурет

Бір қалыпты қозғалыс болғанда, S жылдамдықтың t уақыттан тәуелділігін бастапқы нүктеден өтетін түзу бейнелейді (2. 10-сурет) . Бұл графикте S ординатасының t абсциссаға қатынасы

\[\mathcal{U}\]
жылдамдықты анықтайды.

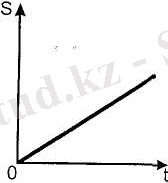
2. 10-сурет

§3. Үдеу

Егер уақыт өте қозғалған дененің лездік жылдамдығының модулі немесе бағыты өзгеретін болса, онда дененің қозғалысын толық сипаттау үшін дененің жылдамдығы уақыт бойынша қалай өзгеретінін білу қажет.

Үдеу

Физикада дене жылдамдығының өзгерісін сипаттау үшін үдеу ұғымын енгізеді.

Өте аз (

\[\Lambda_{\bf d}\]
t → 0 ) уақыт аралығында болған жылдамдық
\[\Delta{\dot{v}}\]
өзгерісінің осы уақыт аралығына қатынасын үдеу деп атайды.

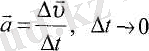(3. 1) .

Үдеу - векторлық шама. Үдеудің өлшем бірлігі -м/с 2 (3. 1) :

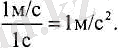
Түзу сызықты қозғалған дененің жылдамдығы өскенде, жылдамдық өсімшесінің

\[\textstyle\bigcap_{}^{}{\cal\Lambda}\arg\stackrel{\parallel}{\longrightarrow}\overbrace{}^{}\xrightarrow{}\]
бағыты (
\[\overset{\sharp}{\mathcal{U}}\]
2 >
\[\overset{\sharp}{\mathcal{U}}\]
1 болғандықтан)
\[\overset{\sharp}{\mathcal{U}}\]
2 жылдамдық бағытымен бірдей. Сондықтан бұл жағдайда
\[\stackrel{1}{Q}\]
үдеу және
\[\overset{\sharp}{\mathcal{U}}\]
2 бағыттары бірдей.

Егер түзу сызықты қозғалған дененің жылдамдығы кемісе (

\[\overset{\sharp}{\mathcal{U}}\]
2 <
\[\overset{\sharp}{\mathcal{U}}\]
1 ), онда
\[\Delta{}^{*}\]
жылдамдық бағытына қарама-қарсы бағытталған,
\[\stackrel{1}{Q}\]
үдеу бағыты
\[\overset{\sharp}{\mathcal{U}}\]
1 жылдамдық бағытына кері бағытталады.

Қисық сызықты қозғалыс болғанда, үдеу

\[\frac{1}{Q}\]
векторы жыkдамдық векторымен әр түрлі бұрыш құрастырады.

Бір қалыпты үдемелі қозғалыс

Үдеудің модулі және бағыты өзгермейтін қозғалыс бір қалыпты үдемелі деп аталады.

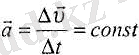(3. 2) .

§4. Бір қалыпты үдемелі түзу сызықты қозғалыс

Әрбір бір қалыпты үдемелі қозғалысты тиісті санақ жүйесін таңдау арқылы бір қалыпты үдемелі түзу сызықты қозғалыс ретінде қарастыруға болады.

Мысалы, h биіктіктен

\[\overset{\mathfrak{g}}{U}\]
жылдамдықпен горизонталь бағытта лақтырылған дене Жермен байланысты санақ жүйесінде парабола бойымен бір қалыпты үдемелі қозғалады және оның
\[\overset{\mathfrak{g}}{U}\]
жылдамдығының модулі де, бағыты да өзгереді (2. 11-сурет) .

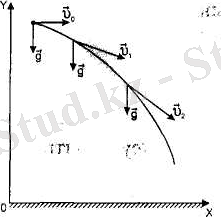
2. 11-сурет

Егер қозғалысты Жермен салыстырғанд

\[\overset{\mathfrak{g}}{U}\]
0 жылдамдықпен қозғалған санақ жүйесінде қарастырсақ, бағанағы дене бір қалыпты үдемелі түзу сызықты қозғалыста болады (2. 12-сурет) .

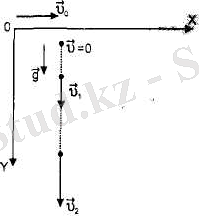
2. 12-сурет

Бір қалыпты үдемелі түзу сызықты қозғалыстың жылдамдығы

Бір қалыпты үдеумен (

\[\stackrel{1}{Q}\]
=const ) қозғалған дене түзу бойымен қозғалғанда

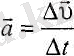(4. 1),

қатынас тек қана өте аз уақыт аралықтары емес, қандай да уақыт аралықтары үшін де орындалады. Бір қалыпты үдемелі түзу сызықты қозғалыс үшін жылдамдық

\[\overset{\mathfrak{g}}{U}\]
және
\[\stackrel{1}{Q}\]
үдеу арасындағы байланысты анықтайық.

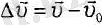(4. 2),

және

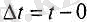(4. 3),

онда (4. 1), (4. 2), (4. 3) -тен

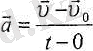(4. 4),

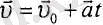(4. 5),

Үдемелі түзу сызықты қозғалыста

\[\overset{\mathfrak{g}}{U}\]
және
\[\overset{\mathfrak{g}}{U}\]
0 бағыттары бірдей немесе өзара қарама-қарсы болуы мүмкін.
\[\overset{\mathfrak{g}}{U}\]
0 және
\[\stackrel{1}{Q}\]
бағыттары бірдей болса
\[\overset{\mathfrak{g}}{U}\]
:

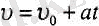(4. 6),

формула бойынша саналады.

Егер

\[\stackrel{1}{Q}\]
үдеу
\[\overset{\mathfrak{g}}{U}\]
0 векторына кері бағытталса:

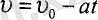(4. 7),

формула арқылы есептеледі. Бұл жағдайда 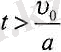уақыт мезеттерінде

\[\overset{\mathfrak{g}}{\mathcal{O}}\]
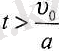0 жылдамдығының таңбасы теріс. Мағынасы былай: асқан уақытта
\[\overset{\mathfrak{g}}{U}\]
жылдамдық бағыты бастапқы
\[\overset{\mathfrak{g}}{U}\]
0 жылдамдық бағытына қарсы болады.

Егер бастапқы жылдамдық

\[\overset{\mathfrak{g}}{U}\]
0 = 0 болса, онда

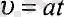(4 8),

Бір қалыпты үдемелі түзу сызықты қозғалыс жылдамдығының графигі

Бастапқы жылдамдығы жоқ (

\[\overset{\mathfrak{g}}{U}\]
0 = 0) бір қалыпты үдемелі түзу сызықты қозғалыс
\[\overset{\mathfrak{g}}{U}\]
жылдамдығының t уақыттан тәуелділігі 2. 13-суретте бейнеленген.

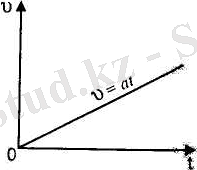
2. 13-сурет

Егер бастапқы жылдамдығы

\[\overset{\mathfrak{g}}{U}\]
0
\[\frac{\overline{{n}}}{\overline{{r}}}\]
0 болса, бір қалыпты үдемелі түзу сызықты қозғалыс
\[\mathcal{U}\]
жылдамдығының t yaқыттан тәуелділігі 2. 14-суретте көрсетілген.

Екі жағдай:

а)

\[\overset{\mathfrak{g}}{U}\]
0 ,
\[\frac{1}{Q}\]
бағыттары бірдей (үдемелі) ;

ә)

\[\overset{\mathfrak{g}}{U}\]
0 ,
\[\frac{1}{Q}\]
бағыттары қарама-қарсы (кешмелі) .

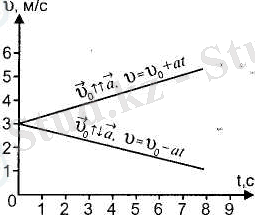
2. 14-сурет

Бір қалыпты емес үдемелі қозғалыстың мысалы ретінде денелердің Жерге құлау қозғалысын келтіруге болады. Тәжірибелердің көрсетуінше, ауада құлаған денелердің қозғалысы бір қалыпты үдемелі емес, әр түрлі денелердің жылдамдығы уақыт бойынша әр түрлі өзгереді.

Қорғасынның кесегін, тығынды, қауырсынды ауа толтырылған шыны түтікке орналастырып тез төңкерсек, олар түтіктің түбіне әр уақытта, алдымен қорғасынның кесегі, одан кейін тығын және көп кешігіп қауырсын, жетеді.

Егерде түтіктегі ауаны алдын ала сорғымен сорып алсақ, онда вакуумда үш дене де түтік түбіне бірге жетеді (2. 15-сурет) .

2. 15-сурет

Еркін түсу

Бос кеңістікте (вакуумда) түсу еркін түсу деп аталады.

Еркін түсу үдеуі

Еркін құлаған денелердің үдеулері бірдей. Бос кеңістікте Жерге құлаған денелердің үдеуі еркін түсу үдеуі деп аталады. Оны g әрпімен белгілейді.

Еркін түсу үдеуін Жер бетінің әр түрлі нүктелерінде жуықтап санағанда бірдей деуге болады g

\[\lesssim\]
9, 8 м/с 2 .

Егер есептеулерде үлкен дәлдік қажет болмаса, Жер бетіндегі еркін түсу үдеуін 10 м/с 2 деп алады.

§5. Бір қалыпты үдемелі түзу сызықты қозғалыста болған дененің жүрген жолы

Бір қалыпты айнымалы түзу сызықты қозғалыс практикада жиі кездеседі. Мысалы, тыныштық қалпынан қозғала бастаған пойыз, автокөлік, ұшақ қозғалыстарын әжептәуір дәлдікпен осындай қозғалысқа жатқызуға болады.

Жылдамдық графигінен жүрген жолды анықтау

Бір қадыпты қозғалған дененің

\[\mathcal{U}\]
жылдамдығының t уақыттан тәуелділік графигі абсцисса осіне параллель сызық болады (2. 1 б-сурет) .

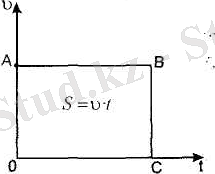
2. 16-сурет

Бір қальшты қозғалған дененің жүрген жолы ОАВС тікбұрыш ауданына тең:

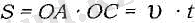(5. 1)

және бұл (2. 2) теңдеуге сәйкес.

Бір қалыпты үдемелі түзу сызықты қозғалыста болған дененің

\[\mathcal{U}\]
жылдамдығының t уақыттан тәуелділігі (2. 17-сурет) АВ түзуі арқылы бейнеленеді. Аз ғана
\[\Lambda_{\bf d}\]
t аралығында дененің жүрген жолы табаны
\[\Lambda_{\bf d}\]
t кішігірім тікбұрыштың ауданына тең. Осындай тікбұрыштардың ауданын қоссақ, ол OABD трапецияның ауданына тең болады. Сонымен жылдамдық графигіндегі жылдамдық сызығының астындағы аудан дененің жүрген жолын анықтайды (2. 17-сурет) .

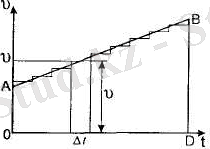
2. 17-сурет

ОАВD трапецияның ауданы OACD тікбұрыштың және ABC үшбұрыштьщ аудандарының қосындысына тең (2. 18-сурет) :

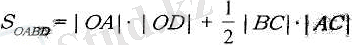
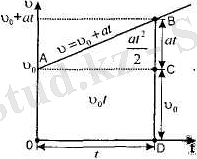
2. 18-сурет

Сонымен t - уақыттадененің жүрген S жолы анықталады:

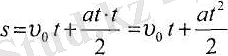(5. 2),

Егер бір қалыпты кемімелі түзу сызықты қозғалыста

\[\mathcal{U}\]
, а бағыттары қарама-қарсы болса, жол
\[\mathcal{U}\]
жылдамдығының t уақыттан тәуелділік графигінен анықталады (2. 19-сурет) .

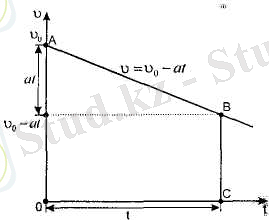
2. 19-сурет

Онда жүрген жол ОАВС трапецияның ауданына тең:

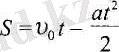(5. 3) .

Бастапқы жылдамдығы нөлге тең бір қалыпты үдемелі түзу сызықты қозғалыс болғанда жод жылдамдық және үдеу арасындағы байланыс

Егер

\[\mathcal{U}\]
0 = 0 болса, (5. 2) формуладан

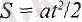(5. 4) .

Ал (5. 4) және (4. 8) формулалардан:

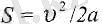(5. 5) .

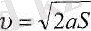(5. 6) .

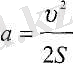(5. 7) .

және (5. 4) формуладан

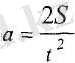(5. 8) .

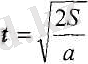
§6. Дененің шеңбер бойымен бір қалыпты қозғалысы

Дененің шеңбер бойымен модулі тұрақты жылдамдықпен қозғалуын табиғатта және техникада жиі кездестіруге болады. Мысалы, Айдың Жерді, Жердің Күнді айналуын әлдебір дәлдікпен осы қозғалыс түріне жатқызуға болады.

Материялық нүкте шеңбер бойымен бір қалыпты қозғалғанда,

\[\overset{\mathfrak{g}}{U}\]
жылдамдық векторының бағыты үздіксіз өзгеріп отырады, бірақта оның модулі тұрақты болады. Жылдамдық векторының бағыты уақыт өте өзгеретін болғандықтан, бір қалыпты шеңберлі қозғалыс үдемелі қозғалыс болады.

Центрге тартқыш үдеу

Жылдамдық векторының модулі уақыттан тәуелсіз болғандықган, әрбір уақыт мезетінде үдеу векгоры

\[\frac{1}{Q}\]
жылдамдық
\[\overset{\mathfrak{g}}{U}\]
векторына перпендикуляр болады, үдеудің жылдамдық бағытына құраушысы жоқ (2. 20-сурет) . Дене шеңбер бойымен бір қалыпты қозғалғанда, оның үдеуі уақыттың әрбір мезетінде шеңбердің центріне бағытталады, соңдықтан оны центрге тартқыш үдеу деп атайды.

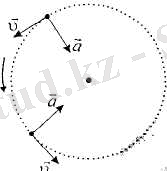
2. 20-сурет

Центрге тартқыш үдеудің модулін анықтайық. Ол үшін жылдамдық векторы модулі AV өзгерісінің осы өзгеріс болған кішігірім

\[\Lambda_{\bf d}\]
t уақыт аралығына қатынасын іздестірейік (2. 21-сурет) . Уақыт аралығы
\[\Lambda_{\bf d}\]
t өте аз болғандықтан, шеңбердің А және В нүктелеріндегі
\[\overset{\mathfrak{g}}{U}\]
және
\[\overset{\mathfrak{g}}{U}\]
B жылдамдықтар векторлары арасындағы бұрыш та өте кішкентай, сондықтан

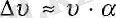(6. 1) .

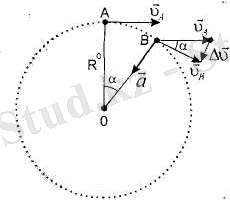
2. 21-сурет

А және В нүктелердегі жылдамдық векторлары арасындағы бұрыш А және В нүктелерді шеңбердің центрімен қосатын радиустар арасындағы

\[{\mathcal{Q}}\]
бұрышка тең:

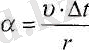(6. 2) .

(6. 1) және (6. 2) формулаларын пайдаланып, бір қалыпты шеңберлі қозғалыстың центрге тартқыш үдеуін анықтаймыз:

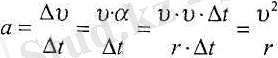(6. 3) .

Дене шеңбер бойымен бір қалыпты қозғалғанда, оның центрге тартқыш үдеуінің модулі өзгермейді, ал үдеудің бағыты үздіксіз өзгереді. Сондықтан бір қалыпты шеңберлі қозғалыс бір қалыпты айнымалы қозғалыс емес, оның үдеуі үздіксіз бағытын өзгертеді.

Период және жиілік

Дененің шеңберді бір рет айналып ететін уақыт аралығын айналу периоды деп атайды және Т әрпімен белгілейді. Радиусы r шеңберде

\[\mathcal{U}\]
жылдамдықпен бір қалыпты қозғалған дененің Т айналу периодын анықтау үшін, шеңбердің ұзындығын жылдамдыққа бөлеміз:

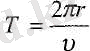(6. 4) .

Периодқа кері шама айналу жиілігі деп аталады және

\[\mathcal{O}\]
әрпімен белгіленеді:

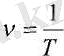(6. 5) .

(6. 3), (6. 4), (6. 5) формулалардан

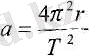(6. 6) .

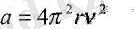(6. 7) .

§7. Жылдамдықтардың қосылуы

Жылдамдықтардың классикалық қосылу заңы

Дене қозғалысының траекториясы, жолы және жылдамдығы - салыстырмалы шамалар, олар санақ жүйесін таңдауға тәуелді. Біраз практикалық есептерде бір дененің әр түрлі санақ жүйелеріндегі жылдамдықтарының байланысын білу қажет.

Егер дене бірінші санақ жүйесінде

\[\overset{\mathfrak{g}}{U}\]
жылдамдықпен қозғалса және бірінші санақ жүйесі екіншісімен салыстырғанда
\[\overset{\mathfrak{g}}{U}\]
1 жылдамдықпен қозғалса, онда тәжірибеде анықталғандай, дененің екінші санақ жүйесіндегі
\[\mathcal{U}\]
жылдамдығы
\[\overset{\mathfrak{g}}{U}\]
1 және
\[\overset{\mathfrak{g}}{U}\]
2 жылдамдықтардың қосындысына тең:

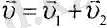(7. 1) .

Бұл заң жылдамдықтардың классикалық қосылу заңы деп аталады. Мысалы, Жермен салыстырғанда

\[\overset{\mathfrak{g}}{U}\]
1 жылдамдықпен аққан өзен суының бетінде сумен салыстырғанда
\[\overset{\mathfrak{g}}{U}\]
2 жыддамдықпен қозғалған қайықтың Жермен салыстырған жылдамдығы
\[\overset{\mathfrak{g}}{U}\]
,
\[\overset{\mathfrak{g}}{U}\]
1 және
\[\overset{\mathfrak{g}}{U}\]
2 жылдамдықтардың векторлық қосындысына тең (2. 22-сурет) .

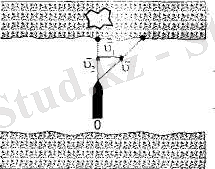
2. 22-сурет

Ал дененің үдеуі, жылдамдықтан айрықша, өзара тұрақты жылдамдықпен қозғалған барлық санақ жүйелерінде бірдей болады.

Жылдамдықтардың классикалық қосылу заңын пайдалануының шектелуі

Жылдамдыктардың классикалық қосылу заңын қолдану ауқымы шектелген. Бұл заң с

\[\iff\]
3 км/с вакуумдағы жарық жылдамдығынан көп кем болатын
\[\overset{\mathfrak{g}}{U}\]
1 және
\[\overset{\mathfrak{g}}{U}\]
2 жылдамдықтар үшін үлкен дәлдікпен орындалады. Ал дененің
\[\overset{\mathfrak{g}}{U}\]
2 немесе санақ жүйесінің
\[\overset{\mathfrak{g}}{U}\]
1 жылдамдықтары вакуумдағы с жарық жылдамдығына жақындағанда, жылдамдықтар релятивтік қосылу ережесіне бағынады (54. 1) .

Автокөлік, пойыз, ұшақ және ғарыш зымыраны, планеталар және жасанды Жер серіктерінің Жермен салыстырған жылдамдықтары жарық жылдамдығынан кем. Сондықтан олардың қозғалыстарын Жермен байланысты немесе Жермен салыстырғанда,

\[\mathcal{U}\]
<< с жылдамдықпен қозғалатын санақ жүйелерінде қарастырғанда, жылдамдықтардың классикалық қосылу заңын пайдалануға болады.

§8. Ньютонның бірінші заңы Динамика

Егер дененің жылдамдығы және үдеуі уақыт өте қалай өзгеретіні белгілі болса, кинематика заңдарын пайдалану негізінде дене қозғалысын толық суреттеуге болады. Егер үдеудің уақыт бойынша өзгеру заңы белгілі болса, онда жылдамдықтың уақыттан тәуелділігі анықталады. Алайда, дененің үдеуін тек қана басқа денелермен өзара әрекетін қарастыру арқылы ғана анықтауға болады.

Денелердің өзара әрекетін зерттейтін механика бөлімін динамика деп атайды.

Төңірегіміздегі денелер қозғалысын байқасақ, көбінесе денелер қозғалыста болу үшін оларға баска денелер әсер етіп отыру керек. Автокөлік моторын сөндірсе, аз уақыттан соң тоқтайды, допты соқса, ол да біраз домалап, тоқтайды.

Бірақ итальян ғалымы Галилео Галилей денелер қозғалысын байқаудан принципті жаңа тұжырым жасады. Ол қозғалған денелер жылдамдықтарының өзгерісі әр түрлі жағдайда түрліше өзгеретініне көңіл аударды. Бірдей бастапқы жылдамдығы бар тас, құммен салыстырғанда, мұз бетінде тоқтағанша көбірек сырғанайды. Осындай байқаулар нәтижесінде Галилей мынадай тұжырымға келді: әрбір дененің жылдамдығы тек қана басқа денелермен өзара әрекеті нәтижесінде ғана өзгереді.

Инерция заңы

1632 жылы Галилей инерция заңын тұжырымдады: егер денеге басқа денелер әсер етпесе, немесе олардың әсерлері бір-бірін теңестірсе, онда денетыныштық күйін, немесе бір қалыпты түзу сызықты қозғалыс күйін, сақтайды.

Ньютонның бірінші заңы

Ұлы ағылшын ғалымы Исаак Ньютон инерция заңын механиканың негізгі заңдарының қатарына енгізді, сондықтан инерция заңын Ньютонның бірінші заңы, немесе механиканың бірінші заңы, деп атайды.

Инерция

... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
Кинематиканың негізгі түсініктері
Материялық нүкте кинематикасының және жалпы кинематика есептерін шешуге қысқаша әдістемелік нұсқаулар
Кинематика мен динамика заңдарын оқыту әдістемесі
Материалдық нүктенің үдеуі
МЕХАНИКА
Кинематика бөлімін оқыту әдістемесі
Деңгейлеп саралап оқыту технологиясын қолданудың тиімділігі
Теориялық механиканың кинематика бөлімі
Инерция күштері
Физика міндеті
Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

google play appstore

instagram tiktok

Ақпарат

Қосымша


Email: info@stud.kz



Реферат Курстық жұмыс Диплом Материал Диссертация Практика Презентация Сабақ жоспары Мақал-мәтелдер 1‑10 бет 11‑20 бет 21‑30 бет 31‑60 бет 61+ бет Негізгі Бет саны Қосымша Іздеу Ештеңе табылмады :( Соңғы қаралған жұмыстар Қаралған жұмыстар табылмады Тапсырыс Антиплагиат Қаралған жұмыстар kz