Корреляциялық және регрессиялық анализ: ең аз квадраттар әдісі және үрдістерді модельдеу


Мазмұны
Кіріспе . . . 2
I-Тарау. Корреляциялық және регрессиялық анализ . . . 3
1. 1. Функционалдық және корреляциялық тәуеділіктер . . . 3
1. 2. Корреляциялық таблица және регрессия теңдеуі . . . 5
1. 3. Ең аз квадраттары әдісі . . . 9
1. 4. Жиі пайданылатын функциялар мен олардың қалыпты теңдеулері . . .
. . . 12
1. 5. Корреляция коэффициенті . . . 13
1. 6. Кез келген түдегі керреляциялық байланыс . . . 16
1. 7. Корреляциялық коэффициент сенімділігі. Корреляциялық қатынас. .
. . . 18
1. 8. Көп шамалар арасындағы корреляциялық байланыс. Барлық
корреляция . . . 18
1. 9. Рангтік белгілер үшін корреляция коэффициенттері . . . 22
1. 10. Спирменнің рангтік корреляция коэффициенті . . . 22
II-тарау. Үрдістердің базасын модельдеу әдісімен алдын ала болжам жасап зерттеу . . . 24
Қорытынды . . . 58
Пайдаланған әдебиеттер . . . 59
Қосымша . . . 61
Кіріспе
Ғасырымыздың ең маңызды жаңалықтарының бірі болып табылатын компьютер күнделікті өміріміздің әрбір саласына ене бастады. Компьютер алғашқы кезде тек белгілі бір мақсаттарға ғана қолданылды. Уақыт өте келе көлемі кішірейіп құны да арзандады. Соның нәтижесінде түрлі салаларда кеңінен қолданыла бастады.
Ғылыми ақпараттың құрылымы мен жалпы қасиеттерін, сондай-ақ оны іздеп табу, жинау, сақтау, өңдеу, түрлендіру, тарату және қолдану мәселелерін зерттейтін информатиканың ғылым болып қалыптасуы және адам іс-әрекетінің барлық салаларында компьютердің (электрондық есептеуіш техниканың) қолданылуы өткен ғасырдың елуінші жылдарына түтас келді. Одан бергі кезеңде информатика дербес ғылым саласы болып кемелденіп, компьютер технологиялық көліктік, энергетикалық және басқа да өндірістік процесстерді басқаруда. Күрделі объектілерді жобалауда, жосларлау, статистика, үйымдастыру-әкімшілік басқару, оқыту, ғылыми зерттеулер жүргізу салаларында, әсіресе информатикада кеңінен қолданылатын болды. Ғылыми техникалық прогрестің қарқынын жеделдетуде жөне түптеп келгенде, қоғамдық өндірістің нәтижелілігін кеңейтуде бұл салалардың маңызы барған сайын арта тусіп отыр. Өркениет өріне бет түзеп, озық елдермен теңесуге күш салып жатқан біздің елімізде де бұл салаларға мемлекеттік тұрғыдан барынша көңіл бөлініп, ауқымды шаралар атқарылуда. Осыған байланысты. жаңа программалардың тасқыны, көптеген адамдарға кәсіптік-ақпараттық технология құралдарын жоғары дәрежеде білу қажеттігін көрсетеді.
I-Тарау. ҚОРРЕЛЯЦИЯЛЫҚ ЖӘНЕ РЕГРЕССИЯЛЫҚ АНАЛИЗ
1. 1. Функционалдық және корреляциялық тәуеділіктер
Шамалар арасындағы функционалдық тәуелділіктер туралы сөз еттік. Одан шамалардың біреуінің әрбәр мәніне екіншісінің белгілі бір мәні (функция бірмәнді) немесе бірнеше мәндері (функция көпмәнді) сәйкес келуі мүмкін. Ал іс жүзінде мұндай анық бола бермейді. Мысалы, мақта өнімін (шаманы) қарастырсақ, онда бұл өнімге түрлі факторл ар әсер етеді. Бұл факторларға тыңайтқыш мөлшері, жауын - шашын, күн сәулесі, түсетін күндер саны т. т. жатады. Мұндай бір шаманың бір мәніне екінші шаманың бірнеше мәндері сәйкес келгенімен, яғни бір шаманы екіншісіне тәуелділігі байқалғанымен, ол шамалар саны да және қабылдайтын мәндері де толық, анық еместігін байқаймыз.
Біртектес жиынды оның кез - келген белгісі бойынша немесе бірнеше белгілерінің байланысы бойынша қарастыруымызға болады. Тек осылайша қарастыру нәтижесінде процесс немесе құбылыс заңдылығын, яғни процесс не құбылысты сипаттайтын әр түрлі шамалар арасындағы байланысты математикалық абстракциялау мүмкін. Сондықтан математикалық әдістерді қолданатын зертеушілердің алдына қоятын бірден бір міндет сол математикалық абстракциялау формула күйнде немесе таблица күйінде, немесе график түрінде беріледі.
Математикалық екі шама немесе айнымалылар арасындағы тәуелділік y=f(x) түрінде, ал бір айнымалы бірнеше (x 1, x 2 , …, x k ) айнымалыларға тәуелді болса, онда бұл функционалдық байланысу y=f(x 1, x 2 , …, x k ) түрінде беріледі. Мұндай функционалдық тәуелділіктер математикада, физикада, механикада, химияда, астрономияда т. т. жиі кездеседі. .
Функционалдық тәуелділік тек айнымалылар арасында ғана болмастан, кездейсоқ шамалар арасында да болады. Бірақ іс жүзінде кездейсоқ шамалар арасындағы функционалдық тәуелділік өте сирек беріледі, өйткені бір шаманың өзгеруі тек бір негізгі шаманың өзгеруімен ғана анықталып қоймайды. Оған есептеуге мүмкін болмайтын көптеген факторлардың әсері де болуы мүмкін. Бұл факторлар жеке тәжірибелерде кездейсоқтық қасиетке ие. Сондықтан олардың қандайда болсын заңдылықтарын ашу үшін көптеген эксперименттер жүргізуі керек. Бірақ эксперимент нәтижесінде x шамасының бір мәніне екінші y шамасының көптеген мәндері, яғни y мәндерінің жиыны немесе үлестіруі сәйкес келеді. Оның үстіне x-тің мәні өзгергенде x мәндерінің жиыны да өзгереді. Ал y мәнінің өзі болса x бойынша алынған y-тің орташа мәні төңірегінде топталады. Шамалар арасындағы мұндай тәуелділікті статистикалық тәуелділік немесе корреляциялық тәуелділік деп атайды.
Сонымен статистикалық тәуелділік туралы сөз еткенде x-тің әрбір мәніне y мәндерінің үлестіруі сәйкес келеді дейміз. Былайша айтқанда x - тің әрбір мәніне осы x - тің өзгеруіне байланысты өзгеріп отыратын ықтималдықтар мәндерінің жиыны сәйкес келеді дейді. Статистикалық тәуелділік дегенде бас жиыннан алынған таңдамадағы байланысты ұғамыз. Ал бас жиындағы шамалар арасындағы тәуелділік стохастикалық (ықтималдықтық) болады. Әрине тандама көлемі жеткілікті үлкен болса, онда белгілі шарттар орындалғанда статистикалық тәуелділік стохастикалық тәуелділікті сипаттай алады.
Шамалар арасындағы тәуелділік туралы сөз еткенде оның тығыздығы мен түрі қандай болатыны анықтау қажет болады. Тәуелділіктің тығыздығы корреляциялық коэффициент және корреляциялық қатынаспен сипатталады. Ал тәуелділіктің түрі болса графикпен, регрессия теңдеуімен немесе регрессия коэффициентімен анықталады. Шамалар арасындағы бұл байланыстар таңдамадан алынған мәліметтер бойынша көрсетіледі. Олай болса, корреляциялық анализде қарастыратын екінші мәселе тәжірибелік сипаттамалардың бас жиын немесе теориялық жиын сипаттамаларына қаншалықты дәл келуін бағалау болмақ. Бұл мәселелермен математикалық статистиканың корреляциялық теория деп аталатын бөлімі айналысады. Сонымен корреляциялық теория кездейсоқ шамалар арасындағы тәуелділіктің тығыздығы мен түрін қарастырады. Ал бұларды талдау әдістерін корреляциялық анализ деп атайды.
 Корреляциялық анализде қарастыратын негізгі шаманың (нәтижелік белгінің) бір немесе бірнеше факторларға байланысын қарастырады. Егерде нәтижелік белгінің бір факторға байланысын қарастырса, жұптық корреляция дейді де, ал екі не бірнеше факторға байланысын қарастырса, оны көп өлшемді корреляция дейді.
Корреляциялық анализде қарастыратын негізгі шаманың (нәтижелік белгінің) бір немесе бірнеше факторларға байланысын қарастырады. Егерде нәтижелік белгінің бір факторға байланысын қарастырса, жұптық корреляция дейді де, ал екі не бірнеше факторға байланысын қарастырса, оны көп өлшемді корреляция дейді.
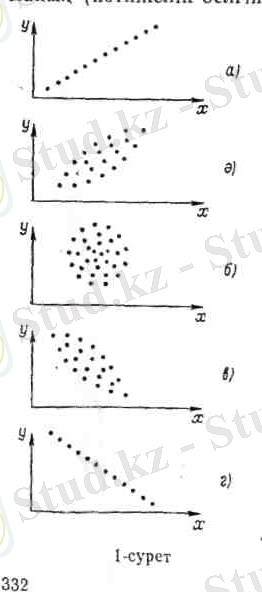
Біз талдауымызды жұптық корреляциядан бастайық. Корреляциялық анализ жасау корреляциялық таблица мәліметтеріне сүйенеді. Сонымен қатар бастапқы информацияны бір жүйеге келтірудің екінші жолы графиктік тәсіл. Графикалық тәсілдің мақсаты - корреляциялық өріс құру. Мұның үшін тікбұрышты координаттар жүйесінің абсциссалар өсіне факториалды белгілі мәндерін, ал ординаталар өсіне нәтижелік белгі мәндерін салып координаттар жазықтығындағы нүктелер жиынын анықтаймыз. Бұл жиындар түрлі формадағы өрістерді көрсетеді. Мұның кейбір түрлері 1-суретте келтірілген: а-суретте x пен y арасындағы тәуелділігі 1, ә-суретте x пен y тәуелділігі әлсіз тура түзу сызықты (r=+0. 5) болуын көрсетеді: 1, б- суретте x пен y-тің тәуелділігі түзу сызықты (r=0. 000) болуын көрсетеді: 1, в-суретте x пен y тәуелділігі әлсіз кері түзу сызықты (r=-0. 5) болуы көрсетіледі; 1, г-суретте x пен y тәуелділігі қатаң кері түзу сызықты (r=-1. 00) болуын көрсетеді. Мұндағы айнымалылар арасындағы тәуелділік тығыздығын көрсететін шама - бұл корреляциялық коэффициент.
1. 2. Корреляциялық таблица және регрессия теңдеуі.
Статистикалық бақылаулар нәтижесінде қарастырып отырған шамалар жайында мәліметтер жинастырамыз. Ол мәліметтер бойынша статистикалық байланыс таблица күйінде жасалынады. Мұндай таблицалар екі түрде болады. Бірінде ол таблица мәліметтерді санау арқылы жасалады, екіншісінде қарапайым корреляциялық таблица, корреляциялық тор немесе корреляциялық матрица күйінде болады. Егерде x-тің жиынындағы әрбір мәнін жазып оның қасына сол мәнге сәйкес y-тің мәнін жазсақ, қарапайым корреляциялық таблица аламыз:
Мұндай таблицалар практикада жиі кездеседі. Мұндағы x -тің мәні тек бір реттен ғана қайталанып отырса онда келесі есептеулерді тікелей осы таблица бойынша орындау қажет. Көп жағдайда x пен y мәндері сан рет қайталанып отырылуы мүмкін. Бұл жағдайда таблицадағы мәліметтерді қарастырып отырған x және y белгілері бойынша топтастыру керек. Топтастырудың екі тәсілі бар. Бірінші тәсілінде, 1-таблицада көрсетілгендей, белгілердің жеке мәндері бойынша, екіншісінде интервал бойынша топтастырылады
1-таблица

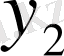
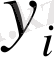
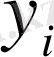
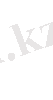
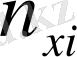
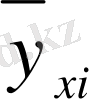
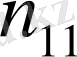
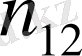
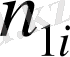
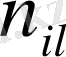
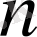 x1
x1
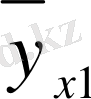
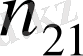
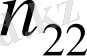
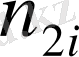
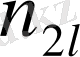
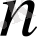 x2
x2
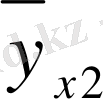
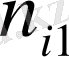
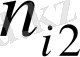
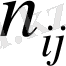
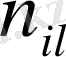
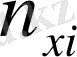
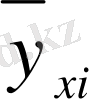
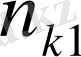
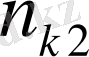
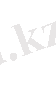
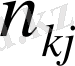

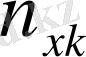
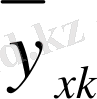

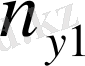
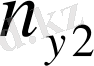
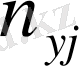
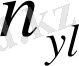
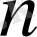
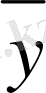
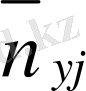
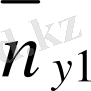
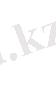
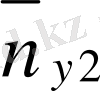
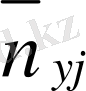
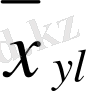
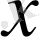
Қос индексті n ij символы (мұны кейде n xy деп те жазады) X пен Y мәндері бірдей бірнеше рет қайталанып кездескенін көрсететін жиілік саны. Мысалы, n 14 =5 десек, мұны x 1 жолы мен y 4 бағанасының қиылысуында x 1 пен y 4 мәндерінің әрқайсысы 5 реттен қайталанып кездесті деп ұғамыз. n xi арқылы x i жолы бойынша алынған сандар қосындысын көрсетілген жиілік белгіленген, яғни
n xi = n i1 + n ie + … +e ie.
n yi арқылы y j бағанасы бойынша алынған сандар қосындысы көрсететін жиілік белгіленген, яғни n yj == n 1j + n 2j + … +n kj. Барлық n 1j сандарды алдымен n xi бағанасы бойынша, одан соң n yf жолы бойынша қосып, немесе алдымен n yj жолы, одан соң n yi бағаналы бойынша қосып, немесе клеткадағы барлық n ij мәндерін (i=1, k, j=1, i) қосу арқылы n мәнін аламыз, яғни n 1j
n =
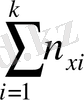 =
=
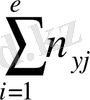 =
=

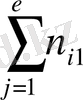 =
=
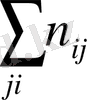
Мұндай етіп қосу, екінші жағынан, n мәнінің қаншалықты дұрыс есептелгенін де қадағалайды. Өйткені n yj жолы бойынша алынған қосынды мен бағанасы бойынша алынған қосындысы бірдей санына тең болуы тиіс.
Дербес жағдайда әрбір қатардағы сандар жиынтығы Y мәндерінің берілген мәніне сәйкес үлестіру қатарын көрсетеді (2-таблица), сондай - ақ әрбір бағандағы сандар жиынтығы X мәндерінің берілген Y j мәніне сәйкес (3-таблица) үлестіру қатарын көрсетеді.
2-таблица
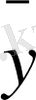
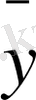 x1
x1
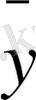 x2
x2
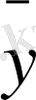 xi
xi
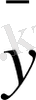 xk
xk
3-таблица
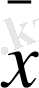
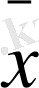 y1
y1
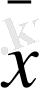 y2
y2
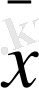 yj
yj
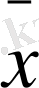 yt
yt
Интервал бойынша топтастырудан жасалған корреляциялық таблица да 1-таблицадай болады. Бұл жағдайда X және Y-тің жалпы өзгеру интервалдарын дербес ∆x және ∆y (әдетте
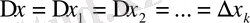 Интервалдарға бөледі, сөйтіп бұл интервалдар ортасын сәйкес және арқылы белгілеп әрі қарай 1-таблица сияқты жазылады. Мұндағы дербес шартты арифметикалық орталар бұрынна мәлім формулалармен анықталады.
Интервалдарға бөледі, сөйтіп бұл интервалдар ортасын сәйкес және арқылы белгілеп әрі қарай 1-таблица сияқты жазылады. Мұндағы дербес шартты арифметикалық орталар бұрынна мәлім формулалармен анықталады.
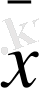 yj=
yj=
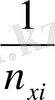
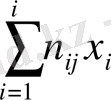 ,
j=1, 2, …,
l,
,
j=1, 2, …,
l,
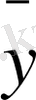 xi=
xi=
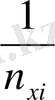
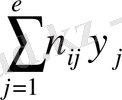 ,
i=1, 2, …,
k,
,
i=1, 2, …,
k,
Ал жалпы арифметикалық орта
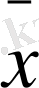 =
=
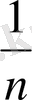
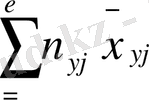 ,
,
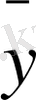 =
=
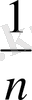

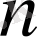 x
x
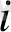
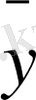 , x
, x
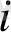
1-таблицадан айнымалы
X -тің Y әрбір мәніне Y-тің топтық арифметикалық орта мәні y
k сәйкес келіп отыр. Олай болса, айнымалы
X пен айнымалы Y-тің топтық орта мәндері арасында функционалдық байланыс болуы мүмкін, оны
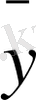 x
=f(x) түрінде жазамыз. Дәл осы сияқты, 1-таблицадан айнымалы Y-тің әрбір мәніне X-тің топтық арифметикалық ортасы
x
=f(x) түрінде жазамыз. Дәл осы сияқты, 1-таблицадан айнымалы Y-тің әрбір мәніне X-тің топтық арифметикалық ортасы
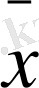 y
cәйкес келіп отырғанын байқаймыз. Олай болса, бұл жағдайда Y пен X-тің топтық орта мәндері арасындағы функционалдық тәуелділікті
y
cәйкес келіп отырғанын байқаймыз. Олай болса, бұл жағдайда Y пен X-тің топтық орта мәндері арасындағы функционалдық тәуелділікті
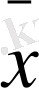 y =
y =
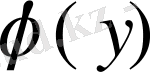 түрінде жазамыз. Мұндағы
түрінде жазамыз. Мұндағы
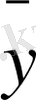 x
,
x
,
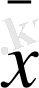 y
шартты арифметикалық орталар, біріншісінде X орындалғандағы Y - тің шартты арифметикалық ортасы болса, екіншісінде Y орындалғандағы X-тің шартты арифметикалық ортасы болып отыр.
y
шартты арифметикалық орталар, біріншісінде X орындалғандағы Y - тің шартты арифметикалық ортасы болса, екіншісінде Y орындалғандағы X-тің шартты арифметикалық ортасы болып отыр.
Сонымен екі айнымалы арасындағы корреляциялық тәуелділік деп біреуінің бір мәніне екіншісінің шартты арифметикалық орта мәні сәйкес келетін функционалдық тәуелділікті айтады. Біріншісін Y-тің X-ке, екіншісін X -тің Y-ке қатысты корреляциялық теңдеулері немесе регрессия теңдеулері деп атайды.
4-таблица
X пен Y мәндерінің әр жұбын нүктемен көрсетсек, онда 1-таблицадан корреляциялық өріс, 4-таблицадан сынық сызық аламыз. Бұл таблицадан
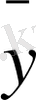 x -
тің сызқтық функциясы болуын көрсетеді. Оны
x -
тің сызқтық функциясы болуын көрсетеді. Оны
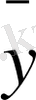 x
=ax+b түрінде жазуға болады. Егер Y-тің белгілі мәніне сәйкес X-тің арифметикалық ортасын есептесек, онда
x
=ax+b түрінде жазуға болады. Егер Y-тің белгілі мәніне сәйкес X-тің арифметикалық ортасын есептесек, онда
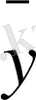 x
мәндері төмендегі 5- таблицада келтірілгендей болар еді.
x
мәндері төмендегі 5- таблицада келтірілгендей болар еді.
5-таблица
Мұның графигі де түзу сызыққа өте-мөте жуық, сондықтан олардық арасындағы байланысты
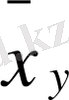 =cy+d түрінде жазуға болады. Бұлардың графигін Y-тің X-ке және X -тің Y -ке қатысты қисықтары делінеді. Ал таблицадағы статистикалық мәліметтерді суретке түсіргенде ол түзу сызыққа жақындау мүмкіндігін айттық. Бірақ сынау саны неғұрлым аз болған сайын қисықтағы заңдылықты байқау соғұрлым қиынға соғады. Оның себебі тәжірибеден алынған мәліметтер бойынша суретке салынған нұктелерді бір - бірімен қосқаннан шыққан сынық сызықтары теориялық сызықтан біресе жоғары, біресе төмен түсіп аралары алшақтап отыруы мүмкін. Сондықтан сынау санын арттырып топтастырсақ олардың аралығы кемиді. Бірақ бұл жолмен мақсатқа жету қиын, себебі іс жүзінде сынау саны шекті аз болады. Олай болса, алдымен тәжірибелік (статистикалық) мәліметтер бойынша қисықты таңдайды. Мұндай қисықтар, әрине, түзу де, парабола да, жоғары дәрежелі парабола да т. т. болуы мүмкін.
=cy+d түрінде жазуға болады. Бұлардың графигін Y-тің X-ке және X -тің Y -ке қатысты қисықтары делінеді. Ал таблицадағы статистикалық мәліметтерді суретке түсіргенде ол түзу сызыққа жақындау мүмкіндігін айттық. Бірақ сынау саны неғұрлым аз болған сайын қисықтағы заңдылықты байқау соғұрлым қиынға соғады. Оның себебі тәжірибеден алынған мәліметтер бойынша суретке салынған нұктелерді бір - бірімен қосқаннан шыққан сынық сызықтары теориялық сызықтан біресе жоғары, біресе төмен түсіп аралары алшақтап отыруы мүмкін. Сондықтан сынау санын арттырып топтастырсақ олардың аралығы кемиді. Бірақ бұл жолмен мақсатқа жету қиын, себебі іс жүзінде сынау саны шекті аз болады. Олай болса, алдымен тәжірибелік (статистикалық) мәліметтер бойынша қисықты таңдайды. Мұндай қисықтар, әрине, түзу де, парабола да, жоғары дәрежелі парабола да т. т. болуы мүмкін.
Сонымен айнымалы шамалар арасындағы өзара тәуелділікті қарастырудан бұрын оның түрлерін анықтап алу керектігі туады. Әр түрлі тәуелділіктер ішінде ең кең тараған да, қарапайым да, практикада кеңірек қолданыс тапқан да және толығырақ зерттелінгені де сызықты тәуелділік. Оның үстіне, тәуелділіктің бұл түріне түрлендіру арқылы әр түрлі қисық сызықты тәуелділіктерді әкелуге болатынын ескертеміз. Олай болса (Ляпуновтың орталық теоремасы бойынша), кейбір шарт орындалғанда Y мәндерінің - орта шартты
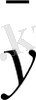 x
төңірегінде үлестіруі нормаль заңына жақын болады. Бұл айтылғаннан салдар ретінде, регрессия сызығының түзуге жақын болып шығуын, екінші сөзбен айтқанда, корреляциялық тәуелділіктің түзу сызыққа жақын болуын байқаймыз. Сондықтан да сызықты корреляцияны қалыпты корреляция деп қарастырады, мұның теориялық және практикалық мәні зор. Сонымен, статистикалық мәліметтер бойынша сызықты регрессия теңдеуін іздестірейік. Оны анықтау үшін y=ax+b сызықты теңдеуін a, b параметрлерін табуымыз керек. Бұларды табудың бірнеше әдісі бар. Біз айырымның квадраттары ең аз болу әдісін пайдаланамыз. Бұл әдіспен y=a
x
төңірегінде үлестіруі нормаль заңына жақын болады. Бұл айтылғаннан салдар ретінде, регрессия сызығының түзуге жақын болып шығуын, екінші сөзбен айтқанда, корреляциялық тәуелділіктің түзу сызыққа жақын болуын байқаймыз. Сондықтан да сызықты корреляцияны қалыпты корреляция деп қарастырады, мұның теориялық және практикалық мәні зор. Сонымен, статистикалық мәліметтер бойынша сызықты регрессия теңдеуін іздестірейік. Оны анықтау үшін y=ax+b сызықты теңдеуін a, b параметрлерін табуымыз керек. Бұларды табудың бірнеше әдісі бар. Біз айырымның квадраттары ең аз болу әдісін пайдаланамыз. Бұл әдіспен y=a
 +bx+c теңдуінің a, b, c параметрлерін, сондай-ақ n дәрежелі парабола
+bx+c теңдуінің a, b, c параметрлерін, сондай-ақ n дәрежелі парабола
y=a
n
x
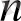 +a
n-1
x
+a
n-1
x
 +…+a
1
x+a
0
+…+a
1
x+a
0
теңдеуінің
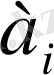 (i=0, 1, 2, …, n) параметрлерін де анықтай аламыз.
(i=0, 1, 2, …, n) параметрлерін де анықтай аламыз.
1. 3. Ең аз квадраттары әдісі
Бұл әдіс тәжірибеден алынған нәтижелерді өңдеуге байланысты түрлі есептерді шығаруға қолданылады, бірақ теориялық функцияның жалпы түрін таңдау мәселесін шешпейді. Бұл әдіс арқылы y=f(x) функциясының берілген түрінің сәйкес параметрлерінің ең ықтималды мәндерін табуға мүмкіндік аламыз. Жалпы квадраттары ең аз әдісін көпшілік жағдайда, не сызықты тәуелділіктегі y=ax+b не квадратты тәуелділіктегі y=a
 +bx+c формуласын пайдаланып, оның параметрлерін анықтайды.
+bx+c формуласын пайдаланып, оның параметрлерін анықтайды.
4-таблицада келтірілген мәліметтер бойынша тікбұрышты координаталар жүйесінде A
1
(x
1
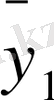 ), A
2
(x
2
y
2
), …, A
n
(x
n
, y
n
) нүктелерін салайық. Әрине A
1,
A
2
, . . . , A
n
нүктелер бір түзу бойында жатаса, онда мәселе шешілген болады, өйткені іздеген байланыс дәл сызықты болады. Сондықтан A
1,
A
2
, . . . , A
n
нүктелері бір түзу бойында жатпайды деп ұйғарамыз. Олай болса, осы нүктелерге ең жақын түзуді іздестірудің қажеттігі туады. Бұл мақсатты орындау үшін теңдеуі y=ax+b болайық. Бұл түзу бойында жататын нүктелер
), A
2
(x
2
y
2
), …, A
n
(x
n
, y
n
) нүктелерін салайық. Әрине A
1,
A
2
, . . . , A
n
нүктелер бір түзу бойында жатаса, онда мәселе шешілген болады, өйткені іздеген байланыс дәл сызықты болады. Сондықтан A
1,
A
2
, . . . , A
n
нүктелері бір түзу бойында жатпайды деп ұйғарамыз. Олай болса, осы нүктелерге ең жақын түзуді іздестірудің қажеттігі туады. Бұл мақсатты орындау үшін теңдеуі y=ax+b болайық. Бұл түзу бойында жататын нүктелер
B 1 (x 1 , ax 1 +b), B(x 2 , ax 2 +b), B n (x n , ax n +b) болсын.
Енді тәжірибелк A
i
,
(x
i
, y
i
) нүктелері мен y=ax+b түзуі бойындағы B
i
(x
i
), dx
i
+b) (
i
=1, 2, …, n) нүктелері ординаталарының айырымын (ax
i
+b) -y
i
алайық. Бұл нөлге тең емес. Сондықтан y=ax+b параметрлерін (ax
i
+b) -
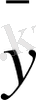 x
айырымдар квадраты ең аз болатындай етіп таңдауды қажет етеді, яғни
x
айырымдар квадраты ең аз болатындай етіп таңдауды қажет етеді, яғни
S=
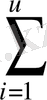 [(ax
i
+b) -y
i
]
[(ax
i
+b) -y
i
]


Мәні миннмум болуы керек (мұнда y i - мен ауыстырылды) . Ал әрбір ауытқу іздулінді параметрлерге байланысты болғандықтан, S-те a және b параметрлерінің функциясы болады, яғни
S=S(a, b) :
S(a, b) =
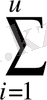 (ax
i
+b-y
i
)
(ax
i
+b-y
i
)
 =min (1)
=min (1)
болады.
Енді дифференциалдық есептеулердегі белгілі әдіс бойынша S-тің a және b бойынша алынған дербес туындыларын нөлге теңестіреміз, сонда
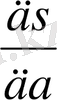 =2
=2
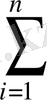 (ax
i
+b-y
i
) x
i
=0,
(ax
i
+b-y
i
) x
i
=0,
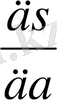 =2
=2
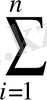 (ax
i
+b-y
i
) =0, (2)
(ax
i
+b-y
i
) =0, (2)
Мұны ықшамдап теңдеулердің мынадай қалыпты жүйесін аламыз.
a
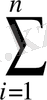 x
i
x
i
 +b
+b
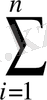 x
i
=
x
i
=
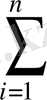 x
i
, y
i
x
i
, y
i
a
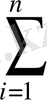 x
i
+nb=
x
i
+nb=
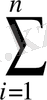 y
i
, (3)
y
i
, (3)
Мұндағы x
i
, y
i
, мәндері тәжірибеден алынған мәліметтер бойынша беріледі. Олай болса
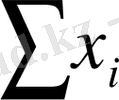 ,
,
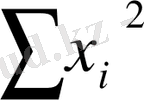 ,
,
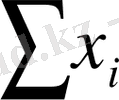 , y
i,
n мәндерін анықтау қиынға соқпайды. Сондықтан бұл (1) жүйесін a және b бойынша шешіп, олардың мәндерін анықтаймыз (бұдан былай қосындылау индексін қоймаймыз) :
, y
i,
n мәндерін анықтау қиынға соқпайды. Сондықтан бұл (1) жүйесін a және b бойынша шешіп, олардың мәндерін анықтаймыз (бұдан былай қосындылау индексін қоймаймыз) :
a=
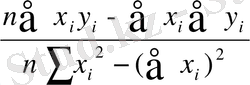 , b=
, b=
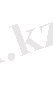
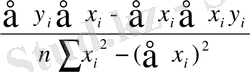 . (4)
. (4)
Ал ол қосындыларды есептеу үшін мына таблицаны пайдалану қолайлы.
6-таблица


Сызықтық теңдеу орнына мына квадраттық теңдеуді
Y=ax
 +bx+c (5)
+bx+c (5)
алсақ, онда a, b, c параметрлерінің ең ықтималды мәндерін анықтау үшін
S=
 (ax
1
(ax
1
 +bx
1
+c-y
1
)
+bx
1
+c-y
1
)
 =min
=min
Шартын қанағаттандыруы қажет. a, b, c бойынша алынған дербес туындыларын нөлге теңестіреміз, сонда
 =2
=2
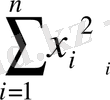 (ax
i
(ax
i
 +bx
i
+c-y
i
) =0,
+bx
i
+c-y
i
) =0,
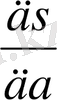 =2
=2
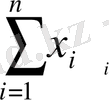 ( ax
i
( ax
i
 +bx
i
+c-y
i
) =0,
+bx
i
+c-y
i
) =0,
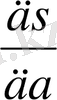 =2
=2
 (ax
i
(ax
i
 +bx
i
+c-y
i
) =0,
+bx
i
+c-y
i
) =0,
Мұндағы қалыпты жүйесі мынадай:
a
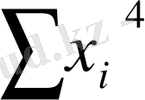 + b
+ b
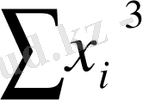 +c
+c
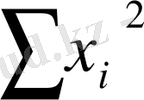 =
=
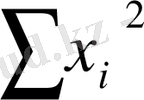 y
i
,
y
i
,
a
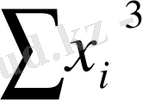 + b
+ b
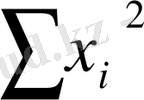 +c
+c
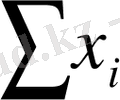 =
=
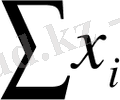 y
i
,
y
i
,
a
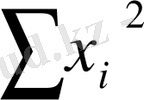 + b
+ b
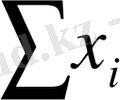 +nc
+nc
 =
=
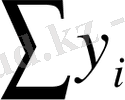 (6)
(6)
Осы жүйені шешіп, a, b және c параметрлерін анықтаймыз. Бұл теңдеулер жүйесі (6) коэффициенттерін мына таблица бойынша есептеуді ұсынамыз:
7-таблица



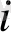 y
y
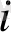
 y
y
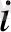

Мұндағы ең соңғы қатары әрбір бағандағы мәндер қосындысын көрсетеді. Бұл системаны жалпы түрде шешіп a, b және c мәндерін есептейді. Біз оны жазып жатпай 7-таблицадағы мәндер бойынша коэффициенттері мен берілген системаны үйреншікті тәсілмен шешу арқылы a, b және c мәндерін табамыз.
1. 4. Жиі пайданылатын функциялар мен олардың қалыпты теңдеулері
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz