Дискриминантты талдау

Дискриминантты талдау.

1. Дискриминантты талдаудың негізгі мақсаты.

2. Дискриминантты талдау есебінің қойылымы.

3. Қадамды дискриминантты талдау.

1. 1. Дискриминантты талдаудың негізгі мақсаты.

Дискриминантты талдау зерттелетін белгілердің максималды жинақталу ұстанымы бойынша көпөлшемді бақылаулардың жіктеу әдістерін қамтитін көпөлшемді статистикалық талдаудың бір тарауы болып саналады.

Дискриминантты талдауда жаңа кластерлер емес, ішкі жиын объектілері, дискриминантты айнымалылар бойынша және дискриминантты функция шамасын теңестіру негізінде, алдын ала пайда болған ішкі жиынға тиісті болатын ереже тұжырымдалады.

Екі және одан да көп жиындар (топтар) бар болатын болсын және біз, ол жиынға таңдамалы байқау жүргізе аламыз. Дискриминантты талдаудың негізгі есебі келесі түрде тұжырымдалады: осы таңдамалы байқаулар арқылы жаңа байқауды жиынтыққа тистіретін ережені құру.

М ₀ ішкі жиынын m -объектілерінің M _k ішкі жиыны бойынша үлестіру ережесін (сызықты немесе сызықты емес f ( X ) дискриминантты функцияны) құру қажет.

Дискриминантты функцияның сызықтық түрі жиі қолданылады. Бұл функция дискриминантты көбейткіштер A = ( a ₁ , a ₂ , . . . , a _p ) векторының және X _i = ( x _{i , 1} , x _{i , 2} , …, x _{i , p} ) дискриминантты айнымалылы векторлардың скалярлық көбейтіндісіне тең:

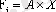
немес

F _i = a ₁ x _{i , 1} + a ₂ x _{i , 2} + … a _p x _{i , p} .

мұндағы X _i - i -ші бақылау объектінің j -ші белгілерінің дискриминантты айнымалылардың транспонирленген векторы .

Дискриминантты талдау келесі негізгі ұйғарым шарттарында орындалады:

· М жиыны екі немесе одан да көп ( q ≥ 2) M _k жиындарына жіктеледі, ол басқа топтардан x _ij айнымалымен ерекшеленеді;

· M _k әр бір ішкі жиынында кем дегенде екі объект бар ( n _k ≥ 2) ;

· N объектінің байқау саны р дискриминантты айнымалыны кем дегенде екі бірлікке үлкен болу қажет (0 < р < N -2) ;

· ( j ) объектілердің сызықтық тәуелсіздігі, яғни белгілердің біреуі басқа белгілердің сызықтық комбинациясы болмауы қажет;

· x _ij дискриминантты айнымалылардың нормальды үлестіру заңы.

Егер келтірілген тұжырымдар қанағаттандырылмайтын болса, дискриминанттық талдаудың мақсатты қолданылуы туралы мәселе қарастырылады.

Дискриминантты талдаудың басты мәселесінің бірі дискриминантты айнымалыларды және дискриминантты функция түрін анықтау. Жоғары дәрежелі, сапалы қорытынды алу үшін қадамды дискриминантты талдау қолданылады. Дискриминантты айнымалылар ретінде бақылауда болатын белгілер ғана емес, сонымен қатар факторлық талдауда анықталған басты факторлар мен алғашқы белгілер қолданылады.

Дискриминантты талдау статистикалық жиынтықтарды болжамдау да қолданылады.

Дискриминантты функцияның сызықтық түрі. Оның негізгі кезеңдері

1. Мәліметтер кестеге толтырылады:

M _k ( k = 1, 2, . . . , q ) ішкі жиынының нөмірі

Объект нөмірі i ( i = 1, 2, . . . , n _k 2)

Қасиеттері (көрсеткіш), j ( j = 1, 2, . . . , p )

х ₁

х ₂

…

х ₀

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: M ₁ ( k = 1) Ішкі жиыны

Объект нөміріi(i= 1, 2, . . . ,nk2): 1

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: 2

Объект нөміріi(i= 1, 2, . . . ,nk2):

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: …

Объект нөміріi(i= 1, 2, . . . ,nk2): …

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p): …

…

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: n ₁

Объект нөміріi(i= 1, 2, . . . ,nk2):

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: M ₂ ( k = 2) Ішкі жиыны

Объект нөміріi(i= 1, 2, . . . ,nk2): 1

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: 2

Объект нөміріi(i= 1, 2, . . . ,nk2):

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: …

Объект нөміріi(i= 1, 2, . . . ,nk2): …

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p): …

…

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: n ₂

Объект нөміріi(i= 1, 2, . . . ,nk2):

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: …

Объект нөміріi(i= 1, 2, . . . ,nk2): …

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p): …

…

…

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: M _q ( k = q ) Ішкі жиыны

Объект нөміріi(i= 1, 2, . . . ,nk2): 1

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: 2

Объект нөміріi(i= 1, 2, . . . ,nk2):

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: …

Объект нөміріi(i= 1, 2, . . . ,nk2): …

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p): …

…

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: n _q

Объект нөміріi(i= 1, 2, . . . ,nk2):

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: дискриминацияға тиісті M ₀ Ішкі жиыны

Объект нөміріi(i= 1, 2, . . . ,nk2): 1

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: 2

Объект нөміріi(i= 1, 2, . . . ,nk2):

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: …

Объект нөміріi(i= 1, 2, . . . ,nk2): …

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p): …

…

…

Mk(k= 1, 2, . . . ,q) ішкі жиынының нөмірі: m

Объект нөміріi(i= 1, 2, . . . ,nk2):

Қасиеттері (көрсеткіш),j(j= 1, 2, . . . ,p):

…

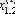
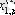
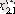
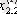
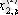
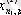
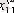
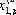
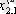
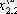
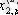
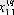
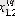
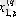
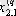
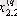
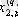
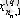
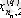
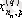
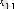
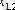
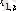
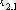
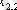
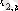
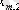
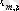
мұндағы X ^(k) - үйренуші белгілері бар матрица ( k = 1, 2, . . . , q ),

X ⁽⁰⁾ дискриминацияға тиісті жаңа m -объектілер матицасы,

р -әр бір i -ші объект сипатталатын қасиеттер саны.

Келесі шарт орындалу қажет: М жиынының N объектілер саны, дискриминацияға тиісті m объектілер саны мен объектілердің жалпы сандарының 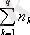қосындысына тең, яғни : 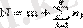, мұндағы q - үйренуші ішкі жиындар саны ( q ≥2) . практикада q =2 жағдайы жиі қолданылады.

2. 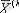орта мәнінің j -ші белгі үшін i объектілердің k -ішкі жиынында 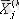элементтері анықталады ( k = 1, 2) :

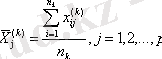
Нәтижесі вектор баған түрінде жазылады :

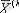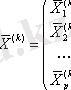
3. Әр бір үйренуші ішкі жиын үшін S ^(k) ковариационды матрицалар есептелінеді (размером p × p ) :

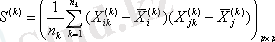
4. Келесі формула бойынша бірлескен ковариационды матрица есептелінеді:

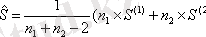
5. кері матрица анықталады:

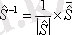
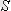- матица анықтауышы , ( ),

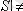6. дискриминантты көбейткіштердің вектор баған матрицасы табылады:

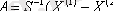
Бұл формула ең кіші квадраттар әдісімен есептелінеді.

7. Әр бір i -ші объект бойынша сәйкес ( i = 1, 2, . . . , N ) дискриминантты функциялар есептелінеді:

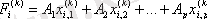
8. Анықталған мәліметтер негізінде F ^(k) орта мәндер есептелінеді:

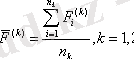
9. Дискриминантты функциялар үшін орташа мәндер анықталады

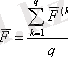
10. Ішкі жиынының М ₁ және М ₂ үлестіруі орындалады. Сол мақсатпен 7 қадамдар

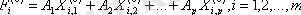
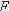жалпы орта мәнмен салыстырылады

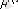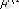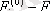Егер > , М ₀ ішкі жиынының i -ші объектісі М ₁ ішкі жиынына тиісті болады, > 0 болғанда, ал М ₂ ішкі жиынына 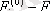< 0 болғанда.

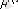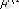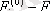Егер < , онда берілген объект М ₁ ішкі жиынына, < 0 болғанда және керісінше жағдайда М ₂ ішкі жиынына тиісті болады.

11. әрі қарай жаңа объектілердің үлестіру сапасы, дискриминантты функцияларға айнымалылардың салымы бағаланады.

Дискриминантты функцияларға белгілердің әсері дискриминантты көбейткіштер (дискриминаця коэффициенттері), дискриминантты жүктемелер немесе дискриминантты матрица бойынша бағаланады.

Дискриминантты көбейткіштер белгілердің өлшем бірлігінен тәуелді болады, сондықтан олар әрдайым бағалау үшін тиімді бола бермейді.

Дискриминантты жүктемелер F дискриминантты функция мен белгілер арасындағы деңгейлерінің корреляцияның қосақты сызықты коэффициенттері ретінде есептелінеді, сондықтан да бағалау үшін аса маңызды.

Дискриминантты матрица жіктеу нәтижелері объектінің ішкі жиыны бойынша үлестіруімен салыстыру дәрежесін сипаттайды және сапалы талдау үшін қолданылады. мұндай жағдайда F дискриминантты функция объект мәліметтері бойынша құрылады және объектінің фактілі мәліметтері формальды дискриминация нәтижесімен салыстыру барысында осы функияның сапасы тексеріледі.

Өндірістік кәсіпорын салаларының 2 тобы бойынша мәліметтер берілген:

Х ₁ - негізгі өндірістік қорлардың орташа жылдық құны, млн. ақша бірлігі;

Х ₂ - орта тізімдегі қызметшілер саны млн. ақша бірлігі;

Х ₃ - баланстық түсім, млн. ақша бірлігі.

Алғашқы мәліметтер кестеде көрсетілген:

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс