Дисперсиондық талдау
Дисперсиондық талдау.
1. Диспресиондық талдаудың негізгі ұғымдары
2. Бір фаторлы дисперсиондықт талдау
3. Екі фаторлы дисперсиондық талдау
1. 1. Дисперсиондық талдаудың негізгі ұғымдары
Көбінесе экономикалық есептерде сапалы факторлардың Х зерттелетін шамаға әсерін бағалау қажет. Мысалы, өндірістік ұйым түрлері кәсіпорын немесе фирма кірісіне маңызды немесе маңызсыз әсер ете алады. Басқа мысал ретінде әр түрлі тыңайтқыштардың тиімділік баға есебін қарастыруға болады. Берілген А факторын белгілі бір қатар деңгейлеріне бөлуге болады, ал деңгейлер ретінде өндірістік ұйымдарды немесе тыңайтқыштардың түрлерін қарастыруға болады.
Бірнеше деңгейлермен сипатталатын факторлар әсерін оқып зерттеу үшін дисперсионндық талдауды қолданылады. ( Dispersio латын сөзінен - сейілту) . Бұл әдістің маңыздылығы келесі тұжырыммен айықындалады: Х шамасының дисперсиясы екі бөлімге жіктеледі, бір бөлімі - А факторының әсерінен пайда болатын факторлы дисперсия , екінші бөлімі - кездейсоқ себептермен шартталатын қалдықты дисперсия . Егер факторлы дисперсия қалдықты дисперсиямен салыстырғанда кіші болса, онда фактор Х шамасына маңызды әсер етпейді. Дисперсионды талдау бірфакторлы және көпфакторлы болып бөлінеді.
1. 2. Бір факторлы дисперсиондық талдау
l деңгейлері бар бір кез келген А факторының әсері зерттелетін болсын. Әр бір деңгейде, яғни А факторының бір түрі үшін Х шамысының өлшемі жүргізілетін болсын. Мұндай өлшемдердің саны барлық деңгейлер үшін бірдей және q тең.
Алынған өлшем кестесін құрамыз. Соңғы жолда таңдамалы топтық орташа мәні келтірілген, ол келесі формуламен анықталады:
.
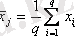1
2
…
q
х 11
х 21
…
х q1
х 12
х 22
…
х q2
…
…
…
…
х 1l
х 2l
…
х ql
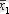
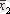
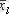
Факторлы және қалдықты дисперсия келесі формуламен анықталады:
;
.
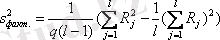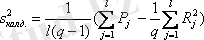мұндағы
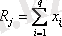- A
j
әр бір деңгей үшін
Х
шамасы бойынша мәндерінің қосындысы;
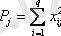- осы мәндердің квадраттарының қосындысы.
Егер
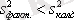болса, онда
А
факторы
Х
шамасына маңызды әсер етпейді.
Егер
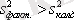болса, онда бұл дисперсиялардың маңыздылығын тексеру қажет. Ол үшін Фишер-Снедекор критерийін қолданамыз,
F
критерийдің экспериментальды мәнін анықтаймыз:
.
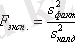Алынған мәнді Фишер-Снедекор үлестіруінің критикалық мәнімен салыстырамыз
.
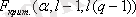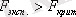шартында
А
факторы
Х
шамасына маңызды әсер етеді деген қорытындыға келеміз. Ал
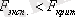болса, онда мұндай тұжырым жалған болады.
Есеп.
Кейбір А факторының әр үш деңгейі үшін өлшем жүргізілген. Дисперсиондық талдау әдісі арқылы α=0, 05 маңыздылық деңгейі үшін А факторының әсері туралы, нөлдік гипотезаны тексеру қажет. Алынған мәліметтер кестеде келтірілген.
1
2
3
4
30
32
34
28
35
39
38
36
40
38
44
42
Шешуі:
Бір факторлы дисперсиондық талдауда, эксперимент нәтижесінде алынған топтық орташа мәндер арасындағы маңыздылықты анықтауға негізделеді.
1
2
3
4
30
32
34
28
35
39
38
36
40
38
44
42
Табамыз
;
;
.
;
;
.
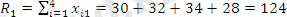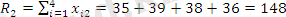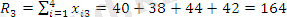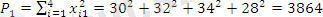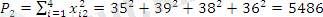Осы мәндерді қолдана отырып, сәйкес факторлы және қалдықты дисперсияны анықтаймыз:
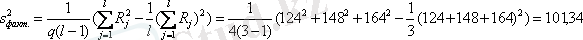
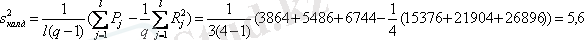
Факторлы дисперсия қалдықты дисперсиядан үлкен болғандықтан,
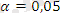маңыздылық деңгейінде олардың айырмашылық мәнін анықтау қажет. Ол үшін
F
критерийінің экспериментальды мәнін анықтаймыз:
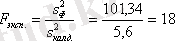
Және осы мәнді Фишер үлестріруінің критикалық мәнімен салыстырамыз
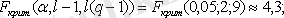
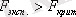болғандықтан
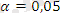маңыздылық деңгейінде алынған топтық орташалар арасындағы айырмашылық бар екенін көреміз, яғни берілген фактордың әсері айтарлықтай бар.
1. 3. Екі факторлы дисперсиондық талдау
Екі факторлы дисперсиондық талдау көп факторлы дисперсиондық талдаудың қарапайым түрі болып табылады.
Х шамысына екі А және В факторлары бір уақытта әсер ететін болсын. А факторының деңгейлер саны m ( А 1 , А 2 , …, А m ), ал В факторының - n деңгейлер саны бар болсын ( В 1 , В 2 , …, В n ) .
Қарапайымдылық үшін, бір ғана бақылау жүргізілетін эксперимент нәтижелерін қарастырамыз. Мұндай жағдайда эксперимент қорытындылары кестеде келтірілген:
Топтық орташа
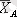
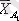
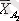
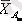
Топтық орташа
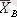
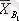
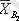
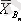
Соңғы бағанда А j әр бір деңгейіне сәйкес А фактор әсерінің топтық орташа мәндері келтірілген (жол бойынша) :
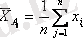
Соңғы жолда В j әр бір деңгейіне сәйкес В фактор әсерінің топтық орташа мәндері келтірілген (баған бойынша)
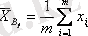
Дисперсиондық талдау әдісіне сәйкес
топты орташа мәндер арасындағы маңыздылық айырмашылықты және қалдықты дисперсияларды анықтаймыз, дисперсиялар келесі формуламен анықталады:
;
;
,
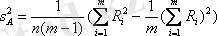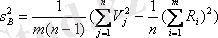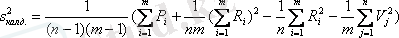мұнда
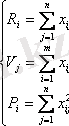
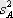және
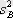факторлы дисперсиялар шамасы
Х
шама мәніне әсерін сипаттайды, ал
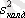қалдықты дисперсия - кездейсоқ себептердің әсерін айқындайды, әр бір фактор әсерінің маңыздылығы келесі түрде анықталады:
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz