Кластерлік талдау: ұғымы, арақашықтық метрикалары мен топтастыру әдістері


Кластерлік талдау.
1. 1. Кластерлік талдау ұғымы
Әлеуметті - экономикалық құбылыстарды анықтауда зерттеуші олардың сиппаттама көпөлшемдігімен жиі кездеседі. Нарықты сегменттеу жағдайларында, көпөлшемді көрсеткіштер бойынша мемлекеттердің типологиясын құруда, экономикалық дағдарысты болжамдауда және т. б. жағдайдарға тап болады.
Кластерлік талдаудың негізгі тағайындалуы - зерттелетін объектілер мен белгілер жиынтығының сәйкес біртекті топ немесе кластерлерге бөлінуі. Бұл дегеніміз, мәліметтерді реттеу есебінің шығарылуы және оның құрамдас бөліктерінің анықталуы. Кластерлік талдау әдісін, барлық мәліметтер санды бірдей қасиеттері бойынша топтасуға жинақталатын жағдайда да қолдануға болады.
Кластерлік талдаудың негізгі қасиеттерінің бірі - бұл талдау объектілердің бір көрсеткіші бойынша ғана емес, сонымен қатар барлық жинақталған белгілер бойынша зерттеуге, әлеуметті - экономикалық ақпараттың көпөлшемді санымен жұмыс атқаруға және оны бірден қысқартуға мүмкіндік береді.
Кластерлік талдаудың негізгі есебі Х жиынтығында қамтылған мәліметтер негізінде, G объектілер жиынтығын m бөлшектерге ( m - бүтін сан), G j әр объектілер бір тек ғана бір ішкі жиын бөлінуіне тиісті болатын, сонымен қатар бірдей кластерлерге тиісті объектілер жинақты болатындай және әр түрлі кластерлерге тиісті объектілер әр текті болып бөлінетін Q 1 , Q 2 , …, Q m кластерлерді айтамыз.
Мысалы, G - n мемлекеттерден тұратын болсын, әр біреуі ІҰӨ жан басына шаққанда ( F 1 ) сипатталады, 1 мың адамға М автокөлік санымен ( F 2 ), жан басына шаққанда электроэнергияның тұтынылуымен ( F 3 ), жан басына шаққанда болаттың тұтынылуымен ( F 4 ) және т. б. . Сонда Х 1 (өлшем векторы) бірінші мемлекет үшін сипаттама жиынтығы, Х 2 - екінші, Х 3 үшінші, және т. с. с. Есептің басты мақсаты мемлекеттерді даму деңгейлері бойынша реттеу, бөлу.
Кластерлік талдау есебінің басты мақсаты, кейбір тиімді критерийлер бойынша бөлу. Бұл критерийді мақсаттық функция ретінде қарастыруға болады. Мысалы, мақсаттық функция ретінде ауытқудың ішкі топтық қосындысының квадратын аламыз:
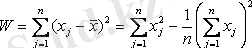
мұндағы x j - j -ші объектінің өлшемі.
1. 2. Объектілердің біртекті өлшемдері
Кластерлік талдау есебін шығару үшін жиынтық және әр тектілік ұғымдарын анықтау қажет.
х 1 және х 2 объектілердің басқарылатын белгілері бір бірімен жақын орналасқан бір топқа тиісті объектілер, біртекті деп аталады, ал берілген нормадан үлкен қашықтықта орналасқан объектілер біртексіз деп аталады. Норма қашықтығы арақашықтық метрикасы деп аталады. Объектілердің бірдей немесе әртүрлі кластерлерге түсуі Х i және Х j арақашықтық ұғымымен анықталады. d( Х i , Х j ) кері емес функциясы арақышықтық функциясы (метрика) деп аталады, егер:
а) d(Х i , Х j ) ³ 0 ;
б) d(Х i , Х j ) = 0 , сонда тек ғана сонда Х i = Х j
в) d(Х i , Х j ) = d(Х j , Х i )
Келесі функция арақашықтығы жиі кездеседі:
1. Евклид арақашықтығы
d(Х
i
, Х
j
) =
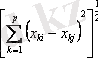
2. l
1
- норма
d
1
(Х
i
, Х
j
) =
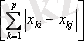
3
. l
p
- норма
d
р
(Х
i
, Х
j
) =
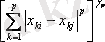
Евклидтік метрика кеңінен тараған. l 1 метрикасы есептеуде қолдану тиімді, ал l p - 1, 2, 3, арақашықтық функцияларын қамтиді.
Х 1 , Х 2 , . . . , Х n n өлшемдер p ´ n өлшемді матрица ретінде берілген болсын:
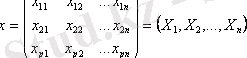
Онда
d(Х
i
, Х
j
)
жұптық векторлар арақашықтығы симметриялық матрица түрінде өрнектеледі:
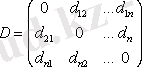
Арақашықтықққа қарама қарсы ұғымы ол, G i . және G j объектілердің жиынтығы (ұқсастығы) . S(Х i ; Х j ) = S ij кері емес функция жиынтық метрикасы деп аталады, егер:
1) 0£ S(Х i , Х j ) <1 Х i ¹ Х j үшін
2) S(Х i , Х i ) = 1
3) S(Х i , Х j ) = S(Х j , Х i )
Жиынтық өлшемдер мәнін матрица түрінде жазуға болады:

S ij шамасын жиынтық коэффициенті деп атаймыз.
1. 3. Кластерлік талдау әдістері
Қолдаңбалы әлеуметті - экономикалық зерттеулерде кластерлік талдаудың екі әдісі кеңінен тараған:
1) иерархиялық алгоритмдер әдісі
2) объектілерді анықтаудың ортаграфикалық әдісі.
Иерархиялық алгоритмдер әдісі.
Иерархиялық алгоритмдер - жалпыдан жекеге қатысты ұстанымдары бойынша топтасқан алгоритмдер тізбегі.
Иерархиялық алгоритмдер саны, тізбегі, метрика бойынша жіктеледі. Мұндай жағдайда жақын көрші, алыс көрші, орта байланыс әдістері қарастырылады.
Кез келген иерархиялық алгоритмдер әдісінің практикалық жүзеге асырылуы келесі бес амалдан тұрады:
1) х i ( i= 1, 2, …, п) барлық байқалатын объектілер тізбегін k i өзіндік кластерлерден тұратын п түрінде өрнектеу.
2) l объектімен т кластер арасындағы d lm ең кіші арақашықтық жұбын анықтау ;
3) алынған жұптардың тізбектелген бірлесуі және әр бір қадам деңгейінде кластерлер санын бір бірлікке азаюы.
4) r және кез келген q арасындағы d rq арақашықтығын анықтау ;
5) 2 - 4 қадамдарын бір және тек ғана бір ақырғы кластер алынғанға дейін тізбектеп орындау.
Кез келген иерархиялық алгоритмде, байқаланатын ішкітоптық ( d ij ) және топаралас ( d rq ) арақашықтықтар нормаланған немесе алдын ала метрикамен анықталады.
l және m кластерлерін q кластерімен біріктіруі, r түрінде тұжырымдалуы кластер арасындағы арақашықтық формуласы келесі түрде анықталады:
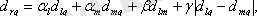
мұндағы d lq , d mq , d lm - сәйкес кластерлер арасындағы геометриялық арақашықтық;
α l , α т , β, γ-иерархиялық алгоритмдердің топтасуын анықтайтын параметрлер.
Үш критерий бойынша параметрлер мәні кестеде келтірілген
Кесте.
Топтастырудың алгоритмдері және параметрлері
«Жақын көрші»
«Алыс көрші»
«Орта көрші»
½
½
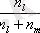
½
½
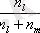
0
0
0
-½
½
0
Ортаграфикалық әдіс.
Ортаграфикалық әдісті қолдану барысында, бақыланатын белгілер саласының радиуысына, скалярлық шамаға Т сәйкес болатын, байқалатын объектілер жиынтығының жинақталуының үлкен дәрежелі тығыздық өрісі айқындалады. Келесі қадамдарды орындау кезінде топтастыру өрісі теңестіріледі. Қадамдар:
Қадам 1.
Т
радиус берілген болсын.
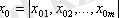 орта - нүкте негізінде, осы радиусқа тиісті нүктелер санын анықтаймыз
.
орта - нүкте негізінде, осы радиусқа тиісті нүктелер санын анықтаймыз
.
Қадам 2.
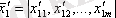 бірінші бақылау ортасына тиісті объектілер жиынтығының орта шамасын анықтаймыз.
бірінші бақылау ортасына тиісті объектілер жиынтығының орта шамасын анықтаймыз.
Қадам 3.
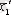 кезекті орта - нүкте деп алып, екінші бақылау ортасына тиісті
кезекті орта - нүкте деп алып, екінші бақылау ортасына тиісті
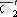 орта шамасын анықтаймыз.
орта шамасын анықтаймыз.
Қадам 4. Келтірілген есептеулер тұрақты шама алынған қадамға дейін жүргізіледі.
Қадам 5. Алынған нәтижеге талдау жүргіземіз. Соңғы айналымға кіретін объектілерді бірінші кластерлер объектілері ретінде теңестіреміз, яғни мәліметтерді алып тастаймыз.
Қадам 6. Бақылау негізінде бірініші айналымға кірмеген объектілер жаңа массив құрайды, осы массив арқылы жоғарыда келтірілген қадамдармен екінші кластерді анықтаймыз.
Қадам 7. Жұмысты аяқтаймыз. Барлық бақылауда болған объектілер кластерлерге жіктелу шартында жұмыс аяқталады.
Есеп.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz