Маусымды процесстерді болжамдау

Маусымды процесстерді болжамдау.

1. Мауысымды факторларының экономикалық процесстер динамикасын әсері.

2. Мауысымды факторлар есебімен болжамдауды құру.

3. Мультипликативті және адитивті модельдер.

Кейбір экономикалық құбылыстар табиғатына, уақыт бойынша қайталанатын даму бірқалыпсыздығы тән болады. Маусымды факторларының әсері күнтізбелік және климаттық себептерімен шартталады. Күнтізбелік себептер әсерін (демалыс және мейрам күндері, мектептегі және университеттегі каникулдар) тауардың мерекелік және демалыс күндерінде сату көлемі және жұма күндерінде транспорттық желілер ретінде қарастыруға болады. Климаттық себептерді (ауа райы шарттарымен байланысты) жыл мезгілдері бойынша электроэнергияның тұтыну көлемінен, ауылшаруашылық өнім өндірістігінен және киім мен аяқ киім сұранысынан көреміз. Жыл бойы үй салу материалдарына, киім түрлеріне, спорттық құралдарына, транспортқа, ауылшаруашылық шикізатқа, жанармайға сұраныс бірқалыпты емес. Сонымен қатар экономикалық көрсеткіштер мәндерін жұма күндері мен уақыт тәулігі бойынша ауытқуын атап өту қажет. Мысал ретінде электроэнергия тұтынуын, кітапхана оқырмандарына және мейрамхана қонақтарына қызмет көрсетуін қарастыруға болады.

Маусымдық дегеніміз экономикалық құбылыстар дамуында уақытта қайталанатын периодтылығын атаймыз. «Маусым» ұғымы кез келген систематикалық ауытқуларды болжамдауда қолданылады. Маусым факторы жыл бойынша немесе орта жылдық мәліметтерде көрсетілмейді. Маусым әсерін тоқсан, ай, жұма күндері және бір сағат бойынша ақпараттарды қамтитын уақытша қатарды зерттеуден көруге болады.

Маусымды өзгерістерді болжамдауда уақытша қатардың әр деңгейін трендтік, маусымды, кездейсоқ көрсеткіштерінің өзара байланыс нәтижелері ретінде қарастыруға болады. Олардың өзарабайланысын бағалайтын бірнеше әдістер бар. Модельдің екі түрін қарастырайық: аддитивті және мультипликативті.

Аддитивті модель құрамдастарды қосу жолымен құрылады. Маусымды ауытқулар есебімен уақытша қатар теңдеуі келесі формуламен өрнектеледі

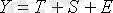. (1)

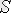Бұл модельде уақытша қатардың әр деңгейі трендтік ( ), маусымды ( ) және кездейсоқ ( ) көрсеткіштер қосындысынан тұрады.

Аддитивті модельді көрсеткіштер мәні ұзақ уақыт аралығында өзгеріссіз болған жағдайда қолданамыз.

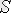Мультипликативті модель трендтік ( ), маусымды ( ) және кездейсоқ ( ) көрсеткіштерді көбейту жолымен жүзеге асырылады, уақытша қатар теңдеуі келесі формуламен анықталады

. (2)

Келтірілген екі модель біреуін таңдау маусымды ауытқулар құрамын талдау негізінен алынады. Егер ауытқулар амплитудасы жуық шамамен тұрақты болса, уақытша қатардың аддитивті моделін құрамыз, ал егер маусымды ауытқулар амплитудасы өсетін не кемитін болса, онда уақытша қатардың мультипликативті моделін құрамыз. Мұнда қатар деңгейлері маусымды көрсеткіштер мәндерінен тәуелді болады. Аддитивті модельде уақытша қатар деңгейлері әр цикл үшін тұрақты болып есептелінеді.

Аддитивті және мультипликативті модельдерді құруда қатардың әр деңгейі үшін , 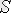және мәндерін есептеу қажет.

Модельді құру келесі қадамдардан тұрады:

1) Маусымды ауытқулар графигін салу және оны талдау.

2) Берілген қатарға жылжымалы тегістелу әдісін қолдану.

3) Маусымды көрсеткіш мәнін анықтау .

4) Берілген қатар деңгейнен маусымды көрсеткішті алып тастау және аддитивті модельде ( ), сәйкес ( ) мультипликативті модельде тегістелген мәліметтерді алу.

5) ( ) немесе ( ) деңгейлерінің аналитикалық тегістелуін және алынған тренд теңдеуі арқылы мәнін есептеу.

6) Модель бойынша алынған ( ) немесе ( ) мәндерін анықтау.

7) Берілген мәліметтерге сәйкестігінің қателік бағасы. Абсолютті немесе қатысты қателіктерді есептеу.

8) Маусымды ауытқуларды ескере отырып болжамды құру.

Есеп 1.

Кестеде 2002 жылдан 2005 жылға дейін тоқсан бойынша құқықбұзушылық мәліметтері берілген. Уақытша қатардың аддитивті моделін құрыңыз. 2006 жылдың бірінші жартыжылында құқық бұзушылық санының болжамдық бағасын анықтаңыз.

Шешімі:

Қадам 1 . Берілген қатардың графикалық талдауынан көретініміз: зеттелетін кезеңде тренд көрстекіші бар болады, сонымен қатар бірінші - екінші тоқсанды, үшінші - төртінші тоқсанмен салыстырғанда құқық бұзушылық саны төмен болғандықтан, уақытша қатардың маусымды ауытқуларының периодтылығы төртке тең.

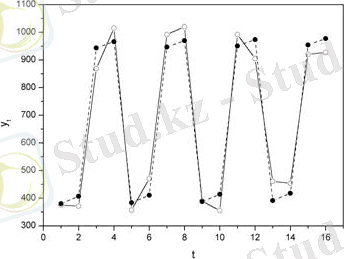
Қадам 2 . Берілген қатар деңгейлерінің тегістелуін жүргіземіз. Ол үшін төрт тоқсан үшін жылжымалы ортаны табамыз (Кесте1, баған 5) .

;

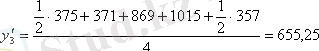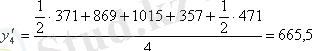; и т. д.

Алынған тегістелу мәндерінде маусымды көрсеткіштер болмайды.

Қатардың берілген деңгейлерінен жылжымалы орта мәнін аламыз. (Кесте 1, баған 6) .

Кесте 1

Жыл

тоқсан№

Құқық бұзушылық саны,

4 тоқ-қ жылжымалы орта

Жыл: 1

тоқсан№: 2

: 3

Құқық бұзушылық саны,: 4

4 тоқ-қ жылжымалы орта: 5

: 6

Жыл: 2002

тоқсан№: I

: 1

Құқық бұзушылық саны,: 375

4 тоқ-қ жылжымалы орта: -

: -

Жыл: II

тоқсан№: 2

: 371

Құқық бұзушылық саны,: -

4 тоқ-қ жылжымалы орта: -

Жыл: III

тоқсан№: 3

: 869

Құқық бұзушылық саны,: 655, 25

4 тоқ-қ жылжымалы орта: 213, 75

Жыл: IV

тоқсан№: 4

: 1015

Құқық бұзушылық саны,: 665, 5

4 тоқ-қ жылжымалы орта: 349, 5

Жыл: 2003

тоқсан№: I

: 5

Құқық бұзушылық саны,: 357

4 тоқ-қ жылжымалы орта: 693, 38

: -336, 38

Жыл: II

тоқсан№: 6

: 471

Құқық бұзушылық саны,: 709, 38

4 тоқ-қ жылжымалы орта: -238, 38

Жыл: III

тоқсан№: 7

: 992

Құқық бұзушылық саны,: 714, 13

4 тоқ-қ жылжымалы орта: 277, 88

Жыл: IV

тоқсан№: 8

: 1020

Құқық бұзушылық саны,: 703, 75

4 тоқ-қ жылжымалы орта: 316, 25

Жыл: 2004

тоқсан№: I

: 9

Құқық бұзушылық саны,: 390

4 тоқ-қ жылжымалы орта: 689, 25

: -299, 25

Жыл: II

тоқсан№: 10

: 355

Құқық бұзушылық саны,: 674, 88

4 тоқ-қ жылжымалы орта: -319, 88

Жыл: III

тоқсан№: 11

: 992

Құқық бұзушылық саны,: 669, 38

4 тоқ-қ жылжымалы орта: 322, 63

Жыл: IV

тоқсан№: 12

: 905

Құқық бұзушылық саны,: 690, 63

4 тоқ-қ жылжымалы орта: 214, 38

Жыл: 2005

тоқсан№: I

: 13

Құқық бұзушылық саны,: 461

4 тоқ-қ жылжымалы орта: 694

: -233

Жыл: II

тоқсан№: 14

: 454

Құқық бұзушылық саны,: 687, 75

4 тоқ-қ жылжымалы орта: -233, 75

Жыл: III

тоқсан№: 15

: 920

Құқық бұзушылық саны,: -

4 тоқ-қ жылжымалы орта: -

Жыл: IV

тоқсан№: 16

: 927

Құқық бұзушылық саны,: -

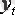
4 тоқ-қ жылжымалы орта: -

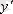
Қадам 3 . Бұл мәндерді 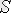маусымды көрсеткішті табу үшін қолданамыз. Ол үшін төрт жылдың әр тоқсаны бойынша орта мәндерді табамыз .

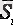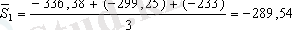
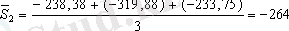
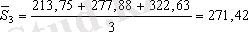
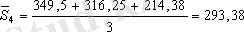
Түзететін коэффициент келесі мәнге ие:

.

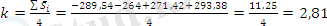маусымды көрсеткіштің түзетілген мәнін анықтаймыз:

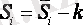
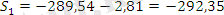
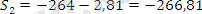
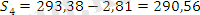
Аддитивті модельде барлық тоқсан бойынша маусымды көрсеткіштер мәні нөлге тең, яғни .

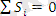Тексереміз:

.

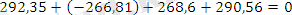Қадам 4 . маусымды көрсеткіш әсерін берілген қатардың әр деңгейінен аламыз. 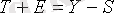шамасын аламыз (Кесте 2, баған 4) . Бұл мәндер әр уақыт үшін есептелінеді және кезедейсоқ көрсеткіш пен тенденцияны қамтиді.

: 1

: 2

: 3

: 4

: 5

: 6

: 1

: 375

: -292, 35

: 667, 35

: 1

: 667, 35

: 2

: 371

: -266, 81

: 636, 81

: 4

: 1273, 62

: 3

: 869

: 268, 6

: 600, 4

: 9

: 1801, 2

: 4

: 1015

: 290, 56

: 724, 44

: 16

: 2897, 76

: 5

: 357

: -292, 35

: 649, 35

: 25

: 3246, 75

: 6

: 471

: -266, 81

: 736, 81

: 36

: 4420, 86

: 7

: 992

: 268, 6

: 723, 40

: 49

: 5063, 8

: 8

: 1020

: 290, 56

: 729, 44

: 64

: 5835, 52

: 9

: 390

: -292, 35

: 682, 35

: 81

: 6141, 15

: 10

: 355

: -266, 81

: 621, 81

: 100

: 6218, 1

: 11

: 992

: 268, 6

: 723, 40

: 121

: 7957, 4

: 12

: 905

: 290, 56

: 614, 44

: 144

: 7373, 28

: 13

: 461

: -292, 35

: 753, 35

: 169

: 9793, 55

: 14

: 454

: -266, 81

: 720, 81

: 196

: 10091, 34

: 15

: 920

: 268, 6

: 651, 40

: 225

: 9771

: 16

: 927

: 290, 56

: 636, 44

: 256

: 10183, 04

: 136

:

:

: 10872

: 1496

: 92735, 72

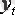
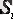
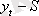
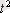
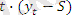
Қадам 5 . Модельдің көрсеткішін табамыз. Ол үшін ( ) қатарының сызықтық тренд арқылы аналитикалық тегістелуін жүргіземіз.

Екінші кестенің 1, 4, 5, 6 бағандарының қосындылар мәнін, сызықтық тренд үшін ең кіші квадраттар теңдеулер жүйесіне қоямыз:

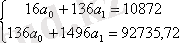
Жүйені Крамер әдісімен шығарып, а ₀ және а ₁ коэффициенттерінің мәнін табамыз

Аналитикалық тегістелу нәтижесі келесі түрде өрнектеледі:

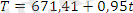
Осы теңдеуге 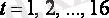, мәндерін қойғанда, әр уақыт үшін деңгейлерін табамыз (Кесте 3, баған 4) .

Кесте 3

: 1

: 2

: 3

: 4

: 5

: 6

: 7

: 8

: 1

: 375

: -292, 35

: 672, 36

: 380, 01

: -5, 01

: 25, 10

: 92799, 44

: 2

: 371

: -266, 81

: 673, 31

: 406, 5

: -35, 50

: 1260, 25

: 95252, 48

: 3

: 869

: 268, 6

: 674, 26

: 942, 86

: -73, 86

: 5455, 30

: 35861, 00

: 4

: 1015

: 290, 56

: 675, 21

: 965, 77

: 49, 23

: 2423, 59

: 112473, 04

: 5

: 357

: -292, 35

: 676, 16

: 383, 81

: -26, 81

: 718, 78

: 104090, 12

: 6

: 471

: -266, 81

: 677, 11

: 410, 3

: 60, 70

: 3684, 49

: 43526, 48

: 7

: 992

: 268, 6

: 678, 06

: 946, 66

: 45, 34

: 2055, 72

: 97575, 02

: 8

: 1020

: 290, 56

: 679, 01

: 969, 57

: 50, 43

: 2543, 18

: 115851, 74

: 9

: 390

: -292, 35

: 679, 96

: 387, 61

: 2, 39

: 5, 71

: 83885, 54

: 10

: 355

: -266, 81

: 680, 91

: 414, 1

: -59, 10

: 3492, 81

: 105384, 64

: 11

: 992

: 268, 6

: 681, 86

: 950, 46

: 41, 54

: 1725, 57

: 97575, 02

: 12

: 905

: 290, 56

: 682, 81

: 973, 37

: -68, 37

: 4674, 46

: 50791, 64

: 13

: 461

: -292, 35

: 683, 76

: 391, 41

: 69, 59

: 4842, 77

: 47799, 08

: 14

: 454

: -266, 81

: 684, 71

: 417, 9

: 36, 10

: 1303, 21

: 50908, 90

: 15

: 920

: 268, 6

: 685, 66

: 954, 26

: -34, 26

: 1173, 75

: 5, 74

: 16

: 927

: 290, 56

: 686, 61

: 977, 17

: -50, 17

: 2517, 03

: 61191, 92

:

: 10874

:

:

:

:

: 37901, 71

: 1252743, 75

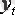
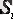
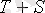
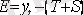
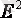
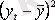
Қадам 6 . Аддитивті модель бойынша қатар деңгейлерінің мәнін табамыз. Ол үшін деңгейлеріне сәйкес тоқсан үшін маусымды көрсеткіш мәнін қосамыз. (Кесте 3, баған 5) .

Қадам 7 . Құрылған модельдің сапа бағасын тексеру үшін алынған абсолютті қателер квадратының қосындысын қолданамыз.

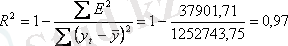
Сонымен, аддитивті модель төрт жылда тоқсан бойынша құқық бұзушылық саны жалпы уақытша қатар деңгейлерінің 97% түсіндіреді.

Қадам 8. Аддитивті модель бойынша болжамдау. 2006 жылдың бірінші жарты жылдығына құқықбұзушылық санын болжамдау қажет. Аддитивті модельде уақытша қатардың 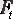болжамдық мәні, трендті және маусымды көрсеткіштердің қосындысына тең. Трендті көрсеткішті анықтау үшін тренд теңдеуін қолданамыз

.

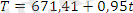алатынымыз

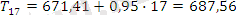
Сәйкес тоқсан бойынша маусымды көрсеткіштер: 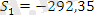және 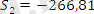. Сонымен,

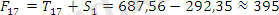
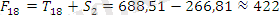
Яғни, 2006 жылдың бірінші және екінші тоқсандарында 395 және 422 құқықбұзушылық санын күтуге болады.

Есеп 2.

Кестеде 2002 жылдан 2005 жыл аралығында кеденде тіркелген құқықбұзушылық мәліметтері берілген (тоқсан бойынша) . Уақытша қатардың мультипликативті моделін құру қажет. 2006 жылдың бірінші жартыжылдығында құқықбұзушылық санының болжамдық бағасын анықтау қажет.

Шешуі:

Қадам 1 . Уақытша қатарды координаттық жазықтықта графигін саламыз:

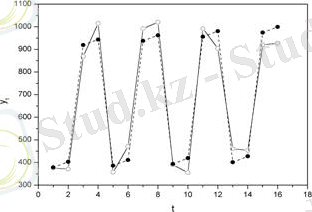
Қадам 2 . Бұл қадамдағы есептеулер толығымен аддитивті модельмен сәйкес келеді.

Маусымдық компонентаны табу үшін уақытша қатар деңгейлерін жылжымалы орта мәніне бөлеміз. (Кесте 1, баған 6) . Кесте 1

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс