Трендтік экстраполяция: сызықтық және екінші дәрежелі параболалық модельдер арқылы компанияның тоқсандық кірісін болжамдау


Тренд негізінде болжамдау.
1. Болжамды экстрапляция. Тренд ұғымы.
2. Қарапайым трендтік модельдер.
3. Экономикалық процесстер тенденцияларының болжамдау модельдері.
1. 1. Болжамды экстраполяция. Тренд ұғымы
Даму заңдылықтарын зерттеуде болжам жасауға қажет болатын ақпаратты, модельдің тренд арқылы өрнектелуінде аламыз. Болжамдаудың кез келген әдісінде, өткен кезеңде болған даму заңдылықтары, болашақ болжамданатын кезеңде де сақталады.
Экстраполяция - экономикалық шамалардың болжамданатын (күтілетін) мәні. Мәліметтердің өткен кезеңде өзгеруі туралы ақпарат негізінде, көрсеткіштерді анықтау. Математикада экстраполяция деп, экономикалық көрсеткіштің бастапқы өзгеруін сипаттайтын қисық жалғасын айтамыз.
Берілген ақпарат бойынша, белгілі бір уақыт аралығында қарастырылатын белгі ішіндегі, кейбір қол жетпейтін мәндерді анықтау интерполяция деп аталады.
Уақытша қатарда, тенденцияның бар болған жағдайында, қатар деңгейлерін уақыт функциясы деп қарастыруға болады:
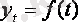
мұндағы
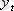 -
t уақытында аналитикалық теңдеуіне сәйкес есептелген динамикалық қатар деңгейлері.
-
t уақытында аналитикалық теңдеуіне сәйкес есептелген динамикалық қатар деңгейлері.
Динамикалық қатар деңгейлерінің, t уақыт факторынан тәуелділігін өрнектейтін теңдеу - тренд теңдеуі деп аталады .
Модель түрі зерттеу мақсатынан таңдалады және даму құбылысының көрсеткішін анықтайтын теориялық талдауда, сонымен қатар динамика қатарының графикалық бейнесінде негізделу қажет .
1. 2. Қарапайым трендтік модельдер
Қарапайым трендтік модельдер:
• сызықтық функция - түзу сызық
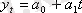
• 2-ретті қисық (парабола)
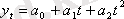
мұндағы а 0 , a 1 , a 2 - теңдеу параметрлері;
t - уақыт.
Бірінші функция түрі таңдап алынады (түзу сызық, көрсеткіштік функция, 2-ретті парабола және т. б. ) одан кейін оның параметрлері анықталады.
Параметрлерді бағалау ең кіші квадраттар әдісімен анықталады: теңдеулер саны полином параметрлерінің санына сәйкес болатын нормальды теңдеулер жүйесі құрылады. Сызықтық тренд үшін нормальды теңдеулер жүйесі келесі түрде өрнектеледі :
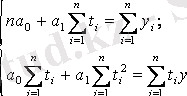
мұндағы n - динамика қатарының деңгейлері;
t - уақыт факторының реттік нөмірмен шартты белгіленуі. Уақыт санауы бірден есептелінеді;
у - динамика қатарының нақты деңгейі.
1. 3. Экономикалық процесстер тенденцияларының болжамдау модельдері
Трендтік модельдер параметрлерін қолмен (ручная) есептеу тәсілі жеңілдей түсуі мүмкін, егер координаттар басын динамика қатарының орта мәніне ауыстыратын болсақ.
Егер динамикалық қатарда деңгейлер саны тақ ( n=2p+1 ) болса, онда уақытша кезеңдер келесі түрде белгіленеді:
t = -p, …, -3, -2, -1, 0, 1, 2, 3, …, p.
Ал, егер динамикалық қатарда деңгейлер саны жұп ( n=2p ) болса, онда уақытша кезеңдер келесі түрде белгіленеді:
t = -(2p-1), …, -5, -3, -1, 1, 3, 5, …, (2p-1) .
Координаттар басын динамика қатарының орта мәніне аустырғаннан кейін
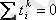 болады, мұндағы
k
- тақ сан, дәреже көрсеткіші.
болады, мұндағы
k
- тақ сан, дәреже көрсеткіші.
Болжамдаудың мұндай тәсілі, нормальды теңдеулер жүйесінің сәйкес функция параметрлерін табу процесін жеңілдетеді:
Функция
Атауы
Функция
түрі
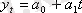
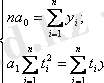
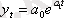
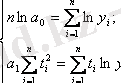
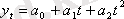
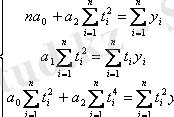
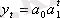
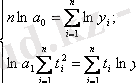
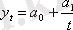
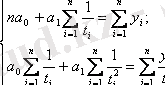
Есеп.
Компания кірісінің тоқсан бойынша мәліметтері берілген.
Компания кірісі,
Компания кірісі,
Компания кірісі,
Қатар тенденциясы келесі түрде сипатталады деп ұйғарып, келесі (16-шы) тоқсандағы кіріс болжамын есептеңіз:
а) сызықтық модель
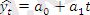 ;
;
б) параболалық модель
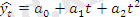 .
.
Шешуі:
а) Сызықтық тренд коэффициенттерін анықтау үшін нормальды теңдеулер жүйесінен алынған өрнекті қолданамыз, яғни координаттар басын қатардың орта мүшесіне ауыстырамыз. Динамика қатарының деңгейлер саны тақ болғандықтан (n=15), координаттар басын қатардың орта деңгейі - сегізінші деңгей деп есептейміз, сәйкес t=0. Жоғары деңгейлер -1 қадаммен, төменгі деңгейлер +1 қадаммен белгіленеді.
Кестеде қажет болатын қосымша есептеулер келтірілген.
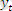
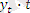
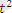
Сызықтық тренд теңдеуінің параметрлерін табу үшін нормальды теңдеулер жүйесін қолданамыз
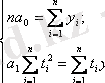
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz