Уақытша қатарлардың тегістелуі
Уақытша қатарлардың тегістелуі.
1. Жылжымалы орта бойынша уақытша қатардың тегістелуі.
2. Экспоненциалды тегістелу.
1. 1. Жылжымалы орта бойынша уақытша қатардың тегістелуі
Динамикалық қатарларды талдау кезеңінде пайда болатын мәселелердің бірі - зерттелетін құбылыстың негізгі тенденциясын анықтау болып табылады. Кейбір жағдайда бұл мәселе динамика көрсеткіштерінде анық көрінеді, ал басқа жағдайларда ауытқулар (тербелістер) барысында бұл көрсеткіштерді анықтау қиынға соғады.
Осы көрсеткіштерді анықтауда қолданылатын тәсілдердің бірі - уақытша қатарларадың тегістелуі. Біл тәсілдің мақсаты деп, уақытша қатарлардың берілген деңгейлерін ауытқу әсерінің кіші дәрежесіне ие болатын есеп деңгейлерімен ауыстыруды айтамыз. Бұл тәсіл объект дамуының нақты сурет болжамын береді.
Жылжымалы орта кездейсоқ және кезеңді ауытқуларды тегістеуге, сонымен қатар құбылыс зерттелуінде бар болатын даму тенденцияларын ашып көрсетуге мүмкіндік береді. Сондықтан уақытша қатардың бұл көрсеткіші маңызды болып саналады.
Бірінші кезеңде тегістелу интервалының ұзындығын анықтау қажет
l
. Тегістелу аралығы кеңірек болған сайын, үлкен дәрежедегі тербелістер сіңіріледі, және даму тенденциясы бірқалыпты болады. Тербелістер күшті болған сайын тегістелу аралығы кеңірек болуы қажет. Сондықтан тегістелу аралығын
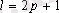тақ сан түрінде алу ыңғайлы, бұл жағдайда алынған жылжымалы орта мәні, аралықтың орта деңгейіне сәйкес келеді және келесі формуламен айқындалады:
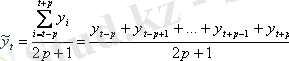
мұндағы
-
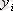i
-ші деңгейдің берілген мәні,
-
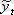t
уақытындағы жылжымалы орта мәні, 2
p
+1 - интервал ұзындығы.
Жылжымалы орта әдісінің артықшылықтары:
- жылжымалы орта зерттелетін қатар мәндеріне жуық тренд функциясын анықтайды;
- зерттелетін қатарға жаңа мәндер қосылуы мүмкін;
- тренд функция есебі жеңіл жолмен шешіледі.
Жылжымалы орта әдісінің жетіспеушілігіне мына жағдай жатады, жылжу кезеңін өсіру барысында, уақытша қатарларды талдаудың кейбір әдістерінде (мысалы, спектрлік талдау барысында) шеткі қатар деңгейлері туралы ақпарат жоғалады.
Есеп.
Берілген 10 жылдық өнім динамикалары негізінде 3 және 5 жылдық жылжымалы орта мәндерін табыңыз.
Есептеу нәтижелерін салыстырыңыз. Тегістелудің барлық графикалық әдістерін көрсетіңіз және берілген уақытша қатар мәндерімен салыстырыңыз.
Шешуі:
Есеп кестесін толтырамыз:
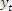
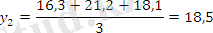
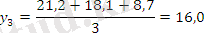
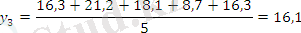
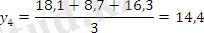
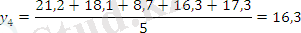
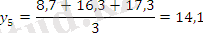
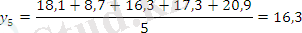
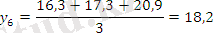
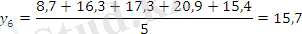
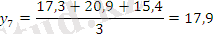
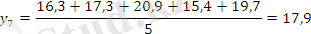
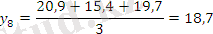
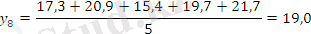
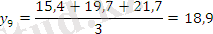
Тегістелудің графикалық суреттелуі:
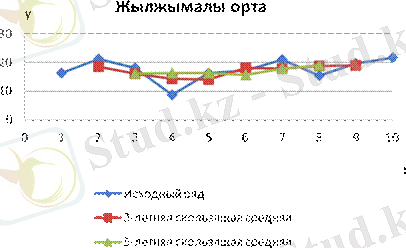
3- және 5- жылдық жылжымалы орта мәндерін салыстырғанда, 5- жылдық жылжымалы орта көбірек тегіс болатынын көреміз.
1. 2. Экспоненциалды тегістелу
Уақытша қатарлардың тегістелуі экспоненциалды тегістелу әдісімен жүзеге асырылады. Бұл әдістің мәні келесі түрде тұжырымдалады: тегістелген деңгейді табу мәселесінде - тек қана, айқын салмақпен алынған қатардың алғашқы деңгейлері қолданылады, сонымен қатар уақыт мезетінен алыстаған сайын бақылау салмағы кемиді. Егер алғашқы уақытша қатарлар
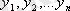үшін сәйкес болатын тегістелген деңгейлерді S
t
деп белгілейтін болсақ, мұнда t=1, …,
п
,
онда экспоненциалды тегістелу рекуррентті арақатынасымен айқындалады:
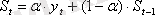
мұндағы α - тегістелу параметрі, 0 < α < 1, (1-α) шамасы дисконттау коэффициенті деп аталады. Әдетте экономикалық есептердің уақытша қатарларында тегістелу параметркөлемін 0, 1 ден 0, 3 ке дейінгі аралықта таңдайды.
S 0 бастапқы параметрін, қатардың бірінші деңгей мәніне немесе бірінші орналасқан бірнеше деңгейлердің арифметикалық орта мәндеріне тең деп аламыз. S 0 шамасының бұл таңдауы, бірінші деңгейлер үшін тегістелген уақытша қатары мен бастапқы уақытша қатарының келісуін қамсыздандырады. Егер, қатардың оң жақ соңына келгенде, бастапқы мағынадан тегістелген мәндер мағынасы маңызды шамаға өзгеретін болса, онда α басқа тегістелу параметріне көшу қажет.
Есеп.
Кестеде жоғары оқу мекемелер оқытушыларының саны (мың адам) жылдар бойынша берілген. Экспоненциалды орта арқылы, тегістелу параметрін α=0, 1 және α=0, 3 деп алып, уақытша қатар тегістелуін жүргізіңіз. Есептеу нәтижелері бойынша қай қатар көбірек тегіс болатынын анықтаңыз және оның графигін салыңыз.
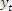
Шешуі:
α=0, 1 болған жағдайда:
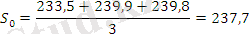
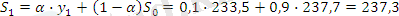
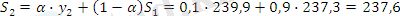
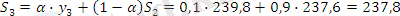
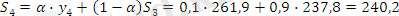
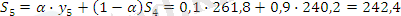
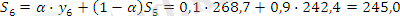
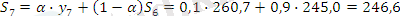
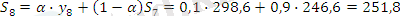
α =0, 3 болған жағдайда:
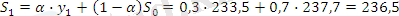
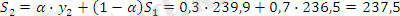
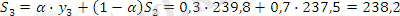
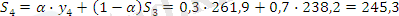
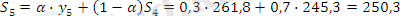
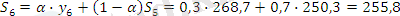
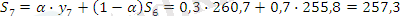
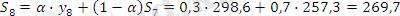
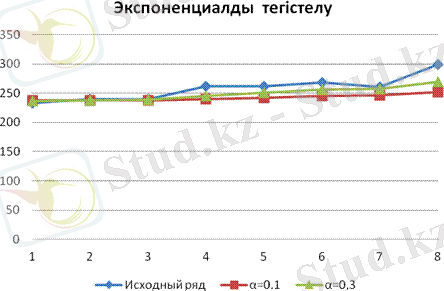
Жүргізілген есептеу бойынша α=0, 1 жағдайында уақытша қатар көбірек тегіс болатынын көреміз, дәл осы жағдайда ең үлкен дәрежелі кездейсоқ тербелістер сіңіріледі.
Тегістелудің графикалық бейнесі суретте келтірілген:
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz