Қазіргі заман мектебінде математикадан білім беру

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 45 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

АБАЙ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ
БЕКІТЕМІН
Физика-математика факультеті
Математиканың оқыту теориясы мен әдістемесі кафедра
меңгерушісі
Көксалов Қ.К.
26 тамыз 2010 ж.

Білім алушыларға арналған пәннің
оқу-әдістемелік кешені
Қазіргі заман мектебінде математикадан білім беру

1-Лекция Қазіргі заман мектеп математикасы мен математикалық ғылым
Пәннің мақсаты болашақ мектеп мұғалімдері – студенттердің негізгі
математикалық курстар бойынша алған білімдерін жалпылап, мектеп
математикасының қазіргі замандағы концепциялары, фәлсафалық мәселелері
жөнінде мағлұмат беру; білім, білік және дағдыларына қойылатын талаптарды
білу, меңгеру және оны үздіксіз тексеру; студенттерді Қазақстанда өтіп
жатқан білім беру саласындағы реформаларға сәйкес мәселелерді зерттеуге
машықтандыру және мектеп оқушыларын есеп шығаруға үйретудің жолдары жөнінде
соңғы әдістемелік ұғымдарын, жалпы мәдени құзіреттерін қалыптастыру болып
табылады.
1 бөлім. Қазіргі заман мектеп математикасының қағидалары мен
категориялары
Қазіргі заман мектеп математикасының фәлсәфалық, тарихи, педагогикалық-
психологиялық мәселелері
1.1.Қазіргі заман мектеп математикасы мен математикалық ғылым.
Жалпы сипаттама Қазіргі заман мектеп математикасының басты
мәселесі.
Қазіргі заман мектеп математикасының категориялары мен қағидаларының
жүйесі.
Қазіргі заман математикасы мен математикалық ғылым.
Қазіргі заман математикасы деп 19 ғасырдың екінші жартысынан бастап
осы күнге дейінгі уақыт аралығындағы даму кезеңі үстіндегі математиканы
айтады.
Қазіргі заман математикасы ғылымдардың тілі болып табылады.
Математика (mathēmatikě) – грек тіліндегі mathēma – ғылым деген сөзден
шыққан, нақты дүниенің кеңістіктік формалары мен сандық қатынастары
оқылатын (Ф.Энгельс) ғылым.
17 ғасырға дейін негізінде сандар, тұрақты шамалар мен қарапайым
фигуралар жөніндегі ғылым болды. Онда оқылатын шамалар (ұзындықтар,
аудандар, көлемдер т.б.) тұрақты шамалар ретінде қарастырылып келді. Осы
кезеңде арифметика, геометрия, кейінірек алгебра мен тригонометрия және
математикалық талдаудың жеке әдістері пайда болды. Математика есеп-қисап,
сауда, жер өлшеу жұмыстары, астрономия, сәулет өнерінде т.б. жұмыстарда
қолданылды. 17 және 18 ғасырларда жаратылыстану ғылымдары мен техниканың
(теңізде жүзу, астрономия, баллистика, гидравлика т.б.) қатты қарқынмен
дамуы математикаға қозғалыс пен өлшеу идеяларының, әсіресе айнымалы шамалар
мен функционалдық тәуелділік және олардың арасындағы байланыс формаларының
енуіне әкелді. Бұл өз кезегінде аналитикалық геометрияның, дифференциал
және интеграл есептеулердің пайда болуына әсер етті. 18 ғасырда
дифференциал теңдеулер теориясы, дифференциал геометрия пайда болып дами
бастады. 19-20 ғасырларда математика абстракцияның жаңа сатысына көтерілді.
Кәдімгі шамалар мен сандар қазіргі заман алгебрасының жеке мәселері ғана
болып қалды. Геометрия, Н.И.Лобачевскийдің идеясымен, евклидтік кеңістік
тек геометрияның жеке тармағы ғана болып табылатын кеңістікті зерттеуге
көшеді. Математиканың теориялық зерттеулерінің қорытындыларын практикада
қолдану – қойылған сұраққа жауапты сандық формада алуды талап етеді. Осыған
байланысты 19-20 ғасырларда математиканың сандық әдістері оның жеке өзіндік
саласы – Есептеу математикасы болып бөлініп шықты. Бірқатар қиын және көп
есептеулерді талап ететін есептерді қарапайым түрге келтіру және шешуін
жылдамдатуға ұмтылыс есептегіш машиналардың шығуына әсер етті.
Математиканың өзінің дамуының талаптары, ғылымның әртүрлі салаларының
математизациялануы, практикалық қолданыстың көптеген сфераларына
математикалық әдістердің енуі, есептеу техникасының тез қарқынмен дамуы
бірқатар жаңа математикалық пәндердің пайда болуына әкелді. Мысалы: ойындар
теориясы, ақпараттар теориясы, дискреттік математика, тиімді басқару
теориясы, графалар теориясы (математиканың бөлімі, оның ерекшелігі –
нысандарды зерттеуге геометриялық тұрғыдан келетіндігі; графалар
теориясының негізгі ұғымы – төбелер (нүктелер) жиыны және кейбір төбелерді
қос-қостан қосатын қабырғалар (байланыстар) арқылы беріледі).
Қазіргі заман математикасының категориялары мен принциперінің
жүйесі.
Категориялар (katēgoria деген грек сөзінен шығып, пікір; белгі дегенді
білдіретін философиялық термин) – нақты дүние мен таным құбылыстарының
мәні бар ортақ қаситеттері мен қатынастарын бейнелейтін ең жалпы және
фундаментальдік (түбтік, негізгі) ұғымдар.
Категориялар таным мен қоғамдық практиканың тарихи дамуын жалпылау
нәтижесі ретінде пайда болды. Диалектиканың негізгі категориялары:
материя, қозғалыс, кеңістік пен уақыт, сапа, саны, қайшылық, себептілік,
қажеттілік пен кездейсоқтылық, құрамы мен формасы, мүмкіндік пен нақтылық,
мәнділік пен құбылыс т.б.
Қосарланған категориялар: қажеттілік және кездейсоқтық, себеп пен
салдар, мүмкіндік пен шындық, форма мен мазмұн – диалектиканың қосымша
заңдары болып табылады.
Қазіргі заман математикасының категориялары (негізгі ұғымдары): сан,
форма, кеңістік пен уақыт, тұрақты шамалар мен айнымалылар, өлшемдер мен
қатынастар, сәйкестіліктер, абстракциялық т.б.
Фәлсафаның үш әмбебап заңдары: бірлік және қарама-қарсылықтарды болдармау
заңы (неге дамиды? бастауы қайда?), сандық өзгерістердің сапалық
өзгерістерге өту заңы (қалай?) және қарама-қарсылықты теріске шығару заңы
(даму бағыты? Қайда әкеледі?) – дамуды суреттейді.
Қағидалар (principius – бастау, негіз деген латын сөзінен) – 1) қандай да
бір теорияның, оқудың, ғылымның, дүниетанымның, саяси ұйымның негізгі,
бұрынғы қалпы (бастауы), 2) адамның нақты дүниеге қатынасын, тәртібінің
нормалары мен қатынасын анықтайтын ішкі сенімі, 3) қандай да бір
қондырғының, машинаның құрылысының немесе әрекетінің негізі.
Қазіргі заман математикасының қағидалары фәлсафа мен адамның дүниемен
практикалық қатынасының прициптеріне (дамыту принципі, жалпы байланыс
принципі, тарихилық принципі, себеп-салдар принципі, жүйелілік принципі)
сүйене отырып, дүниеге көзқарас, методологиялық және танымдық функцияларын
орындайды.
Диалектика – дамудың жалпы теориясы, – (грек. dialektikế (téchē) –
әңгіме, талас жүргізу өнері) – нақты дүниенің құбылыстарын дамуын олардың
дамунда, өзіндік даму барысында танудың теориясы мен әдісі, әрі табиғаттың,
қоғам мен ойлаудың ең жалпы заңдары жөніндегі ғылым.
Метафизика – диалектикаға қарсы метафизика болып табылады. Оның
метафизика деп аталу себебі, ол Аристотелден қалған мұрада физикадан кейін
баяндалатындығына байланысты.

Софистика – (софизм грек тілінде sophisma – қақпан, өтірік, басқатыру
дегенді білдіреді) – қорытындының негізі сағым, логикалық және семантикалық
(тілдік мазмұнынан, яғни мәнінен) талдаудың жеткіліксіздігінен пайда
болатын, таза субьективті әсерден туатын, жорамал дәлелдеуді пайдаланатын
философиялық зерттеу әдістерінің бірі.

Математикада қолданылатын софизмдер қатені дұрыс түсінуге, есептер
шығаруда сондай қателер жібермеуге үйретеді. Осыған мысал келтірейік

1. Есеп. 5 = 1 софизмін дәлелдеуге тырысып, 5 пен 1-ден бөлек-бөлек
бірдей сан 3-ті шегереміз. Теңдеудің екі жағында шыққан 2 және - 2 сандарын
квадраттасақ, екеуінен де 4 деген бірдей сан аламыз.

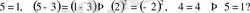
Ендеше алдыңғы алынған сандар 1 мен 5 тең болуы керек. Қате қайдан
кетті?
Шешуі: Квадраттардың теңдігінен сол сандардың өздерінің теңдігі
шықпайды.
2. Есеп. софизмін дәлелдеп, қатесін табыңыз
Шешуі: 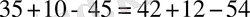сандық тепе-теңдікті қарастырайық. Оң жағындағы және сол
жағындағы ортақ көбейткіштерді жақша сыртына шығарсақ: 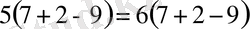. Осы теңдеудің
екі жағын жақша ішіндегі ортақ көбейткішке бөлсек: 5 = 6. Қате қайда?
Жауабы: 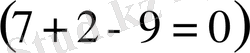-ге бөлуге болмайды
Эклектика – (грек тіліндегі eklektikós – таңдаушы деген сөзден шыққан)
әрқилы, кейде тіпті қарама-қарсы принциптерді, көзқарастарды, теорияларды,
көркем элементтерді т.б. механикалық байланыстыру (сәулет өнері мен көркем
шығармаларда тарихи стилдерді пайдалану.
Диалектика, софистика, эклектика, метафизика философияның зерттеу
әдістері болып табылады.

2-Лекция Қазіргі заман мектеп математиканың пәні, әдістері, функциялары.
Мектеп математика теориясының пәні және әдістері. Мектеп
математика ғылымының құрылымы. Мектеп математикалық теориясының
функциялары.
Қазіргі заман мектеп математикасының салалары. Математика тарихының
методологиялық негізі – диалектикалық материализм болып табылады.
Қазіргі заман математикасының басты көкейкесті мәселелері: абстракциялылық,
шексіздік, гуманитарлық білімдерді математизациялау т.б.
Философияны кейбір көкейкесті мәселелерін қарастыра кетейік.
1. Онтология – дүние мен тіршіліктің құрылуын зерттеудің көкейкесті
мәселелері.
2. Гносеология – дүниені танудың көкейкесті мәселелері.
3. Аксиология – қазына тұтудың көкейкесті мәселелері.
4. Праксиология – адамның практикалық түрлендіру әрекетінің көкейкесті
мәселелері
5. Логика, этика, саясат, эстетика т.б.
Логика деген сөз грек тілінен аударғанда келесі екі мағынасы бар сөзді
білдіреді:
1. Қисын. Мысалы істің қисыны, қисынның жоқтығы.
2. Ойлау туралы ғылым.
Ал, логикалық деген сөз қисындылық, қонымдылық дегенді білдіреді.
Логика (грек. logike), дәлелдеу мен теріске шығару әдістері жөніндегі
ғылым; әрбіреуінде белгілі бір әдіс қарастырылатын ғылыми теориялар
жиынтығы.
Логиканың негізін салушы Аристотель болып есептеледі. Түрлері:
индуктивтік логика, дедуктивтік логика. Дедуктивтік логика: классикалық,
интуиционистік, конструктивтік, модальдық, ж.б. болып бөленеді.
Осы теориялардың бәрін ақиқат тұжырымдар – шарттардан ақиқат тұжырымдар
– салдарға әкелетін тұжырымдар секілді әдістерді белгілі бір тәртіппен
жасалған тізімге енгізуге ұмтылыс біріктіреді (каталогқа енгізу); каталогқа
енгізу әдетте логикалық есептеу төңірегінде іске асырылады.
Ғылыми-техникалық үрдістің үдеу жағдайында есептеу математикасындағы,
автоматтар теориясындағы, лингвистикадағы, информатикадағы т.б. логиканың
қосымшасы ерекше роль атқарады.
Диалектикалық логика – объективтік дүние мен таным дамуының адам ойы
көрінісіндегі заңдары мен формалары жөніндегі оқу.
Математикалық логика – ойлау (қорытындылау) әдістерін математикалық
әдістермен зерттеулерді қамтитын дедуктивтік логика; ойлаудың дедуктивтік
ойлау әдістерінің математикалық теориясы.
Математикалық логика деп, кейде математикада пайдаланатын логиканы
айтады.
Дедукция (лат. deduction – қорытындылау) – логика ережесі бойынша
қортынды шығару (пікір айту), бөліктері логикалық қатынаспен байланысқан ой
тізбегі (пікір). Дедукцияның бастамасы (алғы шарт) аксиомалар, постулаттар
немесе жалпы (жалпы) тұжырымдау сипаттары бар жай болжамдар, ал соңы алғы
шарттардан, теоремалардан шығатын салдарлар (жеке) болып табылады.
Пікір логикасы – логиканың бөлімі, мұнда пікірлердің шындығы мен
жалғандығы элементарлық (ары қарай бөлінбейтін және талданбайтын) деп
аталатын пікірлерден конъюкция (және), дизъюнкция (немесе), теріске
шығару (жоқ, емес), импликация (егер..., онда...) ж.б. логикалық
операциялар көмегімен пікірлер құру негізінде қарастырылады немесе
шешіледі.
Ойлау дегеніміз өзінің даму үстінде зор кәмілдікке жеткен материяның
жемісі.
Логика – дұрыс ойлаудың заңдары мен формалары жөніндегі ғылым.
Логиканың заңдары: Тепе-теңдік заңы; Қарама-қайшылық заңы (қайшылық
емес заңы); Үшіншіні болдырмау заңы; Жеткілікті негіз заңы (Лейбниц).
Бірінші заң – тепе-теңдік заңы: кезкелген ұғым мен пікір өзіне өзі теңбе-
тең. Әртүрлі ойларды теңестіруге болмайды, тепе-тең ойларды тепе-тең емес
деп қабылдауға болмайды. Бұл заң логикалық ойлаудың анықтылығын қамтамасыз
етеді.
Екінші заң – Қарама-қайшылық (қарама-қайшылық емес) заңы: екі қарама-
қарсы пікір бір кезде ақиқат бола алмайды, олардың кем дегенде біреуінің
жалған болуы қажет. Қандай да бір объект жөнінде бір нәрсені тұжырымдай
отырып, біз сол уақытта, сол қатынаста алынған, сол объект туралы сол
тұжырымды керіге шығарып, өзімізге-өзіміз қарсы бола алмаймыз. Бұл заң
ойлаудың қайшылықсыз және тізбекті болуын, өзінің және басқалардың
пікіріндегі әртүрлі қайшылықтарды белгілеп түзетуді қамтамасыз етеді.
Үшінші заң – үшіншіні болдырмау заңы: екі қарама қарсы пікір бір уақытта
екеуі бірдей жалған бола алмайды. Олардың бірі ақиқат болуы қажет, екіншісі
жалған болуы қажет, үшінші пікір болмайды. Біріне бірі қайшы екі пікірдің
бірін дұрыс қабылдаудан жалтаруға және олардың арасынан үшінші нәрсені
іздеуге болмайды. Бұл заң логикалық ойлаудың бірмәнді болуына жеткізеді.
Төртінші заң – жеткілікті негіз заңы: кезкелген ақиқат пікірдің
жеткілікті негізі бар. Қандай да бір ойдың жеткілікті негізі болып,
қарастырылып отырған ойдың ақиқаттығы шығатын, бұрын тексеруден өткен және
қабылданған кезкелген басқа ой бола алады. Бұл заң ойлаудың негізді болуын
қамтамасыз етеді. Біз нені болса да тұжырымдағанда әрқашан өз пікірімізді
дәлелдеуге тиіспіз, яғни өз пікіріміздің дұрыстығын дәлелдейтін жеткілікті
негізіміз болуы қажет.
Қазіргі заман математикасының салалары. БЭС наука.
Қазіргі заманда ғылымдар: табиғаттану, қоғамдық ғылымдар, техникалық
ғылымдар болып бөлінеді.
Қазіргі заман математикасында: комплекс айнымалы функцияларының
теориясы, группалар теориясы, проективтік және евклидтік емес геометрия,
жиындар теориясы, математикалық логика, ықтималдар теориясы, функциялық
талдау, есептеу техникасы және басқа да жаңа пәндер пайда болды.
3-Лекция Қазіргі заман мектеп математикасы ғылым ретінде: фәлсафалық
аспект. Математика адам мәдениетінің феномені ретінде. Математика
мен фәлсафа
Математика ғылымдар тілі ретінде. Математика модельдер жүйесі
ретінде.Философтар мен оқымыстылардың математикаға көзқарастарының
әрқилылығы. Математика адам мәдениетінің феномені ретінде.
Мәдениет дегеніміз – (cultura деген лат. тіліінен аударғанда жасау,
тәрбиелеу, оқыту, даму, құрмет тұту) қоғамның, адамның шығармашылық күші
мен қабілетінің тарихи анықтамасы, қоғамның даму деңгейі, адамдардың өмірі
мен қызметін және олардың арасындағы қарым-қатынастарды ұйымдастырудың
түрлері мен формасында, сонымен бірге олар жасайтын материалдық және рухани
қазыналардан көрініс табады.
Мәдениет ұғымы тарихи дәуірді (мысалы, антикалық мәдениет), нақты бір
қоғамды, халықтарды, және ұлттарды (мысалы, майя мәдениеті), сонымен бірге
өмір мен әрететтің ерекше сферасын (мысалы, еңбек, саясат мәдениеті, көркем
мәдениет) суреттеу үшін қолданылады; ал бұдан тарлау мағынада – адамдардың
рухани өмірінің сферасы. Мәдениет өзіне адамдардың әрекетінің заттың
қорытындысын (мысалы, машиналар, ғимараттар, таным, шығарма, өнер
туындыларының норма мен адамгершілік қағидаларының (моральдың), құқықтың
қорытындылары), сонымен бірге әрекет кезінде (білім, білік, дағды,
интеллект, адамгершілік және эстетикалық даму деңгейі, дүниетанымы,
адамдардың қарым-қатынасытарының әдістері мен формалары) іске асатын
адамдардың күші мен қабілетін қамтиды.
Материалдық және рухани мәдениет органикалық бірлікте болады. Әрбір
қоғамдық-экономикалық формация мәдениеттің белгілі бір түрімен сипатталады
және бір формациядан екіншісіне өткенде өзгеріске ұшырайды; мұнда
бұрынғының мәдениетінің барлық құндылықтары мұраға қалдырылады.
Мәдени революция – В.И. Ленин енгізген ұғым – социалистік революциядан
кейінгі мәдениетті дамыту; бұл надандықты жою және халыққа білім беру мен
оқу-ағарту саласының жаңа жүйесін құру, буржуазиялық интеллегенцияны қайта
тәрбиелеу мен социалістік интеллегенцияны құру; ескі идеологияның әсерін
жою; социалистік мәдениет құру, тіршілікті жаңаша құруды қамтиды.
Математика ғылымы адам мәдениетінің құрамды бөлігі, феномені болып
табылады.
Математика мен фәлсафа.
Метематика ғылым ретінде мынадай фәлсафалық үш функцияны орындайды:
мәдениет саласы, дүниені тану әдісі, әлеуметтік институт (оқу орындары,
ғылыми қоғамдар, академиялар, лабораториялар, журналдар, кітаптер т.б.).
Басқа ғылымдар сияқты математикаға ерекше сипаты болады:
- әмбебаптылық – білімді хабарлайды, бұл адам оны қалай алғанының шартында
барлық универсум үшін ақиқат.
- Фрагментарлық – тіршілікті тұтас емес, нақты дүниенің әртүрлі
фрагменттерін, оның параметрлерін зерттей отырып, өзі әртүрлі ғылымдарға
бөлінеді. Жалпымәнділік; жеке тұлғаға тәуелді еместілік; жүйелілік;
аяқталмағандық; ескімен байланыс; сын қөзбен қараушылық; сенімділік ;
ғылыми шындықтың адамгершілік-этикалық жағдайдан қалыстығы; рационалдылық;
сезімділік.
Бұлар қос-қостан алты жұп құрайды: әмбебаптылық-фрагментарлық;
жалпымәнділік – жеке тұлғаға тәуелді еместілік, жүйелілік-аяқталмағандық,
ескімен байланыс-сын қөзбен қараушылық, сенімділік-ғылыми шындықтың
адамгершілік-этикалық жағдайдан қалыстығы, рационалдылық-сезімділік.
Ғылым – атқаратын функциясы нақтылық туралы нысанды білімдерді жүйеге
кетіру болып табылатын адам әрекетінің сферасы; қоғамдық сана формаларының
бірі; жаңа білімдерді алу жөніндегі әрекеттерді қарастыра отырып, дүниенің
ғылыми көрінісінің негізінде жатқан білімдердің қосындысы болып табылатын
қорытындысын да қоса қарастырады.
Ғылым нақты дүние жөніндегі объективтік білімдердің теориясын жасау
және теориялық жүйелеу функциясы болып табылатын адам әрекетінің функциясы
ретінде анықталады.
Ғылымның негізгі үш аспектісі:
- ғылыми-әлеуметтік институт ретінде (ғалымдар қоғамы, ғылыми мекемелер
жиынтығы, ғылыми қызмет көрсету құрылымы т. б.);
- ғылыми қорытынды ретінде (ғылыми білімдер);
- ғылым – үрдіс ретінде (ғылыми қызмет) қарастырылады.
Ғылымның қорытынды ретіндегі қасиеттерін қарастырайық.
1) Кумулятивтік сипаттамасы – жаңа білімдер бұрынғылармен бірігеді, оларды
толықтырады, теріске шығармайды. Жаңа білім, зерттеуші өзіне дейінгі
білімді толық меңгергенде ғана, алынады.
2) Ғылымның дифференциациясы (бөлшектелуі) мен интеграциясы (бірігуі).
Мысалы, Д.И.Менделеевтің периодтық жүйе элементтерінің өзара байланыста
болуы т. б.
Негізгі мақсаты – оның оқу пәнін құрастыратын нақтылықтың процесстері
мен құбылыстарын оның ашатын заңдарының негізінде суреттеу, түсіндірі және
болжау. Ғылым жүйесі табиғаттану, қоғамдық және техникалық болып шартты
түрде бөлінеді. 17 ғасырдан бастап ғылыми қызметтер көлемі әрбір 10-15
жылда шамамен екі есеге артады (ғылыми жаңалықтар, ғылыми ақпараттар,
ғылыми қызметкерлер саны).
Ғылымның дамуында экстенсивті және революциялық кезеңдер алмасып
отырады. Ғылымның оның құрылымын, таным принциптерін, категориялар мен
әдістерін, сонымен бірге оны ұйымдастыру формаларын ғылыми революциялар
қарастырады. Ғылымға оның дифференциациясы мен интеграциясының процестерін
сәйкестердіру; фундаментальды және қолданбалы зерттеулердің дамуы тән.
Қалыптасқан ғылыми-техникалық революция жағдайында, ғылымға жетекші роль
беріледі.
Математика мен жаратылыстану. Математика ғылымдар тілі ретінде.
Қазіргі заманда тек біраз ғалымдар ғана өздерін тек математикпіз
немесе физикпіз, немесе биологтармыз деп атай алады. Бұлар өз мамандықтарын
жете түсініп, ол туралы әдебиеттері түгел дерлік оқып шыққан және оның
салаларын да жақсы біледі. Бірақ, осы тар мамандықтан сырттай сұраққа ол
жауап беруді өзінің басқа мамандық иесі болып табылатын әріптесіне жолдай
салады. Пәндердің тар арнаға түсірулуі, математиканы басқа ғылымдарды жан-
жақты зерттеу кезінде пайдалануда қиындықтарға әкеледі. Әдетте, бір ғылымда
бұрынан белгілі, классикаға айналып кеткен қорытындылардың, іргелес
ғылымда әлі қолданыс таппауы ғылымның дамуына тоқырау әкеледі. Пәндердің
шекарасындағы ашылып жатқан үлкен жаңалықтар қазіргі уақытта мамандардың
пән аралық байланысты игеруін, математиканың ғылымдарды зерттеуге
қолданылуын іске асыруда кейде математиктердің де сол білімді игеруін
немесе ғалымдардың ұжым құрып жұмыс істеуін талап етеді. Мұндай ұжымдардағы
әрбір ғалым өз пәнін жетік меңгерумен қатар іргелес пәнді де жетік меңгеруі
қажет. Мысалы, математиктен физиологиялық эксперимент жасау ұсынылмағанмен,
ол осы экспериментті дұрыс түсініп математикалық есептеу арқылы дәлелдеп
немесе теріске шығара белуі қажет. Ал физиологтан математикалық формуланы
дәлелдеу қажет етілмегенмен де, ол математикке зерттеу бағытын түсінідіріп,
жол сілтей білуі қажет.

4-Лекция. Қазіргі замандағы мектеп математикасының алдыңғы тарихы мен даму
кезеңдері
Математикалық білімдердің пайда болуы себептері мен түп
тамыры.Гректерге дейінгі цивилизациялардағы математика. Ерте
Грецияда математиканың теоретикалық ғылым ретінде қалыптасуы.
Евклиддің Бастамасы, Диофанттың Арифметикасы, Шулва-Сутрада
трактатындағы дәстүрлік геометрия.Арабтық Шығыстағы ортағасырлық
математика. Жаңа білімдер негізі ретіндегі араб цифрлары.
Алгебраның жеке пән болып бөлінуі. Орта ғасырдағы және қайта
өрлеу дәуіріндегі математика. Жаңа уақыттың басындағы ғылыми-техникалық
революция. Алгебра саласындағы жетістіктер және олардың
жаратылыстанудағы мәні. XVIII ғасырдағы математикалық талдаудың
дамуы. Талдау негізінің проблемасы. Ф.Клейннің Эрлангендік
бағдарламасы геометрияның құрылымына жаңа көзқарас ретінде.
Математикалық логика. Д.Гильберттің геометрия негіздері. Ықтималдар
теориясының мәселелері.
Неміс классикалық философиясының бастаушысы Иммануил Канттың (1724-
1804) ойынша – зерттеуші дегеніміз – табиғатқа интеллектуалдық қызығушылық
танытатын, табиғатты бағындыруды көздеген адам; Математика – дүниенің
мүмкін нұсқаларын зерттеуге адамзаттың бағыттаған ғылымы; Әрбір
жаратылыстану ғылымында қаншалықты математика болса, соншалақты шындық
бар.
Позитивизм мен социологияның негізін салушылардың бірі, француз
философы Огюст Конттың (1798-1857) ойынша – Адамзаттың интеллектуалдық
эволюциясының үш кезеңін бөліп көрсеткен: теологиялық кезең, метафизикалық
немесе абстракциялық кезең және позитивтік немесе ғылыми кезең. О.Конт
ғылымдардың негізін бөліп көрсеткен, бұлар: математика, астрономия, физика,
химия, биология, социология.
Альберт Эйнштейн өзінің атақты заңдарын математикалық формулалар арқылы
ашқанмен математикаға көзқарасы күрделі болған: Нақты дүниеге қандай да
бір қатысы бар математиканың заңдары сенімді емес, ал сенімді математикалық
заңдардың нақты дүниеге қатысы жоқ; Мәнін түсінбей математикалық пәндерді
игерудің таң қаларлық мүмкіндігі бар;
Николай Николаевич Лузин математиканы өткен ғасырларда тоқырап қалған
дайын ғылым ретінде емес, оны творчестволық даму процесінде қарастырып,
шешілмеген проблемаларына назар аударып, гипотезалар ұсынған. Ол Михайл
Васильевич Ломоносов атындағы Мәскеу Мемлекеттік университетіндегі ұзақ
жылдар бойы жүргізген өз лекцияларында тыңдаушыларын олардың болашақта
зерттеу жұмыстарына үлкен үлес қосатындықтарына сендіре білген.
Француз математигі, физигі және философы Жюль Анри Пуанкаре (Poincaré)
(1854-1912) Математикада анық емес ойлар үшін символдар жоқ; Математика
– әртүрлі заттарды бір ғана атпен атау өнері деген.
Француз математигі және механигі Луи Пуансо (Poinsot) (1777-1859).
Ағылшын философы, логикі, математик, қоғам қайраткері және Нобель
силығының лауреаты (1950 ж. – әдебиет бойынша) Бертран Рассель (Russel)
(1872-1970) математиканы логикалық тұрғыдан негіздеу мақсатында логиканың
дедуктивтік-аксиматикалық құрылымын дамытқан. Математикалық логиканы
негіздеуші – Математиканың негізі деп аталатын еңбектің авторы (А.
Уайтхедпен авторлық бірлестікте). Таза математика – біз не жөнінде айтып
отырғанымызды білмейтін ғылым...;
Италян табиғат суретшісі, скульпторы, архитекторы, оқымыстысы,
инженері Леонардо да Винчи (Leonardo da Vinci) (1452-1519) көркем тілдің
жаңа кұралдарын теоретикалық жалпылаулармен сәйкестей отырып Биік Қайта
өрлеу дәуірінің гуманистік идеалдарына сәйкес келетін адам образын жасаған.
Құпия кешкі ас (1495-1497) деген еңбегінде жоғары этикалық мазмұн -
композициялардың қатаң заңдылықтарында, кейіпкерлердің қимылдары мен
мимикасының (бет-жүз қимылы) анық жүйесінде бейнеленген. Әйел сұлулығының
гуманистік идеялары Моно Лизаның (Джаконда, 1503 жыл шамасы) портретінде
жүзеге асырылған. Оның көптеген жаңалықтары, жобалары, математика
саласындағы көптеген эксперименттік зерттеулері бар. Ол табиғатты танып-
білуде тәжірибе жасаудың шешуші мәні бар болатындығын жақтаған.
Математикалық ғылымдардың ешбірін қолдануға болмайтын және математикамен
ешбір байланысы жоқ ғылымдарға ешбір сенім жоқ.
Италян математигі Леонардо Пизанский (Leonardo Pisano) (Fibonacci) (1180-
1240) Абактың кітабы деген еңбегінің негізінде араб математиктерінің
жетістіктерін мазмұндаған, сол арқылы олармен Батыс Еуропаның танысуына
ықпал еткен.
Николай Иванович Лобачевский (1792-1856): Дүниедегінің бәрін өлшеуге,
есептеуге болады.
Ұлы орыс математигі евклидтік емес геометрияның негізін қалаушы, Қазан
университетінің 1827-1846 жылдар уақыт аралығындағы ректоры
Н.И.Лобачевкийдің замандастарының қолдауын таппаған еңбектері мен ашқан
жаңалықтары – 2 мың жылдан аса уақыт бойы Евклидтік геометрия негізін
қаланған кеңістік жөніндегі ұғымға төңкеріс жасап, математикалық ойдың
дамуына үлкен ықпал еткен.
Михайл Васильевич Ломоносов.
Француз математигі, механик және физигі Симеон Дени Пуассонның (1781-
1840) (Poisson) ойынша: Өмір екі нәрсемен ажарланады: математикамен
айналысу және математиканы оқыту. Оның атымен: пуассон коэффициенті
(серпімділік модулі) және пуассон теңдеуі (, мұндағы - Лаплас
операторы, түріндегі жеке тундылары бар теңдеулер) аталған.
Математика модельдер жүйесі ретінде. Математика және
техника. Математика мен дін. Математика мен өнер.
Философтар мен оқымыстылардың математикаға көзқарастарының әрқилылығы
(И.Кант, О.Конт, А.Пуанкаре, А.Эйнштейн, Н.Н.Лузин).

5-Лекция Математикалық теорияның ішкі және сыртқы даму факторлары
Қазіргі заман мектеп математикасының даму заңдылықтары
Математикалық теорияның ішкі және сыртқы даму факторлары.
Таза математика апологиясы (Г.Харди). Ұлттық математика мектептері
және ұлттық математикалық дәстүрлердің ерекшеліктері. Т.Кунның ғылыми
революция концепциясы. Математикалық білімнің біреуден екіншіге
берілуінің сипаттамасы. Ғылыми зерттеу бағдарламаларының концепциясын
математиканың дамуын зерттеуге қолдану мүмкіндігі. Математикадағы
фальсификаторлардың пайда болу проблемасы.
Жиындар теориясы – математиканың негізі ретінде: Г.Кантор және
жиындардың аңқау теориясын жасау. Жиындар теориясының
парадокстерінің ашылуы және олардың философиялық жағын түсіну.
Математикалық логика - математиканы негіздеу құралы және
математиканың негізі ретінде. Г.Фрегенің математикалық ойлау
табиғатына көзкарасы. Математиканы логикалық бір ізге салу
бағдарламасы.
Жиындар теориясы – жиындардың жалпы қасиеттері оқылатын математиканың
бөлімі. Жиындар теориясы математиканың көптеген бөлімдерінің негізін
құрайды; ол математиканың өзінің пәнін түсінуге терең ықпал еткен.
XIX ғасырдың екінші жартысына дейін жиындар математикалық ұғым
ретінде қарастырылмаған. Неміс математигі Георг Кантор математиканы
стандартизациялаудың өзіндік бағдарламасын жасады. Мұнда кезкелген
математикалық (объект) нысан қандай да бір жиын ретінде қарастырылуы
қажет.
Мысалы, натурал сан, Кантордың айтуынша, натурал қатар деп аталатын,
Пеано аксиомаларын қанағаттандыратын қатар жиынның бір ғана элементі
ретінді қарастырылуы қажет. Бірақ Кантор өзінің бағдарламасын жиындар
теориясы демей жиындар жөніндеғі оқу (Mengenlehre) деп атаған. Кантор
бағдарламасы көптеген математикатердің, соның ішінде, әсіресе, Леопольд
Кронекердің қарсылықтарына кездесті. Ол математикалық нысан ретінде
жиындарға тек натурал сандар және оған қатыстылар ғана тиісті деген
пікірде болды (Құдай натурал сандарды жаратты – ал, басқалардың бәрін адам
қолымен жсалған деген пікірі белгілі). Дегенмен Готлоб Фреге және Давид
Гильберт математиканы теориялық-жиындық тілге көшіру жөніндегі Кантордың
идеясын қолдады.
Бірақ, жиындарға амалдар қолдануда Кантор қондырғысы (математиканың
мәні оның бостандығында принципіндегі оның өзінің пікірі) берік еместігін
байқатты. Атап айтқанда, бірқатар теориялық-жиындық антиномдар байқалды:
кейбір теориялық-жиындық көрсеткіштерді пайдаланған кезде кейбір тұжырымдар
өздерінің теріске шығаруларымен бірге дәлелденетіні анықталды. Сонда,
классикалық логиканың пікірі бойынша кез келген тұжырым дәлелденеді.
Антиномдар Кантор бағдарламасының толық қирауын көрсетті.
Жиындардың аксиоматикалық теориясы.
Д.Гильберттің геометрия негіздері және геометрияның формальді
аксиоматикалық пән ретінде қалыптаса басталуы.
XX ғасырдың басында Бертран Рассел жиындардың аңқау теориясын оқу
барысында қарама-қайшылыққа келді (Рассел парадоксы). Осылайша,
жиындардың аңқау теориясының және сонымен байланысты канторлық
математиканы стандартизациялау бағдарламасының да дұрыс еместігі көрінді.
Математикалық логика – математиканы негіздеу құралы және
математиканың негізі ретінде.
Г. Фрегенің математикалық ойлау табиғатына көзкарасы.
Математиканы логикалық бір ізге салу бағдарламасы.
Д. Гильберттің геометрия негіздері және геометрияның формальді
аксиоматикалық пән ретінде қалыптаса басталуы.
XIX ғасырдың аяғы мен XX ғасырдың ортасындағы ықтималдар теориясының
фәлсафалық мәселелері.

6-Лекция Математика әдіснамасы, эволюциясы
Математиканың методологиялық әдістері. Математиканың әдіснамасының
(методологиясының) ішкі және сыртқы функциялары, оның болжамдық бағытталуы.
Оқушылардың математика сабақтарында логикалық ойлауын дамыту үшін қызықты
математиканы пайдаланудың әдістемесі (1 кесте) оқытудың негізгі үрдісінен
туындайтын дамыта отырып оқыту үрдісіне сүйенеді. Осы кестеде келтірілген
әдістемелерге түсініктеме берейік:
1.Оқыту жоспарын оқушылардың қызығушылығын тудырып, логикалық ойлауын
дамытатындай етіп құру, – деп, біз әрбір сабақты оқушыларды қызықтырудан
бастауды, сабақта өтілетін барлық материалдарды қызықты етуді айтамыз.
Қызығушылық оқушыны білімге құштарлыққа жетелейді.
2.Оқушыларды өзіне-өзі сұрақ қоюға үйрету, – деп, біз оқушылар алған
білімдерін, сабақ кезінде ғана емес, басқа кездерде де жиі-жиі есіне
түсіріп, өзіне-өзі сұрақ қоюға дағдыландыруды түсінеміз. Мысалы,
А.Эйнштейнге салыстыру теориясын қалай ашқандығы жөнінде сұрақ қойғанда, ол
: Мен ол туралы жиі ойлап жүрдім – деп жауап берген. Бұл санның сапаға
өтуіне ықпал жасайды, қоршаған ортаны танып-білуге жетелейді.
1-кесте – Оқу үрдісі

Оқыту ҚЫЗЫҚТЫ МАТЕМАТИКА
Дамыта оқыту Мазмұнның жүйелілігі мен біртұтастығы, қиындықтың жоғары
үрдісі деңгейінде оқыту; теориялық білімдердің жетекшілік ролі,
материалдарды тез қарқынмен оқыту; баланың болмысын дамытуға
бағытталған жүйелі жұмыс; оқушының оқу үрдісін ұғынуы,
рационалды және эмоционалды сфераларды іске қосу;
вариативтілік және жеке тіл табысу.
Математиканы Оқыту жоспарын оқушылардың қызығушылығын тудырып, логикалық
оқытудың ойлауын дамытатындай етіп құру.
қызықты Оқушыларды өзіне-өзі сұрақ қоюға үйрету.
әдістемесі Қызықты математиканы өтілетін тақырыпқа байланыста
қолдану.
Күнделікті өмір практикасынан алынған қызықты есептер
шығару.
Стандарт емес қызықты есептерді шығаруға дағдыландыру.
Қиын ситуациялардан шығуға үйтететін классикалық қызықты
есептерді математика сабақтарында оқып-үйрену.
Оқушыларды кеңістік ұғымымен, қарапайым стереометриялық
фигуралармен ерте жастан таныстыру.
Дұрыс емес формалы фигуралардың ауданын, т. б. өлшемдерін
жуықтап есептеуді 15 жасқа дейін үйрету.
Бір есепті әртүрлі формада (кесте, график, сурет, схема
т.б.) беру.
Бірінен бірі туындайтын құрылымдық есептерге машықтандыру.
Қисынды табуға үйрету (басқатыру есептері).
Математика сабақтарында компьютердің мүмкіндіктерін
логикалық ойлауды дамыту үшін пайдалану т. б.
Даму Оқулықтар, қызықты есептер жинағы, Адам ↔ табиғат;
кеңістігі кітаптар, сөздіктер, оқыту адам ↔ қоғам;
бағдарламалары, дидактикалық адам ↔ адам;
әдебиеттер, зерттеулердің нәтижелері,адам ↔ өзі;
жаңа ақпарат құралдары, компьютер т. адам ↔ компьютер
б.
Іс-әрекет Біріге қызығып әрекет етуШығармашылықпен айналысу
ЛОГИКАЛЫҚ ОЙЛАУ

3. Қызықты математиканы өтілетін тақырыпқа байланыста қолдану, - дегенде,
біз қызықты есептер тақырыпқа байланысты құрылуы керектігі жөнінде
айтпақпыз.
4. Күнделікті өмір практикасынан алынған қызықты есептер шығару, - дегенде,
біз математиканы өмірмен, қоршаған ортамен байланыстыру – математиканы
қызықсыз, қиын пән деген ұғымнан арылту жөнінде айтып отырмыз.
Анықтаушы эксперименті кезінде алынған диагностикалық сауалнама кезінде
оқушылардың 10%-ы ғана математиканы, 25%-ы гуманитарлық пәндерді, ал 65%-ы
жаратылыстану пәндерін қалайтындықтарын айтты.
5. Стандарт емес қызықты есептерді шығаруға дағдыландыру, - деп біз
біріншіден стандарт емес ойлауға ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.