КОМПАКТЫ ЖИЫНДАР ҰҒЫМЫ

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ . . . 5

1 КОМПАКТЫ ЖИЫНДАР ҰҒЫМЫ . . . 6

Метрикалық кеңістіктегі жинақтылық . . . 6
Метрикалық кеңістіктердегі компакты жиындар. . …… . . . 9

1. 3 Компактылық ұғымы үшін Арцель теоремасы . . . 11

1. 4 Сызықты нормаланған кеңістіктегі компакты жиындар …… . . . ……13

1. 5 $L^{p}\lbrack a, b\rbrack$ кеңістігіндегі компактылық . . …. . 14

ҚОРЫТЫНДЫ . . . 15

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР . . . 16

КІРІСПЕ

Жұмыстың өзектілігі. Алдын ала кейбір қарапайым ұғымдардың метрикалық кеңістіктегі анықтамасын еске салайық. X - кез-келген метрикалық кеңістік болсын.

Анықтама 1 $AϲX$ кез-келген жиын және, $\left\{ G_{\lambda} \right\}, \ \lambda \in ʌ$ ашық жиындардың кез-келген үйірі болсын. Мұнда ʌ индекс λ мәндерін қабылдайтын сандар жиыны. Жалпы жағдайда ол саналымсыз жиын болуы мүмкін. Егер ʌ саналымды жиын болса, онда, $\left\{ G_{\lambda} \right\}, \ \lambda \in ʌ$ жиындар тізбегі, ал жалпы жағдайда жиындар үйірі болады.

Егер кез-келген $x \in A$ элементі $G_{\lambda}$ , жиындарының ең болмағанда бірінде жататын болса, онда $\left\{ G_{\lambda} \right\}$ , үйірі A жиынын бүркейді дейміз.

Анықтама 2 $AϲX$ жиынының барлық элементтерін қамтитын радиусы ақырлы шар бар болса, онда А шенелген жиын деп аталады.

Басқаша айтқанда, қайсыбір $x_{0} \in X$ элементі мен $r \in (0; \infty)$ саны үшін $A \subset O_{r}(x_{0})$ болса, онда А шенелген жиын болғаны.

Математикалық анализден белгілі екі тұжырымды еске алайық:

1. Больцано-Вейерштрасс теоремасы. Нақты сандардың шенелген ақырсыз жиынының ең болмағанда бір шектік нүктесі бар.

2. Гейне - Борель леммасы. Ақырлы кесіндіні бүркейтін интервалдар жиынынан, сол кесіндіні әлі де бүркейтін ақырлы ішжиын бөліп алуға болады.

Бұл тұжырымдар $R^{n}$ метрикалық кеңістігінде де орындалады. Бірақөлшемі ақырсыз кеңістіктерге бұл принциптерді бұлжытпай таратуға болмайды екен. Компакт жиын ұғымы - осы тұжырымдардың жалпы метрикалық кеңістік тұрғысыңдағы бірегей жалпыламасы.

Анықтама 3 Егер метрикалық кеңістіктегі А жиынының кез - келген ақырсыз ішкі жиынында жинақты тізбек бар болса, онда А шала компакт жиын деп аталады. Ал осындай тізбектің шегі А жиынында жатса, онда А компакт жиын деп аталады.

Бұл анықтамадан компакт жиын тұйық жиын, сондай-ақ, шала компакт жиынның тұйыктауы компакт жиын екені көрінеді. Дербес жағдайда, егер А компакт тізбек болса, оның жинақты ішкі тізбегі бар болады.

Кеңістік анықталған Xжиыны компакт жиын болса, онда бұл метрикалық кеңістік компакт деп аталады.

Арцель теоремасы $C\lbrack a, b\rbrack$ кеңістігіндегі $A = \left\{ \varphi_{p}(t) \right\}$ үйірі шала компакт жиын болу үшін, және біршенде үздіксіз болуы қажетті және жеткілікті шарттарды қанағаттандырады.

Жұмыстың мақсаты. Метрикалық кеңістіктің, сызықты нормаланған кеңістіктің және $L^{p}\lbrack a, b\rbrack$ кеңістігінің компактылығына түсінік беру және үзіліссіз функциялардың осы кеңістіктердегі жиыны жинақы болу үшін қажетті де жеткілікті шарттарды қанағаттандыратын Арцель теоремасын дәлелдеу.

Жұмыстың құрылымы . Жұмыс кіріспеден, негізгі бөлімнен, төрт тақырыпшадан, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.

1 КОМПАКТЫ ЖИЫНДАР ҰҒЫМЫ

1 Метрикалық кеңістіктегі жинақтылық

Анықтама 1. 1 Егер Х метрикалық кеңістігінде әрбір нүктелер тізбегінің шектік нүктесі болса, онда ол метрикалық кеңістік жинақы деп аталады. Әр нүктесінде жинақы шар бар метрикалық кеңістік жергілікті жинақы кеңістік деп аталады.

Бұл анықтамалардан метрикалық кеңістіктің кез келген ақырсыз ішкі жиыны да шектік нүктесін қамтыса, онда ол кеңістік жинақы болатыны шығады. Берілген анықтама тек қана шектік нүкте түсінігіне негізделгендіктен кеңістіктің жинақы болу қасиеті эквивалентті метрикаға көшкенде өзгермейді. Мысалы, $R_{1}$ нақты сандар кеңістігі $\rho_{1}(x, y) = x - y$ метрикасында да және оған эквивалентті метрика $\rho_{2}(x, y) = \left f(x) - f(y) \right$ (мұнда $f(x) = \frac{x}{1 + x}$ ) де жергілікті жинақы. Сонымен бірге барлық $R_{1}$ жинақы кеңістік болмайтыны айтылған, себебі $1, 2, \ldots, n, \ldots$ тізбегінің бірде-бір шектік нүктесі жоқ.

Теорема 1. 1 Кез келген жинақы кеңістік толық.

Дәлелдеу. Х жинақы кеңістігінің іргелі тізбегін $\left\{ x_{n} \right\}$ , ал оның шектік нүктесін $x_{0}$ арқылы белгілейік. Бізге осы тізбектің жинақталатынын, яғни $x_{0} = \lim_{n \rightarrow \infty}x_{n}$ екенін, көрсету жеткілікті. Берілген $\varepsilon > 0$ үшін N нөмірі табылып n, $m \geq N$ болғанды $\rho(x_{n}, x_{m}) < \frac{\varepsilon}{2}$ болады. Енді $\rho > N$ нөмірін $\rho(x_{p}, \ x_{0}) < \frac{\varepsilon}{2}$ болатындай етіп алайық. Сонда барлық $n > N$ үшін $\rho\left( x_{n}, x_{0} \right) \leq \rho\left( x_{n}, x_{p} \right) + \rho(x_{p}, x_{0}) < \varepsilon$ болады. Бұдан теореманың дәлелі шығады.

Мысалы, $R_{1} -$ дегі $\lbrack a, b\rbrack$ тұйық жиыны жинақы, ал сондықтан дәлелденген теорема бойынша толық. Ал кері тұжырым дұрыс емес; $R_{1} -$ толық, бірақ жинақы емес.

Жинақы кеңістік түсінігінен кеңірек түсініктің бірі - n-жинақы кеңістіктер түсінігі.

Анықтама 1. 2 Егер метрикалық Х кеңістігінің кез келген нүктелер тізбегінде іргелі ішкі тізбекше бар болса, онда ол кеңістікті жинақы деп атайды.

Егер қарастырылып отырған кеңістігіміз толық болса, онда іргелі тізбегіміз жинақталатын болады да, ал кеңістіктің өзі жинақы болады. Керісінше жинақы кеңістік толық болуы себепті, ол жинақы. Мысалы, түзу бойындағы $\lbrack a, b\rbrack$ интервалы жинақы кеңістік болғанымен жинақы бола алмайды.

Жалпы метрикалық кеңістіктердегі жиынның (шала) компакт болуының критерийін келтірер алдында $\varepsilon$ -тор ұғымының анықтамасын берейік.

Анықтама1. 3 Х - метрикалық кеңістік, $\varepsilon > 0$ - сан, ал A, $BϲX$ сол кеңістіктегі жиындар болсын. Егер B жиынының әрбір x нүктесі үшін a $\in A$ нүктесі табылып, $\rho(x, a) < \varepsilon\$ болса, онда A жиынын B жиынының $\varepsilon -$ торы деп атайды. Егер тор ақырлы санды элементтерден тұрса, онда оны ақырлы $\varepsilon -$ тор дейді.

Енді метрикалық кеңістіктегі жиынның компакт жиын болуының критерийін беретін теореманы дэлелдейік.

Теорема 1. 2 (Ф. Хаусдорф) . Толық метрикалық кеңістіктегі Е жиыны үшін кез-келген $\varepsilon > 0$ үшін ақырлы $\varepsilon$ -тор бар болуы Е жиыны шала компакт жиын болуының қажетті жеткілікті шарты.

Шарттың қажеттілігі. Е - (шала) компакт жиын болсын. Кез келген $\mathbf{\varepsilon} > 0$ үшін Е жиынының $\mathbf{\varepsilon}$ -тор болатын, саны ақырлы Т жиыны табылатынын дәлелдейік. Е жиынының кез-келген $x_{1}$ нүктесін алып, $\rho\left( x, x_{1} \right) > \varepsilon$ шартына сай $x \in E$ нүктесін іздейік. Егер бұл шарт орындалатын нүкте табылмаса, онда Е жиынының барлық нүктелері үшін $\rho\left( x, x_{1} \right) > \varepsilon$ теңсіздігі орындалатын болғаны. Демек, Е жиыны үшін тек $x_{1}$ нүктесі $\mathbf{\varepsilon}$ -тор болғаны. $\rho\left( x, x_{1} \right) > \varepsilon$

Ал, $\rho\left( x_{2}, x_{1} \right) > \varepsilon$ шартына сай $x_{2} \in E$ нүктесі бар болса, онда $\rho\left( x, x_{1} \right) > \varepsilon$ және $\rho\left( x_{1}, x_{2} \right) > \varepsilon$ шарттарына сай $x \in E$ нүктесін іздейміз. Егер бұл шарттар орындалатын нүкте табылмаса, онда $\left\{ x_{1}, x_{2} \right\}$ жиыны Е үшін $\mathbf{\varepsilon}$ -тор болғаны. Басқа жағдайда осы екі шартты қанағаттандыратын $x_{1}$ нүктесі табылады . . . Бұл әрекет қайсыбір k-нші ретте, $x_{1}, x_{2}, \ldots, x_{k}$ нүктелері табылғаннан кейін, тоқталады. Шынында да, егер ол шексіз созыла берсе, онда Е жиынының элементтерінен тұратын $x_{1}, x_{2}, \ldots, x_{k}, \ldots$ тізбегі пайда болар еді және мұндағы кез-келген екі элементтің арақашықтығы $\rho\left( x_{n}, x_{m} \right) > \varepsilon$ болар еді. Бірақ бұл тізбек жинақсыз және мұнда жинақты іштізбек те жоқ екені 3-анықтама алдында келтірілген мысалдағы байыптауға ұқсас дәлелденеді. Ал, бұл жағдай Е жиынының компактылылығы туралы теорема шартына қайшы. Демек, Е жиыны үшін $\mathbf{\varepsilon}$ -тор болатын $T = \left\{ x_{1}, x_{2}, \ldots, x_{k} \right\}$ ақырлы жиын табылады.

Шарттың жеткіліктілігі . Е жиынының $A \subset E$ ақырсыз ішжиынында жинақты тізбек бар екенін дәлелдейік. Шарт бойынша Е жиыны үшін ақырлы $\varepsilon$ -тор кез-келген $\mathbf{\varepsilon} > 0$ үшін табылады. Осыған сәйкес, $\mathbf{\varepsilon}$ = 1 үшін Е жиынының ақырлы $\mathbf{\varepsilon}$ -торы $T_{1} = \left\{ x_{1}, \ldots, x_{1k} \right\}$ жиыны болсын. Радиусы 1-ге тең, центрлері $x_{1k}(k = 1, \ldots, n_{1})$ нүктелерінде орналасқан $O_{t}\ (x_{1k})$ тұйық шарларының бірігуі Е жиынын толық қамтиды. Шынында да, кез-келген $x \in E$ үшін және $x_{1k}$ нүктелерінің ең болмаса біреуі үшін $\rho(x_{1k}, x) \leq 1$ , демек $x \in O_{t}(x_{1k})$ . Сонымен, $Eϲ\bigcup_{k = 1}^{n_{1}}{O_{1}(x_{1k}) }$ . А жиыны ақырсыз болғандыктан, осы шарлардың ең болмағанда бірінде оның ақырсыз бөлігі бар. Сол ішжиынды $A_{t}$ арқылы, ал оны қамтып жатқан шарды $O_{t}$ арқылы белгілейік.

Енді Е жиынының -торы $T_{2} = \left\{ x_{21}, \ldots, x_{2n_{2}} \right\}$ жиыны болсын. Радиусы 1/2-ге тең, центрлері 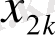нүктелерінде орналасқан 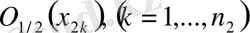тұйық шарларының бірігуі Е жиынын толық қамтиды. Осы шарлардың ең болмаса бірінің $A_{1}$ жиынымен қиылысуы $A_{2}$ - ақырсыз жиыны болады. Оны қамтып жатқан шарларды арқылы белгілейік. Сонда, $A_{2} \subset O_{2} \subset O_{1}$ . Осы әрекетті әрі қарай шексіз қайталау нәтижесінде $O_{1} \supset \ldots \supset O_{k} \supset \ldots$ тұйық шарлар тізбегі, сонымен қатар $A_{1} \supset \ldots \supset A_{k} \supset \ldots$ ақырсыз жиындар тізбегіпайда болады. Мұнда $A_{k} \subset O_{k}$ және $O_{k}$ шарының радиусы $\frac{1}{k}\ (k = 1, 2, \ldots)$ . Біріне бірі еніп жатқан тұйық шарлар тізбегі туралы теорема бойынша осы шарлардың бәріне тиісті бір ғана 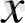нүктесі бар, яғни 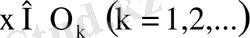. . Енді әр $A_{k}$ жиынынан бір $x_{k}$ нүктесін алайық. Онда $x_{k} \in A_{k}\ \subset O_{k}$ демек, $\rho(x, x_{k}) \leq \frac{2}{k}$ , яғни $\left\{ x_{k} \right\}$ тізбегі $k \rightarrow \infty$ кезде x нүктесіне жинақталады. Ақырында, $x_{k} \in A_{k}\ \subset A$ , демек кез-келгенA ⊂ E ақырсыз жиынында жинақты тізбек бар екені айқындалды.

Осымен теорема толық дәлелденді.

Ескерту. Егер Е жиыны үшін кез-келген $\varepsilon > 0$ санына сәйкес ақырлы $\varepsilon$ -тор бар болса, онда Е жиыны, әдетте, жете шенелген жиын деп аталады.

Ақырлыn өлшемді $R^{n}$ Евклид кеңістіктеріндегі шенелген тұйық жиындар үшін Больцано - Вейерштрасс теоремасы мен Гейне - Борель леммасында берілетін қасиеттер бір біріне эквивалентті. Бұл эквиваленттілік метрикалық кеңістіктерде (ақырсыз өлшемді болса) компакты жиындар үшін де сақталады. Бұдан компакты жиындар сандар кеңістігіндегі шенелген тұйық жиындардың қасиеттерін жалғастыратынын көреміз.

Анықтама 1. 4 $\left\{ G_{\xi} \right\}$ ашық жиындар жүйесі $M \subset X$ жиынының ашық бүркеуі дейміз, егер әрбір $x \in M$ нүктесі осы жүйенің кемінде бір $G_{\xi}$ жиынына тиісті болса, яғни $M \subset \ \bigcup_{\xi}^{}G_{\xi}$ болса.

Теорема 1. 3 $M \subset X$ жиыны компакты болу үшін оның кез келген $\left\{ G_{\xi} \right\}$ ашық бүркеуінен ақырлы ішбүркеу бөлінетін болуы қажет және жеткілікті.

Дәлелдеуі. Қажеттігі. М компакты жиынымен оның кез келгенN = $\left\{ G_{\xi} \right\}$ ашық бүркеуі берілсін. Онда кез келген $\varepsilon > 0$ үшін М жиынына ақырлы $\varepsilon$ - тор $\left\{ x_{1}, x_{2}, \ldots, x_{n} \right\}$ табылады. Әрбір $x \in M$ үшін $\rho\left( x_{1}, x_{2} \right) < \varepsilon\ (k = 1, 2, \ldots, n)$ теңсіздіктерінің кемінде біреуі орындалады, сондықтан $M \subset \ \bigcup_{k = 1}^{n}{S_{k}\ (x_{k}, \varepsilon) }$ . Егер берілген $\varepsilon > 0$ үшін $S_{k}\ (x_{k}, \varepsilon)$ шарларының әрқайсысы кемінде бір $G_{\xi k} \in N$ жиынында жатса, онда $M \subset \ \bigcup_{k = 1}^{n}G_{\xi k}$ . Бұл ақырлы бүркеу бөлінгені. Осындай $\varepsilon > 0$ табылатынын көрсету керек. Ол үшін, қандай $x \in M$ алсақ та $S\ (x, \varepsilon)$ шары бір $G_{\xi}$ жиынында түгел жататындай $\varepsilon > 0$ табылатынын дәлелдейік. Олай болмаса, $\varepsilon_{n} \rightarrow 0\ (n \rightarrow \infty)$ және $\in M$ тізбектері табылып $S\ (x_{n}', \varepsilon_{n})$ шарлары ешбір $G_{\xi k} \in N$ жиынында жатпайды. М компакты болғандықтан $\left\{ x_{n}' \right\}$ тізбегінен бір $x_{0} \in M$ нүктесіне жинақталатын $\left\{ x_{n_{k}}' \right\}$ іштізбегі бөлінеді. Осы x ₀ нүктесін қамтитын $G_{\xi 0} \in N$ жиын бар, $G_{\xi 0}$ ашық болғандықтан ол x ₀ нүктесін бір $\delta$ - маңайымен бірге қамтиды $S\ (x_{0}, \delta) \subset G_{\xi 0}$ . Онда $\xi_{n_{k}} < \frac{\delta}{2}$ болатын жеткілікті үлкен $n_{k}$ үшін: $\rho\left( x_{n}', x_{0} \right) < \xi_{n_{k}} < \frac{\delta}{2}$ . Сондықтан $S\ (x_{n_{k}}', \varepsilon_{n_{k}}) \subset \ S\ (x_{0}, \delta) \subset G_{\xi 0}$ . Алуымыз бойынша $S\ \left( x_{n_{k}}', \varepsilon_{n_{k}} \right)$ шары ешбір $G_{\xi k} \in N$ жиынында жатпайды. Қайшылық керек $\varepsilon > 0$ бар екенін дәлелдейді.

Жеткіліктілігі. М жиынының кез келген ашық бүркеуінен ашық ішбүркеу бөлінетін болсын. Шектік нүктесі жоқ $N \subset M$ ішжиын бар дейік. Онда әрбір $x \in M$ нүктесінің қайсыбір $S\ (x, \varepsilon_{x})$ маңайында N- нің осы x- тан басқа нүктесі болмайды $\left\{ S\ \left( x, \varepsilon_{x} \right) - x \right\} \cap N = \varnothing$ және $M \subset \ \bigcup_{x \in M}^{}{S\ \left( x, \varepsilon_{x} \right) }$ . Шарт бойынша М-ді бүркейтін саны ақырлы $S\ \left( x_{1}, \varepsilon_{1} \right), \ldots, S\ \left( x_{n}, \varepsilon_{n} \right)$ шарлар бөлінеді. Бұл шарлардың әрқайсысында N - нің бір ғана нүктесі болуы мүмкін, яғни N- ақырлы жиын. Онда М - нің әрбір ақырсыз бөлігінің шектік нүктесі бар, яғни М азкомпакты. Енді М - нің тұйық екенін көрсету жеткілікті. Егер әрбір $x_{0} \notin M$ шектік нүкте болмайтынын көрсетсек, онда М- нің шектік нүктелері өзінде жататынын, яғни оның тұйық жиын екенін аламыз. Әрбір $x_{0} \notin M$ және кез келген $x \in M$ үшін. Ашық шарлар $S\left( x_{0}, \frac{r_{x}}{3} \right), S(x, \frac{r_{x}}{3})$ қиылыспайды және $\ M \subset \ \bigcup_{x \in M}^{}{S\ \left( x, \frac{r_{x}}{3} \right) }$ . Шарт бойынша $\left\{ S\left( x, \frac{r_{x}}{3} \right) \right\}$ ашық бүркеуден ақырлы $S\left( x_{1}, \frac{r_{x_{1}}}{3} \right), \ldots, S(x_{n}, \frac{r_{x_{n}}}{3})$ ішбүркеу бөлінеді. Енді $r_{0} = \min_{k}r_{x_{k}}$ десек, онда $S\left( x_{0}, \frac{r_{0}}{3} \right)$ шары $S\left( x_{k}, \frac{r_{k}}{3} \right), \ (k = 1, 2, \ldots, n)$ , шарларының ешқайсысымен де, сондықтан М - мен де қиылыспайды. Сондықтан, $x_{0} \notin M$ нүктесі M үшін шектік нүкте емес.

Дәлелденді .

Метрикалық кеңістіктердегі компакты жиындар

Қандай жиыннан жинақты тізбек бөлінетінін білу анализдегі негізгі мәселелердің бірі, оны математикалық анализдегі Гейне - Борель леммасының немесе Больцано - Вейерштрасс теоремасының алатын орнымен түсіндіруге болады.

Анықтама 1. 5 Х метрикалық кеңістігінің М жиыны компакты жиын дейміз, егер оның әрбір ақырсыз бөлігінен (ішжиынынан) осы М жиынының өзінің бір нүктесіне жинақталатын іштізбек бөлінетін болса.

Жинақты тізбек пен оның кез келген іштізбегінің шегі біреу екенін білеміз. Бұдан компакты жиынның тұйық болатынын көреміз және компакты жиынның тұйық ішжиыны да компакты болатынын түсінікті.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.