Метрикалық кеңістіктегі ашық және тұйық жиындар

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 10 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ5

1 МЕТРИКАЛЫҚ КЕҢІСТІК6

1. 1 Метрикалық кеңістік ұғымы8

1. 2 Метрикалық кеңістіктегі жинақтылық8

1. 3 Метрикалық кеңістіктегі ашық және тұйық жиындар9

2. ЖИНАҚТЫЛЫҚ11

2. 1 Жинақтылық ұғымы12

2. 2 Функционалдар мен элементтердің әлсіз жинақтылығы12

ҚОРЫТЫНДЫ. 16

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ17

КІРІСПЕ

Жұмыстың өзектілігі: Математикалық анализдегі ең негізгі ұғымдардың бірі бұл шек және үзіліссіздік ұғымы. Бұл ұғымдарды анықтау үшін түзудің, жазықтықтың, кеңістіктің бойындағы екі нүктенің арақашықтығы ұғымын білу керек. «Арақашықтық» ұғымының мағынасы элементар үш аксиома (тепе-теңдік, симметриялық және үшбұрыш теңсіздігі) арқылы жақсы түсіндіріледі. «Арақашықтық» ұғымын жалпылау арқылы метрика ұғымына, сосын метрикалық кеңістік ұғымына келеміз. Метрика ұғымы тізбектердің, қатарлардың жинақталуын зерттеуге және функцияның үзіліссіздігін, дифференциалдануын зерттеуге көмектеседі.

Жұмыстың қысқаша құрылымы: «Метрикалық кеңістік» тақырыбында жазылған. Курстық жұмыс үш бөлімнен тұрады: кіріспе, негізгі бөлім, қорытынды.

«Метрикалық кеңістік анықтамасы және оған мысалдар» бөлімінде метрикалық кеңістіктің аксиомалары, метрикалық кеңістікке мысалдар келтірілген.

«Метрикалық кеңістіктегі жинақтылық» бөлімінде метрикалық кеңістікте жинақтылықты қалай енгізуге болатындығы туралы анықтамалар келтірілген.

«Метрикалық кеңістіктегі ашық және тұйық жиындар» бөлімінде жиынның ішкі, сыртқы және шекаралық нүктелерінің анықтамасы мысалдармен қарастырылған.

Жұмыстың мақсаты. Метрикалық кеңістіктің анықтамасын, метрикалық кеңістікте жинақтылықты қалай енгізетіндігі түсінік беріп, оларды мысалдар арқылы көрсету.

Метрикалық кеңістік

Метрикалық кеңістік ұғымы

$E$ - кез келген бос емес жиын болсын.

Анықтама 1 . Егер $E$ жиынының кез келген х, у элементтерінің жұбына теріс емес нақты $\rho_{E}$ $(x, y)$ саны сәйкес қойылса және төмендегі шарттарды

1. $\rho_{E}(x, y)$ $\geq$ 0; $\rho_{E}(x, y)$ $=$ 0 $< = >$ $x$ = $y$ (тепе-теңдік аксиомасы) ;

2. $\rho_{E}(x, y)$ $=$ $\rho_{E}(y, x)$ (симметрия аксиомасы) ;

3. $(\forall x, \ y, \ z\ \in E\ )$ : $\rho_{E}$ $(x, y)$ $\leq$ $\rho_{E}$ $(x, z)$ $+$ $\rho_{E}$ $(z, y)$ (үшбұрыш аксиомасы) қанағаттандыратын болса, онда $\rho_{E}(x, y)$ санын $E$ жиынының $x, y$ элементтерінің ара қашықтығы немесе $E$ жиынының метрикасы және жоғарыдағы көрсетілген 1) -3) шарттарды метриканың аксиомалары деп атайды. Ал $E$ жиыны мен осы жиында анықталған $\rho_{E}(x, y)$ жұбын $E$ метрикалық кеңістігі деп атайды.

Алда $E$ кеңістігі нақты кеңістік болған жағдайда $\rho_{E}(x, y)$ - тің орнына деп жазамыз.

Метрикалық кеңістіктердің жиі кездесетін мысалдары:

EE=RR- Евклид түзуі (нақты сандар жиыны) . (−∞; +∞) ( - \infty; + \infty) сан өсіндегі ара қашықтығын

$\rho(x, y)$ = $x - y$

Түрінде анықтауға болады. $\rho(x, y)$ метриканың барлық аксиомаларын қанағаттандырады. Шынында

ρ(x, y) \rho(x, y) =x−y≥0x - y \geq 0; ρ(x, y) \rho(x, y) = 0<=>< = >x−y=0x - y = 0<=>< = >x=yx = y;
ρ(x, y) \rho(x, y) =x−y=x - y =(−1) (y−x) \left ( - 1) (y - x) \right=y−xy - x=ρ(y, x) \rho(y, x) ;
(∀x, y, z∈R) (\forall x, \ y, \ z\ \in R\ ) :ρ(x, y) \rho(x, y) =x−y=x - y =x−z+z−yx - z + z - y≤\leqx−zx - z++z−yz - y=ρ(x, z) \rho(x, z) ++ρ(z, y) \rho(z, y) .

Сондықтан $R$ кеңістігі - метрикалық кеңістік.

Евклид жазықтығыEE=R2R^{2}болсын. A1(x1, y1) A_{1}\left( x_{1}, \ y_{1} \right) жәнеA2(x2, y2) ∈EA_{2}\left( x_{2}, \ y_{2} \right) \in E

нүктелерінің ара қашықтығын

$\rho\left( A_{1}, \ A_{2} \right)$ = $\sqrt{\left( x_{2} - x_{1} \right) ^{2} + \left( y_{2} - y_{1} \right) ^{2}}$

түрінде анықтауға болады. $\rho\left( A_{1}, \ A_{2} \right)$ метриканың барлық аксиомаларын қанағаттандыратынын оңай көрсетуге болады. $R^{2}$ жазықтығымен $\rho\left( A_{1}, \ A_{2} \right)$ метрикасының жұбын екі өлшемді евклид кеңістігі деп атайды.

Дәл осы сияқты координаталары реттелген нақты сандардан тұратын нүктелер жиыны

$\rho\left( A_{1}, \ A_{2} \right)$ = $\sqrt{\sum_{i = 1}^{n}\left( x_{i} - y_{i} \right) ^{2}}$ , ( $A_{1}\ \left( x_{1}, \ x_{2}, \ \ldots, \ x_{n} \right)$ , $A_{2}\ \left( y_{1}, \ y_{2}, \ \ldots, \ y_{n} \right)$ )

метрикасы арқылы $n$ - өлшемді Евклид кеңістігін анықтайды.

Метрикалық кеңістіктерде үшбұрыш аксиомасының орындалатынын тексергенде жиі қолданылатын теңсіздіктер:

1. Коши-Буняковский теңсіздігі:

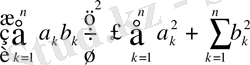және оның салдары:

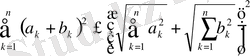2. Гельдер теңсіздігі:

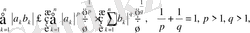
1. 2 Метрикалық кеңістіктегі жинақтылық

$E$ метрикалық кеңістігінің элементтерінен тұратын $\left\{ x_{n} \right\}$ тізбегін қарастырайық.

Анықтама 2. $E$ метрикалық кеңістігінің $x$ элементін $\left\{ x_{n} \right\}$ тізбегінің шегі деп атайды, егер

$(\forall\varepsilon > 0)$ $\left( \exists N(\varepsilon) \right)$ $\left( \forall n:n > \left\lbrack N(\varepsilon) \right\rbrack \right)$ : $\rho_{E}\left( x_{n}, x \right) < \varepsilon$

болса, және оны қысқаша былай белгілейді:

$\lim_{n \rightarrow \infty}x_{n} = x$

Егер $\left\{ x_{n} \right\}$ тізбегінің $n \rightarrow \infty$ кезде шегі бар болса, онда оны осы метрикалық кеңістіктің анықтамасы бойынша $x \in E$ нүктесіне жинақталатын тізбек дейді. Ал егер $\left\{ x_{n} \right\}$ тізбегі $E$ метрикалық кеңістігінің ешбір нүктесіне жинақталмайтын болса, онда оны жинақталмайтын тізбек деп атайды.

Кез келген метрикалық кеңістіктегі шек анықтамасын сандық тізбектің шегі туралы анықтамаға келтіруге болады.

Анықтама 3. $E$ метрикалық кеңістігінің $x$ элементін $\left\{ x_{n} \right\}$ тізбегінің шегі деп атайды, егер $\rho_{E}\left( x_{n}, x \right)$ сандық тізбегі $n \rightarrow \infty$ кезде нөлге ұмтылатын болса, яғни

$\lim_{n \rightarrow \infty}{\rho_{E}\left( x_{n}, x \right) } = 0$

Мысал. $C\ L_{1}\lbrack 0, 1\rbrack$ кеңістігінен алынған $\left\{ x_{n}(t) = t^{n} \right\}$ функционалдық тізбегінің шегі $\theta(t) \equiv 0$ функциясына жинақталатынын көрсетіңдер.

Шынында да, бұл кеңістікте

$\rho_{E}\left( x_{n}, \theta \right) = \int_{0}^{1}{\left x_{n}(t) - \theta(t) \rightdt} = \int_{0}^{1}{t^{n}dt} = \frac{1}{n + 1}$

Сондықтан,

$\lim_{n \rightarrow \infty}{\rho_{CL}\left( x_{n}, \theta \right) } = \lim_{n \rightarrow \infty}{\frac{1}{n + 1} = 0}$

Олай болса, 3 анықтама бойынша $\left\{ t^{n} \right\}$ тізбегі $C\ L_{1}\lbrack 0, 1\rbrack$ кеңістігінде жинақталатын тізбек және $\theta(t) \equiv 0$ функциясы оның шегі болып табылады.

Бірақ бұл тізбек $C\ \lbrack 0, 1\rbrack$ кеңістігінде $\theta(t) \equiv 0$ функциясына жинақталмайды, өйткені

$\lim_{n \rightarrow \infty}{\rho_{C}\left( x_{n}, \theta \right) } = \lim_{n \rightarrow \infty}{\max\left t^{n} \right = \lim_{n \rightarrow \infty}{1 - 1 \nrightarrow 0}}.$

1. 3 Метрикалық кеңістіктегі ашық және тұйық жиындар

$\alpha$ - жазықтығында берілген $X$ жиынын қарастырайық. Осы $\alpha$ жазықтығының барлық нүктелері $X$ жиынына қатысты 3 класқа бөлінеді. Мысалы, $\alpha$ нүктесі - ішкі, $b$ нүктесі - сыртқы, $c$ нүктесі шекаралық нүкте болады.

Дәл осылай сияқты метрикалық кеңістіктің кез келген ішкі жиынына қатысты оның кез келген нүктелерін классификациялауға болады.

$X$ жиыны $E$ метрикалық кеңістігінің қандай да бір ішкі жиыны болсын, яғни $X$ $\subset$ $E$ .

Анықтама 4. $E$ метрикалық кеңістігінің $a$ нүктесін $X$ жиыны үшін ішкі нүкте деп атайды, егер ол өзінің қандай да бір маңайымен осы $X$ жиынында толығымен жататын болса, яғни

$\left( \exists S_{1}(a) \right)$ : $S_{2}(a)$ $\subset$ $X$ .

Анықтама 5. $E$ метрикалық кеңістігінің $b$ нүктесін $X$ жиыны үшін сыртқы нүкте деп атайды, егерде оның $X$ жиынымен қиылысуы бос болатын қандай да бір $\varepsilon$ маңайы табылатын болса, яғни

$\left( \exists S_{\varepsilon}(b) \right)$ : $S_{\varepsilon}(b)$ $\cap$ $X$ = $\varnothing$ .

Анықтама 6. $E$ метрикалық кеңістігінің $c$ нүктесін $X$ жиыны үшін шекаралық нүкте деп атайды, егерде $c$ нүктесінің кез келген $\varepsilon$ маңайында $X$ жиынында жататын да, жатпайтын да нүктелер табылатын болса. $X$ жиынының барлық шекаралық нүктелер жиынын $X$ жиынының шекарасы деп атайды және $\partial X$ деп белгілейді.

Осы анықтамалардан мынандай қорытынды жасауға болады: $E$ метрикалық кеңістігінің кез келген нүктесі $X$ жиыны үшін не сыртқы, не ішкі, не шекаралық нүкте болады. Сонымен қатар, $X$ жиынының барлық ішкі нүктелері $X$ жиынында жатады, ал сыртқы нүктелері жатпайды. Шекаралық нүктелері өзінде жатуы да, жатпауы да мүмкін.