ПЕРИОДТЫҚ СИГНАЛДЫҢ ЭНЕРГИЯСЫНЫҢ СПЕКТРДЕ ТАРАЛУЫ

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Лекция - 5 - 6 . 15. 02. 2005. ж. 22. 02. 2005. ж.

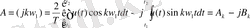(1. 19)

мұнда

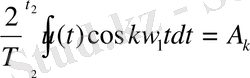(1. 20)

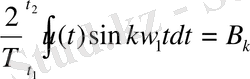(1. 21)

Амплитуда спектрі 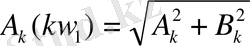(1. 22)

К функциясының жұп функциясы болып табылады, яғни

(1. 23)

А _к және В _к жұптылығы бір - біріне қарама - қарсы болғандықтан, фаза спектрі келесі түрде болады:

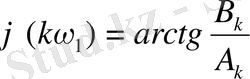- тақ функция, яғни 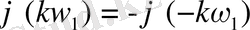(1. 24)

егер к=0 болса, тұрақты құрамдас бөліктері келесі түрде болады.

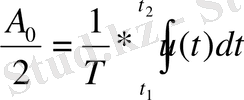(1. 25)

Екі жақты спектрлі көрсетуден бір жақты көрсетуге кешенді түйіндес біріктіру арқылы (1. 14 - формула) көшуге болады. Бұл жағдайда Фурье кашарын тригоноиетриялық түрде аламыз. (1. 15) өрнегінен А ₀ /2 тұрақты құрамдас бөліктерін бөлектеп, ώ және - ώ симметриялық жиіліктердің құрамдас бөліктерін қосып, төмендегі өрнекті аламыз.

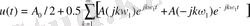(1. 26)

(1. 15) және (1. 16) өрнектерін ескере отырып, келесі өрнекті аламыз:

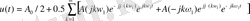
немесе

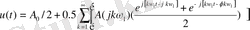
Эйлор формуласын пайдаланып және φ(кώ1) = φкдеп белгілеп, төмендегідей формуланы аламыз:

(1. 27)

Фурье кашарының басқа да тригонометрилық түрлері де бар.

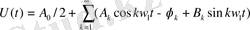(1. 28)

(1. 23) және (1. 24) өрнектеріндегі жеке құрамдас бөліктер гармоникалар деп аталады.

ПЕРИОДТЫҚ СИГНАЛДЫҢ ЭНЕРГИЯСЫНЫҢ СПЕКТРДЕ ТАРАЛУЫ

U(t) күрделі периодтық сигналдың оның спектрлі құрамдас бөліктері ьойынша энергияның таралуын қарастырамыз. U(t) уақытша функциясы деп резистордегі 1Ом электр кернеуін қарастырамыз. W _T - энергиясы Т - тербеліс периодына тең уақыт аралығында осы резисторда төмендегідей өрнектеледі.

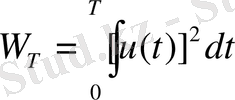(1. 34)

W _T Фурье катары түріндегі спектрлі көрсетілуін қолданып келесі өрнекті аламыз.

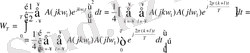(1. 35)

(1. 35) өрнегінің мәндерін анықтаймыз.

(1. 36)

A(jkw ₁ ) және A(-jkw ₁ ) комплексті түйіндес болғандықтан

A(jkw ₁ ) *A(-jkw ₁ ) =[A(jkw ₁ ) ] ² (1. 37)

(1. 28) және (1. 29) өрнектерін ескерсек W _T - ны келесідей жазуға болады:

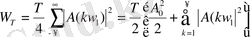(1. 38)

(1. 38) - ден келесі салдары: күрделі периодтың сигналдың энергиясының қосындысына тең. Энергияның резисторы 1 Ом әрбір оның гатмоникасы жекеше бөлінетін (тұрақты құрамдас, бөліктерін есептегенде) уақыт өте бөлінетін энергия, бірақ орташа қуат тұрақты болады.

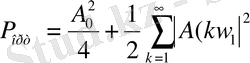(1. 39)

ПЕРИОДТЫ ЕМЕС СИГНАЛДАРДЫҢ СПЕКТРІ

Кез - келген физикалық түрде іске асатын сигнал уақыт бойынша шектелген және соңғы энергиясы бар нақты сигналды сипаттайтын Дирихле шартын қанағаттандыратын функция абсольюттік интегралданады:

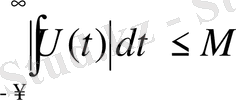(1. 40)

мұнда М - соңғы шама

U(t) - оңашаланған импуль спектрі

Көрсетуін U ₁ (t) коэффициент сигналының периодының шексіздікке дейін артуының салдарынан аламыз U ₁ (t) периодтың функциясы үшін Фурье түрлендіруі (1. 15 және 1. 16) өрнектерін қосып төмендегідей қосамыз.

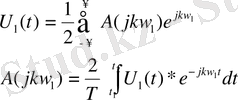
Егер Т=≥∞ U ₁ (t) - ны U(t) - ға ауысады, онда w ₁ жиілігі dw - ға дейін кемиді. Ал kw ₁ ағымдағы w - жиілігіне айналады. Қосындыны интегралмен алмастырып төмендегідей өрнекті аламыз.

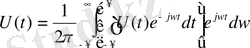
интегралды квадраттық жақшалар S(jw) арқылы белгілеп тікелей және кері интгралданған Фурье түрлендіру үшін келесі формуланы аламыз.

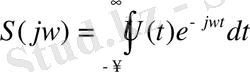(1. 41)

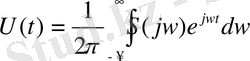(1. 42)

S(jw) - шамасын комплексті спектрлі тығыздық немесе спектрлі мінездеме деп атайды. өлшембірлігі жиілік амплитуда. әрбір нақты жиілікте сәйкес құрамдас бөліктерінің амплитудасы 0 -ге тең. (1. 15) және (1. 42) - өрнектерін салыстыра келіп dw шексіз кіші комплекстік амплитуда сәйкес келетін анықтаймыз.

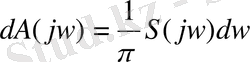(1. 43)

(1. 41) өрнегін t ₁ ≤t≤t ₂ уақыт аралығында берілген U(t) функциясының спектрі мінездемесін (1. 17) формуласымен салыстыра келе нақ осындай функцияның комлексті спектрінің қисығына арналған (ол периодты түрде уақыт бойынша жалғасады) Олар тек көбейтіндісімен ғана ерекшеленеді.

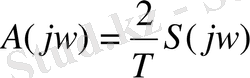(1. 44)

Сондықтанда жекешеленген импульстің спектрлі мінездемесі арқылы периодтың тізбектегі сызықтық спектрді құрастыруға болады. Ал спектрлі мінездеменің комплексті шамасы келесі түрде болады.

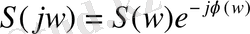(1. 45)

мұнда S(w) =[S(jw) ] амплитуданың спектрлі тығыздығы немесе преиодты емес сигналдың спектрі деп аталынады. Құрамдас бөліктері барлық жиілікте орналасқандықтан периодты емес сигналдың спектрі үздіксіз немесе тұтас болады. Нақты және жалған бөлшектердей тұратын спектрлі мінездемелері төмендегідей болады.

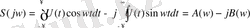(1. 46)

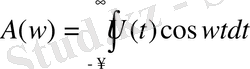(1. 47)

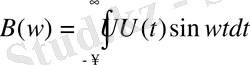(1. 48)

S(w) спектрлі мінездеменің модулі келесі өрнекпен анықталады:

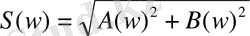(1. 49)

және жиіліктің жұп функциясы болып табылады. (1. 42) және (1. 43) өрнектерінен шығатын салдар:

A(w) - жиіліктің жұп функциясы, онда φ(ώ)

B(w) - жиіліктің тақ функциясы, функциясы жиілікке қатысты тақ болады. Ал Фурье интегралды түрленуінің тригонометриялық формасы келесідей:

(1. 50)

Интеграл астындағы өрнек тақ болғандықтан екінші мүшесі 0 - ге тең болады да келесі өрнекті аламыз:

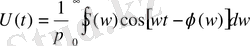(1. 51)

ПЕРИОДТЫ ЕМЕС СИГНАЛДЫҢ ЭНЕРГИЯСЫНЫҢ СПЕКТРНДЕ ТАРАЛУЫ

U(t) - периодты емес сигналдың физикалық сипатталынуы электрлік кернеу, оның кедергісі 1Ом. Онда резисторде бөлінетін энергия төмендегідей:

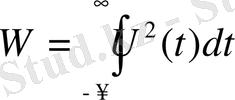(1. 54)

(1. 54) интеграл сәйкес келеді деп есептейміз, энергияны U(t) сигналының S(w) спектрлі мінездеменің модулі арқылы өрнектейміз, осы модульдің квадраты келесі түрде болады.

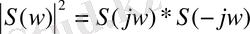(1. 55)

мұнда

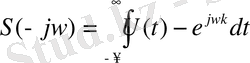- функция

Ол U(t) сигналының S(jw) спектрлі мінездемесіне комплексті түтіндес болып келеді. Онда:

Интегралдау тәртібі өзгергеннен кейін және Фурьенің кері түрлендіруін (1. 42) өрнегін пайдаланып келесі өрнекті аламыз:

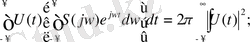
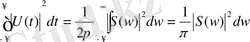(1. 56)

(1. 56) өрнегі «Парсеваль» теңдігі деп аталады.

Апаратты кодтау. Кодтау теориясының жалпы түсініктері. Анологты түрлендіргіштер.

Керек дискретті хабарлама немесе хабарлама белгісінқандай да бір реттік нөмірімен белгілеуге болады. Аналогтық шаманы өңдеу оны үлгідей өлшеммен салыстыруын сипаттайды. Ол да ақпаратты сандық көрсетуге алып келеді. Бұл жағдайда ақпаратты тарату немесе сақтау, сандық тарату немесе сақтауға алып келеді. Сандарды кандай да бір есептеу жүйеде өрнектеуге болады. Осылайша осы есептеу жүйесіне негізделген кодтаудың біреуі алынады. Қазіргі кезде есептеу жүйесін құрудың позициялық принципі жалпыға танылған, әрбір символдың мәні, оның орналасқан орнына байланысты, яғни санды көрсететін символдар қатарындағы орнына байланысты. Әрбір келесі разрядтың бірлігі алдыңғы разрядтағы бірліктен m есе үлкен. Мұнда m - есептеу жүйесінің негізі. Разрядтар бойынша мәндерді қосу арқылы толық санды аламыз:

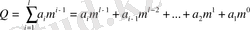
мұндағы і - осы санның разрядының нөмірі l - разрядтар саны.

a _i - 0 және l -1 аралығындағы керек бүтін санды қабылдайтын көбейткіш, ол санда і - ші разрядтағы қанша бірлік бар екенін көрсетеді. Есептеу жүйесінің негізгі соғұрлым үлкен болған сайын, сол санды көрсету үшін анағұрлым аз разрядтар саны қажет болады. Сәйкесінше оны тарату үшін аз уақыт қажет етеді, бірақ негіздің өсуіне байланысты әртүрлі символдарға сәйкес келетін қарапайым символдары құрастыратын және шашатын апаратураға немесе байланыс желісіне талаптар жоғарлайды. Бұл жағдайда құрылғылардың есептеудің логикалық элементтерінің тұрақты жағдайының саны көп болу керек. m жағдайды да ескере отырып, керек санды өрнектеу үшін әртүрлі символдардың санын m разрядтар санына l миниммум көбейтіндісін қамтамасыз ететін жүйені . Бұл минимумды 5. 1 суреттегі график бойынша табамыз. Мұнда нақты жеткілікті үлкен санды Q(Q ≈ 6) көрсеткенде m және l шамалары арасындағы байланыс көрсетілген.

m m L m x l

1 6 6

2 16 32

3 10 30 4 8 32

16 4 64

40 3 120

3 6 1 6

Графикпен көретініміз ең тиімді жүйе үштік жүйе. Екілік және төрттік жүйеде одан сәл орын береді. Негіздері 10 және одан да басқалары аз тиімді. Осы жүйелерді арифметикалық және лгоикалық амалдардың орындалуының қарапайымдылығына байланысты сәйкесінше лгоикалық элементтерінің физикалық іске асуын салыстыра келе 2 - лік жүйе таңдаймыз. 2 - лік жүйеде логикалық элементтердің 2 тұрақты жағдайы болу қажет. 2 - лік жүйеде арифметикалық және логикалық амалдар төмендегідей орындалады.

Қосу ережесі:

0+0=0

1+0=1

0+1=1

1+1=10

Азайту ережесі:

1-0=1

10-1=1

0-0=0

1-1=0

Көбейту ережесі:

1*0=0

1*1=1

0*1=0

0*0=0

Кодтау және декодтауға қолданылатын логикалық операция модуль бойынша қосу 2 - лік жүйеде келесі теңдікпен анықталады:

Екілік жүйеден 10 - қ жүйеге өту алгоритмі келесідей; үлкен разрядтан есептейміз. Егер келесі бөлімде 0 тұрса, онда алдындағы (жоғары) разряд екіленеді. Егер келесі разрядта 1 болса, онда алдындағы разряд 2 еселенгеннен кейін нәтижеге 1 санын қосамыз.

1001

1*2=2

2*2=4

4*2=8+1=9

1101

1*2=2+1=3*2=6*2+1=13

1011

1*2+2*2+1=5*2+1=11

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.