Ұғым— логакалық категория

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

Ұғым— логакалық категория. Ұғымның негізгі мінездемелері
Педагогика ғылымы ғылыми ұғымдарды олардың таным процесіңцегі
гаосеологиялық жене психологиялық маңызына сүйене отырып, білім мазмұнының
басты қүрьшымдық бірлігі ретіңде анықтайды. ұғым шыңдық дүниесін біржақты
ғана бейнелемейді, объектілердің жалпы маңызын ашып көрсетеді, заттың
елеулі қасиеттерін анықтаумен қатар, жалпы мен жалқының, нақты
менГабстрактінің бірлігін, белгілі бір ғылым саласының даму нәтижесін, оның
көп уақыт тырнақталып жиналған қорытындысын түйіндейді.
Ұғым қарастыратын объектінің, құбылыстың соған ғана тән ерекше қасиетін
сипаттайды.
Мысалы: 1) Адам сөйлей алатын омыртқалылар тобының мүшесі;
2) радиус — шеңбер центрін оның бойыңдағы кез келген нүктемен қосатын
кесінді.
ұғым — зерттелінетін объектінің жалпы, сонымен бірге маңызды белгілері,
негізгі ой түйіні болатын барлық айрықша сипаттары туралы түсінік,
мәліметтердің түтастай жиынтығы туралы пайымдар.
Ұғым - ете күрделі логикалық жөне гносеологиялық категория. Ол
біріншіден, жоғарғы материяның жемісі; екіншіден, ол шындық дүниесін
бейнелейді; үшіншіден, жалпылау құралы; төртіншіден, ұғымның қалыптасуы
сөзбен, жазумен және белгілеумен тығыз байланысты болады. Сонымен ұғым —
ойлаудың жоғарғы түрі, шындық дүниесін сипаттайтын "қару" болып табылады.
Оқыту процесіңде математикалық ұғымдардың пайда болуы мен құрылымы,
олардың материалдық дүниенің заттарымен, құбылыстарымен байланысьш ашу —
мүғалімнің бірден бір міндеті. Мүғалім бұл күрделі әдіснамалық мәселені
шешу нәтижесінде оқушылардың ғылыми дүниетанымын қалыптастырады. Математика
ақиқат (шындық) дүниенің белгілі бір жағы болып табылатын мөлшерлік
қатынастар
және кеңістіктік формалар, абстрактілі объектілер мен олар туралы
ұғымдарды зерттейтін ғылым екендігін түсінуге мүмкіндік береді.
Кез келген ұғым, оның ішінде математикалық ұғым да, табиғатта бар
заттардың елеулі белгілерін абстракциялау арқылы пайда болады. Бірақ
математикалық ұғымдар заттар мен құбылыстардың нақтылы мазмұнын елемей,
олардың барлығына ортақ мелшерлік қатынастар мен формаларды ғана
бейнелейді. Академик Ә. Нысанбаевтың [154] сөзімен айтқанда "математика
заттардың өзін емес, сол заттардың бейнесі болатын белгілерін және
абстрактілі құрылымы мен функцияларын зерттейді". Математика абстрактілі
объектілермен тікелей қатынаста болады. Бірақ материадцық объекті мен
математикалық объектіні шатастырмау қажет. Математикалық объекгі
материалдық объектінің дәл өзі емес, оның күрделі абстракция нәтижесінде
пайда болатын көшірмесі, бейнесі, яғни абстрактілі объект (нүкте, түзу,
сан, жиын, топ, функция, оператор, құрылым т.б.). Айталық, бөлмедегі
орыңдықтардың санын есептейтін болсақ, біз олардың түсіне, сапасына көңіл
аудармаймыз, санына ғана көңіл аударамыз. Қанша адамға орындық керек,
қаншасы бар, қаншасы жоқ, жетпейтіні қанша? — соны білуге үмты-ламыз. Басқа
заттарды санағанда да олардың физикалық қасиетіне назар аудармай тек
олардың санын білуге тырысамыз. Сондай-ақ қандай да бір ыдыстың сыйымдылы-
ғын анықтау қажет болса, ол ыдыстың қандай материалдан жасалғанына мән
бермей, оның пішінін ғана ескереміз. Екі қаланың ара қашықтығьш есептегенде
қалаларды нүкте, керулі түрған жіпті түзу сызық ретінде қарастырамыз.
Жіптің жуаңдығы немесе оның қаңдай материалдан ширатьглғаңдығы
ескерілмейді. Осылайша абстракциялау нәтижесінде математикалық ұғымдар
пайда болады.
Математикалық ұғымдар пайда болатын абстракцияның бір түрі —
идеализация абстракциясы. Өлшемі жоқ нүкте, қалындығы жоқ сызық т.б.
алғашқы геометриялық ұғымдар абстракцияның осы түрі негізіңце келіп шыққан.
Жер бетінде әр жаққа тартылған жіп немесе сым темір, дәптер бетіңдегі
сызық, тағы басқаларды біз бір класқа біріктіріп қана қоймаймыз, санамызда
идеалды "сызық" ұғымының бейнесін жасаймыз. Сонымен, "сызық" сөзі заттарды
белгілі бір класқа жатқызумен ғана шектеліп^оймай, вдеадды бейнені жасаумен
де байланысты болады. Бізді қоршаған дүниеде үш қой, үш ағаш т.б. ұғымдар
бар, бірақ оңда математикалық сызық ұғымы жоқ. "Сызық" ұғымы заттардың
ортақ қасиеттерін жалпылаумен бірге, ортақ қасиеттерді идеаддап түр.
Идеализациялау абстракциясы бойынша көптеген математикалық ұғымдар куб,
тікбұрышты параллелепипед, шар т.б. пайда болады.
Математикалық ұғымдардың басты ерекшелігі - шыңдық дүние заттарын
тікелей емес, жанама түрде бейнелеуінде.
Математика абстракциялаудың екінші сатысымен де шектеліп қалмайды.
Көптеген математикалық ұғымдар келесі абстракциялау нәтижесінде паңца
болған. Олардың ішінде жазықтықтағы және кеңістіктегі фигуралардың тең
шамалылық ұғымы, одан кейінгі абстракциялау көлем ұғымы болады. Қазіргі
математиканың маңызды ұғымдары болатын топ жөне еріс, векторлық кеңістік
т.б. — көп сатылы абстракциялау нәтижесі.
Көп сатылы абстракциялау нәтижесінде пайда болған математикалық
ұғымдарды өмірде қодцануға болмайды деген жаңсақ пікір тумауы керек.
Кеміңце екі рет абстракциялау кезіңде пайда болатын көлем ұғымы біздің
күнделікті тіршілігімізде кең түрде қодданылады. Ал топ, өріс, көп өлшемді
векторлық кеңістік т.б. ұғымдар ғылым мен техникада қодданыс табуда.
Ұғымның негізгі мінездемелері ретінде:
а) ұғымның мазмұны;
ә) ұғымның көлемі;
б) ұғымның басқа ұғымдармен қатысы және байланысы
қарастырылады.
Ұғымның мазмұны деп ұғымдар класына жататын барлық объектілерге тиісті
елеулі белгілердің жиынтығын айтады. ұғымның көлемі — берілген ұғымдар
класына жататын барлық объектілер жиынтығы. Мысалы үшбұрыш ұғымының мазмұны
"бір түзуде жатпайтын үш нүкте және оларды қос-қостан қосатын үш кесіңді",
яғни үш қабырғасы, үш төбесі және үш бұрышы бар фигура болса, оның көлемі
мүмкін болатын барлық тең қабырғалы, тең бүйірлі, ер қабырғалы үшбұрыштар
бола алады.
Сол сияқты "функция" ұғымының мазмұны — аргументгің әрбір мәніне
белгілі бір ереже немесе заң бойынша функцияның тек қана бір мәні сәйкес
келуі болса, оның көлеміне сызықтық функция, квадраттық функция, көрсеткіш,
логарифмдік функция т.б. жатады.
Сонымен ұғымның мазмұны — оның елеулі белгілері бола-ды да, көлеміне
ұғымға енетін барлық объектілер жиынтығы жатады.
Ұғымның көлемін дұрыс елестету үшін оны "логикалық дөңгелек" арқылы
кескіндеу тиімді. Мүңдағы үлкен дөңгелек берілген ұғымды көрсетсе, оның
ішіндегі кіші дөңгелектер берілген ұғымғажататындарын біддіреді. Мысалы, 9-
суретте үлкен дөңгелек жай бөлшек ұғымы (М) болса, оның ішіңдегі кіші
дөңгелектер жай белшек ұғымына жататын дұрыс (Ң), бұрыс (К) бөлшектер
болады.
Егер ұғымның көлемі көптеген ұғымдарды қамтитын

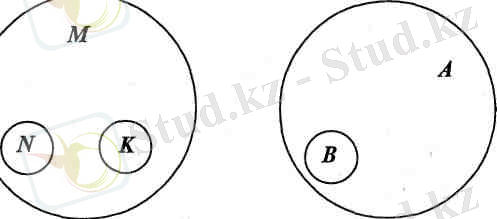
9-сурет 10-сурет
болса, онда берілген ұғымның көлемі кең, ал ол ұғымдар аз болса,
ұғымның көлемі тар делінеді. Егер ұғымның сәйкес класына енетін
объектілердің ортақ, елеулі қасиеттері кеп болатын болса, ұғымның мазмұны
бай, ал оңдай ортақ белгілер аз^эдлса, ұғымның мазмұны кедей деп аталынады.
Ұғымның көлемі мен мазмұны бір-біріне кері қатынаста болады екен,
ұғымның көлемі кең болған сайын, оның мазмұны соғүрлым тарыла береді,
көлемі тарылған сайын, оның мазмұны қорлана түседі.
Егер қандай да бір ұғымның көлемінен белгілі бір ерекшеліктері бойынша
басқа бір ұғымның көлемі бөлініп алынатын болса, оңца алғашқы ұғымның өзі
тегі, ал бөлініп алынған ұғым алғашқыға қатысты оның түрі деп аталынады.
Тектік ұғым мен түрлік ұғымның арақатысы 10-суретте кескінделген. Мысалы,
"үшбұрыш" ұғымдар класынан үшбұрыштың екі қабырғасы тең болатынын бөліп
алатын болсақ, онда "тең бүйірлі үшбұрыш" ұғымы жалпы "үшбұрыш" ұғымының
түрі, (В) ал "тең бүйірлі үшбұрыш" үшін "үшбұрыш" тектік ұғым (А) болады.
Егер тең бүйірлі үшбұрыштардың ішінен бір бұрышы тік болатынын тағы да
бөліп алатын болсақ, ондай жағдайда "тең бүйірлі үшбұрыш" тектік, ал "тең
бүйірлі тікбұрышты үшбұрыш" — түрлік ұғым болып табылады.
Тектік ұғымды түрлік ұғымдардан бөліп алуға мүмкіндік туғызатын белгі
ұғымның турлік айырмашылыгы делінеді. Жоғарыда келтірілген мысалдардағы
үшбұрыштар класынан тең бүйірлі үшбұрыш ұғымын бөліп алатын "екі қабырғасы
тең" белгісі түрлік айырмашылық немесе түрлік ерекшелік болады. Ал тең
бүйірлі үшбұрыштан, тең бүйірлі тікбұрышты үшбұрыш ұғымын бөліп тұратын
"бір бұрышы тік" белгісі түрлік ерекшелік болады.
Тектік ұғымнан түрлік ұғымға ету ұғымды шектеу (ұғымның келемін
кеңейту) деп аталады.
Егер ұғымдар бір-бірімен тектік және түрлік қатынаста болса, олар өзара
багынышты делінеді. Түрлік ұғымдар тектік ұғымға бағынышты болады. Мысалы,
"үшбұрыштар" ұғымына "тең бүйірлі", "тең қабырғалы", "өр түрлі қабырғалы
үшбұрыштар" немесе "сүйір бұрышты үшбұрыш", "доғал бұрышты үшбұрыш",
"тікбұрышты үшбұрыш" ұғымдары бағынышты.
түрлік ұғымдарға қойылады. Мысалы, "жай сандар" мен "құрама сандар",
"рационал саңдар" мен "иррационал сандар", "тіктөртбұрыш" пен "ромб",
"квадраттендеу" мен "сызықтық теңдеу" салыстырылады.
Мектептегі оқыту процесінде тектік ұғымдарды түрлік ұғымдармен
шатастыру да жиі кездеседі. Мәселен, есептің шартында кез келген тертбұрыш
туралы әңгіме болғанда оқушылар кез келген төртбұрыш сызудың орнына
тіктертбұрышты немесе квадратты кескіндейді. Нәтижесіңце, есептің шартына
енбейтін тіктәртбұрыштың немесе квадраттың қасиеттерін еріксіз қолдануға
тура келеді де, есепті шығаруға кедергі жасайды, не оны қате шығарады.
Немесе есептің шарты бойынша кез келген үшбұрыш болатын болса, оның орньша
тең қабырғалы үшбүрьші, не тікбұрышты үшбұрыш сызып қателесетіңдер де жиі
кездеседі.
Мұндай жағдайлар оқушылардың қоршаған ортадан тіктөртбұрышты жалпы
тертбұрыш кескінінен көбірек кездестіруіне байланысты болса, екінші жағынан
оқыту про-цссінде тортбұрыш тақырыбын өтуге байланысты "төртбұрыш"
ұғымы мен оның дербес түрі болатын "тіктөртбұрыш" ұғымы арасындағы
қатынастар жігін ажыратуға жете назар аудармаудан болатын жағдай. Сондықтан
да оқушы "төртбұрыш" терминін "тіктөртбұрышпен" шатастырады.
Ұғымдар арасындағы бағыныштылық қатынастар қарапайым болғанымен, бұл
мөселеге ете үқыптылықпен қарауға тура келеді.. Мүғалім ұғымдар арасыңцағы
өзара бағыньшпылық қатынасты оқушыларға көптеген қарапайым және нақтылы
мысалдар арқылы түсіндіріп отыруы керек. Мүнда анықтама, түжырымдау, оның
құрылысымен таныстыру, ұғымдарды жіктеу жүмыстарының маңызы зор.
Математикалық ұғымдарды қалыптастыру
Қандай да болмасын білімге талпыну, танымдық ізденімпаздықты арттыру,
соның ішінде математикалық білімді игеріп, іскерлік пен дағдыны
қалыптастыру — маңызды да қиын меселе. Танымдық іс-әрекеттер арнайы
құрылған проблемалық ахуаддар кезінде пайда болады да, оны оқушылар бұрын
немесе жаңадан игерген нақты жүмыстарда жөне басқа пәндерді оқып-үйренуде
үнемі өз қажетіне жарата алады.
Жалпы алғанда математиканы оқып-үйрену ұғымды қалыптастыру мен оны
терең танымдық дәрежеге жеткізуден, математикалық түжырымдарды,
теоремаларды дәлелдей білуге үйретуден және оны нақтылы іс-әрекетте, есеп
шығаруға қолдана білуден тұрады. Мұның алғашқысы да, маңыздысы да
математикалық ұғымдарды игеру болғандықтан, оның алатын орны да ерекше.
Оқушының білім-танымының бастауы, оның қолданылар аясының кеңдігі мен
түсінілуі үшін мүғалімнің өзі олармен жете таныс әрі оның қасиетінен жан-
жақты хабардар болуы керек. Сонда ғана шындық дүниенің заттары мен
құбылыстары туралы оқушы дұрыс түсініктер алып, олар туралы тура ой түзеді.
Мұның өзі баланың дамуына, ойының жетілуіне игі әсер етіп, алған таным-
білімдерін әрі қарай толықтырып, үштап, күнделікті өмщде қолдана білуіне
жол ашады.
Ұғымдарды меңгермейінше заңдар мен теорияларды саналы түрде білу
мүмкін емес, өйткені олардың өзі ұғымдар арасындағы байланыстарды
білдіреді. Ал ұғымды меңгеру дегеніміз — болмыстың, заттар мен
құбылыстардың маңызды қасиеттерін, олардың арасындағы мәнді байланыстарды,
арақатынастарды білу.
Ғылыми зерттеулер мен адамның практикалық қьізметінде кеңінен
қодданылып жүрген, ғылымның "қаруы" ретінде қабыдданған ұғымдардың мазмұны
оқу процесінде біртіндеп ашылады. Ұғымды меңгеру оқушылардың белсенді ой
қызметімен, анализ және синтез, салыстыру, абстракциялау және жалпылау
сияқты ойлау амалдарын (операцияларды) орындаумен байланысты. Сондықтан
ұғымдарды қалыптастыру оқушылардың ойлауын дамытумен тікелей байланысты.
Ұғым туралы психолог В.В. Давыдов "Балаларға жалпылау мен ұғымды
қалыптастыру мектептің басты міндеттерінің бірі болып табылады" [22,53-
бет],— деген.
Математикалық ұғымдар жалпылау мен абстракциялаудьщ жоғары деңгейі
болғаңдықтан мектеп курсында оған ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.