Математикалық статистика: таңдамалық үлестірім, полигон-гистограмма, жинақтылық, орталар және сызықты корреляция


Е. Д. Тлеукеев
Математикалық статистика
Түркістан -2012
№1 Типтік жұмыс.
Тақырыбы: Таңдама үлестірімі. Полигон және гистограмма.
1) Таңдама үлестірімі.
Статистикада қарастырылып отырған объектілер жиынын бас жиын деп атаймыз. Бас жиыннан кездейсоқ алынған жиынды таңдама деп атайды. Таңдамадағы объектінің санын таңдаманың көлемі деп аталады. Таңдамадағы мәліметтердің әр түрлерін х 1 , х 2 , х 3, . . . , х n деп белгілейді де оларды варнациаттар деп атайды. Егер варнациаларды өсу ретімен орналастырсақ варнациялық қатар аламыз.
х 1 , х 2 , х 3, . . . , х n
n 1 , n 2 , . . . , n n сандары варнациалық қатардың жиіліктері деп аталады және олардың қосындысы таңдманың көлеміне тең;
n 1 + n 2, + . . . + n n n
Ал, жиіліктердің таңдама көлеміне қатысты
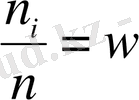 варнациалық қатардың салыстырмалы жиілігі деп аталады және олардың қатынасы бірге тең.
варнациалық қатардың салыстырмалы жиілігі деп аталады және олардың қатынасы бірге тең.
w 1 + w 2 + . . . + w n
Таңдаманың варнациалық қатарымен бірге жиіліктері немес салыстырмалы жиіліктері көрсетілсе, таңдама үлестірмелі берілген деп аталады.
2) Полигон және гистограмма .
Тік бұрышты декарттық координаалар жүйесінде (x 1 , n 1 ), (x 2 , n 2 ), . . . , (x n , n k ) нүктесіне салып, оларды кесінділермен тізбектей қоссақ, сонда пайда болған санақ сызықтар тізбегін жиілік полигоны деп аталады.
Әрбір кіші интервалдағы таңдама жиілігінің интервал ұзындығына қатынасын
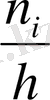 жиілік тығыздығы деп аталады. Табаны - h, биіктігі -
жиілік тығыздығы деп аталады. Табаны - h, биіктігі -
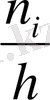 болатын тік төртбұрыштардан тұратын фигураны жиілік гистограммасы деп аталады.
болатын тік төртбұрыштардан тұратын фигураны жиілік гистограммасы деп аталады.
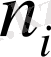
4
3
2
1
2. 1 3 4. 2 5 5. 3 6 6. 1 6. 5 7. 2 8 x i
Дербес орталық
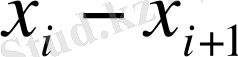
x i -x i+1
1
2
3
4
5
6
7
8
9
10
[2, 1 - 2, 69]
(2, 69 - 3, 28]
(3, 28 - 3, 87]
(3, 87 - 4, 46]
(4, 46 - 5, 05]
(5, 05 - 5, 64]
(5, 64 - 6, 23]
(6, 23 - 6, 82]
(6, 82 - 7, 41]
(7, 41 - 8, 00]
3
2
0
4
3
2
4
2
4
5
5, 1
3, 3
0
6, 7
5, 1
3, 3
6, 7
3, 3
6, 7
8, 4
n i /h n=29
8. 4
6. 7
5. 1
3. 3
1. 7
2. 1 2. 69 3. 28 3. 87 4. 46 5. 05 5. 64 6. 23 6. 82 7. 41 8 x i -x i +1
№2 Типтік жұмыс.
Тақырыбы: Таңдамалы жинақтылығының санақнамалық үлестірімділігі берілген.
Шешуі:
а) Анықтаманы пайдаланып таңдамалы орта мен дисперсияны есептейік:
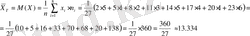
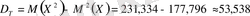
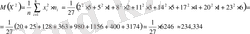
б) Көбейту әдісімен таңдамалы орта және дисперсияны есептейік. Ол үшін кесте құрамыз:
 u
i
u
i
 u
i
2
u
i
2
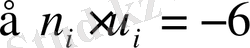
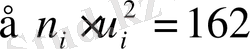
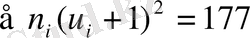
Бірінші тік жолға варианталарды жазамыз. Екінші тік жолға жиіліктерді жазамыз; жиіліктердің қосындысын(n=27) тік жолдың төменгі торына орналастырамыз.
Тік жолдың орта шенінде орналсқан вариантты жалған нөл ретіндеалып, үшінші тік жолда жатқан сол торға 0-ді жазамыз, сол нөл жазылған тор көзден жоғары қарай -1, -2, -3, -4 сандарын жазамыз.
n i жиіліктердің u i шарттарын варианталарға көбейтіп төртінші тікжолға жазамыз.
Жиіліктерді сәйкес келетін шартты варианталар , яғни
.
Жиіліктерді сәйкес келетін шартты варианталарын бірге арттырғандағы квадратына көбейтеміз. Сандар қосындысын (177) алтыншы тік жолдың төменгі торына жазамыз. Есептеуді тексеру үшін мына теңдікті пайдаланамыз:
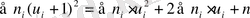
Тексеру:
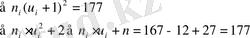
177=177. Шарт орындалды.
Бірінші және екінші ретті шартты қарымдарын есептейміз.
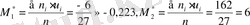
Қадамды табамыз: h=8-5=3
Жалған нөл c=14-ті ескере отырып, іздеп отырған таңдамалы орта және дисперсияны есептейік.
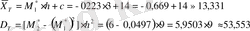
в) Қосынды әдісімен таңдамалы орта және дисперсияны есептейік. Ол үшін кесте құрамыз.
1. Бірінші тік жолға варианталарды жазамыз.
2. Жиіліктерді екінші тік жолға жазамыз, жиіліктердің қосындысын (27) тік жолдың төменгі торына орналастырамыз.
3. Үшінші тік жолдың орта шенінде алынған торға жалған нөл жазып, сол жатық жолдың келесі тік жолымен қиылысқан нөлмен белгілеп, оның үстіне және астына, көршілес торларына бір-бір нөлден жазамыз.
4. Үшінші тік жолдың нөлдің үстіне толтырылмай қалған торларына тізбектеп жиналған жиіліктердің жиналуын b 1 =30 үшінші тік жолдың жоғарғы торына орналастырамыз. Үшінші тік жолдағы нөлден толтырылмаған торларына тізбектеп жинақталған жиіліктерді қосып a 1 =24, ең төменгі торына жазамыз.
5. Дәл осыендай жолмен төртінші тік жолды толтырамыз, бірақ үшінші тік жолдағы жиіліктер қосылады. Нөлдің үстіндегі орналасқан жинақталған жиіліктерді қосып b 2 =35 төртінші тік жолдың ең жоғарғы торына орналасытрамыз.
Нөлдің астындағы орналасқан жинақталған жиіліктердің қосындысын a 2 =19 төртінші тік жолдың төменгі торына орналастырамыз.
Енді d 1 , s 1 , s 2 , -ні табайық.
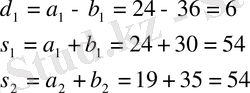
Бірінші ретті және екінші ретті шартты қарымдарды іздейік:
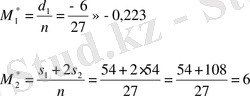
Қадамды h=3 және жалған нөл c=14 ескере отырып ізделінген таңдамалы орта мен дисперсияны есептейік:
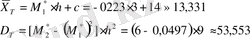
№3 Типтік жұмыс.
Тақырыбы:Жай орталар(Простые средние)
Aрифметикалық орта (Арифметическое среднее)
а) Жай вариациялық қатар үшін арифметикалық ортаны есептеу :
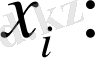 2, 3, 5, 6, 8, 9, 10, 14, 15, 17, 18, 20, 22, 24, 27, 28, 29, 31, 32, 34
2, 3, 5, 6, 8, 9, 10, 14, 15, 17, 18, 20, 22, 24, 27, 28, 29, 31, 32, 34
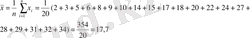
б) Топтастырылған вариациялық қатар үшін арифметикалық ортаны есептеу :
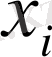
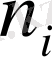
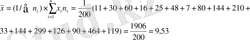
в) Интервалдық топтастырылған вариациялық қатар үшін арифметикалық ортаны есептеу :
[1-3]
(3-5]
(5-7]
(7-9]
(9-11]
(11-13]
(13-15]
(15-17]
(17-19]
(19-21]
(21-23]
(23-25]
(25-27]
(27-29]
(29-31]
(31-33]
(33-35]
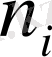
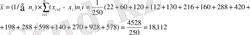
Гармоникалық орта (Гармоническое среднее )
а) Жай вариациялық қатар үшін гармоникалық ортаны есептеу :
2, 3, 5, 6, 8, 9, 10, 14, 15, 17, 18, 20, 22, 24, 27, 28, 29, 31, 32, 34

б) Топтастырылған вариациялық қатар үшін гармоникалық ортаны есептеу :

в) Интервалдық топтастырылған вариациялық қатар үшін гармоникалық ортаны есептеу :

Геомертиялық орта (Геометрическое среднее. )
а) Жай вариациялық қатар үшін геометриялық ортаны есептеу :
 б) Топтастырылған вариациялық қатар үшін геометриялық ортаны есептеу :
б) Топтастырылған вариациялық қатар үшін геометриялық ортаны есептеу :
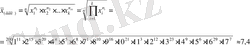
в) Интервалдық топтастырылған вариациялық қатар үшін геометриялық ортаны есептеу :

№4 Типтік жұмыс.
Тақырыбы:Құрылымдық орталар (Структурные средние)
Медиана
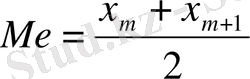
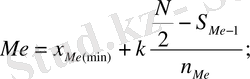
а) Жай вариациялық қатар үшін медиананы есептеу :
2, 3, 5, 6, 8, 9, 10, 14, 15, 17, 18 , 20, 22, 24, 28, 29, 31, 32, 34
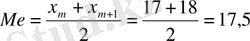
б) Топтастырылған вариациялық қатар үшін медиананы есептеу :
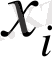
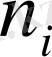
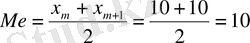
... жалғасыв) Интервалдық топтастырылған вариациялық қатар үшін медиананы есептеу :
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz