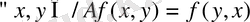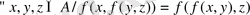Математиканың бастауыш курсының негіздері: бастауыш сынып мұғалімдерін даярлауға арналған оқу-әдістемелік құрал


Б. ДАУЛЕТБЕКОВА, Ж. ШАЛАБАЕВА

Б. ДАУЛЕТБЕКОВА, Ж. ШАЛАБАЕВА
БАСТАУЫШ СЫНЫП МҰҒАЛІМДЕРІН ДАЯРЛАЙТЫН ЖОҒАРЫ ЖӘНЕ АРНАУЛЫ ОҚУ ОРЫНДАРЫ СТУДЕНТТЕРІНЕ АРНАЛҒАН
ШЫМКЕНТ, 2010 Ж.
ББК 22. 11 я 73
Д 45
Пікір жазғандар:
Ү. Рахмет - педагогика ғылымдарының кандидаты, профессор.
С. Тазабеков - физика-математика ғылымдарының кандидаты, доцент.
Оқу құралын баспаға Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университетінің оқу-әдістемелік кеңесі мақұлдаған (№5 хаттама, 26-ақпан 2010 ж. )
Д 45 Б. Даулетбекова, Ж. Шалабаева
МАТЕМАТИКАНЫҢ БАСТАУЫШ КУРС НЕГІЗДЕРІ
Б. Даулетбекова, Ж. Шалабаева - Шымкент, 2010. - 152 бет.
ISBN 9965-14-616-5
Оқу құралын жазу барысында Қазақстан Республикасы жалпы орта білім берудің мемлекеттік жалпыға міндетті стандарты (бастауыш білім), типтік оқу бағдарламасы, оқулықтарға арналған әдістемелік нұсқаулар және жаттығулар қолданылды.
Оқу құралы бастауыш сыныптарда қарастырылатын математикалық ұғымдарды оқыту жүйесін меңгеруге мүмкіндік туғызады.
Бұл құралда математикадан бақылау жұмысын орындау туралы жалпы нұсқаулар, тақырыптары мен тапсырмаларды орындау үлгілері көрсетілген.
Оқу құралы бастауыш сынып мұғалімдерін даярлайтын жоғары оқу орындары мен колледж студенттеріне арналған
Д
ISBN 9965-14-616-5
2010
© Б. Даулетбекова, Ж. Шалабаева
К І Р І С П Е
Жалпы білім беретін мектептің оқу бағдарламасында: «Бастауыш сатыда білім берудің түбегейлі мақсат, міндеттерін жүзеге асыруда әр оқу пәнінің өз орны мен рөлі бар. Математика ақиқаттың ең маңызды саласы және адамның алуан түрлі коммуникативтік жағдайларға еркін араласып қатысу, сауатты бағдарлай алу қабілетін дамытып, жүзеге асыратын табиғи және жасанды тілдер туралы оқушының қажетті білім алуына, ауызекі сөйлеуін дамытуға, ойын сауатты жеткізе білу біліктерін қалыптастыруға, дүниені математикалық өрнектер арқылы бейнелеп қабылдауға кеңінен жол ашатын, танымдық, тәрбиелік, дамытушылық мүмкіндіктері мол жетекші пән ретінде қарастырылады», - деп атап көрсетілген.
Осындай күрделі мәселенің дұрыс шешілуі ұстаздардың теориялық білімінің және кәсіби мамандығының деңгейіне байланысты.
Болашақ бастауыш мектеп мұғалімінің кәсіби даярлығы әр түрлі оқу, арнайы және факультативтік пәндерді оқып-үйрену барысында жүзеге асырылатын психологиялық-педагогикалық, пәндік теориялық және дербес әдістемелік дайындықты қамтиды. Бұлардың ішінде математикалық ұғымдар, заңдар, қасиеттер, фактілер, әрекет тәсілдері, логикалық амалдар мен ақыл-ой операцияларын қарастыратын математиканың бастауыш курсы негіздері пәні ерекше рөл атқарады.
Математика курсы бастауыш сынып мұғалімі бөлімі студенттеріне аса күрделі, маңызды математикалық ұғымдар мен фактілердің мән-мағынасын ашып көрсету, бастауыш сынып оқушыларына математиканы табысты оқытып-үйрету, оларды осы оқу пәні арқылы тәрбиелеу мен дамытуда қажет болатын теориялық әзірліктің іргетасын қалау мақсатын көздейді.
Курс мазмұны және оның құрамына кіретін мәселелерді қарастырудың реті мұғалімдердің математикалық білімін тереңдете әрі кеңейте түсуге қатысты өзіндік жұмыс тұрғысынан, сондай-ақ орта буын математикасы талаптары тұрғысынан алғанда бастауыш мектеп мұғалімдерінің шығармашылық мүмкіндігін арттыра түседі.
Математиканың бастауыш курсының өзекті мәселесі - теріс емес бүтін сандар, олармен жүргізілетін амалдар және олардың қасиеттері мен заңдары болып табылады. Әр алуан қырынан (реттік, еселік, шаманың шешуші, есептеу барысының нәтижесі) қарастырылып, натурал сан мен нөл ұғымдарын, сондай-ақ есептеулер жүргізу біліктері мен дағдыларын қалыптастырудың теориялық негіздері болып табылады.
«Алгебра мен геометрия элементтері», сондай-ақ «Сан ұғымының кеңеюі» тақырыбының табиғи жалғасы мен қорытындысы ретінде «Шамалар және оларды өлшеу» мәселелері сан ұғымымен тығыз байланыста қарастырылады. Мектеп математикасы курсында сан мен шама ұғымдары математиканың «жиын», «сәйкестік», «қатынас» және т. с. с. жалпы ұғымдарына сүйеніп енгізіледі. Шын мәнінде, бұл жалпы ұғымдар мектеп математикасы курсында айқын емес түрде қолданылады.
Сондықтан болашақ бастауыш мектеп мұғалімдері белгілі бір жалпы математикалық ұғымдар жүйесімен таныс болуы тиіс. Осыған орай математика курсы жиындар және оларға қолданылатын амалдар, сәйкестіктер, комбинаторика, есеп және оны шешу үдерісі, алгоритмдер сияқты жалпы ұғымдарды оқып-үйренуден басталуы кездейсоқтық емес. Мұнда жиындар теориясы мен математикалық логика элементтері мектеп математикасы курсының негізін құрайтындықтан және оны тиісті математикалық тілмен қамтамасыз ететіндіктен барынша тереңірек баяндалады. Бұл жалпы ұғымдар, сондай-ақ әр алуан жиындар туралы білімдер «Алгебра элементтері» тақырыбында, атап айтқанда «өрнек», «теңдеу», «теңсіздік», «тендеулер жүйесі», «теңсіздіктер жүйесі мен жиынтығы» және т. б ұғымдарды қарастыру барысында кеңінен қолданылады.
Оқушының оқуға деген қызығушылығын оятудың маңызды құралдарының бірі математиканы өмірмен байланыстырып оқытуды қамтамасыз ету. Теориялық материалды оқытқанда мазмұны қоршаған дүниенің өмір жағдайларымен байланысты күнделікті өмірде жүзеге асыруға болады.
Оқу құралында педагогикалық жоғары оқу орындарында болашақ бастауыш мектеп мұғалімдерінің кәсіби даярлықтарын жақсартудың маңызды алғы шарттарының бірі -өзбетінше бақылау жұмыстарын орындау болып табылады.
Оқу құралында бастауыш мектептің математика курсында қарастырылатын алгебралық және геометриялық ұғымдардың түсініктемелері қысқаша лекция түрінде жазылып, әр тақырыпқа байланысты бақылау сұрақтары мен жаттығулар, соңынан бақылау жұмысын орындау туралы жалпы нұсқау және тапсырмаларды орындау үлгілері мен бақылау жұмыстарының тапсырмалары келтірілген.
«МАТЕМАТИКАНЫҢ БАСТАУЫШ КУРСЫНЫҢ НЕГІЗДЕРІ» пәнінен берілетін білім мазмұны
Қазақстан Республикасының «Білім туралы» заңында «Білім беру жүйесінің басты міндеті - ұлттық және жалпы азаматтық құндылықтар, ғылым мен практика жетістіктері негізінде жеке адамды қалыптастыруға және кәсіби шыңдауға бағытталған білім алу үшін қажетті жағдайлар жасау, оқытудың жаңа технологияларын енгізу, білім беруді ақпараттандыру, халықаралық ғаламдық коммуникациялық желілерге шығу» деп, білім беру жүйесін одан әрі дамыту міндеттері көзделеді.
Білім алуға, шеберлікке, іс-әрекет дағдыларына үйрету мен меңгеру барысы және адамды өмір мен еңбекке бейімді етіп даярлаудың негізгі құралы - оқыту. Оқыту барысының нәтижесінде білім беру мен тәрбие мақсаттары жүзеге асырылады. Түрлі оқу орындарындағы оқыту - білім берудің басты жолы, сол сияқты оқу отбасында, өндірісте, жұмыста т. б. күнделікті адамның тіршілік және қызмет барысындағы жағдайларды іске асып отырады.
Оқытудың мазмұны мен сипаты қоғамның материалдық және мәдени даму дәрежесіне сай белгіленеді. Оқудың мақсаты мен мазмұны, оны ұйымдастырудың түрлері мен әдістері адамзат қоғамының даму кезеңдеріндегі қоғамдық қатынастар негізінде жалпы білімге, адамдардың даярлығы негізінде қойылатын талаптардың сипатына және оқыту жөніндегі педагогикалық идеяларға сай өзгеріп отырады.
Білім беру саласындағы болып жатқан өзгерістер соңғы жылдары педагогикалық білім алатын болашақ мамандарға, олардың кәсіби дайындықтарына елеулі талаптар қоюда. Әсіресе, бастауыш сынып мұғалімдерін даярлауға қойылатын талаптар күрделі де сан-салалы болып отыр.
Себебі, бастауыш сынып мұғалімі - жас ұрпақ бойына ең алғашқы білім негіздерін сіңіретін, олардың дағдылары мен машықтарын дұрыс бағытта қалыптасуын қамтамасыз ететін, ізгілікті және отаншылдық қасиеттерге баулитын тұлға.
Мемлекеттік білім стандартында бастауыш сынып мұғалімдеріне кәсіби жан-жақты теориялық және практикалық білім мен дағдыларды, әлеуметтік және гуманитарлық пәндер негіздері өнерпаздық қабілеттерді, оқыту мен ақпараттық технологияларды пайдалану дағдыларын, іскерлік машықтарын жан-жақты меңгерту көзделген.
«Математиканың бастауыш курсының негіздері» пәні болашақ мұғалімдерге математиканы табысты оқытып-үйретуге, оқушыларды бастауыш математика курсы ұғымдарының негізгі мектепте қолданылу мүмкіндіктерін көре білуге қажет болатын даярлықты қамтамасыз етеді.
«Математиканың бастауыш курсының негіздері» пәні болашақ бастауыш сыныптар мұғалімдерінің кәсіби даярлығы жүйесіндегі арнаулы пән ретінде өткен ғысырдың жиырмасыншы жылдары жоғары мектеп жұмысын ұйымдастырудың бірыңғай мемлекеттік принциптері анықталған кезде қалыптаса бастады.
Бастауыш сынып мұғалімдеріне кәсіби теориялық білім педагогика, психология, әдістеме ғылымдарын оқытумен бірге бастауыш сыныптардағы негізгі пәндер - қазақ (орыс) тілі, математика, ана тілі, бейнелеу өнері, дүниетану, музыка т. б. ғылымдардың негіздерін меңгерту арқылы да белгілі.
Осы тұрғыда бастауыш сыныпта берілетін математикалық білім мазмұны мен оқушылардың даярлықтарының міндетті деңгейіне қойылатын талаптар басты назарға алынады. Мектептің бастауыш сатысында берілетін математикалық білім мазмұны қарапайым математикалық түсініктерді қалыптастыру, сандар нумерациясы, алгебра және геометрия элементтері, шамалар және оның өлшем бірліктері деп аталатын бөлімдерден тұрады.
Әрбір мұғалім математика пәнінде оқушыларды терең ойлай білуге, олардың шығармашылық қабілеттерін дамытып, өз бетінше жұмыс жасай білуге үйрету мақсатын қояды.
Бұл мақсатты орындау, яғни оқушылардың білім, білік, дағдысын, өзіндік танымын қалыптастыру - нақты ұйымдастырылған кезеңдер арқылы жүзеге асырылатын күрделі үрдіс.
Жалпыға міндетті орта білім стандарттарында (жалпы бастауыш білім) білім объектісі ретінде - білім мазмұны алынған болса, өркениетті елдердің тәжірибесінде білім нысаны ретінде - оқыту нәтижесі алынған. Осыған орай білім мазмұнын жаңарту мен оқытудың инновациялық әдістерін өндіру бүгінгі күннің талабы болып отыр.
Білім сапасы оның төрт сипатын (білім - құндылық, білім - жүйе, білім - үдеріс, білім - нәтиже) біртұтас қарастыра отырып, олардың ішінде білімнің құндылық ретіндегі және білімнің нәтиже ретіндегі сипатына мән берумен тікелей байланысты.
«Математика» білім саласы бойынша күтілетін нәтижелер білім мазмұнының жетекші компоненттері және білім, түсіну, қолдану, жоғарғы сипаттағы біліктер деп аталатын категориялар арқылы бейнелеген оқу материалдарын меңгеру деңгейлерін ескере отырып анықталады.
Мұнда басты есте болатын нәрсе - оқушылардың математикалық мәдениетін көтеру, математиканы оқып-үйренуге ынталандыру, нақты дағдыларды бекіту.
«Бастауыш оқытудың педагогикасы мен әдістемесі» мамандығы бойынша оқылатын «Математиканың бастауыш курсының негіздері» пәнінің білім мазмұнын қысқаша кесте түрінде көрсетсек:
Қазіргі кезде білім беру саласында болып жатқан ауқымды өзгерістер түрлі ынталы бастамалар мен түрлендірулерге кеңінен жол ашуда. Осы қарастырылған мәселелер реті болашақ бастауыш сынып мұғалімдерінің оқушылардың математикалық білімін тереңдете және кеңейте түсуімен қатар шығармашылық ізденісін қамтамасыз етеді.
Бастауыш мектеп жасындағы оқушыларға математиканы оқытудың әдістемелік жүйесінің өзіндік ерекшеліктерін сипаттайтын әдістемелік ережелер, сондай-ақ оқытуға тұлғалық-іскерлік пен дамытушылық тұрғыдан қарау әдістемелік құрал мазмұнын құрайды.
1. МАТЕМАТИКАЛЫҚ ҚҰРЫЛЫМДАР
Құрылымдардың типтері және олардың сипаттамалары
Мақсаты:
1. Математикалық құрылымдарына жалпы ақпарат.
2. Математикалық құрылымдардың типтері мен олардың сипаттамаларына
түсініктеме.
Математика басқа ғылымдар сияқты бізді қоршаған әлемді зерттейді және де ол зерттейтін нақты әлемнің құбылыстары өздерінің материалдық табиғатымен емес, тек қана формальды құрылымдық қасиеттерімен, әсіресе олармен байланысты сандық қатынастар мен кеңістіктік формаларымен анықталады.
Қазіргі математика таза теориямен, сонымен бірге оның қолданбалы салаларымен айналысатын ғалым-математиктердің күш-жігері арқасында қарқынды даму кезеңін бастан кешіруде. Олардың кейбіреулері үшін математика - қоршаған ортаны және онда болып жатқан құбылыстарды тану әдісі болса, басқалар үшін математиканың өзі зерттеуге және дамытуға лайықты біртұтас әлем болып табылады.
Сонымен бірге, математиканың дамуы көптеген шиеленіскен қарама-қайшылықтардың, нақты мен абстрактының, дара мен жалпының, форма мен мазмұнның, аксиоматика мен конструктивтіктің, шекті мен шексіздің, формальдық пен мазмұндылықтың, дискреттік пен үздіксіздіктің күрес үдерісінде жүзеге асады. Мысалы, соңғы он жылдықтарға тән болып отырған дәл ғылым салаларының қарқынды дамуы математиканың одан әрі кеңейе түсуіне және мамандыққа бейімделуіне кең жол ашты, тұтас ғылым математиканың ішінде әртүрлі зерттеу пәні мен әдістері, ерекше белгілеуі бар дербес дамитын бөлімдер пайда бола бастады.
Математика зерттейтін ән, ол өзінің даму барысында ылғи өзгеріске ұшырап, кеңейіп отырады. Егер ХІХ ғасырдағы және ХХ ғасырдың бірінші жартысындағы математика сандар мен шамалар жайындағы ғылым болса, онда қазіргі математика қазіргі математика, Н. Бурбаки айтқандай, математикалық құрылымдардың заңын зерттейді. Математикалық танымның дамуында жаңа нысандар ылғи ашылады, ал жаңа нысандар жаңа сандық қатынастарды тану құралы, ендеше, оның зерттеу пәні кеңейе береді.
Николай Бурбаки - Францияның белгілі атақты математиктер тобын біріктіретін топтың жалған немесе лақап аты. Бұл топтың құрамы, жас ерекшеліктері және басқа да қасиеттері белгісіз жасырын ұйым. Кейбір зерттеушілердің пікірінше, оның құрамына Картан, Папи, Кофман, Фор, Мандельброт т. б. енді деп болжайды. Бұл жөніндегі кейбір мәліметтерді американ математигі П. Р. Халмоштың «Николай Бурбаки» деген мақаласынан табуға болады.
Н. Бурбакидің негізгі мақсаты математика бойынша «Математика элементтері» атты толық трактат жазу. Тракттағы алғашқы абстракция немесе жалпы принцип ретінде математикалық құрылым және оны зерттеуге сәйкес әдіс ретінде аксиоматикалық әдіс қарастырылады.
Н. Бурбаки «Математика элементтері» атты бірнеше томдарын жарыққа шығарды және олар өзінің жоғары ғылыми-теориялық дәрежесі мен материалды баяндаудың стилі жағынан дүниежүзі математиктерінің құрметіне бөленді
Н. Бурбакидің пікірінше, математика ғылымы математикалық құрылымдарды зерттейді.
Сонымен, математиканың бірден-бір нысаны математикалық құрылымдар болып табылады.
Математикалық құрылымдар базистік және көп еселі болып екіге бөлінеді. Алгебралық, топологиялық және реттік құрылымдар базистік деп аталады. Бүкіл математика ғылымы осы үш түрлі базистік құрылымдардың жиынтығы мен комбинациясы.
Мысалға, группа, сақина және өріс - алгебралық құрылымның түрлері.
Нақты сандар жиыны мен натурал сандар жиыны - реттік құрылымның түрлері, ал топологиялық кеңістік пен топологиялық векторлық кеңістік- топологиялық құрылымның түрлері.
Математикалық құрылым деп мынадай жиынды айтамыз:
- табиғаты кез келген элементтер жиыны (сан, функция, вектор, тензор, матрицалар т. б. ) ;
2) элементтер арасындағы берілген қатынастар;
3) осы қатынастар үшін анықталған белгілі бір амалдар (композициялар немесе амалдар) ;
4) операциялардың негізгі қасиеттері аксиомалар жүйесі арқылы түсіндіріледі. Мысалы, алгебралық құрылымды қарастыралық. Группа теориясында үшінші элемент қалған екі элементтің функциясы немесе үшінші элемент қалған екі элементтің арасындағы қатынас бойынша анықталады. Қатынастың осындай түрі сақина мен өріске де тән. Мұндай қатынасты «композиция заңы», ал амалдың өзін «алгедралық амал» деп атайды. Осындай жиын алгебралық құрылым делінеді. Группа теориясының аксиомалар жүйесі «алгебралық амалдардың» негізгі қасиеттерін түсіндіреді. Берілген құрылымның теориясын құру қабылданған аксиомалар жүйесінен қажетті логикалық нәтижелерді, теоремаларды алу. Өзінің аксиоматикалық формасында математика абстрактілік формалардың - математикалық құрылымдардың жиынтығы. Математикалық құрылым ұғымы жиын мен функция ұғымдарын жалпылаудың, яғни абстракцияларды абстракциялаудың нәтижесінде пайда болған деген.
Алгебралық пен топологиялық және реттік құрылымдары базистік делінеді, өйткені математикалық теорияларды құру солардан басталады. Осындай базистік құрылымдардың өзара әсерінен немесе қосылысынан көп еселі делінетін күрделі математикалық құрылымдар пайда болады. Әдетте, мұндай құрылымдар ең кемінде екі базистік құрылымдардың комбинациясы болып табылады.
Мысалы, нақты сандар жиынында үш базистік құрылым комбинациясы бар, ендеше бұл жиын үш еселі құрылым делінеді.
Математика - математикалық құрылымдар жайындағы ғылым. Мұндай түсініктің үлкен әдістемелік және педагогикалық маңызы бар. Біріншіден, математика ғылымының негізінде құрылым ұғымы жатыр, бүкіл математика ғылымы математикалық құрылымдарды зерттейді, ендеше құрылымдық бірлік математикалық білімнің синтезін, математикалық ғылымдардың ішкі бір тұтастығын тамаша дәлелдейді. Екіншіден, математикалық білімді синтездеуде математикалық құрылым ұғымымен бірге аксиоматикалық әдіс үлкен роль атқарады. Аксиоматикалық әдіс математикалық ойды әжептәуір үнемдеуде және математикалық құрылымдарды зерттеуде құнды әдіс болып табылады.
Математиканың арнаулы бөлімдері қандай-да арнаулы құрылымдар тегіне тиісті құрылымдармен айналысады. Әрбір құрылымдар тегі сәйкес аксиомалар жүйесімен анықталады, яғни математика - математикалық құрылымдар жайындағы ғылым.
Н. Бурбаки еңбектерінде ғылыми дәлдіктің қазіргі деңгейінде құрылған және тым жалпы принциптерге сүйенген барлық математикаға шолу жасалынған.
Н. Бурбаки зерттеулерінде ядросы жиындар болатын бір ғана математиканың бар екендігі, ал математиканың әртүрлі тармақтарында түрліше көрініс беруі және сәйкес теорияның барлық құндылығы осы теорияны зерттейтін құрылымның қандайда бір типімен айқындалған жиын элементтінің байланысына тәуелділігі көрсетілген.
«Математикалық құрылым» ұғымын қалыптастыру әлемді танудың маңызды ғылыми құралы - аксиоматикалық әдістің дамуымен байланысты. Мысалы, қазіргі кезде осы күнгі математиканың көптеген бағыттары тек қана аксиоматикалық әдістің яғни, сәйкес аксиомалар жүйесінің негізінде құрылады. Ал математика ғылымының әр саласына тән аксиомалардың өзі ұзақ және күрделі тарихи даму үдерісінде пайда болды.
«Құрылым» ұғымының басты ерекшелігі табиғаты әр алуан болатын жиын элементтеріне оның жарамды болатындығында және де қарастырылатын қатынастар сипатының таңдалу тұрғысынан жоғары дәрежеге ие екендігінде.
Математикалық құрылым - жаңа математикалық ұғым, сандық қатынастар мен кеңістік формаларды толығырақ, кеңірек және тереңірек бейнелейтін абстракция. Философиядағы сан категориясы -ең жалпыланған түсінік және бүкіл таным тарихының нәтижесі, ойлау формасы. Ондағы материя категориясын физикадағы зат немесе өріске теңестіруге ешбір болмайтыны сияқты, сан категриясында математикадағы санға, шамаға немесе математикалық құрылымға ешбір теңестіруге болмайды. Сан, шама және математикалық құрылым - сан категориясының түрлері. Келешекте санның жаңа түрлері ашылуыф мүмкін және заңды.
Шексіз көп әр алуан құрылымдар бар және олардың жиынтығын белгілі бір ретпен оқу, зерттеу математиканың әр түрлі бөлімдерінің мазмұнын құрайды.
Математика ғылымында «құрылым» терминін енгізген Н. Бурбаки барлық математиканың іргетасын құрайтын бірнеше негізгі құрылымдарды ғана анықтады.
Дәлірек айтқанда, олар бір-біріне ұқсамайтын құрылымдардың үш типін анықтады, олар алгебралық, реттік және топологиялық.
Математикалық құрылымдар аксиоматикасының мән-мағынасына тереңдемей, құрылымдардың негізгі типтерін жалпы түрде қарастырған, олар:
1) Жиындардың тобын, яғни әр түрлі сипаттағы элементтерден және онда анықталған операциялардан құралған әртүрлі жиындар. Әрбір жиынды құрайтын элементтердің табиғатына назар аудармай, осы топқа енетін кез келген жиынды А={х, у, . . . } символымен белгіленген.
А жиынында анықталған операцияны f арқылы белгілеп, А жиынына тиісті кез келген х және у элементтері үшін осы жиыннан сәйкес операцияның нәтижесі болатын z элементі табылады, яғни
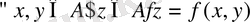
Осы қарастырылатын жиындардың әрқайсысында анықталған операциялардың барлығы үшін ақиқат болатын жалпы заңдарды көрсетсек,
Коммутативтік:
Ассоциативтік:
Қайтымдылық:
... жалғасы
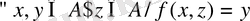
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz