Математикалық структура ұғымы, изоморфизм

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 35 бет
Таңдаулыға:

14. ЛЕКЦИЯ САБАҚТАРЫ

1 - лекция

Математикалық структура ұғымы, изоморфизм.

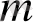1. Қатынас ұғымын еске түсірейік. Ешқайсысы бос жиын болмайтын М\, М ₂ , . . . , М _п жиындары берілсін. Кез келген Equation. 3 М _х ХМ ₂ Х . . . ХМ _п бөлімше жиын М ₁ М ₂ , . . . , М _п жиындарының ішінде анықталған n-ар (немесе п-орынды) қатынас деп аталады. Егер (т ₁ т ₂ , . . . , т _п ) Equation. 3 болса, онда т ₁ т ₂ , . . . , т _п , мұнда ( Equation. 3 Equation. 3 ^Мі) элементтері А қатынасында дейді.

Егер Мі = М ₂ = . . . = М _п -М және, сондықтан, 7MіХМ ₂ Х . . . Х ХМ _п = М ^п болса( мұнда М" дәрежесі'- М жиынының n-нші дe-карттық дәрежесі), онда т ₁ x т ₂ " n-ар катынасы М жиыны іші-де анықталған дейді.

Equation. 3 М ₁ ХМ ₂ бинар қатынас болған жағдайда (п = 2) (т _һ т ₂ ) еД орнына тіДт ₂ деп жазады.

Егер Еф0 жиыны үстінде

Equation. 3 :ЕхЕ-^Е

алтебралық операция (композицияның ішкі заңы) анықталған болса, онда оны Equation. 3 E ³ бөлімше жиын арқылы, мұнда Equation. 3 = {(а, b, с) Equation. 3 ³ Equation. 3 (а, Ь) = с} ретінде алыпа, Е жиынының ішінде анықталған тернар қатынас (п = 3) ролінде карастыруға бо-

лады.

Егер Е жиынының үстінде операторларының жиыны L бо-

латын

f:АxЕ Е

композицияның сыртқы f заңы анықталса (мультипликативтік түрде жазғанда f ( , а) = а болады), онда оны AxExE белімше жиын арқылы, = {( , а, &) AxExE \ f а = b} ретін-де алып, L, Е жиындарының ішінде анықталған тернар қаты-нас ролінде қарастыруға болады.

2. Егер біз М1ХМ ₂ Х . . . ХМ _п декарттық көбейтіндіден әр т ү р л і екі бөлімше жиын, мысалы, і мен ₂ бөліп шығарсак, онда біз М ₁ М ₂ , . . . , М _п жиындарының системасында әр түрлі екі қатынасты анықтаймыз. ₂ болғандықтан, қатына

лі бағыттарына бөлініп кететін білімдердің ұлан-байтақ саласы болып көрінетіндігіне карамастан, біртұтас ғылым. дей аламыз. . Оның зерттеу пәні - математикалық структуралар жиыны, оның негізгі әдісі - аксиоматикалық здіс.

§ 2. Аксиомалар системасының интерпретациялары (модельдері)

1. Әрбір Е жиыны үстінде кез келген структураны анықтау-
ға болады деп ойламау керек. Мысалы, Е= {0, 1, 2, 3, 4, 5}
жиыны үстінде R өрісі үстіндегі п өлшемді векторлық кеңістік
структурасын анықтауға болмайды, алайда ол структура R ^п =
= RХRХ . . . ХR (п рет) жиыны үстінде онай анықталады.

Сондықтан математикалық структураны анықтағанда Т =0 жағдайы екі себептен туады, ол себептер мынадай:

а) берілген база қажетті текті структураны құруға мүмкін-дік бермейді, бірак базаны баска бір жолмен таңдап алғаида структура құрылады;

'б) кажет структураны кұруға мүмкіндік беретін база бол-майды (база қалай алынса да, T = 0 бола береді) .

Соңғы жағдайда Т жиынын анықтайтын А, А ₂ , …. , А ₍ ак- сиомалары системасының щайшылығы бар дейді. Ал егер қа-растырылған структураны анықтайтын база болса (демек, Т 0 болса), онда ол аксиомалардың системасын қайшылықсыз дейді.

2. , ₂ , . . . , _к қатынастарына нақты мағына берерліктей
және А\, А ₂ , . . . , А аксиомалары орындалатын бір нақты М
жиыны табылды делік (демек, М ліиыны үстінде Т текті струк-
тура анықталады делік) . Ондайда А\, А ₂ , . . . , А ₍ аксиомалары
системасыньщ интерпретациясы құрылды дейді де, М жиыны-
ның езін Т текті структураның моделі дейді.

М ы с а л. М жиыны элементтері нақты сандар болатын екін-ші рстті квадрат матрицалар жиыны болісын. Әдеттегі әдіспен матрицаларды қосу және оларды й өрісіндегі нақты сандарға көбейту операцияларын қолданып, М жиыны нақты^сандардың И өрісі үстіндегі 4 өлшемді векторлық кеңістіктің моделі бола-тындығын көреміз.

Сонымен, А\, А ₂ , . . . , А ₍ аксиомалары системасының қан-шылықсыздығын дәлелдеу үшін оның әйтеуір бір интерпрета-циясып кұру жеткілікті болады.

Е с к е р т п е. Егер Т текті структураларды анықтайтын база болса, онда ол текті структуралардың А\, А ₂ , . . . , Аі аксиома-лары системасы қайшылыксыз система (басқаша айтқанда, берілген аксиомалар системасының интерпретациясын құруға болатынсистема) деп аталады дедік. Кейде аксиомалардыц мұндай системасын мағынасы бойынша қайшылықсыз система деп атайды.

Егер системадан логикалық жолмен бірі екіншісін теріске шығарарлық екі түрлі қорытынды жасалмайтын болса, онда аксиомалардың ол системасын ішкі қайшылықсыз система деп атайды.

Берілген аксиомалар системасының ішкі қайшылықсызды-ғын тексеру үшін аксиомалардан шығатын логикалық сөйлем-дердің қорытылу техиикасын зерттеу керек. Бұл мәселе мате-матикалық логиканың негізгі есептерінің бірі болып табылады. Біз бұл арада мына бір мәселені ғана атап өтеміз. Егер аксио-малар системасының мағынасы бойынша қайшылықсыз екен-дігі мәлім болса, яғни оның интерпретациясы құрылған болса, онда ол аксиомалар системасының ішкі қайшылықсыздығы жө-ніндегі проблема сол интерпретацияны құрғанда пайдаланыл-ған ұғымдар системасының ішкі қайшылықсыздығы жөніндегі мәселеге келтіріледі.

Егер бұл ұғымдар системасының ішкі қайшылықсыздығы мәлім болса, онда берілген аксиомалар системасының мағына-сы бойынша қайшылықсыздығын дәлелдей отырып, біз ол сис-теманың ішкі қайшылықсыздығын да дәлелдеген боламыз.

Сонымен, егер математикалық логика заңдылықтары арқы-лы логикалық қорытындылар шығару техникасын зерттеп қа-растырмай, тек геометрия мәселелерімен шектелсек, біз аксио-малардың берілген системасының мағынасы бойынша қайшы-лықсыздығы жөніндегі мәселені ғана шеше аламыз.

1- А\, Ач, . . . , А ₍ аксиомаларының системасы қайшылықсыз (мағынасы бойынша) және, сондықтан, негізгі қатынастары Ді, А ₂ , - . . , А _й болатын Т текті структураларды анықтайтың болсын.

М' жиыны үстінде А/ қатынастарға нақты Аі, Д ₂ , . . . , А& мағыналар берілсін де, солар бойынша А\, А ₂ , . . . , А ₍ аксио-маларының бәрі де орындалатын болсын. Сонда М' жиыны үс-тінде а'<^. Т структурасы анықталады деуге болады. Сондай әдіспен М" жиыны үстінде А/ қатынастарының нақты А^, А^, . . . , А" _һ мағыналары болатындай о"<=Т структурасы анықтал-сын. Егер

І:М'-*М"\(х'; у', . . . , о') еД; =>(Ңх'), \(у'), . . . , 1('о') ) ^А), яғни х', у', . . . , а'еМ' элементтері А қатынасында, оларға сәй. кес ] (х'), і(у'), . . . , [(о') еМ" элементтері А" _} қатынасында биекция бар болса (әдетте изоморфизм деп аталатын), онда а' және а" структуралары изоморфты структуралар деп аталады (ал М' және М" модельдері изоморфты модельдер деп ата-лады) .

М ы с а л. Т абельдік группа структурасының тегі болсын. Осы тектегі нақты екі структураны карастырайык:

' - аддитивтік группа ретінде накты сандардың R жиыны,

" -мультипликативтік группа ретінде оң сандардың R+ жиыны.

f(х) - Iп х, х R+

заңы арқылы берілетін }: К+ ->Ябиекциясын карастырайық.

Iп(ху) = Iп х+Iп у болатындықтан, f(ху) = f (х) + f (у), демек, ' және " структуралары изоморфты структуралар болады (не-месе, кейде айтылатынындай, R мен R ₊ группалары изоморф-ты группалар дейді) .

Үстінде о структурасы анықталған М жиынының өзіне-өзі-нің изоморфизмі сол жиыннын автоморфизмі деп аталады.

М ы с а л. п өлшемді векторлық кеңістік үстінде анықталған әрбір азғындамайтын сызықтық оператор сол кеңістіктің авто-морфизмі болып табылады. (Өздеріңіз тексерініздер) .

2 - лекция

Евклид және оның «Бастамалары». V постулат.

Адамдардың алғашқы геометриялық тусініктері палеолит дәуірінде (яғни жүз мыңдаған жылдарға созылған ежелгі тас дәуірінде) қалыптаса бастаған болса керек. Палеолиттің соңғы кезінде адамдар өздері паналаған мекен-үңгірлерді суреттер-мен және мүсіндермен мәнерлейтін болған. Аңшылық пен ба-лық аулаушылықтан жер кәсібіне жеткен адамдар неолит дәу-іріне (жаңа тас дәуіріне) көшкен. Бұл шамамен 10 мың жыл кейін болды. Сол кезде деревнялар бой көтеріп, қолөнер (бал-шықтан ыдыстар жасау, өрмек тоқу, ағаш ібұйымдар жасау т. б. ) мен сауда дами бастады, бұлар сан ұғымының қалыпта-суына себепші болды. Заттардың ұзындығын, бетінің ауданын және көлемін өлшеу кажет болды.

Адамдардың күнделікті практикалық қызметі кезінде біртіндеп жазықтықтағы және кеңістіктегі фигуралар жөніндегі түсініктер сараланып, фигуралардың өте-мөте қарапайьтм қа-сиеттері байқалды.

Ежелгі Вавилон мен Египеттің өте ерте замаңдағы мәдениетінің бізге жеткен ескерткіштері бүл елдерде геометрия жада-ғай эмпириялық сипатта жүріп, әр түрлі есептердің дербес жағ-дайлардағы шешімдерінің жиынтығы түрінде болғандығын көрсетеді. Мәселея, египеттіктер біздің эрамызға дейіпгі II мың-жылдықта үшбұрыштың ауданы мен дурыс тертбұрышты киық пирамиданың кәлемін дәл есептеп шығара білген.

Вавилон геометриясы да, египет геометриясы сияқты, өлшеу-ден туған практикалық есептер негізіндс дамыған. Вавилон-дықтар біздің заманымыздан бұрынғы II мыңжылдықтың езін-де «Пифагор теоремасы» деп аталған сөйлемді білген. Вавилонда астроігомия ғыльтмы елеулі табыстарға жеткен.

Ежелгі Шығыс елдерінің (Вавилон мен Египет) математикасында ешқандай дәлелдемелер болмағандығын атап айту керек, оларда тек: «есептеп шығар» дейтін жалаң ережелер ғана болған.

Біздің заманымыздан бұрынғы VII ғасырда геометрияны грек ғалымдары дамыта бастады. Аңыз бойынша, грек мате-матикасының атасы гректердің мемлекет каласы Милеттен шыққан көпес Фалес деп есептеледі. Грек көпестері Ежелгі Шығыстың математикасымен танысып, Шығыс ғалымдары теориямен жөнді шұғылданбағандығын аңғарған. «Былай есептеп шығар» дейтін іережелер бар, бірақ мынадаій сұраққа жауап жоқ: неге осылай ғана шығарамыз, дұрыс шығарғандығымызды қайдан білеміз?

Тең бүйірлі үшбұрыштың табанына іргелес бұрыштарының касиеттері жөніндегі, вертикаль бұрыштардың қасиеттері жө-ніндегі және басқа да кейбір теоремалардың дәлелдеімелерін Фалес (б. э. дейінгі 640-548 жылдар шамасы) ашқан делінеді. Фалес философтардың Ионий мектебінің негізін салушы болып табылады.

Пифагордың (б. э. дейінгі 570-471 жылдар шамасы) фило-софиялық мектебінде математика айырықша орын алған. Бұл мектептің идеялық жолын ұстағандар - пифагоршылдар - үшбұрыш бұрыштарының қосындысы туралы теореманы, Пифагор теоремасының дәлелдемесін, дұрыс көпжақтардың бес типі бар екендігін, ортақ өлшемдері жоқ кесінділердің болатын-дығын (мұны Пифагордың шәкірті Гиппас тапқан) ашқан деп есептеледі.

Демокрит (б. э. дейінгі 470-370 жылдар шамасы) дүниені затсыз кеңістікте қозғалып жүрген атомдардың жиыны деп есептеген. Атомдар (яғни «бөлінбейтіндер») - бөліктері бол-майтын, бірақ белгілі бір мөлшіерлері болатын, материалдық элементтер. Демокрит бөлінбейтіндер әдісін пайдаланып, пира-мида мен конустың кәлемдері туралы теоремаларды ашқан. Бертін бұл әдісті Архимед, Декарт, Галилей, Қавальери, қол-данған.

Пдатон (б. э. дейінгі 429-348 жылдар шамасы) әуелі гео-метриямен танысу керек, философияны содан кейін оқу керек деп үйреткен. Оның академиясының маңдайшасында мынадай, тақтайшаға жазылған, жазу тұрған: «Геометрияны білмейтін-дер мұнда кірмесін». Платонның ізбасарлары теоремалардьщ басым кепшілігін сол Платон ашқан деген. Әрине, бұл - тым асырып айтылған сөз. Платонның сіңірген еңбегі шәкірттерін ойлай білуге, логикалық іқорытындылар жасай білуге үйрету-інде жатыр, соның арқасьгнда математикалық пайымдаулардың дәлдігі мен логикалық жүйелілігі артты.

Платон кәне заман философиясында аса ірі идеалист бол-ды, Демокриттің материализміне қарсы күресті. Ол математи-када Демокриттің бөлінбейтіндер әдісін қолдануға тыйым сал-ды, онысы, сөз жоқ, математиканың дамуына бөгет жасады.

Евдокс (б. э. дейінгі 410-356 жылдар шамасы) - пропор-циялардың геометриялық теориясын жасағая ғалым, гректер иррационал сандарды білмейтін еді, бұл сандардың теориясы арқылы шешілетін мәселелер пропорциялар аркылы шешілетін еді. Сонымен қатар Евдокс тауысу әдісін ашты, бұл әдістің не-

гізгі қағидасы мынадай: «Егер А шамадан -5- А немесе одан

гөрі үлкенірек бөлігін алса, қалдығынан, тағы да солай, жар-тысын немесе одан гері үлЛетПрек бөлігін алса, осылай кайта-лап ала берсе, шамасы кез келген алдын ала берілген шамадан кіші болатын қалдыққа жетуге болады». Евдокс осы әдіспен пирамиданың, конустың және шардың көлемдерін тапқан.

Евдокстың шәкірті - Менехм конустық қймаларды ашты, бүл сызықтарды Аполлоний зор білгірлікпен зерттеді.

Аристотель (б. э. дейінгі 384-322 жылдар) - ежелгі заман-ның аса ірі философы, формальды логиканың негізін салушы. Геометриямен ол тікелей шұғылданған жоқ.

Сонымен, математика Грецияда философиямея ынтымақтаса отырып дамыды.

Б. э. дейінгі III ғасырдың басында гректерде кептеген гео-метриялық фактілер мен оларды дәлелдеу әдістерінің сұрыпта-лып жиналған мол қоры болды. Осы кезде белгілі геометрия-лық материалды түгел жинап алу және оны логикалық жағы-нан тәртіпке келтіру мәселесі көтерілді. Бұл мәселені шешуге кептеген грек авторлары (Гиппократ, Федий т. б. ) талаптанды, бірақ олардың жазған шығармалары бізге жетпей өшіп кетті, Евклидтің «Негіздері» шыққаннан кейін олар мүлде ұмыт болды.

Евклид (б. э. дейінгі 330-275 жылдар) - Платон мектебі-ніц тәрбиесін алған ғалым, кейін Александрияда математика-дан сабақ берген. Оның «Негіздерінде» геометрияның негізгі арнасы жүйелі түрде баяндалған, бұл еңбектің зор шеберлікпен жазылгандығы сонша, геометрия ғасырлар бойы осы шығарма бойынша оқытылып келген.

Епклидтің «Негіздері» 13 кітаптан (яғни тараудан) құра-лады.

- к і т а п. Үшбұрыштар туралы теоремалар, параллель тү-зулердің теориясы, үшбұрыштар мен көпбұрыштардың тең ша'-малы болу шарттары, Пифагор теоремасы.
- к і т а п. Көпбұрышты оған тең шамалы болатын квад-ратқа айналдыру.
- к і т а п. Шеңбер.

- к і т а п. Іштей және сырттай сызылған көпбұрыштар, дұ-рыс п-бұрышты салу жолдары(п = 5, 6, 10, алп = Ъжағдай 1-кітапта қарастырылған болатын) .
- к і т а п. Пропорциялар теориясы.
- к і т а п. Көпбұрыштардың ұқсастығы.

7, 8, 9 - к і т а п т а р. Геометриялық жолмөн баяндалған арифметика.

10 - к і т а п. Ортақ елшіемі жоқ шамалар.

11, 12, 13-кітаптар. Бұларда стереометрияның негіздері баяндалған, ал 13-кітап түгелімен дұрыс көпжақтар жөншдегі ілімге арналған.

Геометрияның Евклидтің тұсында ғалымдарға мәлім болған бірталай материалы (мысалы, конустық қималар теориясы, жо-ғары ретті қисық сызықтар) «Негіздерде» айтылмаған.

Әрбір кітап сол кітапта кездесетін ұғымдардың бәрінің аяықтамаларын келтіруден басталып отырады. Мәселен, 1-кі-таптың бас жағында 23 анықтама берілген. Солардың кейбі-реулерін келтірейік.

Нүкте дегеннің бөлігі жоқ.
Сызық дегеніміз ені жоқ ұзындық.
Түзу сызық дегеніміз сол сызықтың бойындағы нүктелер бойынша біркелкі орналасқан сызық.
Бет дегеннің тек ені мен ұзындығы ғана болады.
Жазықтық дегеніміз сонда жататын барлық түзулер бо-йынша біркелкі орналасқан бет.

Аныіқтамалардан кейін Евклид дәлелдемесіз қабылданатын сейлемдерді келтіреді, оларды постулаттар және аксиомалар деп екі түрге бәледі.

Постулаттар I. Кез келген нүктеден басқа бір кез кел-гей нүктеге дейін түзу сызық жүргізуге болатындығы талап еті-леді.

II. Әрбір (шектеулі) түзуді қажетіяше соза беруге болатын-
дығы талап етіледі.

Кез келген центрден кез келген радиуспен шеңбер сызуға болатындығы талап етіледі.
Тік бұрыштардың бәрінің бірдей болуы талап етіледі.

V. Әрдайым екі түзуді үшінші бір түзу қиып өткенде үшін-
ші түзудің бір жағында қосындысы екі тік бұрыштың қосын-
дысынан кем (кіші) ішкі тұтас бұрыштар құралатын болса,
шектеусіз оозғанда алғашқы айтылған екі түзудің қиылысатын-
дығы және қосындының екі тік бүрыштың қосындысынан кем
жағында -қиылысатындығы талап етіледі.

Аксиомалар I. Әрқайсысы өз алдына үшінші бір ша-маға тең екі шама біріне бірі тең болады.

II. Тең шамаларға тең шамаларды қосқанда шығатын қо-сындылар да тең болады.

VII. Бірінің орнына екіншісі дәл келетін фигуралар біріне бірі тең болады.

Содан кейін Евклид геометрияның теоремаларын баяндай-ды, бұл теоремалардың әрқайсысы бұрын қарастырылған тео-ремаларды, постулаттарды және аксиомаларды ғана пайдаланып, дәлелдеуге боларлықтай етіліп, реттелген жүйе бойынша орналастырылады.

3-5 - лекция

Гилберта аксиомалар жүйесі.

1899 ж. неміс математигі Д. Гильберттің «Геометрия негіз-демелері» атты атақты кітабы басылып шықты. Бұл кітапта тұңғыш рет евклидтік геометрияны логикалық жолмен кұруға жеткілікті болатын аксиомалардың тізімі келтірілді. Осы күнгі математикадағы а. ксиоматикалық әдіс пен математикалық структуралардың қазіргі тұрғыдан қарастырылатын теориясы (яғни Н. Бурбаки тобы қалыптастырған түсініктер) Гильберт-тің осы «Геометрия негіздемелерінен» басталады деуге болады.

Гильберттің баяндауы бойынша евклидтік кеңістік струк-турасының базасы үш жиыннан - Е, Ғ, G жиындарынан - тұрады. Бірінші Е жиынының элементтері нүктелер деп аталады да,

А, В, С, . . . , әріптерімен белгіленеді, Ғ жиынының элементтері түзулер деп аталады да, а, b, с, . . . әріптерімөн белгіленеді, G жиынының элементтері жазықтықтар деп аталады да (немесе ) әріптерімен белгіленеді.

Базаның жиындары үстінде «тиісті» (немесе жатады), «ара-сында жатады» және «конгруэнт» сөздерімен белгіленетін қа-тынастар болады. Бұл қатынастардың нақты сипаты қандай екендігі елеулі роль атқармайды, тек сол қатынастар төменде тізімі келтірілетін аксиомаларды қанағаттандыратьш болса, болғаны (бұл аксиомалар осы қатынастардың айқын тұжырымдалған қасиеттерін көрсетеді) .

Гильберт аксиомаларының тізімінде 20 аксиома бар, олар

бес топқа бөлінген.

Ітоптағы аксиомалар - іліктестік аксиомалары.

«Жатады», яғни іліктестік белгісін біз таңбасы арқылы белгілейміз. Бірінші топқа мынадай сегіз аксиома бар:

Мұндай а түзуі біреу ғана болады (ол (АВ) деп те белгіленеді) .

217

1 ₃ . Бір түзуде жатпайтын ең кем дегенде үш нүкте болады.

Егер А, В, С нүктелері бір түзуде жатпаса, былай жазып көрсетеді:

немесе немесе

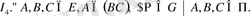
Мұндай жазықтық біреу ғана болады (ол (АВС) деп те белгі-ленеді) .

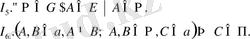
І _в . (А, В<=а, АфВ; А, В<=П, С<=а) =>С<=П.

Бұл жағдайда «а түзуі П жазықтығында жатады» дейді немесе «П жазықтығы а түзуінен өтеді» дейді.

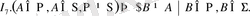
Бұл аксиомалар бойынша мынадай төореманы дәлелдеуге болады: кез келген жазықтықта бір түзудің бойында жатпайтын үш нүкте болады.

Птоптағы аксиомалар - рет аксиомалары.

Егер В нүктесі А және С нүктелерінің арасында жататын болса,

біз оны былай жазып көрсетеміз:

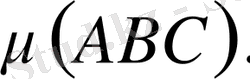
-түзудің әр түрлі үш нүктелері.

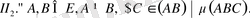
11 ₃ . Түзудің әр түрлі үш «үктесінің екеуінің арасында жата-
тывының саны бірден аспайды.

Бұдан кейін, қатынасын пайдаланып, кесінді мен оньщ ішкі нүктелерінің әдеттегі анықтамаларын және сәуленің анық-тамасын беруге болады.

11 ₄ . (Паш аксиомасы) . А, В, С нүктелері бір түзуде жатпай-
тын нүктелер, ал а түзуі (АВС) жазықтығының айтылып отыр-
ған үш нүктесінің ешқайсысынан өтпейтін түзу болсын. Егер
а түзуі кесіндісінің ішкі нүктесінен өтетін болса, онда ол
түзу [АС] кесіндісінің ішкі нүктесінен де немесе [ВС] кесінді-
сінің ішкі нүктесінен де өтеді. Айтылып отырған а түзуі [АВ],
[АС], [ВС] кесінділерінің үшеуін бірдей қиып өте алмайтын-
дығын дәлелдеуге болады.

I және II топтардағы аксиомалардан шығатын кейбір теоре-маларды көрсете кетейік.

Әрдайым түзудің әр түрлі үш нүктесінің біреуі ғана қалған ексуінің арасында жатады.
Кез келген кесіндідегі нүктелердің жиыны шексіз болады.
П жазықтығында жататынатүзуі сол II жазықтығыныңатүзуінде жатпайтын нүктелерінің жиынын екі бөлікке бөледі.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.