Математиканы тереңдетип окыту

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 80 бет
Таңдаулыға:

Математиканы тереңдетип окыту

Кіріспе

Ғылым мен техниканың даму қарқыны, экологиялық процестерді басқару теориялары күннен күнге математикалық сипат алып бара жатқаны тарихи шындық. Сонымен бірге математиканың ғылыми теорияның ізденістермен бірге практикалық қолданыстарының да ауқымының кең екені мәлім.

Екінші жағынан қуатты электрондық есептеуіш техникаларының пайда болуы, олардың өндірісте көлемді қолданылуы, техникалық экономикалық процестерді басқаруға араласуы, еңбек өнімін, экономикалық тиімділігін арттырумен қатар математикалық білімі жақсы тұлғалар дайындау қажеттігін айқындайды.

Математиканың құнды пікірлері мен әдістерін ұқыпты қолдану арқылы материалдық құндылықтарды сақтап қалуға, аурулардың алдын алуға, болжам арқылы түйінді тұжырымдамаларға келуге, жер қойнауындағы байлықтың мөлшерін анықтауға оны қолданудағы экономикалық тиімділіктерін ескертуге мүмкіндік береді.

Қоғам үшін де математиканың ролі ерекше, себебі әртүрлі бағыттағы математикалық әдістерді қолданбаса ғылыми прогрестің болуы мүмкін емес.

Осылайша, ғылым мен өндірістің біте қайнасуы ой еңбегін одан әрі жетілдіруді талап етеді. Себебі, ғылыми техниканың даму кезеңінде оқушының жалпы даму деңгейі, оның ойлауы мен өздігінен білім алу іскерлігі, алған білімін іс жүзінде қолдана алуы ерекше маңызға ие. Сондықтан ғылым негіздерін оқытып үйреткенде оқушылардың шығармашылық белсенділігін дамыту, олардың өздігінен білім алу іскерлігін қалыптастыру және оны одан әрі өрістету, алған білімін практикада қолдана білу машықтарын шыңдау бүгінгі күні зор міндет болып табылады.

Бұл өзекті мәселені жүзеге асыру күллі оқыту әдістері мен оқу тәрбие жұмысын барынша жетілдіруді талап етеді. Осыған орай математиканың қажеттілігінің артуы, математикалық білім мен біліктіліктің қолданылу аясының кеңеюі еліміздегі әрбір оқушының математикалық білімінің толық болуының мәнін және маңызын күшейте тусуде. Бұл еліміздің әрбір азаматына орта білім алуға міндет арта отырып, мұғалім қауымынан ертеңгі күні мемлекет сенім арта алатындай оқушылардың математикалық дайындығының сапасын көтеруді және білімнің қандай да бір деңгейіне кепілдік беруін қамтамасыз етуді талап етеді.

Еліміздегі математикалық білім беру өзінің даму және қайта құрылу кезеңінде өте жауапты мезгілді басынан өткізіп отыр. Оның өзектілігі 2015 - жылға дейінгі білім беруді модернизациялау тұжырымдамасында көрсетілгендей бүгінгі таңда мектептің алдына білім берудің және тәрбиелеудің сапасын жоғарылату, математика пәнін жоғары ғылыми дәрежеде оқыту талаптары қойылған. Осыған байланысты оқылатын материалдар тізбесін және көлемін нақтылау, оқулықтар мен оқу бағдарламаларындағы артық жүктемелерді алу, математика пәніндегі жетекші идея мен жетекші ұғымды нақтылы сипаттауды қамтамасыз ету, математика үшін іскерлік пен дағдының тиімді көлемін анықтау қажеттілігі туып отыр. Бұл мәселелерді шешудің негізгі бір жолы мұғалімдердің теориялық және әдістемелік шеберліктерін ұйымдастыра жетілдіру екені айқын.

Осы мақсатта ең алдымен қазіргі жұмыс істеп тұрған мектептер жұмыстарына бірлесе отырып, педагогикалық-әдістемелік ғылымдардың соңғы жылдардағы жаңалықтарын енгізуге күш жұмсауы қажет. Ал бұл жұмысты жүзеге асыру мектеп мұғалімі қауымының өз іскерліктерін арттырумен қатар олардың әдістемелік ғылым жетістіктерін меңгеруге бел шеше кірісуіне тікелей байланысты.

Сол сияқты Қазақстан Республикасы мектептерінде мамематикадан білім беру тұжырымдамасы жобасында да педагогика ғылымы мен практикасы алдына мектептегі білім мазмұны, оқыту тәсілдері, сонымен қатар оқыту процесін ұйымдастыруды жетілдіру міндеттері тұрғаны атап көрсетілген.

Осыған орай мектеп бағдарламасының көлеміндегі математиканы оқытуды ұйамдастыру мәселелері қарастырылған жұмыс ұсынылып отыр. Бұл дипломдық жұмыс математика ғылымының белгілі бір даму дәрежесіне лайық, қоғамның алға қойған оқыту мақсаттарына сай, математиканы оқытудың өзекті мәселесі - мектеп математикасын оқытуды тиімді түрде ұйымдастыруға арналған.

І - тарау. Математиканы оқытуды ұйымдастыру

1. 1. Сабақ, оның құрылымы және түрлері

Математикадан оқу жұмысын ұйымдастырудың негізгі түрі - сабақ. Әрбір сабақтың өзіне тиісті міндеті, мақсаты, бағыт-бағдары және логикалық жағынан аяқталған болуы тиіс.

Сондықтан мұғалім сабаққа даярланғанда алдымен оның мақсаты мен міндетін анықтап, оларды жүзеге асырудың тиімді жолдары мен әдістерін іздестіреді, оқу жұмысын ұйымдастырудың түрлерін таңдайды. Математиканы оқыту әдісі оқытудың түрімен және сабақтың құрылымымен тығыз байланысты, ал кейбір жағдайларда оқыту әдісі сабақтың құрылымы мен оны ұйымдастырудың түрлерін анықтап береді.

Сабақтың басты белгісі - оның дидактикалық мақсаты. Осы белгінің негізінде сабақтың типі анықталып, сарапталады. Дидактикада сабақ:

а) жаңа материалды оқып-үйрену; ә) білімді баяндандыру және ол білімді қолдана білу іскерлігі мен машықтарын шыңдау; б) өтілген материалды қайталау және жүйелеу; в) білімді бақылау және тексеру; г) құрама (комбинациялық) сабақтар болып сарапталады.

Бір типтегі сабақтардың дидактикалық мақсаты ортақ, құрылымы ұқсас болады.

Сабақ құрылымы деп оның тұтастығы мен әр алуан варианттығын, негізгі көріністерінің сақталуын қамтамасыз ететін сабақ элементтерінің жиынтығын айтады. Сабақтың құрамдас бөліктері өзара тығыз байланыста болады және белгілі тәртіпте жүзеге асырылады.

Сабақ құрылымы қойылған мақсатқа, оқу материалының мазмұнына, қолданылатын оқыту әдістері мен тәсілдеріне, оқушылардың дайындық деңгейіне және оқу процесінде сол сабақтың алатын орнына байланысты анықталады.

Сабақ құрылымы әр алуан болады. Тіпті параллель сыныптарда өткізілетін сабақтардың құрылымы бір-бірінен өзгеше болуы мүмкін. Жоғарыда көрсетілген факторларға байланысты сабақтың құрылымы ұдайы өзгеріп, сыныпқа бейімделіп тұрады. Әр сабақта әрбір мұғалімнің өзіне тән «қолтаңбасы» көрінеді.

Математиканы сабақ үстінде оқыту үрдісінің құрылымына мынадай негізгі элементтерді бөліп көрсетуге болады: 1) жаңа тақырыптың материалдарын білдіру; 2) жаңа материалды пысықтау; 3) есеп шығару, жаттығулар орындау; 4) өтілген материалдарды қайталау; 5) үйге берілген тапсырманың орындалуын тексеру; 6) үйге жаңадан тапсырма беру; 7) оқушылардың математиканы практикада қолдануы; 8) оқушылардың білім дағдыларын бақылау және бағалау.

Кез келген сабақта бұл элементтердің барлығы бірдей кездесе бермеуі мүмкін, алайда бұлардың әр түрлі комбинациясынан кез келген сабақ құруға болады. Сабақтың кейбір құрылым элементтеріне қысқаша тоқтала кетейік. Жаңа тақырыптың материалын сабақ үстінде білдіру оқушылардың өзіндік ойлау, пайымдау әрекеттерін белсенді пайдаланатындай жағдайда жүргізілуі қажет. Жаңа білімді дайын күйінде айтып беруге барынша шек қойылып, оқытушы шәкірттердің өзіндік білім алуын, дамуын ұйымдастырушы, басқарушы болу жағынан көңіл бөлу керек.

Сабақ барысында жаңа материалды игеру табиғи түрде оны пысықтауға ұласады және сонымен кезектесіп отырады. Оқытушы бағдарлама арқылы оқытуда, әдетте пысықтау бағдарламаның өзіне енгізіледі, яғни алдын ала бағдарламаланып қойылады. Проблемалық оқыту кезінде пысықтау тексерумен және проблеманы шешу нәтежесін талқылаумен қатар жүргізіледі. Эвристикалық әңгімеден кейін пысықтау айтылғаны құрғақ қайталау емес шығармашылық тұрғыда негізгі мезеттерін назар аудара айтып беруді көздеуі қажет. Проблемалық немесе жай дәрістік баяндау кезінде тек тақырыптың қиын жерлері ғана қайталанып, пысықталады.

Сабақ үстінде жаңа материалды пысықтауға, оны есептер шешіп, жаттығулар орындауға бірінші рет қолдану да жатады.

Адам психикасының табиғи бітіміндегі білгенді біртіндеп ұмытушылық қасиеті кейбір ұмытуға болмайтын негізгі мәселелерді дүркін-дүркін жүйелі түрде қайталап отыруды қажет етеді. Сондықтан да мұндай мәселелерді арнайы тапсырма ретінде берілмесе де сабақ үстінде әр түрлі формада сұрап отырған жөн болады. Мұнымен қатар сабақтың кейбір бөлігі бұрынғы өткен және жаңа материалды оқытуға қатысты мағлұматтарды еске түсіруге арналып отырады. Әрбір сыныпта жаңа материалды өтумен қатар бірінші жарты жылда өткен жылғы, ал екінші жарты жылда биылғы жылғы осы пән бойынша негізгі материалдар жүйелі түрде қайталанып отыруы қажет. Бұған әсіресе бітіруші ІХ және ХІ сыныптарда көп көңіл бөлінеді. Бұл сыныптарда жыл аяғында емтихан алдында қайталауға арнайы оқу уақыты бөлінеді. Үлкен тақырып немесе тараудан кейін жалпылаушы қайталау сабағын ұйымдастыру талап етіледі. Қайталау бір сарынды болмай, әр алуан, тартымды және шығармашылық болып, уақытты өте көп алмауы қажет. Егер жаңа тақырып бойынша теориялық материал басым болса, онда қайталауға жаттығу жұмыстарын беру қажет және керісінше. Егер жаңа материалдың көлемі үлкен болса, онда қайталауға үй тапсырмасын енгізбеу керек.

Жаңа материалды оқыту сабағы. Мұндай сабақтар әңгімелеу, баяндау немесе дәріс (лекция) әдісімен жүргізілуі мүмкін. Бірақ сабақтың кіріспесінде оқушыларды жаңа материалды қабылдауға психологиялық жағынан даярлап, олардың әрқайсысы танымдық қызметке белсене араласатындай жағдай жасау керек. Мұндай даярлық әдетте берілген материалдарды оқушыларға қайталату мен қорытындылату жолымен жүргізіледі. Мұның нәтижесінде бұрын оқылған материалдар мен мағлұматтардың арасында байланыс орнайды. Осыған орай, оқушылар ауызша немесе жазбаша үлестірмелі парақшалар бойынша жаттығу жұмыстарын орындайды.

Бұдан соң оқу міндеті қойылып, оқушылардың білімдеріне сүйеніп, логикалық талдау арқылы қойылған проблеманы шешуге кіріседі. Сабақ үстінде оқытудың баяндау, көрнекілік және практикалық әдістері біріктіріледі.

Қажетті жағдайда қойылған негізі проблеманы шағын проблемаларға жіктеуге болады. Мысал ретінде мына сабақты қарастырайық.

Синустар теоремасы (3 сағ., 8- сынып) .

Бірінші сабақта синустар теоремасын, екінші сабақта теоремадан шығатын салдарларды оқып үйренеді де, үшінші сабақта есеп шығарады. Бірінші сабақ

Төменде осы сабақтың толық мазмұнын келтіреміз. Мұнда сабақтың барлық кезеңдері және әрбір кезеңдегі жұмысты ұйымдастыру ерекшелігі көрсетіліп, сабақ мазмұны беріліп отыр.

Сабақ тақырыбы: «Синустар теоремасы».

Құрал жабдықтар: әрбір оқушыға арналған жеке тақта.

1º. Оқушылардың білімін тиянақтау . Оқушыларға қосымша дәптерлеріне орындауға арналған тапсырмалар беріледі. Мұғалімнің талап етуімен алынған жауаптарды жеке тақталарға жазып көрсетеді. Ал сынып тақтасына есеп шарттары жазылып, қажетті суреттер салынады.

1. АВС бұрышында АС = b , А = a . Мұнда а) а -сүйір бұрыш;

б) а -доғал бұрыш болғандағы h _c биіктігін табыңдар.

2. аb=mn (a, b, m, n, - нөлден өзгеше сандар) берілген. a, b, m, n , сандарынан пропорция құрыңдар. Есептің шешімі әрдайым бар ма?

2º. Синустар теоремасының практикалық қажеттілігін негіздеу.

Оқушыларға есепті шығару барысын белгілеу ұсынылады.

Егер АВ= 3см, АС=4 см, ВАС=30° болса, АВС

ұшбұрышының BC қабырғасының ұзындығын қалай табады?

Егер АВ= 3см, ВС=4 см, АС=2 см болса, АВС ұшбұрышының

бұрыштарын қалай табады?

Егер АВ= 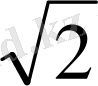, А=45°, С=30° болса, АВС ұшбұрышының ВС

қабырғасының ұзындығын қалай табады?

Егер АВ= 7, ВС=10, ВАС=60° болса, АВС ұшбұрышының С

бұрышын қалай табады?

Сонғы екі есептің шешуі (биіктігін салу және т. б. ) тиімсіз. Бұл есептерді синустар теоремасын қолданып, қарапайым жолмен шешуге болатынын мұғалім атап көрсетеді.

Бұл теореманы алғаш әзербайжан ғалымы Насиреддин Гуси (1201-

1274 ж. ж. ) дәлелдеді.

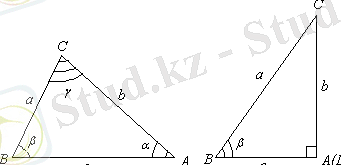
Синустар теоремасы тұжырымдалады. «Қабырғасы қарсы жатқан бұрышының синусына пропорционал» деген тұжырымнан қандай теңдік шығатыны анықталады. Тақтаға және оқушылардың дәптерлеріне сабақтың тақырыбы, теореманың шарты жазылып, сәйкес суреттер салынады ( 1-сурет) .

3º. Синустар теоремасы.

Берілгені: АВС ұшбұрышының a, b, с қабырғалары және оларға қарсы жатқан a, 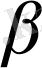, 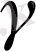бұрыштары.

Дәлелдеу керек. = = .

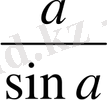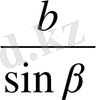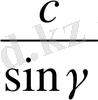Мұғалім оқушыларға 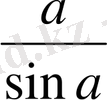= 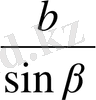теңдігін 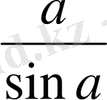= 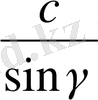теңдігін де осылай дәлелдеуге болады: 1) - сүйір бұрыш (бірінші вариант дәлелдейді), 2) a - доғал бұрыш (екінші вариант дәлелдейді) болған жағдайда өздігінен дәлелдеуді ұсынады.

Тақтаға алдын ала дәлелдеу жоспарын жазады:

СDбиіктігін жүргізіңдер.
СDбиіктігінbқабырғасы менaбұрышы арқылы өрнектеңдер.
СDбиіктігінaқабырғасы менбұрышы арқылы өрнектеңдер.
СDүшін алынған өрнектерді теңестіріңдер.

Бұл жұмысты оқушылар қосымша дәптерлерінде, ал екі оқушы тақтаға орындайды. Бұдан соң дәлелдеу талқыланып жеке оқушылардың жұмыстары бағаланады.

«Кез келген тік бұрышты ұшбұрыш үшін синустар теоремасы дұрыс па» деген сұрақ қоюға болады; бұл жағдайда СD = b=b sina, себебі а=90º (2- сурет) .

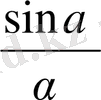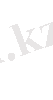
Кез келген ұшбұрыш үшін синустар теоремасын қолдануға болады деген тұжырым жасалады. Оқушыларға осы теореманы басқаша = = 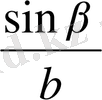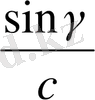немесе а:b:с=sina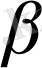: sin : sin 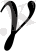түрінде де жазуға болатынын ескертуге болады.

1- сурет

2- сурет

4º. Синустар теоремасын есеп шешуге қолдану.

АВСұшбұрышындаВС=, A =45º, С =30º; АВқабырғаны

табыңдар. (Синустар теоремасын қолданып тиімді шешілген есептердің мысалын келтіруге болады) .

2) Ұшбұрыш бұрыштарының синустары 3:4:5 қатынаста болады. Бұл үшбұрыштың түрі қандай? Қабырғаларының қатынасы қандай?

3) Ұшбұрыш бұрыштарының синустары 5:7:13 қатынаста бола ма?

Үйге тапсырма: §11, 4, 12, 13.

Сабақтың келесі құрылымдық бөлігі - жаңа материал бойынша алған білімді баяндандыру және оларды іс жүзінде қолдану іскерлігін қалыптастыру. Осы мақсатта есептер шығарылып, математикалық теорияның ғылым мен техникадағы қолданысы көрсетіледі. Мұнда бүкіл сабақ бойы, оқушылардың үлгерімі мен материалды игеру дәрежесі материалды игеру дәрежесі есепке алынып отырады: бұл әсіресе жаттығулар орындалғанда және білім қорытындылағанда өте қолайлы.

Дегенмен, бұдан жаңа материалды өткенде осы құрылымды қатаң сақтау керек деген ұғым тумаса керек. Мәселен, кейбір жекелеген жағдайларда, кіріспе жаттығуларды орындамай-ақ, жаңа материалды өтуге болады. Ал, 8-10 сыныптарда оқушылар өздігінен оқулықтардан, анықтама материалдан және тағы басқа қосымша әдебиеттерден білімдерін толықтыра алады. Алайда барлық жағдайларда жаңа сабақ бұрынғы сабақтармен де, алдағы жоспарланған сабақтармен де тығыз байланыста болуы тиіс.

Егер оқу материалдары әңгімелеу әдісімен оқытылса, эвристикалық сипат басым болғаны жөн. Сабақ үстінде оқушылар өздеріне кездескен жағдайларға талдау жасап және оларды түсіндіру жолдарын іздестіруі тиіс. Сондықтан сабақты «Неге . . . ?», «Неліктен . . . ?», «Қалай . . . ?» тәрізді сұрақтар негізінде құрған жөн.

Сонымен, жана материалды оқыту сабағы: 1) кіріспе бөлім әңгіме, жаттығулар орындау; 2) проблемалық ахуал туғызу және оны шешуді ұйымдастыру; 3) табылған нәтижелерді талдау және қорытындыны тұжырымдау; 4) игерген білімді баяндандыру және қолдана білуге үйрету мақсатымен жаттығу орындау; 5) үйге тапсырма беру сияқты құрылымдық элементтерді қамтуы мүмкін.

2. Практикалық іскерлік пен машықты қалыптастыру сабағы. Математика сабақтарының мақсаты математикалық теорияларды, идеяларды, заңдар мен заңдылықтарды үйретумен бірге, оқушыларға бағдарламада көрсетілген іскерлік пен машықты қалыптастыру болып табылады. Мұндай іскерліктер мен машықтардың қатарына математикалық есептерді және практикалық мазмұндағы есептерді шығару, қарапайым есептеу құралдарын қолдану, әр алуан бақылаулар мен өлшеулерді орындау, әр түрлі модельдерді, кестелерді, диаграммаларды, табиғатта кездесетін кейбір құбылыстарды математика тіліне аудару т. б. жатады. Сондықтан бұл типтегі сабақтың негізгі бөлігін есеп шығару, лабораториялық-практикалық жұмыстар орындау құрайды. Ал практикалық іскерлік пен машықты қалыптастыру сабағының маңызды бөлігі - ұсынылған жұмысты орындау үлгісін мұғалімнің оқушыларға көрсетуі.

Сонымен, практикалық іскерлік пен машықты қалыптастыру сабағына: 1) жұмыстың мақсатын анықтау; 2) оларды орындау ережелерін теориялық негіздеу; 3) жұмысты орындау үлгісін көрсету; 4) жаттығулар орындау (бақылау, өлшеу, құралдарды қолдану) ; 5) қорытынды жасау; 6) үйге тапсырма беру сияқты құрылымдық элементтер енуі мүмкін.

3. Оқыған материалды қайталау және қорытындылау сабағы. Білімді қорытындылау мен құрылымдық элементтер сабақтың алдыңғы типтерінде де қамтылған-ды және олар білімді меңгеру процесінің элементтері ретінде көрінген болатын. Жаңа материалды бұрын өткен материалдармен байланыстыру үшін барлық сабақта қайталау қолданылады, бірақ ол информациялық материалдарды шағын көлемде ғана қамтиды. Материалды қайталау мен баяндандыру білімді практикада қолданылуға үйрету сабақтарында қарастырылады және ол мұнда да тек қажетті мағлұматтарға сүйенеді. Сондықтан мектеп математикасының жеке мәселелерінің арасында тығыз байланыс орнату үшін, білім мен іскерліктің бірегей жүйесін жасау үшін бұларға арнайы бөлінген уақыт ішінде - оқу материалын қайталау мен қорытындылау сабақтарында мұғалім мен оқушылар қосымша жұмыс істеуі қажет. Мұндай сабақтарды ұйымдастырудың түрлері әр алуан: қорытынды әңгіме өткізу, шолу лекцияларын оқу, әр түрлі есептер шешу (8-10 сыныптарда), оқу және ғылыми-бұқаралық фильмдер көрсету, арнайы оқу телехабар беру және т. б. . Сөйтсе де, мұндай типтегі сабақтардың бәрінде де, мұғалім оқушылардың білімін бір жүйеге келтіруге талаптануы тиіс.

Материалды қайталау және қорытындылау сабағы, сонымен бірге оқытылған тақырыптармен тарауларға жаңа білім элементтерін енгізуі тиіс. Мәселен, туынды ұғымын қайталағанда, оның тек физика мен механикада қолданылуын ғана емес, биология мен химияда да қолданылуын көрсетуге болады. Мұндай қысқаша мағлұматтарды мұғалім немесе оның көмегімен жеке оқушы беруі мүмкін.

Осы тарау бойынша қайталау мен қорытындылау сабағын ұйымдастыру жолдарының бірі: алдымен әңгімелеу барысында негізгі ұғымдарды анықтау; одан соң осы ұғымдарды қолданып есептер шешу; әр алуан мысалдармен мүмкіндігінше практикалық қолданысын көрсету болуы мүмкін.

Осы типтегі сабақтарды оқушылардың түбегейлі жауап беруін қаматамасыз ететіндей ұйымдастыру керек. Бұл олардың логикалық ойларын өрістетуге мүмкіндік туғызады. Сондықтан, сабақ үстінде оқушылар тек анықтамалар мен теоремалардың тұжырымдарын айтумен ғана шектелмей, тақырыптың немесе тараудың басты-басты мәселелерін жан-жақты және бірізділікпен баяндауын, жекелеген фактілердің арасындағы маңызды байланыстарды көрсетуін талап ету керек. Бұл жұмыстың басында түбегейлі жауаптың үлгілерін көрсетіп, берілуге тиісті жауаптардың толық жоспарын жасаған дұрыс.

Білімді қорытындылау мен тереңдетудің пәрменді құралдарының бірі - оқу фильмдерін көрсету. Әр тақырыпқа арналған фильмдер матеметика кабинетінде сақталуы тиіс.

Қайталау мен қорытындылау сабағының құрылымы мұғалімнің таңдаған жұмыс түріне сәйкес әр түрлі болады. Әдетте осы типтегі сабақтар: 1) қайталанатын тақырып бойынша қажетті математикалық ұғымдарды талдауды; 2) жаттығулар мен есептерді түсіндіруді; 3) оқушылардың хабарламалары мен рефераттарын талдауды; 4) тақырып бойынша оқу киноларын көрсету немесе телехабарлар беруді; 5) сабақты қорытындылауды; 6) үй тапсырмасын қамтиды.

4. Білімді бақылау және тексеру сабағы. Сабақтардың барлық типтерінде оқушылардан білімін бақылау мен бағалау жүйелі жүргізіліп отыруы тиіс. Бұл оқушылардың оқу материалын игеру деңгейін анықтауға және қолданылатын оқыту әдісінің тиімділігін тексеруге қажетті. Оқушылардың білімін ұдайы бақылау мен тексеру, оларды өздігінен оқулықпен жүйелі жұмыс істеуге, үй тапсырмасын толық орындауға, қосымша әдебиетерді ізденіп оқуға бағыттайды, жауапкершілік сезімін тәрбиелеп, өз білімін өзі бақылауға дағдыландырады, тіпті кейбір жағдайларда бағалаудың түрлері арасында сабақтастық орнатуға (мәселен, сынақ алу) мүмкіндік туғызады.

Оқушылардың білімін бақылау мен тексеру сабақтың шағын ғана құрылымды бөлігін құрайды, сыныптың аз ғана тобын қамтып, білім мен іскерліктің жекелеген түрлерін ғана қарастырады.

Оқушылардың білімін, іскерліктері мен машықтарын тексерудің негізгі түрлері - жеке және жаппай сұрақтар қою, реферат жаздыру (әсіресе жоғарғы сыныптарда), есеп шешу. Сонымен бірге, білімді бақылау мен тексеруде үй тапсырмасы мен жазбаша бақылау жұмысының, жоғарғы сыныптарда сынақ алудың өзіндік орны ерекше.

Жазбаша үй тапсырмасы мен бақылау жұмысын жүргізу, негізінен оқушылардың теориялық білімді есеп шешуге қолдану іскерліктері мен машықтарын тексеруге арналады.

Сынақ курстың маңызды тақырыптары бойынша тоқсан сайын бір рет қабылданады. Оны жүргізу үшін арнайы таратпалар дайындалып, әрқайсысына 1-2 сұрақтан, бір есептен жазылады. Сыныпты 10-12 адамнан топқа бөліп, бір топ сынақ тапсырып жатқанда, екінші топты дайындыққа отырғызу ыңғайлы, жалпы алғанда сыныпта сынақ қабылдағанда, жаппай жұмыстар жүргізілмейді.

5. Құрама (комбинациялы) сабақ. Оқу процесінде бірнеше дидактикалық міндеттері комплексті түрде шешуге тура келгенде, мәселен, үй тапсырмаларын тексеру мен өткен материалдарды қайталау, жаңа материалды түсіндіру, оны тиянақтау және т. б. қажет болғанда сабақтың ерекше типі қолданылады. Мұндай сабақтар құрама сабақтар деп аталады. Оның өзіне тән екі ерекшелігі бар: 1) дидактикалық міндеттердің тарылуы, 2) құрылымында төрт элемент (сұрақ беру, жаңа материалды оқып үйрену, білімді тиянақтау, үйге тапсырма беру) болуы.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.