Елбасы Нұрсұлтан Назарбаевтың 2012 жылғы 27 қаңтарда Әлеуметтік- экономикалық жаңғырту - Қазақстан дамуының басты бағыты атты Қазақстан халқына жолдауы

Пән: Саясаттану
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

мектеп математика курсындағы математикалық анализ элементтерін
қолданбалылық және кәсіптік бағдар бағытында оқыту

Кіріспе

Елбасы Нұрсұлтан Назарбаевтың 2012 жылғы 27 қаңтарда Әлеуметтік-
экономикалық жаңғырту - Қазақстан дамуының басты бағыты атты Қазақстан
халқына жолдауында ...оқыту қазіргі заманғы әдістемелер мен
технологияларды енгізу... . Оқу жастарға тек білім беріп қана қоймай,
сонымен бірге оларды әлеуметтік бейімделу үдерісінде пайдалана білуге де
үйретуі тиіс.
Үкіметке мектеп оқушыларының функциялық сауаттылығын дамыту жөнінен бес
жылдық Ұлттық іс-қимылдар жоспарын қабылдауды тапсырамын деп атап
көрсетті.
Инновациялық белсенділіктің жоғарғы қарқыны осы үдеріске қатысушыларды
мына шарттармен қамтамасыз еткенде ғана іске аспақшы: жаңа білім,
технология, өнім мен қызметке салынған инвестиция нәтижелеріне меншік
құқығын қорғау; инновациялар базасында бәсекелестікті кеңейту үшін
жағдайлар жасау; ұлттық инновациялық жүйенің қызмет атқару үшін қаржылық,
материалдық, еңбек ресурстарының ұтымды ұсыныстарын жасау; шаруашылық
субъектілерінің жаңашылдығына тұрақты сұранысты дамыту.
Қазақстан Республикасының Білім туралы заңында (2007 ж) білім беру
жүйесінің жеке адамды қалыптастыруға, дамытуға және кәсіби шыңдауға
бағытталған рөлі атап көрсетіліп, осы заңда: Педагог қызметкерлер
оқушылардың мемлекеттік білім беру стандартында көзделген деңгейден төмен
емес білім, білік, дағды алуын қамтамасыз етуге, жеке шығармашылық
қабілеттерінің көрініп дамуы үшін жағдай жасауға міндетті делінген.
Сондықтан, орта мектептің алдында тұрған негізгі міндеттердің бірі –
оқушылардың шығармашылық қабілетін барынша ашып, қоғамды құрып дамытуға бар
мүмкіндігін жұмсайтын қабілетті жеке тұлғаны қалыптастыру. Әрбір оқушының
тұлға ретінде қалыптасып дамуына математикалық білімнің үлкен үлесі бар.
Мектеп математикасын өмірмен байланыстыру, бұл пәнді адамдардың
практикалық және техникалық іс-әрекетіне қолдану үшін мектеп математикасы
мен математика ғылымын жақындастыру қажет.
Бұл мәселені шешу мүмкіншілігі – математикалық анализ элементтерін орта
мектеп математика курсына енгізу. Математикалық анализ элементтерін мектеп
курсында оқыту мәселесі ұзақ үдерістен өтті, оны мектепте оқыту
тәжірибесіне енгізу мәселесі XIX ғасырдың екінші жартысында-ақ көптеген
елдерді толғандырды.
ХХ ғасырдың 50 жылдарында Кеңестер Одағында математиканы орта мектепте
оқыту реформасы жүзеге асырыла бастады. Математикалық анализ элементтерін
мектеп курсына енгізу идеяларын академик Н.Н.Лузин, Д.М.Синцов, профессор
Н.А.Глаголев, Б.Н.Делоне, Я.С.Дубнов және озат мұғалімдер қолдады.
ХХ ғасырдың 70 жылдарының соңында орта мектепке жаңа курс Алгебра және
анализ бастамалары енгізілді, бұл курстың енгізілуіне байланысты осы пәнді
оқыту әдістемесін дайындаудың қажеттілігі туды.
Алғашқы кезеңде көптеген математик және әдіскерлер (А.Н. Колмогоров,
А.И. Маркушевич, С.И. Шварцбурд, Н.Я. Виленкин , О.С. Ивашев-Мусатов және
тағы басқалар) курстың жетекші идеясы мен мазмұнын анықтау бағытында жұмыс
жасады.
Орта мектепте математикалық білім мазмұнын жетілдіру, математикалық
білімнің сабақтастығы мен болашағы мәселелері қазақстандық ғалымдар А.Е.
Әбілқасымова, М. Есмұхан, Б. Баймұханов, Е.Ө. Медеуов,С.Е. Шәкілікова, Н.
Темірғалиев,Ә.Б. Тұңғатаров, Ә. Қағазбаева тағы басқалардың еңбектерінде
қарастырылды.
Сонымен қатар Қазақстан Республикасы мектептеріндегі математиканың
қазіргі мазмұнына талдау жасайтын болсақ, онда көптеген тақырыптардың
немесе жеке бір теориялық материалдардың не үшін оқылатындығы оқушылар
емес, кейбір жағдайда мұғалімнің өзіне де түсініксіз болып қалады.
Сондықтан көптеген оқушылардың математиканы оқып білуге деген ынтасы
төмендеп, қызығушылық танытпайды. Сондай тарауларың бірі орта мектептегі
математикалық анализ курсының элементтері.
Орта мектеп курсына математикалық анализ элементтерін енгізу
математиктер, әдіскерлер мен мұғалімдердің алдына біршама қиын мәселелер
қойды. Оқушылардың функцияны зерттеудегі білім мен тәжірибесін жетілдірудің
тиімді тәсілдерін дәл айқындап, біліміне бағыт беруде үлкен қиындықтар алып
келді. Мысалы, туындының формулаларын таныстырудан бұрын, оның анықтамасын
дәл мағынасын да түсіндіре білу, меңгеру қажет. Сондықтан да зерттеу
тақырыбын Мектеп математика курсындағы математикалық анализ элементтерін
қолданбалылық және кәсіптік бағдар бағытында оқыту деп атадық.
Зерттеу объектісі: орта мектепте математикалық анализ элементтерін
оқыту үдерісі.
Зерттеу пәні - орта мектепте математикалық анализ элементтерін
қолданбалылық және кәсіптік бағдар бағытында оқыту әдістемесі.
Зерттеудің мақсаты – орта мектепте математикалық анализ элементтерін
қолданбалылық және кәсіптік бағдар бағытында оқыту әдістемесін жетілдірудің
ғылыми-әдістемелік жүйесін айқындау және практикалық мазмұнды жаттығуларды
жүйелеуді жүзеге асыру.
Зерттеудің міндеттері:
- орта мектепте математикалық анализ элементтерін қолданбалылық және
кәсіптік бағдарда оқытуды жетілдірудің философиялық, әлеуметтік,
психологиялық-педагогикалық және әдістемелік алғы шарттарын
айқындау;
- математикалық анализ элементтерін оқытудағы пәнішілік және пәнаралық
байланыстарды жүзеге асыру;
- орта мектепте математикалық анализ элементтерін оқытуды қамтамасыз
етуге бағытталған ғылыми тұрғыдан негізделген оқу-әдістемелік жүйе
жасау;
- орта мектепте математикалық білім беру жүйесіндегі сабақтастықта
математикалық анализ элементтерін қолданбалылық бағытта оқытудың
орны;
- жасалған әдістемелік жүйенің тиімділігін тексеру үшін эксперимент
жүргізу, оның нәтижелерін қорыту және бағалау.
Зерттеу жұмысының болжамы:
егер орта мектепте математикалық анализ элементтерін қолданбалылық және
кәсіптік бағдар бағытында оқытудың әдістемелік жүйесін жасап, оларды оқыту
үдерісіне қолдансақ, онда математиканы оқытудың тиімділігі артады, ойлау
қабілетін қалыптастыруға мол мүмкіндіктер туады, бәсекеге қабілетті жеке
тұлға тәрбиелеудің негізі қаланады, себебі оқушылардың математикалық білім
деңгейі көтеріледі, өмірге бейімділігі артады.
Зерттеу жұмысының теориялық және әдістемелік негіздері:
Таным, білім, жеке тұлға және оның іс-әрекеті, ақыл-ой, құндылық туралы
философиялық, психологиялық, педагогикалық теориялар мен тұжырымдамалар,
білім сапасы теориялары.
Зерттеу көздері: Қазақстан Республикасы 2015 жылға дейінгі білім беруді
дамыту Тұжырымдамасы, Қазақстан Республикасы жалпы білім берудің
мемлекеттік жалпыға міндетті стандарттары, пәндік оқу бағдарламалары, оқу-
әдістемелік кешендері, мұғалімдердің, диссертанттың педагогикалық
эксперимент нәтижелері.
Зерттеу әдістері: қарастырылып отырған мәселелерге байланысты
психологиялық, педагогикалық және әдістемелік еңбектермен оқып танысу және
оларға талдау жасау; математика пәні бойынша жасалған оқу бағдарламаларын,
оқулықтарды талдау; математикалық білім беру жөніндегі озат педагогикалық
тәжірибелермен танысу және жинақтау; оқушылардың оқу сапасының нәтижесін
талдау, тәжірибелік-эксперименттік жұмыс жүргізу және қорытындылау.
Зерттеу базасы: Қызылорда қаласындағы № 9 мектеп-гимназиясы.
Зерттеу жұмысының ғылыми жаңалығы:
- орта мектепте математикалық анализ элементтерін қолданбалылық және
кәсіптік бағдар бағытында оқытуға талдау жасалынды;
- математикалық анализ элементтерінің ұғымдарын енгізу мен
қалыптастыру психологиялық-педагогикалық тұрғыдан негізделіп,
компоненттері анықталды;
- математикалық анализ элементтерін қолданбалылық және кәсіптік бағдар
бағытында оқытуда пәнішілік және пәнаралық байланыстар жүзеге
асырылды;
- орта мектепте математикалық анализ элементтерін қолданбалылық және
кәсіптік бағдар бағытында оқытуда компьютерлік технологияны қолдану
және математикалық лабораториялық жұмыстар жүргізу арқылы
жетілдірудің әдістемелік жүйесі дайындалды.
Зерттеу жұмысының теориялық маңыздылығы: оқушының бәсекеге қабілетті
жеке тұлға ретінде қалыптасуы шарттарының бірі ретінде мектеп математика
бағдарламасындағы материалдар болашақ мамандақтарға сай өндірістік
техникалық, ауылшаруашылық, экономикалық және гуманитарлық мазмұнды
есептермен байланысты болуы қамтамасыз етудің жолдары қарастырылып,
жүйеленіп оны жүзеге асыру жолдары белгіленді.
Зерттеу жұмысының практикалық маңыздылығы:
- мемелекеттік стандартқа сай математикалық білім алуда қолданбалылық
және кәсіптік бағдар беруді қалыптастыру үшін математикалық анализ
элементтері бойынша пәнаралық және пәнішілік байланыстарды,
қолданбалылық бағыттағы есептер жүйесі сабақтастыққа сәйкес жүйеленіп
дайындалды;
- қолданбалылық есептерді математикалық анализ тәсілдерін пайдалана
отырып, олардың артықшылығы мен жетістігін көрсету арқылы оқушылардың
жалпы математиканы іс-жүзінде қолдана білу әдістемесін орта мектепте
игертуді жүзеге асыру үшін практикалық қолданыс деңгейіне жеткізілді.
Зерттеу нәтижелерін орта мектепте, көп салалы орта оқу орындарында,
орта кәсіптік мектеп-лицейлерде математикалық анализ элементтерін оқыту
барысында және оқу-әдістемелік кешендер мен бағдарламалар дайындауда
пайдалануға болады.
Зерттеу нәтижелерінің дәлелділігі мен негізділігі: зерттеу проблемасына
сәйкес психологиялық, педогогикалық, математикалық, әдістемелік
әдебиеттерге және нақтылы тәжірибеге терең талдау жасалынуымен, зерттеу
проблемасының қойылуы, зерттеу мазмұнының ғылыми талапқа сай келуімен,
зерттеу пәніне сәйкес тиімді әдістер, құралдар, қазіргі технологияны
қолдану, оны жүзеге асырудың логикалық тұрғыдан жүйелілігімен,
эксперименттік жұмыстың оң нәтижелерімен, қойылған зерттеу болжамының
дәлелденуімен қамтамасыз етіледі.
Қорғауға ұсынылатын қағидалар:
- математикалық анализ элементтерін қолданбалылық және кәсіптік бағдар
бағытында оқытудың мүмкін жолдарын қамтитын тұжырымдама оны оқыту
әдістемесін жетілдіруге теориялық, ғылыми әдістемелік негіз бола
алады;
- математикалық анализ элементтерін қолданбалылық ұғымдарын енгізу мен
қалыптастыру компоненттері білім сапасын көтеруге оң әсерін тигізіп,
оқушылардың математикаға қызығушылығын туғызады;
- математикалық анализ элементтерін қолданбалылық және кәсіптік бағдар
бағытында оқытуда пәнішілік және пәнаралық байланыстарды жүзеге асыру
білім сапасын арттырады;
- орта мектепте математикалық анализ элементтерін қолданбалылық және
кәсіптік бағдар бағытында оқытуды жетілдірудің әдістемелік жүйесі
білім мазмұнына енгізілген таңдау және арнайы курстар, сыныптан тыс
жұмыстар мен компьютерлік технологияны қолдану арқылы жүзеге асырылды.
Зерттеу нәтижелерін сынақтан өткізу және іс тәжірибеге ендіру. Зерттеу
жұмысының негізгі қағидалары ғылыми баяндама түрінде Қорқыт Ата атындағы
Қызылорда мемлекеттік университетінде өткен Ғылым, білім және инновация:
жастардың ғылыми шығармашылығы атты жас ғалымдар конференциясында (2011
ж.), Болашақ университетінің 15 жылдығына арналған Аймақтық инновациялық
дамудағы бизнес пен білімнің әріптестігі атты республикалық ғылыми-
тәжірибелік конференциясында (2010ж), Алматы қаласында өткен Орта мектеп
пен жоғары оқу орындарындағы математика курсы мазмұнының сабақтастығы
мәселелері тақырыбында өткізілген республикалық семинарында (2011ж),
Математика және математиканы оқыту әдістемесі кафедрасының семинарында
(2011, 2012 ж.ж.), осы университеттің Білім және ғылымның инновациялық
дамуы: бәсекеге қабілетті мамандар даярлаудың проблемалары мен болашағы
атты халықаралық ғылыми-тәжірибелік конференциясында (2011ж) талқыланды.
Қызылорда қаласының №9 мектеп-гимназиясының іс-тәжірибелеріне енгізілді.
Диссертациялық жұмыстың құрылымы мен көлемі. Диссертация кіріспеден,
екі тараудан, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады.
Кіріспеде зерттеу тақырыбының көкейкестілігі, объектісі, пәні, мақсаты,
міндеттері, зерттеу әдістері, болжамы, зерттеу көздері мен базасы,
диссертацияның теориялық және практикалық маңыздылығы, ғылыми жаңалығы және
қорғауға ұсынылатын қағидалар баяндалады.
Орта мектепте математикалық анализ элементтерін қолданбалылық және
кәсіптік бағдарда оқытудың ғылыми негіздемелері атты бірінші тарауда орта
мектепте математикалық анализ элементтерін қолданбалылық және кәсіптік
бағдарда оқыту барысында оқушылардың шығармашылық қабілетін дамытудың
психологиялық-педагогикалық ғылыми негіздері қарастырылады. Оқу
процесіндегі математикалық анализ есептерінің орны мен ролі; есептерді шешу
процесінде оқушылардың қолданбалы бағыттағы ойлауды қалыптастырудың іс-
әрекетін басқару құрамы анықталады.
Мектептегі оқу бағдарламасындағы математикалық анализ элементтерінің
негізгі сұрақтары атты екінші тарауда математикалық анализ курсындағы
есептерінің орны мен ролі, практикалық мағынасы бар және әртүрлі өмір
проблемасынан, адамның күнделікті қажеттілігінен туған есептер арқылы,
сонымен бірге Maple компьютерлік бағдарламасы арқылы оқушылардың
шығармашылық қабілетін қалыптастыру және дамыту әдістемесі қарастырылады.
Үшінші тарауда педагогикалық эксперимент жұмысы, оның барысы мен сандық-
сапалық өңдеулері мен көрсеткіштері келтіріліп, зерттеу болжамының
дұрыстығы көрсетіледі.
Қорытындыда жүргізілген зерттеу жұмысының негізгі нәтижелері
тұжырымдалып, математикалық анализ элементтері есептері негізінде
оқушылардың шығармашылық қабілетін жетілдіруге қатысты ұсыныстар беріледі.
Жұмыстың негізгі мазмұны

Математиканы қолданбалы бағытта оқыту дегеніміз – математиканы
оқытуда техника мен оған жақын ғылымдарда оны қолдану, халық шаруашылығы
мен тұрмыста қолдануға бағыттау немесе оқытуға техникалық бағыт беру, яғни
физика, химия, биология, география, сызу, технология сабақтары курсымен
байланыс орнату, компьютерлік сауаттандыру, математикалық ойлау және жұмыс
дағдысын қалыптастыру, оқушыны есептер шешуге, мысалдар шығартуға, оқушы өз
бетінше есептей білу дағдысын қалыптастыру.
Қолданбалы есептерді шығару оқушылардың басқа пәндерді оқып білуге,
еңбек барысында, күнделікті өмірде математиканы қолдана білуге қажетті
білімдер, іскерліктер мен дағдыларды қалыптастыруға септігін тигізеді.
Кейбір жағдайларда қолданбалы есептерді шығару барысында көптеген
мұғалімдер ол есептің математикалық моделін құруға, мысалы, теңдеу құруға
оны шешуге көбірек назар аударады. Әрине бұл дұрыс. Бірақ та мұндай
есептерді шығару сан жағынан аз болса да, ол есептердің бастапқы берілген
шарттарын талқылауға, оларда берілген шамалардың мән-мағынасын анықтауға,
сондай-ақ ол есепті шешудің таңдап алынған жолын және құрылған
математикалық модельдің дұрыстығын анықтап талдауға аса назар аудару қажет.
Өйткені, қолданбалы есептерді шығару барысында бұл мәселе оқушыларда үлкен
қиындық тудырады. Және де оқушыларда қолданбалы бағыттағы ойлауды
қалыптастыруға үлкен әсерін тигізеді.
Математиканы қолданбалы оқыту үшін мұғалім сабақ барысында қолданылатын
әдістерді, оқыту құралдарын, әр сабақтың мақсатын - бәрін осыған бағыттауы
керек.
Математикалық білім беруде пайдаланылатын қолданбалы сипаттағы
есептер жүйелерін жетілдірудің басты ерекшеліктері:
- математикалық білім берудің мақсаттары мен міндеттерін іске асыруға
бағытталған практикалық әрекет пен үздіксіз білім беруде
пайдаланылатын қолданбалы сипаттағы есептер мазмұнының арасындағы
бірлікті, осы есептердің мазмұнын жаңартуды экологиялық,
республикалық, ұлттық-аймақтық материалдар пайдалану арқылы іске
асыруда жүйелілік, үздіксіздік, пәнаралық принциптерді басшылыққа алу;
- математика сабағында экологиялық білім мен тәрбие беру көбінесе,
табиғатты тиімді пайдалану идеясын және экологиялық мәселелердің
әлемдік мәнін сипаттайтынын ескеру;
- қоғам талабына сай білім беруде математикалық білімнің адамдардың
қоршаған ортада, мәдени құндылықтар айдынында еркін бағдарлай алуына
әр түрлі ақпарлар ағынында өзіндік баға бере алуына мүмкіндік беретін
маңызды құрал екендігінің ескерілуі.
Мұндай жетілдіру математикалық білімнің сапасы мен оның күнделікті өмірдегі
қолданымын, сабақ тиімділігін арттыруға, табиғатты негізгі байлық деп
түсінуге көмектесетін экологиялық, экономикалық білім мен тәрбие беруге,
яғни математикалық білім беруді ізгілендіруге мүмкіндік береді.
Есептің жүйесін жетілдірудің жетекші бағыттары:
1) есеп мазмұнындағы ақпараттардың жаңалығы;
2) пәнаралық байланыстың сақталуы;
3) есеп мазмұнының оқушыны қызықтыратындай болуы, яғни есеп мазмұнына
пайдаланылған материалдың оқушы өміріне етене жақындығы;
4) есептердің қолданбалы бағыттағы, олардың өмірде өзіндік мәнділігі;
5) есеп мазмұнының тәрбиелік маңыздылығы;
Есептердің қолданбалы бағытына қарай бірнеше түрге бөлуге болады. Олардың
біріншісіне, яғни ең төменгі деңгейіне қажетті математикалық модельді
құруға керекті мәселелер есептің шартында тікелей беріледі. Мұндай
есептердің таза математикалық есептерден айырмашылығы ондағы шамаларға
қандай да бір мазмұнды мағына беріледі. Мектеп курсында мұндай есептер
қарапайым теңдеулер құруға берілген практикалық есептер болып табылады.
Екінші деңгейіне, оқушылар оларды шешу барысында есептің шартында
айтылмаған, бірақта өте қарапайым, адамдардың күнделікті өмірінде
кездесетін математикалық тәуелділіктерді (мысалы, заттың құны, бағасы және
саны арасындағы, дененің бірқалыпты қозғалысындағы жылдамдық, уақыт және
жүрілген жол арасындағы тәуелділіктер т.б.) қолдану арқылы шығарылатын
есептер.
Үшінші деңгейдегі түріне, оқушылар оларды шығару үшін басқа пәндерді
(физика, химия, биология және т.б.) оқып, білу барысында меңгерген қандай
да бір заңдылықты немесе оқулықтан, ия болмаса анықтамадан белгілі бір
материалды тауып қолдану арқылы шығарылатын есептерді жатқызамыз.
Төртінші деңгейдегі түріне, оқушылар есептерді шығаруды жеңілдету
үшін қандай да бір ұйғарымдар жасауға немесе есепті шығаруға онша маңызды
емес мәселені ескермейді, ия болмаса, артық берілген мәліметтерді
қарастырмайды, ал жетіспейтін материалдар болса, оларды тауып есеп шартымен
қосып қарастырады. Мұндай есептерді шығару барысында оқушылар күнделікті
өмірде кездесетін қиыншылықтарды шешуде жақын жағдайда болады. Есеп шығару
мұғалімнің басшылығымен жүзеге асуы қажет.
Ең жоғары дәрежедегі бесінші деңгейіне нақты бір физикалық обьектіге
немесе құбылысқа байланысты мәселелер жатады.
Бірақ математика практиканың дамуына, оның проблемаларын шешуде
қандай көмегін тигізетінін көрсету үшін, ойдан құрастырылған есептер емес
шын мәнінде тікелей әртүрлі өмір проблемасынан есептер, адамның күнделікті
қажеттілігінен туған есептерді шешіп көрсету қажет.
Сол мақсатта төменде өмір қажеттігінен туындаған есепті көрсетейік.
№1 есеп. Жайылымдағы сиырларға жем беретін астауларды орын ауыстыруға
жеңіл болсын деп оларды бірдей үш тақтайдан бір-бірімен доғал бұрыш
жасайтындай етіп шегелеп құрастырады. Астауға барынша көп жем кетуі үшін
екі жақтауының табан жазықтығымен жасайтын бұрышы қандай болуы керек.
Шешуі: Тақтайдың енін 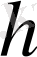деп, ал 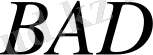бұрышын (1-сурет) деп
белгілейік. Сонда
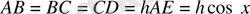
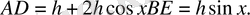
Астаудың формасы-табаны болатын, биіктігі тақтайдың ұзындығына
тең призма. Тақтай ұзындығының өлшемі 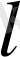деп белгілеп, призманың көлемін
табайық.

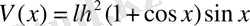
Ендігі сұрақ 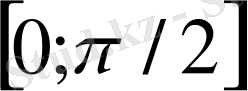аралығының 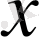қандай мән қабылдағанда 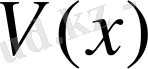функциясы
ең үлкен мән қабылдайды.
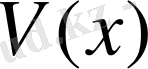функциясының туындысын табамыз.

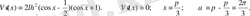
Сонымен бірге математикалық анализ элементтерін қолдануда Maple
компьютерлік бағдарламасын пайдаланып жұмыс жасау оқушылардың математика
пәніне деген, есеп шығаруға деген ынтасын, қызығушылығын арттыруға зор
ықпалын тигізеді. Себебі, бұл бағдарлама арқылы күрделі келетін
функцияның, оның туынды функциясының графиктерін жылдам және сапалы
орындау, есептің нақты және дәл шешіміне оңай әрі тез жетуге болады.
Оқушы Maple бағдарламасында тек функцияны зерттеуді ғана емес, сонымен
қатар барлық функциялардың графиктерін көрнекі түрде салып, олардың
қасиеттерін толық игеруіне болады.
Maple жүйесінде бірінші ретті туынды бойынша функцияның экстремумдарына
мысалдар қарастырайық.
№2 есеп. 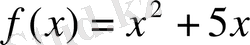функциясының экстремум нүктелерін табайық.
(2-сурет).

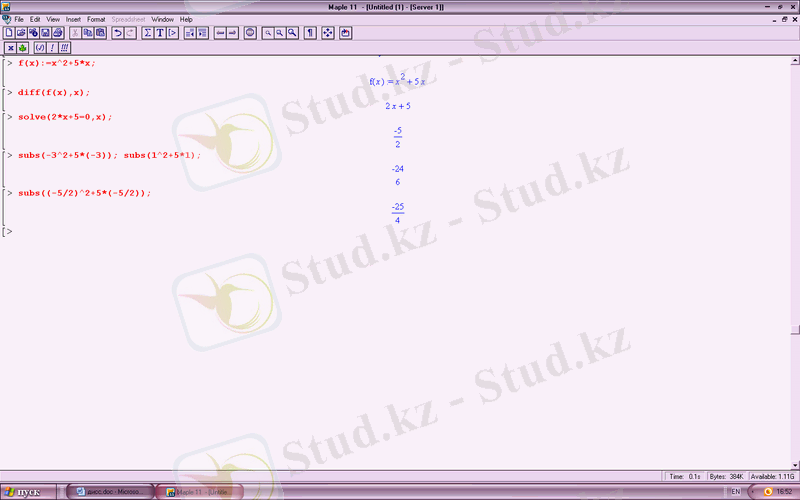
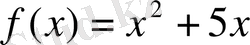функциясының бірінші ретті туындысын тауып, табылған туындыны
нөлге теңестіре отырып 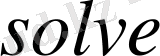операторының көмегімен функцияның кризистік
нүктелерін табамыз. Шыққан нәтижеден, берілген функцияны мына аралықтарда
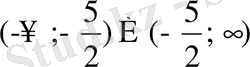зерттейміз. Ол үшін функцияның үздіксіз екендігін ескере отырып әр
аралықтарда жататын мәндерді функцияның айнымалысының орнына қоя отырып
тексереміз. Бұл процесті орындауға Maple бағдарламасының subs операторын
пайдаланамыз. Мұндағы subs– тексеру операторы. Енді функцияның кризистік
нүктелеріне толық көзімізді жеткізу үшін, геометриялық кескінін береміз (3-
сурет).

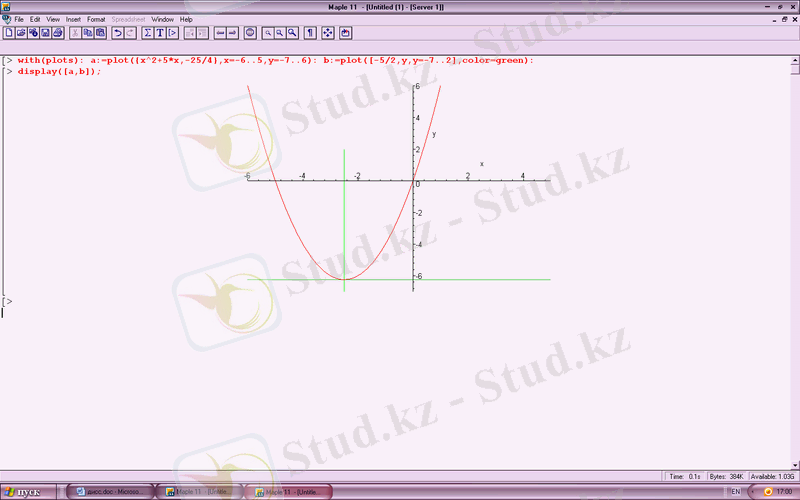
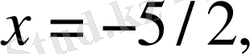
Функцияның графигінен анық көрініп тұр. Яғни, 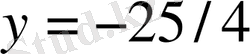нүктелерінің
координаттары 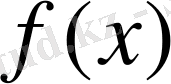функциясының минимум нүктесін береді.
Зерттеу барысындағы ой тұжырымдар мен болжауларды нақтылауға
тәжірибелік эксперимент Қызылорда қаласының №9 мектеп-гимназиясында өтіп,
оған 32 оқушы қатысты.
Эксперимент жұмысының міндеттері мынадай болатын: оқушылардың жалпы
математикалық анализ элементтерінің есептерін шешу принциптері мен
методтарын қолданып математикалық анализ есептерін шешу дағдыларын,
оқушылардың танымдық дамуын қалыптастыру, ойлаудың диалектикалық стилін
дамыту.
Негізгі мақсат – алдымен оқушылардың математикалық білімдерінің
сапасын, математикалық ойлау қабілетінің деңгейін анықтау және осы тұрғыда
мұғалімдер тарапынан жүргізіліп жатқан жұмыстардың бағытын анықтау болды.
Жазба жұмыстары алынып, оларға талдау жасалды. Сондай-ақ, мұғалімдермен
әңгіме-кеңес, оқушыларға сауалнама жүргізіліп, нәтижелері диссертацияда
берілді.
Іздену экспериментінде оқушылардың бір айнымалылы функцияны зерттеуге
қалыптастыру мақсатында графиктік есептер жүйесіне енетін есептердің
мазмұнына қойылатын талаптар анықталып, зерттеудің әдістемелік тәсілдерін
жинақтау, оларды талдау жұмыстары жүргізіліп, соған сәйкес тұжырым
жасалынды.
Сауалнамалық сұрақтар жартылай ашық түрде болды, сұрақтардың басым
көпшілігіне жауаптар ұсынылды және ешқандай шектеу қойылған жоқ. Егер
ұсынылған сұрақтардың жауаптары жауап берушіні қанағаттандырмаса, онда
оқушыға өз нұсқасын қосып тіркеп жазуға мүмкіндік берілді.
Осы сауалнаманың қорытындысы келесі диаграммада көрсетілген.

4-сурет – Анкетаның қорытындысы (% бойынша)
Зерттеу жұмысының алдында бақылау және эксперименттік топтардан
оқушылардың математикалық анализ есептерін шығару қабілеттерінің даму
деңгейін анықтау мақсатында өзіндік жұмыс алдық. Өзіндік жұмыс 3 есептен
тұратын бақылау жұмысы. Бұл оқушылардың тек математикалық объектінің
танымдық мүмкіндігін ғана анықтау мақсатында емес, сонымен қоса, олардың
шығармашылық қабілеттерін анықтау негізінде математикалық анализ
элементтерімен жұмыс жасай алуын анықтауға бағытталды. Бақылау және
эксперименттік сыныптардың оқушылары эксперимент алдында дәстүрлі
әдістемемен оқытылғандықтан, өзіндік жұмыс тапсырмалары өтілген
материалдарды қайталау негізінде алынды.
Орындалған жұмыстан оқушылардың шығармашылық қабілеттерінің даму
деңгейі бойынша бақылау және эксперименттік сынып оқушыларының бағалануы
келесі 1-кестеде көрсетілген.
1-кесте. Бақылау және эксперименттік сынып оқушыларының математикалық
қабілетінің деңгейлері бойынша экспериментке дейінгі көрсеткіштері

Сыныптар Оқушылар бір айнымалының функциясын
саны зерттеуді ойлау қабілеттерінің
деңгейі
жоғары орташаданорташа Төмен
жоғары
Бақылау сыныбы 16 3 5 6 2
Эксперименттік сынып 16 3 4 7 2

Көріп отырғанымыздай, екі сынып оқушыларының деңгей көрсеткіштері
бойынша бөлінген топтамаларының айырмашылықтары өте аз. Оқушылардың бір
айнымалылы функциясын зерттеу деңгейінің жіктелулері пайыздық көрсеткіш
бойынша келесі кестеде келтірілген.
2-кесте. Экспериментке дейінгі оқушылардың білім деңгейлерінің пайыздық
көрсеткіштері.

Сыныптар бір айнымалының функциясын зерттеуді ойлауды
дамыту деңгейі (% бойынша)
жоғары орташадан орташа төмен
жоғары ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.