Монте-Карло әдісі және имитациялық моделдеу: сызықты алгебралық теңдеулерді шешу мен геологиялық қорларды бағалау


Мазмұны
Кіріспе . . . 3
І бөлім. Монте-Карло әдісіне толық түсінік және оның
қолданылу жолдары
- Монте-Карло әдісін қолдана отырып, имутациялық
моделдеуге түсініктеме беру . . . 5
- Имутациялық модельдеудің имутация өндірісінде
Қолданылуы әдістері . . . 9
ІІ бөлім. Сызықты алгебралық теңдеулер жүйесін Монте-Карло
әдісімен шешу.
2. 1. Монте-Карло әдісінің имутациялық модельдеуге
тигізер пайдасы . . . 13
2. 2. Сызықты алгебралық теңдеулер жүйесін пайдаланып, геологиялық
артықшылықтарды бағалау . . . 17
Қорытынды
Қосымша
Пайдаланылған әдебиеттер тізімі
Кіріспе
Зерттеу барысында көптеген аналитикалық және де статистикалық әдістер қолданылады. Осылардың әрбір түрінің кемшілігі де, артықшылығы да бар. Аналитикалық модел өте қиын, күрделі болғанымен, ол факторлардың санының аздығын толықсыздығын талап етеді. Бірақ оның нәтижесі әрі нақты, әрі заңды болады, ал ең бастысы аналитикалық модель оптималдық шешімді табуға өте қолайлы. Статистикалық модель - аналитикалық модельге қарағанда өте қарапайым, әрі дәл нәтиже ала отырып, аналитикалық модель секілді аз факторларды талап етпейді.
Бірақ та екі модельдің де өзі тән кемшіліктері бар. Олар: көп уақытты талап ету оптималды шешімді шешу барысында кездесетін қиындықтар және т. б.
Зерттеу барысында ең тиімді әдіс - осы екі модельді қатар қолдану. Аналитикалық модель жалпы мәселені талқыласа, ал статистикалық модель нақтылықты анықтайды.
Имутациялық модельдеу заман талабына, адамдардың ой-өрісінің дамуына байланысты процестерде қолданылады.
Операцияны басқарушы адам көптеген қиындықтарға тап келгенде белгілі бір шешім қабылдауға мәжбүр. Мысалы шахматист тақтаға қарай отырып, өзіне тимді әдісті таңдайды. Одан соң математикалық модель іске кіріседі. Оның көмегімен іс-әрекет барысында кездесетін өзгерістердің шешімі анықталады.
Келесі шешім нақты есептің барысымен анықталады. Іс-әрекетті басқарушы адам бірнеше іс-әрекеттерді қайталаудан соң, өзінің, өзгенің жіберген қателіктерінен соң, нақты, дұрыс, өзіне тиімді шешімді оптималды немесе оптималды емес шешімді қабылдайды.
Курстық жобаның мақсаты : Басты мақсат өзіндік іздену жолдарын қарастыру. Компьютерлік бағдарламаны пайдалана отырып, берілген есептің нәтижесін шығару. Осы есептің мазмұнын анықтауға, әдістер мен формаларын қарастыра отырып, оқыту құралы ретінде қарастыру. Есепті шығарудағы белсенділік, ойлана білу, дербес еңбектің соңына жетуге дағдылану.
Зерттеу пәні : Өндірістік және эконлмикалық процестерді модельдеу
Зерттеу әдістері : Ғылыми оқулықтар, журналдар, интернет желісі.
Курстық жобаның құрылымы: кіріспеден, екі бөлімнен, қосымша және пайдаланылған әдебиеттер тізімінен тұрады.
І бөлім. Монте-Карло әдісіне толық түсінік және оның
қолданылу жолдары
Монте-Карло әдісін қолдана отырып, имутациялық
моделдеуге түсініктеме беру
Интегралдарды есептеуді қайталану алгоритмі және бағдарламасы бойынша анықтауға болады, өткен бөлімдерде көрсетілгендей. Алайда интегралдың кенеттен өсуі сандық іс-әрекетті арттырады. Статистикалық әдіс кемшіліксіз болмайды. Монте-Карло әдісінің теориялық негізі жайында кітапта жазылған.
Бұл жерде біз Монте-Карло әдісінің екі нұсқасы интегралдарды есептеуге арналған. Бірінші әдісін интегралдарды статистикалық әдіс бойынша анықтауға болады. Х 0 - кез келген сан, интеграл [а, в] аралығындағы сандарды қабылдайды. N санын тексере келе х і -дегі мәнді интегралдың жуық мәні деп аламыз.
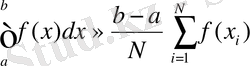
N саны өскен сайын, интеграл кеми түседі мына E~N -1/2 заңдылық бойынш.
Жоғарыда келтірілген формула қысқаша интеграл үшін
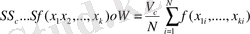
Мұндағы V с - k - интеграл облысындағы өлшемді көлем. Сандардың түйіндісі Е -2 функциясына пропорционал.
Екі қадам бойынша Монте-Карло әдісі
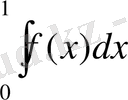 интегралы үшін, мұндағы
интегралы үшін, мұндағы
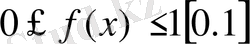 интервалына тең.
интервалына тең.
Сонда х і , у 1 остерін бір квадраттың ішіндегі нүктелер деп қарастыруға болады. Нүктелердің квадрат ішінде тең орналасуына байланысты S нүктесі y=f(x) функциясына, ал жалпы шығын N
J = S/N
Бұл алгоритм қысқа интегралға да арналған.
Бағдарламада Монте-Карло әдісінің 2 нұсқасы интегралды анықтау үшін берілген.
Неігзі бөлімде әрбір бағдарламада нұсқасының нөмері, N сандар, реттік және аргумент функциясы (р және z) берілген. Функциямыз [-1 1] - дейінгі аралықтағы интегралда жатыр, сол үшін функция теріс, ал екінші нұсқада жиналған нүктелер санынан S кезекті нүкте функциядан SGN функциясын қолдана отырып қосалқы операторлар қысқарды.
5. 9. В бағдарламасында Бейсиктің стандартты функциясы RND(х) қолданылды, сандардың теңдей орналасу интервалы [0. 1] . [А, В] интервалына өту үшін сызықтық теңдеуді A+RND(x) +(B-A) қолданамыз. Бағдарламаның шешімі х аргументіне тәуелді емес.
5. 9. Ғ бағдарламасында RAN(i, j) стандартты функция қолданылған, аргументтер бағдарлама барысында алғашқы қадамдары нөлге тең. i, j алғашқы мәндері қайталана беруіне байланысты әртүрлі бағдарламаларды іске қосады. Сандардың қосындысы ретінде R сандар жиыны алынған.
Паскаль тілінде стандартты кездецйсоқ сандар кездеседі, сол үшін 5. 9. Р бағдарламасында RAN(i, j) функциясы Фортранның кітапханасынан алынған.
Бағдарлама барысында функция FORTRAN кезекші сөзінен аталған. SIGN функциясы да дәл солай қолданылады.
Бұндай жағдайда мынадай шартты орындауымыз керек, яғни функцияның параметрлері var типі болуы шарт.
Қорытындыға бақылау нәтижелерін 5. 9. бағдарламасына келтіреміз. 5. 9. В бағдарламасында N=200, ал S
1
=0, 763013, ал екінші нұсқада S
2
=0, 77-ге тең. 5. 9. Ғ және 5. 9. Р бағдарламасында дәл сондай параметрмен S
1
=0, 7738534, S
2
=0, 740 мәндеріне тең. Бейсик және Фортран тілдері әртүрлі шешімдерге ие болады. Ескеретін жайыт, интервалдың ұзындығы
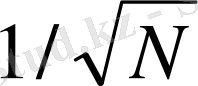 , нақты мәнді интеграл J
0
(1) = 0, 7651977-ге тең.
, нақты мәнді интеграл J
0
(1) = 0, 7651977-ге тең.
Қазіргі заман әдебиетінде «Имутациялық модельдеу» туралы нақты біріккен түйін, зейін жоқ.
Мынадай бірнеше түсініктер қалыптасқан.
1. «Имутациялық модельдеу» ұғымын математикалық ұғым ретінде классикалық мағынада;
2. Бұл термин жалпы өзгерісті талап ететін модельдерде сақталады;
3. Имутациялық модельдің математикалық модельден өзгешілігі, оның нақты сипатталуында деп ұсынады, бірақ критерилердің айтуы бойынша математикалық модель біткенде, имутациялық модель басталады.
Имутациялық модель заман талабына байланысты адамдардың араласу процестерінде қолданылады.
Имутациялы модельді классикалық математикалық модель арқылы салыстыруға болады.
Математикалық модельдің күрделі жүйедегі этаптары:
- Негізгі сұрақтар жүйенің іс-әрекеті арқылы, өздері қажетті жауапты модельдің көмегімен алу;
- Көптеген заңдылықтар бойынша басқарылған жүйенің іс-әрекеттің барысында қойылған сұрақтарға нақты жауап алу;
- Егер қажет болса мына заңдылықтарға қажетті толықтырулар енгізіп, жүйе үшін немесе оның негізгі бөліктерге формальдау модельдің кемшілігі тәжірибе барысында анықталады.
Математикалық модельді күрделі жүйеде құруда кездесетін қиындықтар:
- Егер модель ішкі элементтермен байланысқан болса, әртүрлі сызықты емес кедергілер, көп мөлшердегі параметрлі болса;
- Нақты жүйелер кездейсоқ факторлардың тоқталуына ұшырап, аналитикалық жолмен өте үлкен көлемді қиындықтарға ұшырайды;
- Мұндай әрекеттер тек баста кездеседі.
Осы кедергілер имитационадық моделл арқылы шешіледі. Олар мынадай этаптар арқылы жүзеге асырылады:
- Алғашқыдағыдай негізгі сұрақтар күрделі жүйенің жұмыс істеу әрекетіне байланысты өзімізге қажетті сұрақтарға жауап алу.
- Демократиялық жүйенің қарапайым бөліктері.
- Жүйені толығымен, сонымен қатар лның жеке бөліктеріне қатыстьы заңдар.
- Зерттеу барысында қойылатын сұрақтар аты аталған жүйенің уақытын жұмыс барысында нақты жүйеге енуі.
- формалдау нәтижесінде міндетті түрде ореноменологондық қасиеті жүйенің және оның бөлшектерінің де қажеттері беріледі.
- Модельде кездейсоқ кездесетін параметрлер жүйенің бір уақытта - жұмыс істеу \ін сақтайды. Ары қарай жаңа - ізденістер іздестіріледі.
1. 2. Имутациялық модельдеудің имутация өндірісінде
қолданылуы әдістері
Неортегаз өндірісінің жаңа этап түріндегі дамуы табиғи, экономикалық, органикалық, экологиялық факторлармен байланысты. Неортегаз өндірісі өте ұзақ уақытпен ерекшеленеді, онда технологиялық процесс (өндіру, іздеу, табу, газ және неорті деп пайда түсіру) жүзеге асырылады.
Осы факторлардың мағынасы арқылы зерттеулердің қорытындысы жаңа жерлердің пайда болуымен өнімнің өнуіне байланысты өзгеріп отырады. Осындай іс-әрекеттер кәсіпорынның оптималдық жоспарын жолспарлап қайта құруды талап етеді. Құралған жоспар бойынша шаруашылық шешімдерге қолданылатын әдістер математикалық модуль. Имитациондық модельдің көмегімен біріккен, тиянақты схеманы құра отырып, фукнционалды элементті басқару жүзеге асырылады. Негізгі өндіру процесі біршама өсті (ізденістер, өндіру, пайда, транспорт) .
Монте-Карло әдісі 1949 жылы «The Monte Carlo me that» жаңалығынан кейін пайда болды. Бұл әдістің негізгі салушы, құрастырушы американдық математиктер Дж. Неймана және С. Улома болатын. СССР-да алғаш рет Монте-Карло әдісі жайында 1955-1956 жылдары мақала жарыққа шықты. Монте-Карло әдісінің теориялық негізгі әдісі бәріне белгілі болды, оның көмегімен көптеген есептерді шешті. Алайда электронда есептеуіш машинаның (ЭЕМ) шығуы мен қарқынды дамыды. ЭЕМ-нің шығуымен бұл әдістің кең қолданылуы басталды.
«Монте-Карло» атауы Монте-карло қаласында Монако хандығының керемет үйімен байланысты.
Бұл әдістің идеясы өте қарапайым, ол мынадай іс-әрекеттен тұрады. Процесті аналитикалық аппаратпен сипаттаудың орнына, арнайы процедуралардың көмегімен сипаттауға болады. Бұл процестердің ерекшелігі - біз әр процедураны орындаған сайын статистикалық модельдерде әртүрлі, нақты, басқалардан өзгеше зерттелген процесс аламыз. Бұның бізге тигізер пайдасы не? Былайша қарап тұрсақ жай қарапайым процесс. Бірақ осы процестердің басқа әдістерден артықшылығы өте көп. Міне осындай іс-әрекеттен соң бізді қызықтыратын мінездемелер: оқиғаның болуы, математикалық болжау және дисперия және т. б.
Модельдеудің кездейсоқ пайда болған әдісі Монте-Карло әдісін біз кеңінен «бізге жұмыс істе» деп басқара ламыз.
Күрделі операцияларды орындау кезәнде, ондағы кең көлмедегі элементтерді (машина, адам, кәсіпорын) басқару өте қиынға соғады.
Міне осындай кең көлемді, ауқымды Монте-Карло әдісімен шешуге болады. Мысалы, қандайда бір мақсатты жүзеге асыруда 3 тәуелсіз ашу болды, олардың әрқайсысы ½ мақсатта болуы мүмкін. Табу керек ең болмаса біреудің дәл түсуін. Элементарлық есептеу бізге мынаны береді 1-(1/2) 3=7/8. Бұл есепті статистикалық модельдеуменде шешуге болады.
Монте-Карло әдісі - сандық әдістердің математикалық есебін модельдеудің көмегімен шешуші әдіс.
Мысал келтірейік:
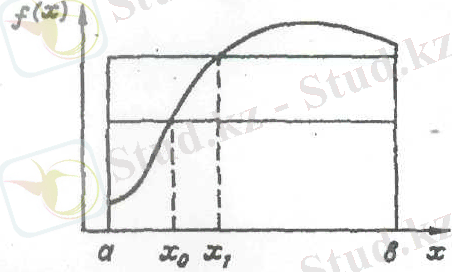
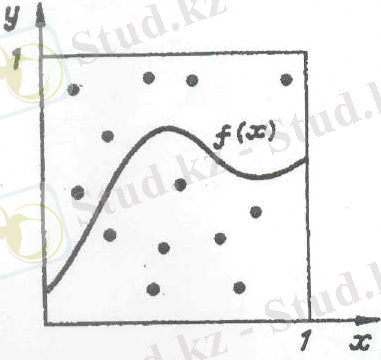
1 мысал: Мына фигураның S ауданын табу керек. Бұл фигура дөңес болуы мүмкін, көпбұрышты болуы мүмкін. Мына 1-суретте көрсетілгендей, біріккен квадраттың ішінде орналасқан. Квадраттың ішінен N нүктесін аламыз. Ғ нүктесі арқылы S-ті табамыз, онда S-міз Ғ/N-ге қатынасындай, неғұрлым N үлкен болса, соғұрлым нақты болады.
Монте-Карло әдісінің 2 ерекшелігі:
- қарапайым алгоритм;
- есептің барысы D/N2пропорционал;
мұнда D - тұрақты, N - кез-келген сан.
Есептің барысында нақты шешім алу үшін 10 рет, ал N 100 үлкейтуіміз керек. Бірақта нақты жауапты алу өте қиын. Сол себепті Монте-карло әдісінің тиімділігі оның нақты жауабы қажеттілігінде (5-10) Монте-Карло әдісін қолдану өте қарапайым. Ол үшін мынадай іс-әрекеттер орындалады.
- График немесе таблица құруымыз керек.
- Кез-кеоген 0 1 дейінгі сандарды алу.
- Горизанталь бойынша осьтер қисық сызық болуы керек.
- Осы нүктелер арқылы абсцисса осіне перпендикуляр жүргіземіз.
- Берілгенді Х деп белгіле.
- Іс-әрекетті 2-5 қадамнан соң қайтала.
Бұны өте қарапайым мысалмен түсіндіруге болады: 1 минут ішінде телефон станциясына қанша телефон қоңырау соғылды:
5 уақыт аралығына тәжірибе жүргізіп көрейік. Кумулятивтік болжау бойынша график құрастырамыз. Генератордың көмегімен кез-келген сандардан 5 санды аламыз. Оларды интервал уақыты ретінде аламыз.
ІІ бөлім Сызықты алгебралық теңдеулер жүйесін
Монте-Карло әдісімен шешу.
2. 1. Монте-Карло әдісінің имутациялық модельдеуге
тигізер пайдасы
Тағыда осы секілді бірнеше сандарды алып, қолданылған сандар расында да ретпен орналасқанын байқауға болады.
Енді мысалға келетін болсақ, есептеу үшін біз әртүрлі нүктелерді өз қалауымыз бойынша квадраттың бойынан алдық. Бұны енді қалай физикалық етуге болады?
Мынадай тәжірибені алайы: (1 сурет көлемін үлкейтейік) .
S фигурасымен және квадрат қабырғаға иілуі. Атқыш қабырғадан бірнеше қадам алшақ тұрады, ал N рет атады, квадраттың ортасына тигізгенше.
Әрине бьарлық октар дәл квадраттың ортасына түспейді. Осы нүктелер арқылы ауданын S анықтауға болады ма?
Қатты жылдамдықпен атылған оқтың нәтижесі жақсы емес, себебі барлық атылған оқтар S-ң маңайында жатады. Сол үшін біздің ауданның көлемін табу әдісіміз қай кезде: «әділ» болады, егер біздің нүктелеріміз квадраттың бойымен өлшемді түрде орналасқан кезде әділ болады.
Монте-Карло әдісі мынадай 3 негзгі зертеулерде қолданылады:
- Күрделі модельдеуде, комплекстік операцияларда;
- Қарапайым аналитикалық әдістерде;
- Аналитикалық формулалар барысында.
Мысал: Геологиялық артықшылықты бағалауды анықтау.
Геологиялық байлықты анықтамастан бұрын оның типін анықтап алуымыз керек.
Бағаны анықтау үшін неорт немесе газдың құрамын біле отырып, оның құрылысын анықтау қажет.
Олар: көлемі (RV) пористости (Ғ), суқұбыры (SW), эфоректік жылдамдық (NP) .
Бұл этапты геологтар геологиялық артықшылықты қолдануға кететін параметрлерді анықтап алу қажет. Әрбір параметрдің өзіне тән интервалы болуы шарт.
График түрінде:
1, 2, 3, 4, 5 суреттерде көрсетілген график болжау графигі болып табылады. Қисық сызық параметрлердің тең немесе үлкендігін анықтайды. Қисық құрастырылған гистограмма бағананы сипаттайды. Гистограммалар геологтар мен геофизиктердің іздену бағасына анықтай отырып, мынадай мәліметтер бере алады:
- біздің ойымызша, пород көлемі 0-ден 390 мың футқа дейінгі интервалда жатады 10%.
- біздіңбағалауымызша, пород көлемі 380-нен 550 куб футқа дейін, ол 15% құрайды.
Геологтардың бағалауы бойныша қисық болжау пайда болады. Геологиялық қорлар мынадай формулалардың көмегімен анықталады:
RVxFx(1-SW) xNPx; - мұндағы Ғv - неортінің коэффициенті.
Орта есеппен алғанда геологиялық қорларды анықтағандығы нәтиже мынадай:
- орта көлемді парод 1, 35 млн. Акрофут құрайды, (1 акрофут=7760 баррелей немесе 1230м3) .
- Орта пористость - 17%.
- Орта водонасыщенносты - 20%.
- Орта эффектік жылдамдық - 7, 5%.
- өткізу коэффициенті - 1, 02.
Енді осы көрсеткіштерді формулаға қойып, есептейік:
(1. 5x10) x(1 7%) x(1-20%) x(75%) x(98%) = 135x0. 17x0. 8x0. 75x0. 98) = 134946 акрофут немесе 134946х7760=1047413760 жуық шамамен 1, 047 млрд баррелей неорті (165 млн. М 3 , 141 млн т) .
Өте кең тараған әдіс - Монте-Карло әдісі. Ең алдымен әрбір параметр үшін метограмма құруымыз қажет.
Әрбір қисық үшін 0-ден 100% дейінгі нүктені таңдау қажет. Одан соң геологиялық қорларды мына параметрлер бойынша анықтауға болады.
Мысалы: 1, 2, 3, 4 суретерді алайық.
- 50% үшін - 25% парод көлемі 69 акрофут.
- 20% үшін - 35% иеленеміз, поритост 21% құрайды.
- 25% үшін - 25%, суқұрамы - 33%-ға тең.
- 80% - 32%-ды көрсетсе, эффектінің жылдамдық - 74%.
- Көрсеткіш коэффициенті - 1, 02.
Осы мәндерді қолдана отырып, геологиялық қорды анықтаймыз:
(0, 69х10) х(21%) х(1-33%) х(74%) =521 млн баррелей неорт (82 млн м 3 , 70 млн т) . Бұл есептің шешімі өте төмен, орта мәндегі параметрлерге қарағанда. Бізге нақтылықты білу қажет. Ол үшін геологиялық қор 521 млн баррелей неортті құрайды, толықтылықты анықтайтын болсақ.
0, 25х0, 35х0, 20х0, 35х1, 0=0, 006125. Бұл процедура бірнеше рет қайталанады. ЭЕМ үшін қолданылатын прогшраммалар өте тиімді. Ол бізге нақты, әрі дәл геологиялық қорларды анықтауға мүмкіндік береді. Программаның қорытындысы бойынша геологиялық қор неортінің: 84658 акрофут немесе 88, 5 млн тоннаны құрайды.
Келесі этапта графикті қолдана отырып, оның көмегімен проектінің құрылысын, табысты анықтауға болады. Бұл есептер ақшалай эксплуатацияны анықтауға себептігін тигізеді. Графиктен алынған мәндерге. Осы мәндер арқылы эжкономикалық көрсеткіштерге анализ жасауға болады. Уақыт өте коэффициенттің мәндері формула бойынша анықталады.
Коэффициент көрсеткіші = скважин давш неорт көлемі/пробур көлемі.
Бірнеше жыл өте график тәсілі әлдеқайда жақсы жетістікке жетті. Мысалы, келісімді аудан үшін график коэффициенті 10 жыл бұрын эксплуатация кезінде де жақсы көрсеткіш көрсеткен.
Белгілі мәндер арқылы сызықтар, одан соң олардың центрі арқылы қисық сызықтар өтеді.
Осы сызықтардың соңғы нүктелері максималдық жетістік шегін, ал орталық қисықө алдағы жетер жетістіктердің шарықтау шегін көрсетеді. Мәндер болжамы негізгі субъектілер арқылы анықталады.
Қордың көлемін аналогиялық шекпен анықталады. Көрсеткіш коэффициентінің көмегімен қордың белгілі шегін, бағдарлама барысында қажетті мөлшерін білуге болады.
2. 2. Сызықты алгебралық теңдеулер жүйесін пайдаланып, геологиялық
артықшылықтарды бағалау.
Монте-карло әдісімен САТЖ-ін шешу алгоритмі төмендегідей ретпен іске асырылады. Берілген теңдеулер жүйесін
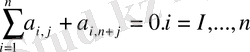
түрде жазамыз.
Бұл жүйені итерациялық әдісті пайдаланатын нормаль түрге келтіреміз. Ол үшін, кейбір і мәнінде
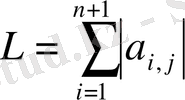
болсын.
Егер жүйенің і-ші теңдеуі а i, j >0 болса, оның әрбір мүшесін - L, ал а i, j <0 болса, онда +L санына бөліп,
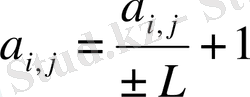 және
және
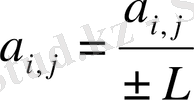
белгілеуін енгіземіз.
Әрі қарай жүйені нормаль түрге келтіреміз:
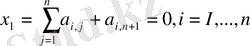
Нормаль теңдеулер жүйесі үшін
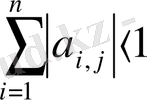
теңсіздігі (интернационалдық процестің жинақтылығының жеткілікті шарты) орындалсын деп жориық. Енді жүйенің і-ші теңеуіне [0. 1] кесіндісін S і нүктелерімен n+1 кесіндіге бөлуді сәйкестейміз, мұндағы S і координаталары:
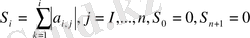
Бастапқыда [0. 1] аралығының і-ші кесіндінің кейбір S і нүктесі осы [S n , S i ], [S i , S j ], …, [S n , S n+1 ] аралықтарды кездейсоқ «аралауын» қарастырайық. [0. 1] аралығына тиісті кейбір С кездейсоқ санын аламыз. Егер ол қарастыратын і-ші аралық үшін
S j-1 ≤ C ≤ S j , j = 1, 2, …, n
теңсіздігі қанағаттандырсақ оны і-ші бөліктің S
і
нүктесінен j-ші бөліктің S
j
нүктесіне көше алады деп есептейміз. Әрі қарай аралық үшін тағы да кездейсоқ. С санын аламыз. Егер
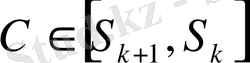 болса, онда нүкте j-да бөліктің S
j
нүктесінен k-ші бөліктің S
k
нүктесіне көше алады. Осылай, ақыры С нүктесі [S
n
, S
n+1
] кесіндісіне тап болғанда, ол S
n+1
нүктесіне көшеді де, «адасу» аяқталады. Нүктенің S
i
, S
j
, …, S
m
, S
n
траекториясына
болса, онда нүкте j-да бөліктің S
j
нүктесінен k-ші бөліктің S
k
нүктесіне көше алады. Осылай, ақыры С нүктесі [S
n
, S
n+1
] кесіндісіне тап болғанда, ол S
n+1
нүктесіне көшеді де, «адасу» аяқталады. Нүктенің S
i
, S
j
, …, S
m
, S
n
траекториясына
Y i = V j * V ik . . . W m
қатынасы арқылы анықталатын кездейсоқ у і көлемді сәйкес қоямыз, мұндағы
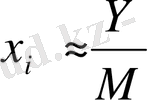
мұндағы
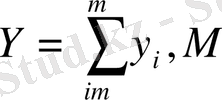 -нүктенің кездейсоқ «адасу» саны. Кездейсоқ процестер мен құбылыстарды модельдейтін (математикалық тілде жазатын) алгоритмді
- ықтималдық алгоритмдер
деп атайды. Ал кездейсоқ шамаларды пайдаланып есептер шығаруды Монте-Карло әдісі деп атайды. Бұл әдістің негізі - кездейсоқ сынау, бірнеше рет қайталау. Монте-Карло әдісінің ерекшелігі кездейсоқ сандарды пайдалану. Егер берілген кесіндіні ұзындықтары тең, саны шектеулі кейбір аралықтарға бөліп, RND функциясының мәнін бірнеше рет есептесек, онда әрбір [S
i
, S
j+1
] аралықта шамамен саны бірдей кездейсоқ сандар табылады. Міне, осы идеяны САТЖ шешуге пайдалануға болады екен. Бұл әдістің тағы да бір ерекшелігі: теңдеулер жүйесінің барлық белгісіздер мәнін таппай-ақ, олардың тек біреуін ғана табуға болады. Монте-Карло әдісінің дәлдігі аса жоғары емес. Монте-Карло әдісінің ықтималдық алгоритмі келтірілген.
-нүктенің кездейсоқ «адасу» саны. Кездейсоқ процестер мен құбылыстарды модельдейтін (математикалық тілде жазатын) алгоритмді
- ықтималдық алгоритмдер
деп атайды. Ал кездейсоқ шамаларды пайдаланып есептер шығаруды Монте-Карло әдісі деп атайды. Бұл әдістің негізі - кездейсоқ сынау, бірнеше рет қайталау. Монте-Карло әдісінің ерекшелігі кездейсоқ сандарды пайдалану. Егер берілген кесіндіні ұзындықтары тең, саны шектеулі кейбір аралықтарға бөліп, RND функциясының мәнін бірнеше рет есептесек, онда әрбір [S
i
, S
j+1
] аралықта шамамен саны бірдей кездейсоқ сандар табылады. Міне, осы идеяны САТЖ шешуге пайдалануға болады екен. Бұл әдістің тағы да бір ерекшелігі: теңдеулер жүйесінің барлық белгісіздер мәнін таппай-ақ, олардың тек біреуін ғана табуға болады. Монте-Карло әдісінің дәлдігі аса жоғары емес. Монте-Карло әдісінің ықтималдық алгоритмі келтірілген.
Теңдеулер жүйесінің
5х 1 - х 1 + х 4 - 7 = 0
- x 1 + 8x 2 + 2x 1 - 3x 4 - 9 =0
2x 2 + 7x 3 - x 4 - 21 = 0
x 1 + 3x 3 - x 3 + 6x 4 - 28 = 0
шешімін Монте-Карло әдісімен табыңдар.
Шешуі. Есептеуді Монте-Карло әдісінің алгоритмінің блок-схемасы бойынша жүргіземіз. і=I болса формуладан:
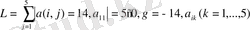
формула бойынша:
a 11 = -5/14 = -0. 3572; a 12 =0. 0714; a 13 =0; a 14 =0. 0714; a 15 =0. 7;
Келесі қадамда a 11 = a 11 + 1 деп есептейміз де формуладан
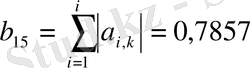
формула бойынша w(1) =a 15 /(1-b 15 ) =2. .
Міне, осылай і=2 мәнінде:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz