Мектеп математикасында мазмұнды есептерді шешуге оқыту әдістемесі


КІРІСПЕ
Мазмұнды есептердің математикадағы орны ерекше екені белгілі. Мазмұнды есептер арқылы оқушылардың ойлау қабілетін кеңейтуге, практикалық жағдайлармен таныстыруға, сонымен қатар тәрбиелік жағына көңіл бөлуге болады. Оқу процесінде қарастырылған математикалық білімдерді меңгеру, оларды іс жүзінде қолдана білуге дағдыландыру үшін есеп шығаруға үйрету мақсат десек, мазмұнды есептерді шығаруға үйрету осы мақсатқа жетуге әсерін тигізетін әдіс болып табылады.
Оқушылардың есеп шығару барысында іскерлігі мен дағдыларын қалыптастырудың қиындығы олардың есеп шығару барысындағы іс-әрекеттеріне, ойлау қабілеттеріне жүйелі де тиянақты талдау жасалмауына байланысты екенін мектеп тәжірибесі көрсетіп отыр.
Әрине, есептердің негізгі мақсаты алған білімді іс жүзінде әр түрлі жағдайларда қолдануға үйрету және бұл білікті әрі қарай дамыту болып табылатыны белгілі. Мазмұнды есептерді шығару - математикалық білімді өмірмен тығыз байланыстыруға, сондай-ақ оқушылардың өмірден алған тәжірибелерін математиканы оқып білуге кеңінен пайдалануға және мектепте алған білімдерін еңбекпен байланысты іс-әрекеттерінде қолдана білуге көмектеседі.
Дипломдық жұмыстың зерттеу объектісі - мазмұнды есептер, мектепте мазмұнды есептерді шешуге оқыту процесі.
Дипломдық жұмыс кіріспеден, үш параграфтан, қорытындыдан, қосымшадан және әдебиеттер тізімінен тұрады.
Бірінші параграфта мазмұнды есептің анықтамасы беріледі, мазмұнды есептердің шығу тегі, есепті шешу мақсаттарының қандай болғандығы, олардың уақыт өте келе қалай өзгергендігі қарастырылады.
Дипломдық жұмыстың екінші параграфында Қазақстан Республикасының жалпы білім беретін мектептерінде қолданылып жүрген оқулықтар негізінде мазмұнды есептердің классификациясы келтірілген.
Дипломдық жұмыстың үшінші параграфы қазіргі мектеп курсындағы есептерді шешуге оқыту әдістемесіне арналған. Оқу процесіндегі мазмұнды есептердің мақсаттары мен атқаратын дидактикалық функциялары, мазмұнды есептерді шешу процесінің құрылымы қарастырылған. Кестелік модельге жан-жақты жеті сұрақ түріндегі толықтырма ұсынылған. Қозғалысқа арналған есептерді шығару кезінде есептегі жағдайды модельдеуге есептер қарастырылды. Мазмұнды есептерді құру бойынша ұсыныстар берілді, себебі оқушылардың есепті өздігінен құруы - оларды есепті шешуге үйретудің тиімді құралы болып табылады.
Қосымшада ежелгі мазмұнды есептер келтірілген.
Жұмыстың маңыздылығы мынада: оқушыларды мазмұнды есептерді шешуге үйретуді бірден есепті шешуден емес, есептердің теориясын оқытудан бастау және оларды есепті құруға үйретуден бастау ұсынылады. Оқушыларды әлдебір әдіске емес, жалпы әдіс - модельдеуге үйрету.
§3. Оқушыларды мазмұнды есептерді шешуге оқыту методикасы
3. 1. Мазмұнды есептерді шешудің жалпы мақсаттары
Есептердің математиканы оқытуда алатын орны және атқаратын қызметі әрқашан оқытудың жалпы мақсаттары арқылы анықталады. Бұл функциялардың ішіндегі ең маңыздысы - ол кез-келген есепті шешу барысында оқушылардың жалпы қабілеттіліктерін қалыптастыру және дамыту функциясы.
Бұл - біз есепті шешу кезінде есептің шешімін тауып қана қоймай, оны шешу әдісін де меңгеруіміз керек дегенді білдіреді.
Есепті шеше білу білім мен машықтың синтезі болуы тиіс.
Қазіргі уақытта есепті шешу кезінде басты назар негізінен есептің жауабын табуға аударылады. Есепті талдау, есептің моделін құру, оны шешу тәсілін іздестіру ерекше өзіндік жаттығу болып табылмайды, тек элемент ретінде есепті шешудің жалпы процесіне кіреді.
Оқушылар есепке талдау жасауды немесе оны шешудің теориялық негізін іздестіруді үйренуі үшін бұл амалдар оқушылар үшін өзіндік жаттығу болуы тиіс. Математика курсында төмендегідей жаттығулар саны жеткілікті болуы тиіс: “Есеп берілген (текст келтіріледі) . Осы есепке талдау жаса”. Бұл жерде есептің шешімін анықтамаймыз. Немесе: “Есеп берілген (оның тексті) . Осы есептің барлық мүмкін (немесе белгілі бір) модельдерін құр” және т. б. Мұндай тапсырмалар оқушыларға әртүрлі есептерді түсініп отырып шығаруына мүмкіндік береді.
Қазір біздің және оқушылардың назары есептің шешімін тезірек табуға бағытталған. Талдауға, орындалған шешімнен қандай қорытынды жасауға болатынын анықтауға уақыт та, күш-қуат та қалмайды, ал олар ең маңызды болып табылады. Бұлардың барлығы назардан тыс қалып отыр, себебі ол басқа бір техникалық қиындықпен (шешімді табу) көлегейленіп қалған.
Егер оқушылар есептің шешімін белгілі бір жоспар бойынша жүргізе білген болса, онда бұл қиындықтар екінші орында, ал бірінші орында есепті шешудің оқу-танымдық мақсаты болар еді.
Мазмұнды есептерді шешудің негізгі мақсаттары :
- оқушылардың кез-келген есепті шешудегі жалпы көзқарасын, жалпы қабілеттіліктерін қалыптастыру;
- қарастырылатын математикалық және жалпы ғылымдық ұғымдарды танып, терең меңгеру;
- модель және модельдеу, математикалық модельдеу ұғымдарын меңгеру.
Есепті шешу процесінде бұл мақсаттарды жүзеге асыру ісін оқушылардың жалпы психикалық және ақыл-ойының дамуына тиімді әсер ететіндей жүргізу қажет.
21
3. 2. Мазмұнды есептердің оқыту процесінде атқаратын дидактикалық функциялары
1. Оқушылардың алдына қандай да бір проблемалы есепті қою - оларды оқу-танымдық іс-әрекетке қызығушылығын қалыптастырудың маңызды құралы болып табылады. Мұндай есептер оқыту процесінде кіріспе-мотивациялы функция атқарады.
2. Математиканы оқу процесінде оқушылар әртүрлі математикалық ұғымдармен танысады. Олар осы ұғымдардың мән-мағынасын терең түсінуі үшін бұл ұғымдарды бірнеше мысал арқылы көрсетіп, нақтылау қажет. Бұл жерде қарастырылып отырған ұғымдардың ерекшеліктерін көрсететін әртүрлі мазмұнды есептерді қолданған дұрыс.
3. Математикалық заңдылықтарды қолдану және іске асыру функциясы. Оқушылар мектептік математика курсында оқытылатын заңдылықтарды терең меңгеруі үшін, олардың практикалық маңыздылығын түсінуі үшін мазмұнды есептер жүйесін пайдалануға болады. Бұл есептерді шеше отырып оқушылар сол математикалық заңдылықтардың практикалық маңыздылығына көз жеткізеді.
4. Математикалық білігі мен дағдыларын қалыптастыру функциясы. Мектептік математика курсында оқушылар бірнеше арнайы математикалық: есептеу (ауызша және жазбаша), қарапайым шамаларды өлшеу, оларды өзара салыстыру, геометриялық салуларды орындау, т. б. Білік пен дағдыларды игеріп шығуы тиіс.
5. Жалпыоқыту біліктерін қалыптастыру функциясы. Математиканы оқыту процесінде арнайы математикалық біліктер мен дағдыны қалыптастырудан басқа, оқу, жазу, анықтамалық және оқу материалдарын дұрыс пайдалану, жазбаша тапсырмаларды тиянақты және дұрыс орындау, өзінің оқу процесіндегі жұмысын басқаруды және өзін-өзі бағалауды іске асыру, т. б. көптеген жалпыоқыту білігі мен дағдыларын қалыптастырып, дамытып және бекітіп отыру қажет.
6. Оқушының мінез-құлқын және ерік-жігерін тәрбиелеу функциясы. Мазмұнды есептерді шешу, әсіресе күрделі есептерді шешу оқушылардан жүйелі және дәлелді талдауды, есепті шешу кезінде пайда болып отыратын қиындықтарды жеңуде қажетті жинақылықты, сәтсіздіктен қорықпауды, сәтсіздіктер мен жетістіктерден өзіне қажетті пайдалы қорытынды шығаруды, т. б. талап етеді. Бұлардың барлығы оқушының мазмұнды есепті жеке өзі шығарғанда, оған есепті таңдауда да, есепті шешуге бөлінген уақытта да еркіндік берілген жағдайда тәрбиеленеді және дамытылады. Шешілген есептер санына көңіл бөлмеу керек, керісінше есепті шешуге жеткілікті уақыт беріп, үйде аяқтауға рұқсат беру керек.
7. Шығармашылық ойлауды дамыту функциясы. Математикада “зеректік пен тапқырлыққа” арналған көптеген есептер құрастырылған, оларды шешу үшін қандай да бір ерекше тәсілдер қажет. Бұл есептерді шешу оқушылардың шығармашылық интуициясын және ынта-ықыласын дамытуға септігін тигізеді. Оқушыларға мұндай есептерді жеке үй тапсырма ретінде ұзақ уақытқа беруге
22
болады. Математикалық олимпиадаларды және басқа да жарыс түрлерін өткізу пайдалы болады.
3. 3. Мазмұнды есептерді шешу процесінің құрылымы
Мазмұнды есепті шешу бірмезеттік әрекет емес, ол - оқушылардың күрделі және жоспарлы жұмысы болып табылады. Есепті шешу процесі осы есепті шешудегі мақсаттарды жүзеге асыруға пайдалы болатындай етіп жүргізілуі тиіс.
1. Есепті талдау екі бағытта жүргізілуі мүмкін: заттық-мазмұнды талдау және логикалық талдау. Заттық-мазмұнды талдау - бұл моделі берілген есеп болып табылатын өмірден алынған жағдайды қайта жаңғырту. Әдетте мұндай талдау ауызша жүргізіледі, және осы талдауды негізге ала отырып есепті шешетін адам оның сюжетін өз ойында бейнелейді. Бұл бейне анық болған сайын ол есепті шешетін адамға келесі талдауды жүргізуге, есепті шешу әдісін іздестіруге көп көмектеседі. Логикалық талдау - бұл есептің текстінде берілген шамаларды, олардың мәндерін және олардың арасындағы арақатынастарды анықтау үшін, осылайша есептің текстін элементар шарттар мен талаптарға жіктеу үшін жүргізілетін талдау. Осылайша есептің құрылымы анықталады.
Есепке логикалық талдау жүргізу нәтижесінде:
- қандай шамалар есептің мазмұнын құрайтын құбылыстар, процестер мен оқиғалардың сандық жағын сипаттайтыны;
- есепте әр шаманың айқын немесе айқын емес түрде неше және қанша мәні берілгендігі;
- шаманың әрбір мәнінің сипаты: бұл мән белгілі ме немесе белгісіз бе, ал егер белгісіз болса, онда қандай - ізделінді, аралық немесе анықталмаған;
- шамалардың бұл мәндері өзара қандай арақатынаспен байланысты екендігі;
- әр арақатынастағы басты мән, осы мәннің сипатын көрсететін белгілер;
- осы арақатынастардың әрқайсының сипаты(шешілетін немесе шешуге болатын) ;
- бұл арақатынастардың байланысы анықталады.
2. Есептің моделін құру мақсаттары: есепті талдау нәтижелерін бекіту; есепке әртүрлі тұрғыдан қарау; есептің гегізгі математикалық моделін даярлық кезеңі.
Егер берілген есеп қарапайым болса, онда оның моделін құрмай-ақ қоюға болады. Егер есеп күрделі болса, онда оның моделін құру қажет, себебі бұл модель есепті шешу тәсілін іздестіруде көмектеседі.
Есептің моделі әртүрлі болуы мүмкін: схемалық, кестелік, құрылымдық, графикалық және т. б. Есептің моделін таңдау оның сипатына ғана емес, есепті шешетін адамның мінезіне ерекшеліктеріне, оның білігі мен дағдыларына байланысты болады.
Есептің моделін құру - оқушының есептің әртүрлі моделін құру білігі мен дағдысын қалыптастыру үшін берілетін маңызды жеке жаттығу болуы мүмкін.
23
3. Есепті шешу тәсілін іздестіру. Есепті көптеген әдістермен шешуге болады. Есепті шешу тәсілін таңдау алдымен есепті шешетін адамға байланысты: оның біліміне, оған қандай тәсіл үйреншікті екеніне. Сонымен қатар есептің сипатына және ерекшеліктеріне байланысты. Берілген есепті шешуге қандай да бір тәсілді таңдау туралы мәселені оқушылар бірігіп талдаса, бұл да пайдалы болады.
4. Есептің шешуші математикалық моделін құру. Мазмұнды есепті шешу тәсілін таңдағаннан кейін, оған сәйкес шешуші математикалық модельді құру керек. Егер арифметикалық әдісті таңдаса, онда модель есептеу формуласы немесе арифметикалық амалдар тізбегі түрінде құрылады; егер алгебралық әдіс таңдалса, онда теңдеулер мен теңдеулер жүйесі, теңсіздіктер мен аралас жүйе түріндегі модель құрылады; т. с. с.
5. Есептің шешімін тексеру табылған шешімнің есептегі барлық шарттарды қанағаттандыратынын анықтаудан тұрады. Шешімді әртүрлі тәсілдермен тексеруге болады. Есепті тура және жанама тексеруге болады, және бұлардың әрқайсының өзі толық немесе жартылай түрде болуы мүмкін.
Есептің шешімін толық тура тексеру кезінде біз есептің барлық шарты ізделіндінің табылған мәндерінде орындалатынына көз жеткіземіз. Ал толық емес тексеру кезінде тек кейбір шарттарының ғана орындалатынын тексереміз.
Есептің шешімін жанама түрде тексеру берілген есепке кері есеп құрып, оны шешу арқылы жүргізіледі. Кері есеп ізделіндіні берілгендердің біреуімен орнын ауыстыру жолымен құрылады. Егер кері есепті шешу нәтижесінде таңдаулы берілген мәнмен сәйкес келетін мән табылса, онда тексеру “үйлеседі”. Әрбір мазмұнды есеп үшін бірнеше кері есеп құруға болады, шешімді тексеру үшін оңай шешілетін есеп құрады.
6. Есептің жауабын тұжырымдау. Әдетте есептің жауабы есептің талабына немесе сұраққа жауап формасында тұжырымдалады. Егер осы жауап белгілі бір шарттар орындалғанда ғана дұрыс болса, бұл шарттар жауапта көрсетіледі. Егер бірнеше шешім болса, олардың барлығы жауапқа жазылады.
7. Оқу - танымдық этап. Оқушылар мазмұнды есепті оның жауабын табу үшін емес, есепті шешу кезінде нақты білім алып, өздерінің қабілеттері мен біліктерін дамыту үшін шешуі керек. Сондықтан жүргізілген шешімді талқылау, талдау және зерттеудің маңызы есепті шешу маңызынан кем емес.
Жүргізілген есепті шешу процесінің кемшіліктерін анықтау, есепті шешу барысында қолданылған амалдар мен тәсілдерді оқушылардың есіне сақтату, осы амалдар мен тәсілдерді қолдану мүмкіндігінің шарттарын анықтау - бұлардың барлығы есепті шешу процесінің үлкен бір білім беру және тәрбиелеу құралына айналуына себеп болады.
3. 4. Есепті шешу процесінде кестелік модельді пайдалану
Есептің берілгендерінен, ізделінділерден, шарттар мен талаптардан тұратын арақатынастарды кестелік формада жазу - есептің шешімін
24
алгебралық әдіспен іздестірудің ең тиімді көрнекі моделі болып табылады. Бұл формаға әртүрлі есептерді шешуде қолданылатын жан-жақты 7 сұрақты қосамыз.
Сұрақтар (жақша ішінде түсініктеме берілген) :
- Есепте қандай процесс туралы айтылған? Бұл процесс қандай шамалар арқылы сипатталады? (Олардың саны құрылатын кестедегі қатарлар санын анықтайды. )
- Есепте неше процесс туралы айтылған? (Олардың саны кестедегі бағандар санына тең. )
- Қандай шама белгілі және нені табу керек? (Кестеге есептің берілгендері және сұрақ белгісі жазылады. )
- Шамалар қалай байланысқан? (Формулаларды жазып алып, кестеде шамалардың байланысы анықталады. )
- Қай шаманы мысалы, әрпімен белгілеу қолайлы болады? (арқылы сұрап тұрған шаманы немесе басқа бір шаманы белгілеген дұрыс па екендігі талданады. Сосын басқа белгісіз шамалардыарқылы өрнектейміз, олардың әрқайсына кестедегі бос тор көз сәйкес келеді. )
- Теңдеу құру үшін қай шартты пайдалану керек? (Ол шарт - белгісіздердіарқылы өрнектеуде қолданылмаған шарт. Оқушы теңдеу құруға қажет шартты және теңдеудің өзін жазады. )
- Құрылған теңдеуді шешу оңай ма? (Оқушы бұл сұраққа жауап бере отырып, “әріптік белгілеуді кестенің басқа қатарына жазу керек емес пе?” және “теңдеу құру үшін шамалар арасындағы басқа байланысты қолдану керек емес пе?” деп ойлануы тиіс. )
Мысалдар
3. 1. Есеп. Жоспар бойынша трактористер бригадасы егінді 14 күнде шауып бітіруі керек болатын. Бригада күніне жоспарда белгіленгеннен 5 га артық шауып отырды, сондықтан олар егін шабу жұмысын 12 күнде аяқтады. Неше гектар жер шабылды? Егіннің ауданын табыңдар.
Оқушы есепті оқып, сұрақтарға мына түрде жауап бере бастайды (шамамен) :
- Жұмыс процесі туралы айтылады. Ол үш шамамен сипатталады: барлық жұмыс (A) - бұл гектармен өлшенетін егіннің ауданы; бірлік уақыт мезетіндегі жұмыс, яғни еңбек өнімділігі (N) және уақыт (t) - жұмысты істеуге кеткен күндер саны. Демек, кестеде үш қатар болуы керек
(A, N, t) .
- Есепте жұмыстың екі процесі туралы айтылған: жоспар бойынша және іс жүзінде орындалған жүмыс. Демек, кестеде екі баған болады.
- Енді кесте құрып, оны берілген арақатынастармен толтыру керек.
25
1-кесте
А ж -? А ор. -?
бірдей
4) A= Nt формуласы бағандардағы шамалардың байланысын анықтайды. Қатарлардағы шамалардың байланысы таблицада көрсетілген: І байланыс,
ІІ байланыс.
5) Сұрақ: “Қай шаманы әріппен белгілеген қолайлы болады?”. Оқушы
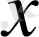 арқылы есептің сұрағындағы шаманы белгілесін, яғни
арқылы есептің сұрағындағы шаманы белгілесін, яғни
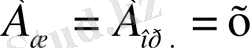 .
.
6) Сонда қолданылмаған ІІ байланыс:
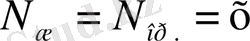 Equation. 3 теңдігі теңдеу құруда пайдаланылады, яғни
Equation. 3 теңдігі теңдеу құруда пайдаланылады, яғни
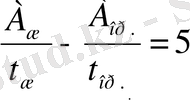
. (1)
7) Бұл теңдеуде бөлшек бар, олардан құтылуға тырысу керек. Сондықтан оқушы ”
 -ті таблицаның екінші қатарына енгізу қолайлы болмас па екен” деп ойлануы тиіс. Сонда І байланыс:
-ті таблицаның екінші қатарына енгізу қолайлы болмас па екен” деп ойлануы тиіс. Сонда І байланыс:
 теңдігі теңдеу құруға шарт болады.
теңдігі теңдеу құруға шарт болады.
Егер
 Equation. 3 болса, онда
Equation. 3 болса, онда
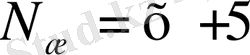 Equation. 3 болады. Сонда
Equation. 3 болады. Сонда
 шартына байланысты
шартына байланысты
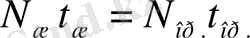 Equation. 3
Equation. 3
 Equation. 3 болады.
Equation. 3 болады.
 Equation. 3 теңдеуін алдық. (2)
Equation. 3 теңдеуін алдық. (2)
(2) -теңдеу (1) -теңдеуге қарағанда қарапайым, демек, аудан
(2) -теңдеуді шешкеннен кейін ғана табылатынына қарамай есепті шешудің екінші тәсілін пайдалану керек.
Оқушы есептің шешімін дәптеріне жазады.
Шешуі.
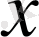 (га/күн) - бригаданың жоспарда көрсетілген өнімділігі, ал
(га/күн) - бригаданың жоспарда көрсетілген өнімділігі, ал
 (га/күн) - бригаданың іс жүзіндегі өнімділігі болсын. Жоспардағы жұмыс -
(га/күн) - бригаданың іс жүзіндегі өнімділігі болсын. Жоспардағы жұмыс -
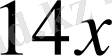 (га), ал іс жүзінде орындалған жұмыс -
(га), ал іс жүзінде орындалған жұмыс -
 (га) құрайды. Шарт бойынша егіннің ауданы:
(га) құрайды. Шарт бойынша егіннің ауданы:
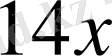 (га) және
(га) және
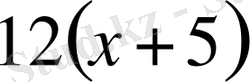 (га), екі жағдайда да бірдей. Сондықтан
(га), екі жағдайда да бірдей. Сондықтан
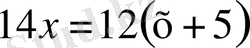 Equation. 3 теңдеуін құруға болады.
Equation. 3 теңдеуін құруға болады.
 Equation. 3 теңдеуі, бұдан
Equation. 3 теңдеуі, бұдан
2
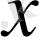 =60,
=60,
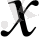 =30.
=30.
Жоспар бойынша өнімділік 30га/күн болады. Сонда егіннің ауданы 14·30=420(га) болады.
Жауабы: егіннің ауданы 420 га тең.
Әрине, барлық талдауды толығымен жүргізу қажет те емес, оқушы
бірден (1) -теңдеуді шығара алады, бірақ ол есепті шешудің қарапайым жолын
26
іздестіруді үйренуі керек.
3. 2. Есеп. Екі жолаушы бір уақытта А аулынан шығып, В аулына әр түрлі бағытта кетті. Біріншісі - 30км, екіншісі - 20км жол жүруі керек. Бірінші жолаушының қозғалыс жылдамдығы екінші жолаушының жылдамдығынан 3км/сағ. артық еді. Бірақ екінші жолаушы В аулына бірінші жолаушыдан 20мин бұрын жетті. Әр жолаушы жолда қанша уақыт болды?
“Қозғалысқа” арналған есеп. Жеті сұраққа жауап береміз.
- Есепте қандай процесс туралы айтылған? Бұл процесс қандай шамалар арқылы сипатталған?
Келесі үш шамамен сипатталған қозғалыс процесі туралы айтылған: s - жол(км), v - жылдамдық(км/сағ), t - уақыт(сағ) (минутты сағатқа айналдыру керек) . Демек, кестеде үш қатар болады.
- Есепте неше процесс?
Есепте қозғалыстың екі процесі туралы айтылған: 1-жолушының қозғалысы және 2-жолаушының қозғалысы туралы. Демек, “Шамалар” деген бағаннан басқа екі баған керек.
- Не белгілі және нені табу керек?
Әр жолаушының жолы және жылдамдықтарының айырымы белгілі. Әр жолаушының қозғалыс уақыты белгісіз. (Бұлардың барлығын 2-кестеге жазамыз. )
2-кесте

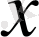
3км/сағ. артық
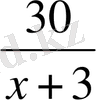 ? ?
? ?
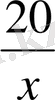
1/3 сағ. кем
4) Есептегі шамалар қалай байланысқан?
s=v·t, v 1 - v 11 =3, t 1 -t 11 =1/3.
- арқылы қай шаманы белгілеген дұрыс?
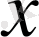 арқылы екінші жолаушының қозғалыс жылдамдығын белгілеп көрейік, сонда шамалар арасындағы баолық белгілі тәуелділіктерді 2-кестедегідей өрнектейміз.
арқылы екінші жолаушының қозғалыс жылдамдығын белгілеп көрейік, сонда шамалар арасындағы баолық белгілі тәуелділіктерді 2-кестедегідей өрнектейміз.
- Теңдеу құру үшін қандай шартты пайдалану керек?
2-кестеде бірінші және екінші жолаушының қозғалыс уақыттарының айырымы қолданылмай қалды. Осы айырым бізге теңдеу құруға қажет.
27
t
1
-t
11
=1/3 болғандықтан,
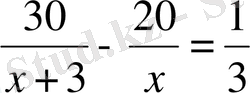 болады.
болады.
Теңдеудің сол жағындағы бөлімдердің ортақ бөлгішін ескере отырып (x≠3 және х≠0), алынған теңдеуден квадраттық теңдеуге ауысамыз:

Бұдан
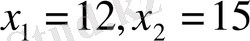 . Екі түбір де ортақ бөлгішті қанағаттандырады. Бұлардың қайсысы 2-жолаушының жылдамдығы болады: 15км/сағ. немесе 12км/сағ. Екі жауап та есептің шартын қанағаттандырады. Демек, екі жағдай қарастыру керек:
. Екі түбір де ортақ бөлгішті қанағаттандырады. Бұлардың қайсысы 2-жолаушының жылдамдығы болады: 15км/сағ. немесе 12км/сағ. Екі жауап та есептің шартын қанағаттандырады. Демек, екі жағдай қарастыру керек:
а) 2-жолаушының жылдамдығы 15км/сағ. болсын, сонда
 (сағ. ) және
(сағ. ) және
 (сағ. ) болады;
(сағ. ) болады;
б) 2-жолаушының жылдамдығы 12км/сағ. болсын, сонда
 (сағ. ) және
(сағ. ) және
v (сағ. ) болады.
Жауабы:
а) 1-жолаушының қозғалыс уақыты
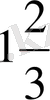 сағ., ал
сағ., ал
2-жолаушынікі
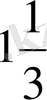 сағ. ; б) 1-жолаушының қозғалыс уақыты
сағ. ; б) 1-жолаушының қозғалыс уақыты
 сағ., ал
сағ., ал
2-жолаушынікі
 сағ.
сағ.
Соңғы сұраққа тоқталған дұрыс.
- Алынған теңдеуді шешу оңай ма?
Иә, себебі құрылған теңдеу стандартты. Ал, егер оқушылар
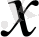 арқылы 1-жолаушының қозғалыс уақытын белгілесе, онда келесі теңдеу шығар еді:
арқылы 1-жолаушының қозғалыс уақытын белгілесе, онда келесі теңдеу шығар еді:
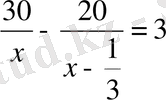 .
.
Бұл теңдеудегі бөлшектердің біреуінің бөлімінде бөлшек бар, ол теңдеуді түрлендіргенде қиындық туғызады.
3. 3. Есеп. Екі сортты бояу сатып алынды. Бірінші сортты бояуды - 3тг, ал екінші сортты бояуды - 2тг сатып алынды. Екінші сортты бояудан бірінші сорттыға қарағанда 2кг артық алынды, және екінші сортты бояудың 1кг -ы бірінші сортты бояудың 1кг -нан 1тг арзан. Бірінші сортты бояудан қанша кг сатып алынды?
Сұрақтарға жауап:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz