Автоматты басқару жүйелері: кибернетика, элементтер және статикалық-динамикалық модельдер


КІРІСПЕ
ПӘН ТУРАЛЫ ҚЫСҚАША МАҒЛҰМАТ:
Кибернетика дегеніміз - басқару және байланыс жөніндегі ғылым. Бұл ғылымның қолданбалы жағын кез-келген ғылыми зерттеу бағыттарына жатқызуға болады, ал оның теориялық мәні тікелей ешбір ғылымдармен байланыспайтын, бірақ олардың бәрінде де қолданылатын жалпы басқару теориясы болып есептеледі.
Басқару - кез-келген жүйенің ажырамайтын қасиеті. Бір-бірімен байланыстағы бөліктердің жиынтығын жүйе деп атайды.
Шын мәнінде, әлем кеңістігінің өзі көптеген, бір-бірімен байланыстағы кішігірім жүйелерден тұрады. Сол себептен «жүйе» деген ұғымға қатаң анықтама беру оңай емес.
Жүйені күрделілік дәрежесі бойынша жай динамикалық және күрделі жүйе деп жіктейді. Тармақталған құрылымымен және көптеген ішкі байланыстарымен жай динамикалық жүйеден ерекшеленетін жүйелерді күрделі деп атайды. Сонымен қатар жүйелерді детерминді және ықтималдық деп бөледі. Құрамындағы бөліктері алдын-ала қойылған болжам бойынша өзара әрекеттесетін жүйелерді детерминді дейді. Сол себептен, детерминді жүйелерді зерттеу кезінде ешбір анықталмағандық кездеспейді. Керісінше, ықтималдық жүйелер үшін алдын-ала дәл болжам жасау мүмкін емес. Сондықтан, бұл жүйелер күрделі жүйелер қатарына, яғни кибернетика ғылымының негізгі зерттеу саласына жатады.
Мұндай жүйелерді басқару үшін реттеуіш деп аталатын басқарушы механизм қолданылады. Реттеуіш - регулятор
- до^егпог, латынның «управляющий» (ді^егпаіог) деген сөзінен шыққан, ал ол өз кезегінде гректің «кибернесий»
- кормчий - (кеменің рөлін ұстап отыратын кісі) деген сөзінен пайда болган.
Барлық технологиялық объектілер басқарушы құрылғысымен бірге қайсыбір автоматты жүйені құрады, ал ол өз кезегінде автоматты басқару теориясы заңдарымен талданып, синтезделеді.
Сонымен, автоматты басқару (АБТ) және реттеу (АРТ) теориясы - автоматты реттеу жүйесін талдау, синтездеу тәсілдерін және құру принциптерін зерттейтін ғылым.
Автоматты реттеу теориясында шешілетін, автоматты реттеу жұйесінің объект параметрлерін тұрақтандыру мәселесі, АБТ жалпы мәселесінің дербес тұрі болып саналады.
АБТ басқару жүйесінің элементтерінің жұмыс істеу теориясымен бірге, автоматика деп аталатын, ғылымның кең тармағын құрады. Автоматика (гректің «Автоматос» деген сөзінен аударғанда - самодвижущийся, яғни «өздігінен әрекет ететін») өз кезегінде техникалық кибернетиканың бір бөлігі. Техникалық кибернетика, техникалық процестің (ТПАБЖ) және өндірістің автоматтандырылған басқару жүйесін (ӨАБЖ) құру мәселелерін қарастырады.
Автоматты басқару теориясының дамуына бірнеше атақты ғалымдар үлес қосты. Санкт-Петербург техно- логиялық институтының профессоры И. А. Вышнеградский 1877 жылы автоматты реттеу теориясының негізін қалады. Автоматты реттеу теориясының бұдан ары дамуы А. М. Ляпуновтың, әсіресе орыс авиациясының атасы атанған профессор Н. Е. Жуковскийдің еңбектерінде көрініс тапты. Олар автоматты басқарылатын машиналар мен механизмдерде өтетін процестердің математикалық теориясын жасады.
Қазіргі кезеңдегі АБТ дамуына академиктер Б. Н. Петров, В. С. Пугачев, А. А. Воронов, С. В. Емельянов, Я. З. Цыпкин және профессор В. В. Солодовников өз еңбектерімен елеулі үлес қосты.
Қазіргі уақытта АБТ, басқарудың жалпы теориясымен қоса, өндірісті басқаруды автоматтандыру және жетілдіру мәселелері де ерекше орын алады. Халық шаруашылығының барлық салаларына жоғары техниканы, ғылымның жетістіктерін кеңінен енгізу негізінде өндірісті өсіріп, жетілдіру Республикамыздағы негізгі мәселе болып отыр. Бұл міндетті жүзеге асыру жолында АБТ рөлі орасан зор. Өкінішке орай бұл бағытта күні бүгінге дейін бірде-бір қазақ тілінде жазылған оқу құралы жарық көрмеген. Сондықтан, белгілі орыс ғалымдарының еңбектерін және авторлардың көптеген жылдар бойы аудиторияларда оқыған лекциялық материалдарын негізге ала отыра жазылған бұл оқулықты сәйкес мамандықтар бойынша қазақша оқып жүрген студенттерге жеңілдік болсын деген ниетпен ұсынамыз.
Сөз соңында айтылар жағдай, бұл кітап қазақ тілінде тұңғыш жарық көріп отырған оқулық болғандықтан, оның кемшіліктері де болуы мүмкін. Оқулықтың авторлар ұжымы оқырмандардан келесі басылымның сапасын жақсартуға септігін тигізетін объективті пікір айтып, шынайы баға беруін зор алғыспен күтеді.
1. Лекция
Тақырыбы:АВТОМАТТЫ БАСҚАРУ ЖҮЙЕЛЕРІ ЖӘНЕ ОБЪЕКТІЛЕРІ
1. 1 Негізгі ұғымдар мен анықтау
Кез келген өндірісте технологиялық процестер белгілі бір мәнде шектетілетін физикалық шамалармен сипатталады. Жабдықтардың жұмысы кезінде ол шамалар белгілі бір деңгейде тұрақтануы, не берілген программа бойынша өзгеріп отыруы тиіс. Кез келген қондырғыда технологиялық процестің бірқалыпты жүруі белгілі бір ереженің, қызмет алгоритмінің орындалуына байланысты болады. Осы қызмет алгоритмін орындау үшін белгілі бір сыртқы команданы орындайтын қондырғыны, не машинаны басқару объектісі дейді.
Технологиялық процесті жүргізу үшін басқару объектісіне әсер ететін тиімді ықпалды басқару дейді. Егер бұл басқару адамның қатысуынсыз жүзеге асса, оны автоматты, ал адамның қатысуымен болса қолмен басқару деп атайды. Жалпы технологиялық процестер орындалатын барлық өндіріс жабдықтары басқару обьектілеріне жатады.
Алайда технологиялық процестің өзі де басқару объектісі бола алады. Әр объектіде физикалық шаманың берілген мәнін тұрақтандырып, немесе оны берілген бағытта өзгертіп отыратын басқарғыш құрылғысы болады. Басқарғыш органы арқылы объектіге белгіленген қызмет алгоритмін орындауға мүмкіндік беретін арнайы әсерлер беріліп отырады. Технологиялық процесті берілген қызмет алгоритмі бойынша өткізу мақсатында объектіге сырттан берілетін арнайы нұсқаулар (ережелер) жиынтығын басқару алгоритмі дейді.
Басқару объектісіне басқару алгоритміне сәйкес әсер ететін кез келген техникалық құрылғы автоматты басқару қурылғысы делінеді.
Бір-бірімен байланысты және басқару алгоритміне сәйкес өзара әрекеттесе жұмыс жасайтын автоматты басқару кұрылғысы мен басқару объектісінің жиынтығы автоматты басқару жүйесі (АБЖ) деп аталады. Жұмыс барысында автоматты басқару жүйесіне әртүрлі ішкі және сыртқы әсерлер ықпал жасайды. Автоматты жүйенің бір бөлігінен келесі бөлігіне технологиялық процестің бірқалыпты өтуін қамтамасыз ететін әрекеттің тізбекті желісін құрайтын әсерді ішкі әсер деп атайды. Оларды басқарушы әсер дейді. Ал сыртқы әсер екіге белінеді. Технологиялық процестің тиянақты өтуіне қажет бірінші әсер қызмет алгоритміне сәйкес жүйе кірісіне беріледі де, жоспарланған немесе тапсырыс- тық әсер деп аталады. Ал, екінші әсер жүйеге немесе басқару объектісіне сыртқы ортадан беріледі. Ол жүйе жұмысында алдын ала еске алынбайды да, кездейсоқ сипатта болып, басқару процесін қиындатады. Сол себепті оларды қобалжытқыш әсер деп атайды.
Технологиялық процестің дұрыс өтуіне сәйкес басқарылатын шаманың берілген уақыт аралығында ұстап отыруга керекті мәнін алдын ала берілген мән деп, ал фактілі, яғни процестің өлшенген мәнін нақты (қазіргі) деп атайды. Реттелетін шаманың алдын ала жоспарланған және нақты мәндерінің арасындағы айырмасын келісілмеген (айырымдық) шама дейді.
Технологиялық жабдықтардың қай-қайсысы болма- сын тұрақты (тағайындалған) режимде жұмыс істеуі керек. Бірақ нақты пайдалану жағдайында әртүрлі сыртқы қозулардың әсерінен тағайындалған режим ұдайы бұзылатындықтан, технологиялық процестің параметрлері өзгереді. Сол себепті өндірістік жабдықтарды (басқару объектісін) басқарып отыру қажет, яғни басқарылатын шама қоздырушы әсердің ықпалына қарамастан берілген ереже (программа) бойынша өзгеретіндей дәл есеппен басқарушы әсерді қалыптастыру керек.
1. 2. Автоматты жүйе элементтері
Автоматты жүйе өзара байланысқан және белгілі бір қызмет атқаратын дербес конструкциялық элементтерден тұрады, оларды автоматика элементтері не құралдары деп атайды. Элементтерді жүйеде атқаратын қызметіне қарай салыстырушы, түзетуші, қабылдаушы, жоспарлаушы, түрлендіруші және атқарушы деп ажыратады.
Қабылдаушы элементтер не бастапқы түрлендіріп бергіштер (датчиктер) технологиялық процестердің басқарылатын шамаларын өлшейді де, оларды бір физикалық түрден екінші бір физикалық шамаға түрлендіреді (мысалы, термоэлектрлік термометр температура айырымын термоЭҚК-не түрлендіреді) .
Жоспарлаушы элементтер (баптау элементтері) арқылы жүйеге реттелетін шаманың Х 0 қажет мәні беріледі; оның нақты мәні осы берілген мәнге сәйкес келуі тиіс.
Салыстырушы элементтер реттелетін шаманың берілген мәнін Х 0 нақты мәнімен X салыстырады. Бұл элементтің шығысында алынатын айырымдық сигнал X = Х 0 -Х атқарушы элементке тікелей не күшейткіш арқылы беріледі.
Түрлендіруші элементтер сигналдың пайдалануға ыңғайлы түрге түрлендірілуін және оның қуатын магниттік, электрондық және т. б. күшейткіштер арқылы үдетуін жүзеге асырады.
Атқарушы элементтер басқару объектісіне берілетін басқару әсерін тудырады. Олар басқару объектісіне берілетін не одан алынатын энергия немесе заттар санын өзгерту арқылы басқарылатын шаманы берілген мәніне сәйкес етіп ұстап отырады.
Түзетуші элементтер басқару процесінің сапасын жақсарту үшін қажет.
Автоматты жүйелерде көрсетілген негізгі элементтерден басқа қосалқы элементтер де болады, оларға ауыстырып қосқыш құрылғылар мен қорғау элементтері, резисторлар, конденсаторлар, сигнал беру жабдықтары жатады.
Автоматика элементтерінің қолдану және технологиялық ерекшеліктерін айқындайтын арнайы сипаттамалары мен параметрлері болады.
Басты сипаттамалардың біріне элементтің статикалық сипаттамасы жатады. Статикалық сипаттама деп, тұрақталған режим кезіндегі Х шш шамасының Х кір шамасына тәуелділігін айтады:
. Кірістік шамасының таңбасына сәйкес бейреверсивті (шығыстық шаманың таңбасы өзгерістің барлық деңгейінде тұрақты болғанда) және реверсивті (кірістік шаманың таңбасының өзгерісі шығыстық шаманың таңбасының өзгерісіне әкеледі) статикалық сипаттамалар болып ажыратылады.
Динамикалық сипаттама элементтердің динамика- ЛЬ Қ режимде, яғни кірістік шаманың шапшаң өзгерген сәттеріндегі жұмысын бағалау үшін пайдаланылады.
Оны өтпелі сипаттамамен, беріліс функциясымен және жиілік сипаттамаларымен өрнектейді. Өтпелі сипатта- ма Х іт г шығыстық шаманың / уақытқа тәуелділігін көр- сетеді: Х кір кірістік сигналының секірмелі өзгерісі кезінде
Х шыг = /(і) .
Жалпы беріліс функциясына, өтпелі және жиілік сипаттамаларына төменгі тарауларда толыгымен тоқталатын боламыз.
Автоматика элементтерінің негізгі параметрлерінің қатарына беріліс коэффициенті мен сезімталдық деңгейі жатады.
Беріліс коэффициентін элементтердің статикалық сипаттамасымен анықтауға болады. Оны статикалық, динамикалық (дифференциалдық) және салыстырмалы коэффициенттер деп үш түрге ажыратады.
Х шыг шығыстық шамасының Х кџ кірістік шамасына қатынасын статикалық беріліс коэффициенті деп атай- ды, яғни К ст = Х шш /Х кп . Нақты конструкциялық эле- ментке қатысты статикалық беріліс коэффициентін, мысалы, күшейткіштерде - күшейту коэффициенті, редукторларда - редукция коэффициенті, трансформа- торларда - трансформация коэффициенті деп атайды.
Бейсызықты сипаттамасы бар элементтер үшін К о динамикалық беріліс (дифференциалдық) коэффициенті пайдаланылады, яғни коэффициенті элементтің X /X . шығыстық шамасының салыстырмалы өзгерісінің Х кі /Х кіі>іі кірістік шама- сының салыстырмалы өзгерісіне қатынасына тең:
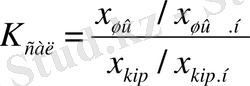
мұндағы X мен X . - шығыстық және кірістік шамалардың номинал мәндері. Бұл коэффициент өл- шемсіз шама, әрі конструкциясы мен қызмет әрекеті әртүрлі элементтерді салыстыруда тиімді.
Сезімталдық деңгей шығыстық шаманың айтар- лықтай өзгерісі байқалатын кірістік шаманың ең кіші мәні. Ол элемент конструкциясындағы тетіктер арасын- дағы үйкеліс, саңылау және люфтінің салдарынан болады.
Ауытқу бойынша басқару принципі пайдаланылатын автоматты тұйықталған жүйелердің артықшылығына кері байланыстың болуы жатады. Кері байланыс әрекетінің принципін электр қыздыру пешінің температурасын басқару жүйесі мысалы негізінде қарастырайық. Температураны берілген шекте ұстау үшін объектіге берілетін басқарушы әсердің, яғни қыздырғыш элементке түсірілетін кернеудің мәнін температураны ескере отырып өзгертеді. Температураның бастапқы түрлендіргіші арқылы жүйе шығысы оның кірісімен жалғастырылады. Мұндай қосылысты, яғни ақпарат (информация) басқарушы ықпалмен салыстырғанда кері бағытта берілетін каналды кері байланыс деп атайды. Кері байланыс оң және теріс, қатаң және икемді, негізгі және қосалқы болып ажыратылады.
Оң кері байланыс деп, кері байланыс әсері мен жоспарланған әсердің таңбалары дәл келетін байланысты айтады. Ал дәл келмеген жағдайда теріс кері байланыс делінеді.
Егер берілетін әсер уақыт өтуіне тәуелсіз болып тек реттелетін параметрдің мәніне ғана тәуелді болса, онда мұндай байланысты қатаң кері байланыс деп атайды. Қатаң кері байланыс жүйенің тұрақталған, әрі өтпелі режимдері кездерінде де әрекет етеді. Тек өтпелі режимде әрекет ететін байланысты икемді кері байланыс дейді. Икемді кері байланыс өзі арқылы уақыт өтуімен басқарылатын шама өзгерісінің бірінші не екінші туындысын өткізетіндігімен сипатталады. Икемді кері байланыстың шығысында сигнал тек басқарылатын шама уакыт барысында өзгергенде ғана пайда болады.
Негізгі кері байланыс басқару жүйесінің шығысын оның кірісімен қосады, яғни басқарылатын шаманы жоспарлау құрылғысымен байланыстырады. Ал қалған кері байланыстар қосымша не жергілікті деп аталады. Қосымша кері байланыс жүйенің қайсыбір буынынан алынған әсер сигналын алдыңғы тізбектегі кез келген басқа бір буынның кірісіне береді. Мұндай байланыс жеке элементтердің қасиеті мен сипаттамасын жақсарту үшін пайдаланылады.
1. 3. Автоматты басқару жүйесінің құрылымы
Автоматты басқару жүйесі құрылымы жағынан әр түрлі болуы ықтимал. Жалпы жағдайда бұл құрылымға белгілі бір ерекше қасиеттерімен және аралық әсер беру жолдарымен жіктелген автоматты жүйені түзетін Дербес бөліктердің жиынтығы жатады. Автоматты басқару жүйесінің алгоритмдік, функционалдық және конструкциялық құрылымдары болады.
Автоматты басқару жүйесінің алгоритмдік құрылымы деп, әр бөлігі ақпаратты түрлендірудегі белгілі бір алгоритмді орындауға арналған құрылымды айтады.
Сигналды түрлендірудің элементар алгоритміне сәйкес келетін автоматты жүйенің алгоритмдік құрылымының бір бөлігін элементар алгоритмдік буын деп атайды. Әрбір элементар буын бір ғана математикалық немесе логикалық операцияны орындайды. Схемада элементар буынды ішінде сигналды түрлендіруге сәйкес оператор жазылған тікбұрышпен кескіндейді. Кей кезде оператордың орнына шығыстық сигнал мен кірістік сигнал аралығындағы байланысты көрсететін график немесе өтпелі функция қисығы көрсетіледі.
Элементар буындар статикалық, динамикалық, арифметикалық және логикалық болып ажыратылады. Статикалық буынның шығыстық сигналының лездік мәні кірістік сигналдың уақыт ағымындағы өзгеруінің сипатына емес, оның тек осы мезеттегі мәніне ғана тәуелді болады. Статикалық буын ретінде, мысалы, екіпозициялық релені алуға болады (2. 1, а-сурет) . Суретте реленің кірістік және шығыстық сигналдарының өзгеру графигі де көрсетілген.
НМЕС"әндеріне де, яғни кірістік сигналдың өзгеру сипатына тәуелді. Динамикалық буынның мысалы ретінде диф- ференциалдауыш буынды алуға болады (2. 1, б-сурет) .
Арифметикалық буын қосу, алу, көбейту, бөлу арифметикалық амалдарының біреуін іске асырады. Автоматикада, сигналдарды алгебралық қосынды- лайтын арифметикалық буын, қосындауыш (2. 1, в-сурет) жиі қолданылады. Суретте сонымен бірге электрлік (гальваникалық) және магниттік сигналдарды да қосындылау мысалдары келтірілген.
Логикалық көбейту («ЖӘНЕ»), қосу («НЕМЕСЕ»), логикалық теріс-теу («ЕМЕС») және т. б. логикалық операцияларды орындайтын буынды логикалық деп атайды. Жалпы логикалық буынның кірістік және шығыстық сигналдары дискретті болады да логикалық айнымалылар ретінде қарастырылады (2. 1, г-сурет) .
Автоматты басқару жуйесінің фунционалдық құрылымында әрбір бөлік белгілі бір қызметті атқарады. Қызмет ретінде автоматты басқарушы құрылғының ақпарат алу, оны өңдеу, т. б. осы секілді негізгі қызметін, сонымен бірге сигналды беру, оларды салыстыру, ақпа- ратты беру түрін өзгерту тәрізді дербес қызметін айтуға болады.
Егер автоматты басқару жүйесі құрылымының әр бөлігі жеке конструкциялық тұтастық құратын бөлік болса, ондай құрылымды конструкциялық кұрылым деп атайды.
Басқару жүйесінің құрылымын график бойынша кескіндеуді қурылымдық схема дейді. Белгілі бір ерекшеліктерімен топталған автоматты жүйе бөлігін график түрінде, ішінде бұл жүйенің оның қандай бө- лігі екендігін білдіретін шартты белгісі бар төртбұрышпен кескіндейді. Автоматты жүйенің бөліктерінің арасында берілетін әсер жолын, сол әсер берілетін бағыт бойымен бағыттауыш сызықпен кескіндейді.
Автоматты басқару жүйесінің, не автоматты құрылғының құрылымдық схемасындағы бөліктері арасын- дағы берілетін әсердің бағыты мен жолын көрсететін
қарапайым құрамдас бөлігін қурылымдык, схеманың байланысы деп атайды.
Автоматты жүйенің құрылымдық схемасының байланысы негізгі, қосымша және кері байланыстар болып ажыратылады.
Негізгі байланыс деп, автоматты басқару жүйесінің негізгі тізбегі бойындағы бөліктерінің арасындағы түзілетін байланысты айтады.
Қосымша байланыс деп, негізгі тізбекке не оның қайсыбір бөлігіне қосалқы түрде әсер берілу жолын түзетін автоматты басқару жүйесінің құрылымдық схемасының байланысын айтады.
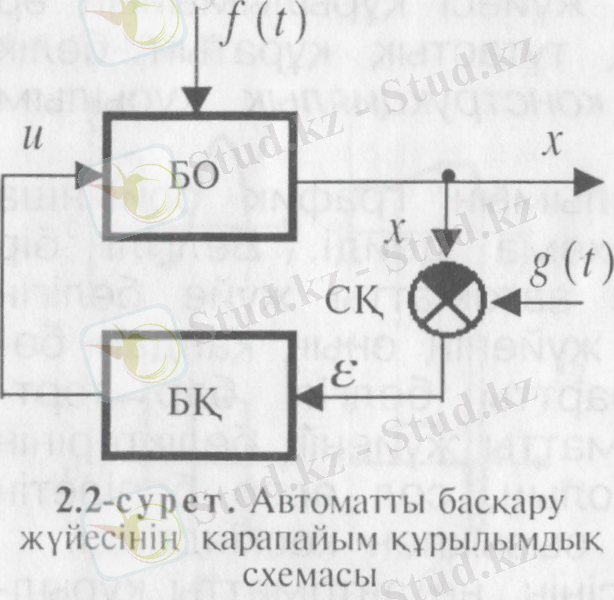
Мысал ретінде 2. 2-суретте басқару объектісінен (БО), басқарушы (БҚ), және салыстырушы (СҚ) құрылғысынан тұратын автоматты басқару жүйесінің қарапайым құрылымдық схемасы көрсетілген. Автоматты басқару жүйесінің кірісі және шығысы болады.
Кіріс деп, сырттан жүйеге не құрылғыға, оның жеке бөліктеріне тікелей әсер берілетін автоматты басқару жүйесінің әсер тізбегінің бөлігін айтады. 2. 2-суретте әсер беру тізбегінің бір бөлігі жүйенің 8(0 жоспарлау әсері берілетін кірісі де, екінші бөлігі (0 қоздыру әсері берілетін кірісі.
Шығыс деп, автоматты жүйеде не оның элемент- терінде қызмет алгоритміне сәйкес қалыптасқан әсерді сырт жаққа беретін автоматты басқару жүйесінің әсер тізбегінің бөлігін айтады. 2. 2-суретте X автоматты басқару жүйесінін шығысы.
Автоматты басқару жүйесінің әсер тізбегі деп ішкі және сыртқы әсерлер берілетін жеке жолдардың жиынтығын айтады. өңры- лымдық схемада әсер тізбегінің жеке жолдары тұтас және бағыттауыш сызықтармен кескінделеді.
Автоматты басқару жұйесінің не оның қарастырылатын бөлігінің шартты түрде бөлінген, кірісінен шығысына қарай бағытталған әсер тізбегін жүйенің негізгі әсер тізбегі деп атайды.
Негізгі әсер тізбегі автоматты жүйені немесе жүйе бөлігін қандай мақсат үшін пайдаланатынына қарай іріктелінеді.
Жалпы алғанда автоматты жүйенің басқарушы құрылғысы негізгі әсер тізбегіндегі фукнционалды құрылғысынан (ФҚ), қосымша байланыс құрылғысынан (ҚБҚ) және қосымша кері байланыс құрылғысынан /ҚҚБҚ) тұрады. Басқарушы құрылғы өзінің шығыс тізбегінде тұрған атқарушы тетікке (АТ) әсерін тигізеді, я ол өз кезегінде реттеуші орган (РО) арқылы басқарылатын объектіге (БО) әсер етеді. Басқарылатын шама өлшеуіш құрылғысымен (ӨҚ) өлшенеді.
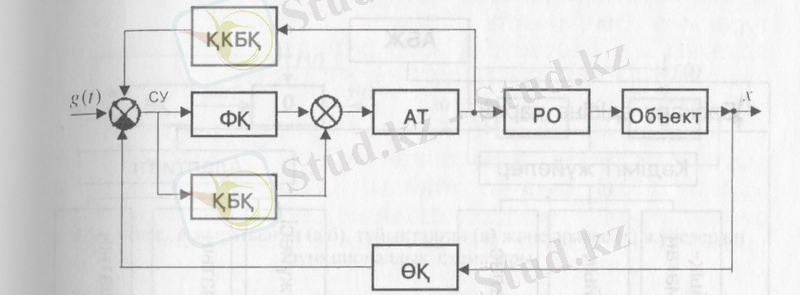
2. 3-сурет. Автоматты басқару жүмесінің жалпы функционалдық
схемасы
Сонымен, жалпы жағдайда автоматты реттеу жұйе- сінің құрылымын атқарушы тетігінде қосымша байланыс тізбегі бар, 2. 3-суретте келтірілгендей функционалды схема түрінде көрсетуге болады.
2-Лекция
Тақырыбы: Статикалық және динамикалық модельдері мен олардың үзбелері
Жоспар: 2. 1АБЖ статикасы. Статикалық сипаттамалар және статикалық буындар
Екі және одан да көп элементтердің тізбектеле қосылуы
Буындардың параллель қосылуы.
Кері байланыспен қамтылған жүйе
2. 2. Реттеу статизмі
2. 3. Статикалық сипаттамаларды коррекциялау
2. 1. Екі және одан да көп элементтердің тізбектеле қосылуы. Бұл жағдайда бір элементтің шығысы екінші элементтің кірісі болып буындар тізбегін құрайды. 3. 3 - суретте үш тізбектеле қосылған буындардан тұратын жүйенің статикалық сипаттамасын салудың графикалық әдісі көрсетілген. Бірінші квадранттың абсцисса осіне бірінші буынның х,, ал ординатасына
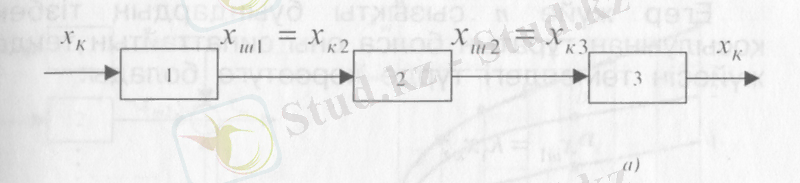
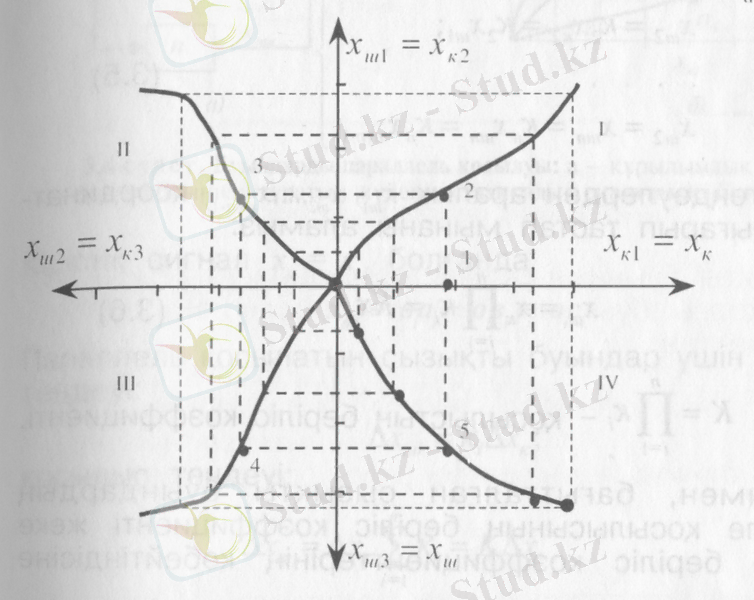
2. 1-сурст. Буындарлын тізбектелс косылуы:
а - кұрылымдык схсма; б - статикалык сипаттаманы тұргызу.
Мәндері салынады да, бұл квадрантта бірінші буынның статикалық сипаттамасын тұрғызамыз. Екінші квадранттың вертикаль осіне х к2 = х ш , ал горизонталь осіне
мәндері салынып, бұл квадрантта екінші буынның сипаттамасы тұрғызылады. ұшінші квадранттың горизонталь осіне х
= х ш2 , ал вертикаль 0сіне х ш3 = х ш мәндері салынып, ұшінші квадрантта үшінші буынның статикалық сипаттамасы тұрғызылады.
Егер жүйе буындарының саны үштен көп болса, онда олар жеке-жеке топтарға бөлінеді де, әр топтың сипаттамалары ізделінеді. Соңынан әр топты бір суын деп альп, жүйенің толық сипаттамасы салынады. Егер жұйедегі буындар саны тек екеу-ақ болса, онда үшінші квадранттағы буынды беріліс функциясы бірге тең, яғни сипаттамасы биссектриса тұрінде болатындай етіп алады.
6
Егер жүйе п сызықты буындардың тізбектеле қосылуынан тұратын болса оны сипаттайтын теңдеулер жүйесін төмендегі түрде көрсетуге болады:
х
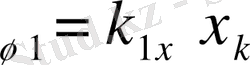
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz