Симплекс әдісінің геометриялық түсінігі, алгоритмі және тәжірибелік қолданылуы


Мазмұны
І Кіріспе . . . 3
ІІ Симплекс әдісі
2. 1 Симплекс әдісінің геометриялық түсінігі . . . 5
2. 2 Қысқаша симплекс әдісінің шығу тарихы . . . 9
ІІІ Симллекс әдісінің алгоритмі
3. 1 Симплекс әдісінің мақсаты мен идеясы . . . 11
3. 2 Тәжірибелік есептерді симплекс әдісімен шығару . . . 19
ІV Қорытынды . . . 26
V Пайдаланылған әдебиеттер . . . 27
Кіріспе
Симплекс - ағылшын сөзі, кеңістікгегі қарапайым көпбұрышты көп жақты бейне, оның бұрыштарының координаттары ізделініп отырған белгісіздердің оптималды мәндеріне сәйкес.
Симплекс әдісінің негізгі мақсаты - егер мақсат фунция максимумге ізделінсе, онда алғашқы табылған төбеден келесі тебеге жылжығанда кез келген төбеге емес , мақсат функцияның мәні өсетін тебеге жылжуды қамтамасыз ету. (Егер есеп минимумге ізделінсе, онда алғашқы мақсат функцияның мәнінен кейінгі мәні кіші болуын қамтамасыз ету) .
Симплекс әдісін қолданғанда бір төбеден екінші төбеге көшкенде белгілі бір бағытта жоспарлы түрде көшіледі, бұл жағдайда кейбір «керексіз» көпжақтының төбелері қарастырылмай қалып қалады да, есептің шешу жұмысы ұтымды, жедел жүргізіледі. Симплекс әдісінің қарапайым гоеметериялық интерпретациясы анық көрсетілген, егер оптималдық төбеге көрсетілген стрелка бағытымен жылжысақ онда осы бағыттан тысқары қалған төбелер қарастырылмайды. Симплекс әдісін графиктік жолмен іске асырғанда осы айтылған жағдайларды графиктен көзбен көруге болады. Бірақ мұндай жұмыстар белгісіздердің саны үштен көп болғанда қиындайды да, тіпті оларды орындау мүмкін емес. Мұндай кездерде тек ойша тұжырымдарға ғана сүйенуге тура келеді . Сонымен қатар графиктік жолмен шығатын есептердің тәжірбиелік есептерге қарағанда мүмкіндіктері аз, маңызы және мәнісі төмен. Сондықтан сызықты программалау есептерін симплекс әдісімен шешудің математикалық алгоритмдерінің маңызы үлкен.
Курстық жобаның мақсаты: Симплекс әдісінің геометриялық әдістерін қолданудың тиімді жолдары:
Зерттеу міндеттері: Универсал Симплекс әдісі теориясының есептеу алгоритмі, қысқаша симплекс әдісінің шығу тарихы, симллекс әдісінің алгоритмі, симплекс әдісінің мақсаты мен идеясы туралы толық мағлұмат беру.
Зерттеу объектісі: Универсал Симплекс әдістерін қолданып есептердің алгоритмін тұрғызу жолдары.
Зерттеу пәні: Өндірістік және экономикалық процестерді модельдеу.
Зерттеу әдістері: Ғылыми әдістемелік оқулықтар, журналдар, жаңа ақпараттық технологиялар.
Курстық жобаның құрылымы: Кіріспеден, негізгі бөлімнен, қорытындыдан, қосымша және пайдаланылған әдебиеттерден тұрады.
ІІ Симплекс әдісі
2. 1 Симплекс әдісінің геометриялық түсінігі
Графиктік әдіс сызықты программалау есептері тек екі белгісізден ғана құрылғанда қолданылады, ал есеп үш белгісізден асса, онда мұндай есептерді графиктік жолмен шешу қиынға соғады. Теория жүзіндө екі және үш белгісізі бар есептерді графиктік жолмен шешкен сияқты кез келген белгісізі бар есептер де графиктік жолмен шешіледі деп қарастыруға болады. Өйткені егер белгісіздің саны екеу болса, есептің анықталу аймағы жазықтықта жатқан дөңес көп бұрышты береді. Егер белгісіздің саны үшеу болса, онда есептің анықталу аймағы кеңістікте жатқан үш өлшемді дөңес көп жақтыны береді. Егер шектеуші шарттар мынадай белгісізден тұрса:
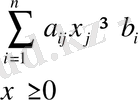
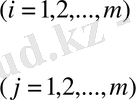
онда осы шектеулер арқылы құрастырылған М аймағын, 1-ширектегі n - өлшемді кеңістіктегі өлшемі n болатын дөңес көпжақты деп қарастыруға болады. Бұл жағдайда мақсат функциясы
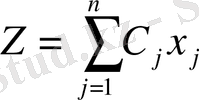
Z-дің кез-келген тұрақты мәнінде n - өлшемді гипержазықтық.
Симплекс әдісінің мән-жайын тереңірек түсіну үшін алдыңғы тақы-рыптағы кейбір белгілі қағидаларды тағы да еске түсірейік. Мысалға, егер Z-дің мәні -∞ тен +∞ дейін өзгерсе, онда гипержазықтық өзіне-өзі параллель жылжи отырып, М дөңес көпжақтыға жетеді де, онымен бір нүктеде (немесе бір қабырғасының үстіне түседі) қиылысады, бұл нүкте «ену» нүктесі делінетіні алдыңғы тақырыпта айтылды. Гипержазықтықты және өзіне - өзін параллель етіп, М аймағы бойынша жылжыта берсек
Z-дің бір мәнінде, ол гипержазықдық М аймағы соңғы нүктесімен жанасады да (бұл нүкте "шығу" нүктесі делінетіні белгілі), осыдан кейін М аймағынан шығып кетеді. Бұл түсініктерден кейін симплекс әдісінің геометриялық мағынасына қысқаша тақталайық. Біріншіден, алдыңғы тақырыптарда айтылғандай егер сызықты программалау есептерінің оптималды шешімі болса, ол шешім дөңес көпжақты М аймағының төбелерінің біріңде жатады деген теорема белгілі. Екіншіден, мақсат функцияның графигін құрғанда, Z=d деп қарастырдық, бұл жағдайда (-∞< < + ∞) d-нің мәніне байланысты гипертүзу (гипержазықтық), яғни есептің анықталу аймағы М дөңес көпбұрышынан әлде қайда алыста жатуы мүмкін. Тәжірибелік есептерді шешкенде мұндай жағдай көп қосымша есептеулер жүргізуді қажет етеді. Сондықтан бұл екі тұжырымды (шешім қабылдауды) тереңірек талқылайық.
Талқылауды екінші ұғымнан бастайық. Мақсат функцияның жылжу бағыты оның алғашқы құрылуына байланысты, өйткені кейінгілері сол бұрынғы графикке параллель болып келеді. Егер Z-дің алғашқы графигі дұрыс құрылмаса, тікелей өзіне-өзін параллель жылжытудың нәтижесінде нақтылы олтималды шешім ала алмауымыз мүмкін.
Енді Z-дің алғашқы графигін тәжірибе жүзінде қалай құратынын түсіндірейік. Ол үшін екі белгісізі бар есепті қарастыралық:
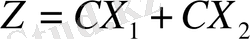
Егер Z = d = 0 десек теңдеудің графигі координат осінің бас нүктесінен өтетінін байқаймыз. Бірақ бір нүкте арқылы шексіз түзулер жүргізуге болады деген геометриялық теорема бойынша олардың ішІнен бізге қажетті біреуін ғана тауып алу қажет. Оны табу үшін қарастырылып отырған түзу сызықХ1 және Х 2 өстерімен қандай бұрыш жасайтынын анықтау керек, яғни Z(х 1, х 2 ) - функциясының градиентін іздеу қажет, сонымен қатар табылған градиент осы түзу сызықтың жылжу бағытын көрсететіні 3-бөлімде айтылды. Берілген функция үшіy Z(Х1, X2) = С 1 Х 1 + С2 X2 оның градиенті мына формуламен есептелінеді
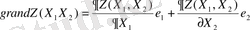
мұндағы
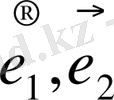 сәйкес остердегі бағыттаушы бірлік векторлар, ал
сәйкес остердегі бағыттаушы бірлік векторлар, ал
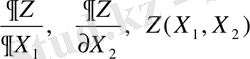 - функцияның Х1жәнө Х 2 бойынша сызықты дербес туындылары.
- функцияның Х1жәнө Х 2 бойынша сызықты дербес туындылары.
Z(Х 1, Х 2 ) - функцияның Х1және Х 2 белгісіздері бойынша сызықты функция болғандықтан:
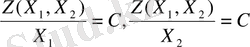
деп есептеп градиентті былай өрнектейік:
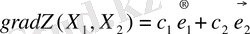
Градиенттің ұзындығы мына формуламен есептелінеді:
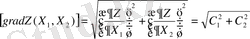
Сонымең бағыттаушы векторы n десек, онда:
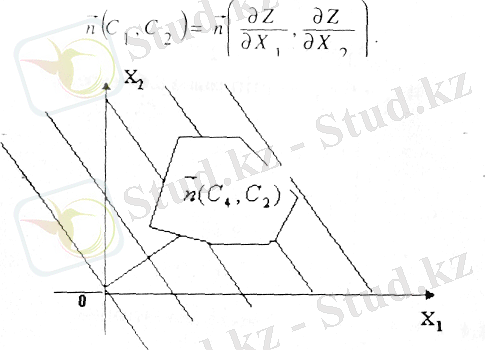
1 - сурет.
Енді 1-теоремадағы ұғымды қайта еске түсірелік. Теореиа бойынша Z мақсат функцияның оптималды мәнін табу үшін М-дөңес көпбұрыштарының барлық төбелерін қарастыру керек, ол ушін әр кезде бір төбеден екінші төбеге жылжып отыру қажет. Кейде Z - түзуі өзіне-өзі параллель жылжьіғанда кейбір төбеден өтпей қалуы да мүмкін. Бір төбеден келесі төбеге жедел көше отырып, оптималды мән беретін төбене іздеп табу қажет. Сөйтіп осы баяндалған геометриялық әрекеттер симплекс әдісінің негізін құрайды.
Симплекс - ағылшын сөзі, кеңістікгегі қарапайым көпбұрышты көп жақты бейне, оның бұрыштарының координаттары ізделініп отырған белгісіздердің оптималды мәндеріне сәйкес. Көп өлшемді геометрияда
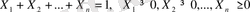
шарттарын қанағаттандыратын
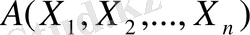 нүктесінің геометриялық орны симплекс делінеді.
нүктесінің геометриялық орны симплекс делінеді.
Симплекс әдісінің негізгі мақсаты - егер мақсат фунция максимумге ізделінсе, онда алғашқы табылған төбеден келесі тебеге жылжығанда кез келген төбеге емес , мақсат функцияның мәні өсетін тебеге жылжуды қамтамасыз ету. (Егер есеп минимумге ізделінсе, онда алғашқы мақсат функцияның мәнінен кейінгі мәні кіші болуын қамтамасыз ету) .
Сонымен, симплекс әдісін қолданғанда бір төбеден екінші төбеге көшкенде белгілі бір бағытта жоспарлы түрде көшіледі, бұл жағдайда кейбір «керексіз» көпжақтының төбелері қарастырылмай қалып қалады да, есептің шешу жұмысы ұтымды, жедел жүргізіледі. Симплекс әдісінің қарапайым гоеметериялық интерпретациясы анық көрсетілген, егер оптималдық төбеге көрсетілген стрелка бағытымен жылжысақ онда осы бағыттан тысқары қалған төбелер қарастырылмайды. Симплекс әдісін графиктік жолмен іске асырғанда осы айтылған жағдайларды графиктен көзбен көруге болады. Бірақ мұндай жұмыстар белгісіздердің саны үштен көп болғанда қиындайды да, тіпті оларды орындау мүмкін емес. Мұндай кездерде тек ойша тұжырымдарға ғана сүйенуге тура келеді . Сонымен қатар графиктік жолмен шығатын есептердің тәжірбиелік есептерге қарағанда мүмкіндіктері аз, маңызы және мәнісі төмен. Сондықтан сызықты программалау есептерін симплекс әдісімен шешудің математикалық алгоритмдерінің маңызы үлкен.
Осы алгоритмдерді қарастырмас бұрын симплекс әдісіне байланысты аздаған қысқаша тарихи мәліметтерге тоқталайық.
2. 2 Қысқаша симплекс әдісінің шығу тарихы
Жалпы математикалық программалау пәні өмірдің қажеттілігінен
пайда болған қолданбалы математиканың негізгі бөлімі. Жоғарыда айтылғандай математикалық программалаудың ішіндегі барлық халық шаруашылығына көп таралғаны, әртүрлі әдістері терең зерттелген бөлім сызықты программалау әдістері болып есептелінеді. Математикалық программалау пәнінің ең негізгі бөлімі сызықты программалау есептерді дүние жүзінде бірінші рет 1930 жылдары жарық көрді. Сызықты программалау есептері басқа тәжрибелік есептерге қарағанда өте қарапайым
,
зерттеуге ыңғайлы.
Сызықты программалаудың дербес есебінің бірі-қатынас есебінің дербес түрі 1931жылы Венгрияда басылып шықты, бұл мақаланың авторы математик Эгервари болатын. Кейінірек келе бұл мақаланың негізінде бірнеше еңбектер жазылады. Бұған мысал үшін 1951 және 1956 жылдары жарыққа шыққан КунХ. В. жәнеТаккерА, В 1957ж. жазылған Форд Х. Р. және Фалкерсон Д. Р. еңбектерін алуға болады. Бұл еңбектерде қатынас есептерін шөшуге арналған әдістер көрсетілген кейін келе әдебиетерде бұл әдісті қатынас есептерін шешудегі Венгер әдісі дейтін болды.
Сызықты программалау атты термин алғаш рет 1940 жылдары АҚШ-та қолданылды. Сызықты программалау әдісінің арнайы есептерінің бірі 1941 жылы АҚШ-та басылып шықты, оның авторы Хичкок Ф. Л. бопатын.
Бұрынғы Кеңестер Одағында сызықты программалау әдісінің негізін қалаушы академик Л. В. Канторович болды. Себебі оның көптеген сызықтық программалау әдістеріне арналған дербес есептері 1930 жылдардан бастап жарыққа шыға бастады. 1956 жылы Дж. Данциг, X. Р. Форд және Д. Р. Фалкерсон Венгер әдісінің негізінде сызықты программалаудың есептерін шешуге арналған, Л. В. Канторович ұсынған потенциал әдісіне өте сәйкес әдіс ұсынды. Ал 1947 жылы Дж. Б. Данциг сызықтық программалау әдістерінің ішіндегі әмебап симплекс әдісін жарыққа шығарды. Бірақ бұл әдістің Л. В. Канторовичтың 1939 ж. ұсынған, біртіндеп жақсарту әдісінен айырмашылығы өте аз болатын. Өкінішке орай бұл әдісті Л. В. Канторович бұрын үсынса да көптеген әдебиеттерде, оқулықтарда симплекс әдісін Дж. Данциг әдісі деп атайды.
ІІІ бөлім. Симллекс әдісінің алгоритмі
3. 1 Симплекс әдісінің мақсаты мен идеясы
Симплекс әдісінің мақсаты мен идеясын толық түсіну үшін есепті жалпы түрде қарастырып, әдісті тәжірибелік есептерге қолдану жолын қарастырайық. Ол үшін ең алдымен сызықты программалау есептерінің жалпы моделінің мәнісіне тоқталайық. Төмендегі шектеуші шарттарды қанағаттандыратын:
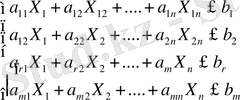 (3)
(3)
(4)
Мына мақсат функцияның ең үлкен (оптималдық) мәнін табу керек делік:
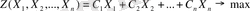 (5)
(5)
Біз жоғарыда симплекс әдісінің геометриялық мағынасын қарастырғанда, ең алдымен және шектеуші шарттар бойынша М дөңес көпжақтысын құрып, оның бір төбесін (есептің алғашқы базистік шешуін) тауып, сол төбедөн градиент арқылы мақсат функция кемімейтіндей (егер есеп ең кіші мәнге берілсе мақсат функция артпайды) етіп жылжыта отырып, ең үлкен мән беретін төбеге жетеміз деген едік. Міне осы идеяны матиматика түрінде қарастырамыз.
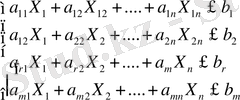 және
және
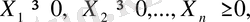
теңсіздіктер берілгендіктен математика тілінде есептің анықталу аймағы берілді деп есептейміз. Ал енді біз оптималдық төбеге қарай жылжу үшін ең алдымен есептің барлық шектеуші шарттарын орындайтын алғашқы шешуді табу керек. Ол үшін теңсіздіктердің әр қайсысының сол жағына y(i=1, 2…m) санын қосып теңдікке айналдырамыз.
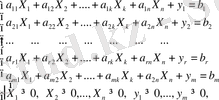
Экономикалық мағынада У 1 , У 2 , . . . , У m - дер сәйкес 1, 2, . . . және m - қордың қолданылмаған (өндіріске түспеген) мөлшерін береді. Егер есепті шешу нәтижесінде Y 1 =0, Y 2 =0, …, Y m =0 болса, онда барлық қорлар толығымен өндірісте қолданылған. Бірақ іс жүзінде барлық қордың берілген мөлшері бірден толық пайдаланбауы да мүмкін. Ал У 1 , У 2 , . . . , У m - пайдаланылмаған қор мөлшерін беретіндіктен өндіріске еш пайда келтірмейді, демек мақсат функцияда олардың (У 1 , У 2 , . . . , У m ) коэффиценттері нөлге тең болады, яғни

Сонымен есеп берілген шарттар оырндалған жағдайдағы
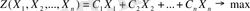 функцияның ең үлкен мәнін беретін шешуді іздеуге бағытталған. Егер теңдікті y(i=1, 2…m) арқылы шешетін болсақ:
функцияның ең үлкен мәнін беретін шешуді іздеуге бағытталған. Егер теңдікті y(i=1, 2…m) арқылы шешетін болсақ:
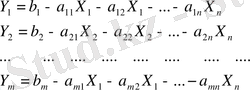 (6)
(6)
Мұндағы У 1 , У 2 , . . . , У m белгісіздері математика тілінде базизтік белгісіздер деп, ал Х 1 , Х 2 , . . . , Х n базистік емес белгісіздер деп аталады.
Демек базистік белгісіздер (векторлар) базистік емес белгісіздер арқылы өрнектеледі. Олай болса геометриялық мағынадағы симплекс әдісін мақсаты бір төбеден екінші төбеге көшу дегеніміз, бір базистік белгісіздер, екінші базистік белгісізге көшу керек деген ұғыммен сәйкес Егер Х 1 =0, Х 2 =0, …, Х n =0 десек, (6) теңдеуден Y 1 =b 1 , Y 2 =b 2 , …, Y m =b m
Экономикалық мағынасы b 1 (i=1, 2…m) қолда бар қордың мөлшері болғандықтан әрқашанда b 1 ≥0, (i=1, 2…m) ендеше Y j ≥0, Y j ≥0, …, Y j =b j ≥0 деген жағдай және тендеулерінің шешімін береді, бұл жағдайда мақсат функцияның мәні нөлге тең (Z=0), өйткені әлі ешқандай өнім өндірілген жоқ. Олай болса Х j =0, Y j =b j ≥0 шешу жағдайы есептің алғашқы шешімі бола алады. Демек, алғашқы төбе табылады, енді мақсат функциясының мәні кемімейтін келесі төбеге көшу керек. Бұл идеяны математикалық жолмен түсіндіру біраз қиынға түседі ол үшін біз оны кесте түрінде түсіндірелік. Негізінде сызықты программалау есептерінің шешімі симплекс әдісі бойынша бір кестеден, екіншіге одан үшіншіге т. б. кестелерге көшу арқылы табылады (латынша әрекетті әрекетті "Итерация", яғни бір әрекетті қайта-қайта қайталау дейді) .
Ақырғы теңдеулер арқылы алғашқы симплекс - кесте құрылады (№1-симплекс кестесі) . Кестеде жолға әр тік графаларға негізгі айнымалылардың белгілері және соңғы (немесе 2-шІ) тік графаға босмүшелердің белгісі жазылады. Сонымен қатар, бірінші жолдың сол жағындағы бірінші торда белгісімен әр "Итерация"-ның симплекс кестесінің реттік нөмірі көрсетіледі. бағанаға әр жатық графаларға базис тік айнымалылардың белгілері, ал ақырғы жатық графағамақсат функцияның белгісі жазылады. Кесте айнымалылардің коэффициенттермен, босмүшелермен толтырылады, яғни өздерінің орындарына сәйкес торларға жазылады. Симплекс кестесінің соңғы жолын индекстік немесе мақсат функцияның жолы деп атайды.
1 - кесте
Y 1
Y 2
…
Y m
a 11
a 21
…
a m1
a 12
a 22
…
a m2
…
…
…
…
a 1k
a 2k
…
a mk
a 1k+1
a 2k+1
…
a nk+1
…
…
…
…
a 1n
a 2n
…
a nm
b 1
b 2
…
b m
Бұл кестені математика тілінде матрица деп те атайды, ал 1-ші тік графада тұрған сандарды матрицаның 1-ші бағанасының элементтері, 2-ші тік графада тұрған сандарды матрицаның 2-ші бағанасының элементтері және т. б. с. с. ал 2-ші жатық графада тұрған сандарды матрицаның 1-ші жолының элементтері дейді жәнет. б. с. с.
Есепті шешуді симплекс кестені талдаудан бастайды, яғни шешуші бағананы шешуші жолды және шешуші элементті анықтайды. Әдебиеттерді бұл көрсеткіштерді әр түрлі атайды (бағыттаушы немесе кілттік бағана, бағыттаушы немесе кілттік жол және генералдық немесе бас элемент) Бұл көрсеткіштерді бағыттаушы бағана, бағыттаушы жол және бас элемент деп атайық. Симплекс кестені талдау бағыттаушы бағананы анықтаудан басталады. Есепті шешу мынадай алгоритм бойынша жүргізіледі:
1. m+1 жолдың теріс таңбалы элементтері ішінен абсолюттік шамасы ең үлкені таңдайды:
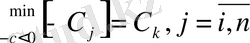
Осы бағана бағыттаушы бағана деп аталады да к-мен белгіленеді. Бағыттаушы бағана табудағы мақсат, негізгі белгісіздердің ішіндегібазиске енетінін анықтау. Олай болса, Хк базистік белгісіздердің қатарына енетіні. Геометриялық заңы бойынша базистың саны берілген теңдеу саны керек, ендеше базистік белгісіздердің бірі базистық құрамына шығып Хк-нің орнына бару керек, былайша айтқанда олар өзара орны ауыстырады. Орын ауыстырудан бұрын базистік белгісіздердің құрамынан шығатын белгісізді анықтайық.
2. Бос мүшелер бағанасындағы (Ьі) базистік белгісіздердің жолында жатқан әр санды бағыттауыш бағанасында (к) орналасқан элементтерге бөледі де ішіндегі ең кіші бөліндіні (міндетті түрде бөлінді әрқашанда оң сан болу керек) анықтайды, яғни:
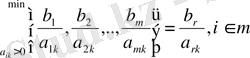
демек ең кіші қатынас r-ші жатық жолда жатыр екен делік, онда г-ші жатық жолда бағыттауыш жол деп атайды. Бағыттауыш бағанамен бағыттауыш жолдың қиылысуында жатқан элемттті (әдебиеттерде әр түрлі аталады: генералды немесе бас, немесе шешуші, немесе бағыттаушы) бас элемент деп атайды да а rk мен белгілейді. Бағыттаушы жатық жолдың нөмірі r -мен белгіленеді де, У j - базистік белгісіз базистан шығарылатыны анықталынады.
3. Енді Х к мен У r - дің орындарын ауыстырып, жаңа кесте тұрғызу жолын қарастырайық, яғни бір базистен екінші базиске (бір кестеден бағаналары бар) және жатық жолдары бар жаңа матрица құруымыз керек. Мұндағы негізгі матрицаны А деп белгілесек (соңғы бағана және соңғы жатық жолдың элементтері негізгі матрицаға ен-бейді), онда А матрицасының өлшемі болады, былайша айтқанда А матрицасы элеменгтен тұрады. Ал егер А матрицасына соңғы бос мушелер бағанасын b 1 , b 2 , …, b m қоссақ, ондағы шыққан матрицаны кеңейтілген матрица дейді де, А 1 арқылы белгілейді. Осы матрица жөніндегі түсініктен кейін 1-кестені пайдаланып, бір базистен (бір төбеден екінші төбеге көшу) екінші базисқа көшу жолын қарас-тыралық. Ол үшін ең алдымен шешімнің оптималды шартына түсі-ніктеме берейік, яғни былайша айтқанда оптималды төбеге жеткенімізді қалай білеміз?
Сызықты программалау есебінің оптималдық шарты жөнінде мынадай теорема белгілі: егер мына жағдайда
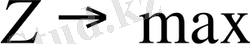 табылған шешімде мақсат функцияның коэффициенттері С
j
, яғни соңғы m+1 жатық жолдың (босмүшелер бағанасындағы элементті қоспағанда) барлық элементтері оң болса (мына жағдайда
табылған шешімде мақсат функцияның коэффициенттері С
j
, яғни соңғы m+1 жатық жолдың (босмүшелер бағанасындағы элементті қоспағанда) барлық элементтері оң болса (мына жағдайда
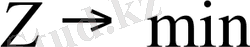 , керісінше барлық элементтер теріс болуға тиіс), онда осы шешім оптималды делінеді.
(Ескерту:
Бұл теореманың математикалық дәлелденуі тәжірибелік есептер шығару барысында өзінен-өзі түсінікті болады) .
, керісінше барлық элементтер теріс болуға тиіс), онда осы шешім оптималды делінеді.
(Ескерту:
Бұл теореманың математикалық дәлелденуі тәжірибелік есептер шығару барысында өзінен-өзі түсінікті болады) .
Жоғарыдағы теоремада берілген оптималды шешімнің шарты бойынша шешім оптималды шешімді бермейді, себебі мақсат функцияның коэффициенттерінің барлығы теріс таңбалы сандар.
Симплекс әдісінің негізгі мақсаты бастапқы шешімді (жоспарды) бірте-бірте жақсарта отырып, ең пайдалы (оптималды) жоспарға жету. Х к мен У r -дің орныи ауыстыру жұмысы берілген теңдеулердің ішінен r-ші теңдеуді тауып, оны Х к бойынша шешіп, табылған Х k -ның мәнін қалған теңдеулерге енгізу, яғни жүйенің r-ші теңдеуі былай жазылады:
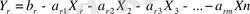
Осы теңдеуден Х к -ны тапсақ:
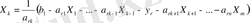
Енді бұл Х - тың (6) жүйедегі қалған теңдеулерге қойсақ
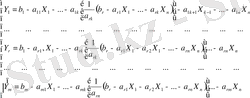
Бұл теңдеулердегі жақшаны ашып, Х - тердің сәйкес клэффиценттерін топтап жазсақ, жалпы түрде былай болар еді:
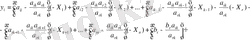
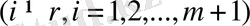
Жақша ішіндегі коэффиценттерге сәйкес a ij және b 1 деп белгілесек теңдеу мына түрге келеді:
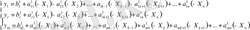
Демек, жаңа кесте элементтері
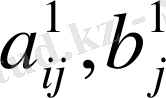 және
және
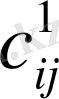 табу үшін Х
к
- нің мәнін мақсат функциясындағы Х
к
- ның орнына қойсақ:
табу үшін Х
к
- нің мәнін мақсат функциясындағы Х
к
- ның орнына қойсақ:
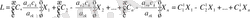
болады (мұнда Х к - ның орындау у r жазылады) .
Бұдан біз матрицаның (кестенің) жаңа элементтері қалай табылатынын аңғардық, яғни оларды мынадай формулалармен есептеуге болады.
- Бас элементінің орнындағы жаңа элемент:
(осы формуламен табылған бас элементтің жаңа мәнін жаңа кестеге бас элемент тұрған жерге жазамыз) .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz