Сызықтық емес программалау: теориясы, шешу әдістері және өндірістік-экономикалық қолданбалары


-Мазмұны.
Кіріспе . . .
І бөлім. Сызықтық емес программалау есебі.
- Сызықтық емес программалау есебінің жалпы қойылуы. .
- Мақсат функция сызықты емес және шектеулер жүйелері сызықты СЕП есебі . . .
ІІ бөлім. Сызықтық емес программалау есебін шешудің қосалқы әдістері .
2. 1. Мақсат функциясы сызықты емес және шектеулер жүйесінде теңсіздіктеріде сызықты емес СЕП есебінің берілуі . . .
2. 2. Логранж көбейткіштер әдісі . . .
Қорытынды . . .
Қосымша
Пайдаланылған әдебиеттер . . .
Кіріспе.
Сызықты емес программалау (СЕП) есептерінің сипаты және дәрежелері сызықты программалау есептеріне қарағанда кеңірек және жоғары.
СЕП есептері тауар қорларын басқаруда, құрал жабдықтарды жөндеу жұмыстарын ұйымдастырғанда, халық шаруашлығы кәсіпорындарының өндірістеріне болжаулар жасағанда және т. б. халық шаруашылық есептерінде қолданылады.
СЕП есептерінің СП есептерінен айырмашылығы, олардың бәріне бірдей шешу әдістері жоқ және шешімі бола алатын аймақ (ШМБА) барлық уақытта дөңес бола бермейді. Кейбір есептерде ШМБА дөңес болған кездің өзінде мақсат функцияның бірнеше локальды экстремалды мәндері болуы мүмкін. Мұндай кезде әр түрлі есептеу әдістерімен локальды экытремалды мәндердіберетін нүктелерді табуға болады, бірақ осы мәндердің ішінен глобальды (обсалюттік ең төменгі немесе ең жоғарғы) эксрималдық мәнді анықтау ең қиын іс және ірден оны анықтау мүмкін емес. Мақсат функцияның және шектеулер жүйелерінің түрінде байланысты СЕП есептерін шешу үшін бірншеше арнайы әдістер дасалған. Оларға Лангранж әдісі, графиктік әлістері және жуықталған әдістер жатады.
Егер СП есебінің экстрималды нүктесі көпжақтылардың төбелерінде болса, ал СЕП есептерінің экстрималды нүктелері көбжақтылардың төбелерінде немесе қабырғаларында, немесе қырында, немесе осы дененің ішінде жатуы мүмкін.
Курстық жобаның мақсаты: Сызықтық емес программалау әдістерін пайдаланып, халық шаруашылығында күнделікті қолданылатын өндіріс орындарын жоспарлау, өнідірістен мүмкін болғанша жоғары өнім алу, техниканы өндіріс құралдарын дұрыс пайдалану, малға тиімді рацион жасау, қатынас есептерін шешу, халық шаруашылығын өркендету мәселелері қарастыратын есептер шығару.
Зерттеу міндеттері:
1. Тәжірибелік есептерді шығару кезеңдері.
2. Сызықты емес теңсіздіктермен жұмыс.
3. СЕПЕ математикалық модельдерінің жазылуы.
4. Бір түрден екінші түрге өту кезеңдері.
5. Жүйедегі шектеулердің бірлесуі.
Зерттеу объектісі: Сызықтық емес программалау есебінің қойылуы, формалдау, математикалық моделін құру, әдісті таңдап алу, берілген әдіске бағдарлама құру, тәжірибеде қолдану.
Зерттеу пәні: Өндірістік және экономикалық процестерді модельдеу
Зерттеу әдістері: Журналдар, сызба суреттер, программалық көірінстер, проектор.
Курстық жобаның құрылымы: Кіріспеден, екі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.
І бөлім. Сызықтық емес программалау есебі.
1. 1. Сызықтық емес программалау есебінің жалпы қойылуы.
Жалпы математикалық программалау есептерінің математикалық моделінің жазылу жолы бір типтес. Мысалы, мына шектеулер жүйелерін қанағаттандыратын
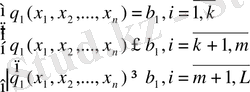 және
және
 (сонымен қатар
(сонымен қатар
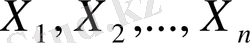 - бүтін сандар болуы мүмкін ) мына функцияны
- бүтін сандар болуы мүмкін ) мына функцияны
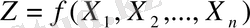
экстремалды және жеткізетін
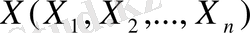 - векторын табу керек деп жазылатыны белгілі.
- векторын табу керек деп жазылатыны белгілі.
Көрсетілген жағдайларды қанағаттандырмайтын кез келген математикалық программалау есептері сызықты емес программалау есебі деп аталады.
Сызықты емес программалау (СЕП) есептерінің сипаты және дәрежелері сызықты программалау есептеріне қарағанда кеңірек және жоғары.
СЕП есептері тауар қорларын басқаруда, құрал жабдықтарды жөндеу жұмыстарын ұйымдастырғанда, халық шаруашлығы кәсіпорындарының өндірістеріне болжаулар жасағанда және т. б. халық шаруашылық есептерінде қолданылады.
Жалпы СЕП есептерінің мәнісі функцияның
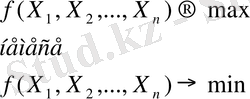
максималды немесе минималды мәнін анықтауда.
Сонымен қатар, егер Z - функциясы n-функциялардың (∑) қосындысы болса, онда
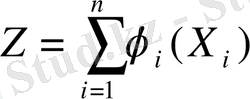
Оны «Сеперабельді» немесе егер Х
і
- ң біреуі екінші (шаршы) дәрежелі болса, онда оны шаршыланған (квадратическая) деп атайды. Екң жағдайа да мақсат функцияның экстремалдық мәні мына шарттарда:
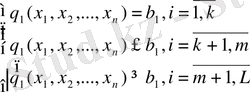
және

ізделінеді.
СЕП есептерінің СП есептерінен айырмашылығы, олардың бәріне бірдей шешу әдістері жоқ және шешімі бола алатын аймақ (ШМБА) барлық уақытта дөңес бола бермейді. Кейбір есептерде ШМБА дөңес болған кездің өзінде мақсат функцияның бірнеше локальды экстремалды мәндері болуы мүмкін. Мұндай кезде әр түрлі есептеу әдістерімен локальды экытремалды мәндердіберетін нүктелерді табуға болады, бірақ осы мәндердің ішінен глобальды (обсалюттік ең төменгі немесе ең жоғарғы) эксрималдық мәнді анықтау ең қиын іс және ірден оны анықтау мүмкін емес. Мақсат функцияның және шектеулер жүйелерінің түрінде байланысты СЕП есептерін шешу үшін бірншеше арнайы әдістер дасалған. Оларға Лангранж әдісі, графиктік әлістері және жуықталған әдістер жатады.
Егер СП есебінің экстрималды нүктесі көпжақтылардың төбелерінде болса, ал СЕП есептерінің экстрималды нүктелері көбжақтылардың төбелерінде немесе қабырғаларында, немесе қырында, немесе осы дененің ішінде жатуы мүмкін.
Егер СЕП есебі сызықсыз шектеулер болса, онда шешім бола алатын аймақ дөңес болмайды және глобалдық оптимумнан (ең кіші немесе төмен емес) болуы мүмкін.
СЕП есебі шешу алгоритмін нақтылы тұжырымдау үшін бірнеше мысалдар мен тәсілдерді қарастырамыз.
Есептің графикалық әдісі.
Сеп есебін графикалық жолмен шешу мынадай кезеңдерден тұрады:
1.
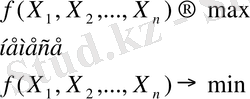 қатынаспен анықталған есептің шешімі мүмкін бола алатын аймақты табады (егер ол бос болса, онда есептің шешімі жоқ) .
қатынаспен анықталған есептің шешімі мүмкін бола алатын аймақты табады (егер ол бос болса, онда есептің шешімі жоқ) .
2.
 -гипержазықтығы құралады.
-гипержазықтығы құралады.
3. Гипержазықтықтың ең биік (ең төменгі) деңгейі анықталынады немесе есептің көптік шешімі бола алатын аймаққа мақсат функцияың шешулеріне байланысты шешімі жоқ екендігі анықталады.
4. Гипержазықтықтың ең биік (ең төменгі) деңгейі өтетін шешімі мүмкін болаалатын аймақтан бір нүкте табылады және сол нүкте функция
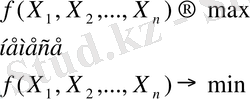 мәнін анықтайды.
мәнін анықтайды.
Мысал.
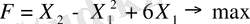
мына жағдайда:
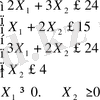
Координат өсінде жүйедегі теңсіздіктердің графиктерін тұрғызайқ. Берілген есептің шешімі мүмкін бола алатын аймақ ОАВС көпбұрышы (1-сурет) . Осы аймақтан Функция максималды мәнге жететін нүктені анықтаиды. Ол үшін деңгеи сызықты
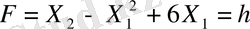
тұрғызамыз. Мұндағы h - кез келген тұрақты шама, осы көрсеткіштің әртүрлі мәнінде функция қалай өзгеретінін зерттейік. h - ң әр мәнінде парабола аламыз. Ол ОХ осіне қашықтаған сайын h - мәні өседі. ОАВС қырының бірінде парабола жанасқан жерінде функция максималды мәніне жетеді.
Есепте парабола
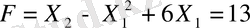
1 - сурет.
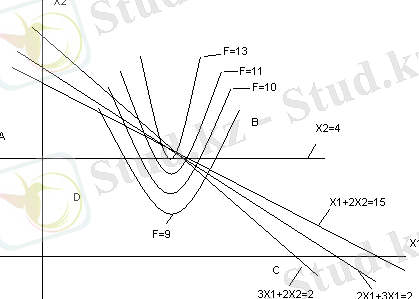
АВ қабырғасымен D нүктесінде жанасады. Бұл нүктенің координатын мына теңдеулер жүйесін шешу арқылы табуға болады.
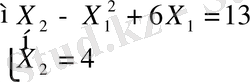
Жүйеден мына мәндерді таптық:
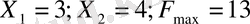
Сонымен есепті шығарудың нәтижесінде мақсат функцияның максималды мәні көпбұрыштың төбесінде емес екеніне көзіміз жетті. Сондықтан сызықты программалау есебінің геометриялық шығару жолын, яғни көббұрыштың барлық төбелерін қарап шығу тәсілін бұл есепке қолдануға болмайды.
Мысал:
Мақсат фукнцияның
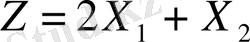
мына жағдайда:
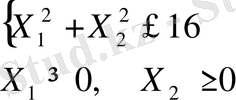
глобалдық (обсалюттік) экстремалды мәнін табу керек.
Шешімі: шешімі мүмкін бола алатын аймақ радиюсы 4 - ке тең шеңбердің төрттен бір бөлігі, ол координаттар өсінің бірінше ширегінде орналасқан (2 - суретті қараңыз) .
Деңгей сызығы (
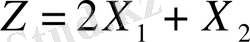 ) өз - өзіне паралельді жылжытып отырып, шеңбермен жанасу нүктесіне дейін апарамыз. Сүретте деңгей сызығы шеңбермен А нүктесінде жанасқан. Деңгей сызығының (Х
2
=-2Х
1
) бұрыштық коэффиценті - 2 ге тең. Функция глобалдық минимумына О(0. 0) нүктесінде ал глобалдық максимум оның шеңбермен жанасу нүктесінде жетеді.
) өз - өзіне паралельді жылжытып отырып, шеңбермен жанасу нүктесіне дейін апарамыз. Сүретте деңгей сызығы шеңбермен А нүктесінде жанасқан. Деңгей сызығының (Х
2
=-2Х
1
) бұрыштық коэффиценті - 2 ге тең. Функция глобалдық минимумына О(0. 0) нүктесінде ал глобалдық максимум оның шеңбермен жанасу нүктесінде жетеді.
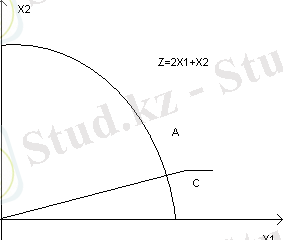
2 - сурет
А нктесі арқылы деңгей сызығына перпендикуляр жүргіземіз. Бұл тік бұрыш сызық координаттың бас нүктесі арқылы өтеді және оның бұрыштық коэффиценті
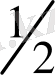 тең, сонымен қатар ол мынадай теңдікпен өрнектеледі:
тең, сонымен қатар ол мынадай теңдікпен өрнектеледі:
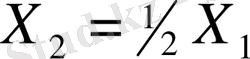
Нәтижесінде мынадай теңдіктер жүйесі табылады:
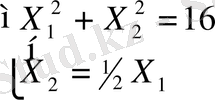
Жүйені шешу нәтижесі:
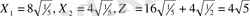
Сөйтіп глобалды максимум мақсат функция
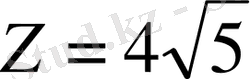 , ал сол нүктенің кординаты
, ал сол нүктенің кординаты
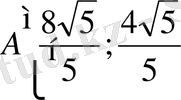
1. 2. Мақсат функция сызықты емес және шектеулер жүйелері сызықты СЕП есебі
Мысал.
Мына функцияның
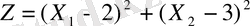
мына жағдайда:
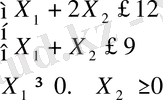
глобалдық экстремалды мәнін табу керек.
Шешімі: Координаттар өсінде жүйедегі шектеулерді пайдаланып олардың графигін тұрғызамыз (3 - сурет)
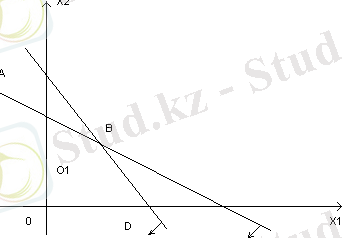
3 - сурет.
Берілген Z - мақсат функциясы формуласы бойынша шеңбер құруға болады. Шеңбердің бас нүктесін (0 1 ) координаттары осы теңдік арқылы табылады, ол О 1 (2; 3) .
Сонымен Z - мақсат функциясы минималды мәнінде, О 1 - нүктесінде, ал максималды мәнінде D - нүктесінде жетеді. D - нүктесінің координаты D(9; 0) .
Z - функциясының ең үлкен (глобалдық) максималды мәні:
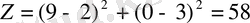
D - нүктенің координаттары сәйкес. Ал Функцияның ең кіші (глобалдық) минималды мәні:
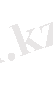
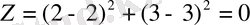
О 1 - нүктенің координаттарына сәйкес.
Тағы бір есепті қарастырайық.
Мысал: мына функцияның
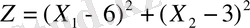
мына жағдайда
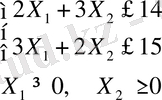
Глобалдық экстрималды (ең үлкен және ең кіші) мәндерін іздейік.
Шешімі: Координаттар өсінде жүйедегі етңсіздіктердің графиктерін тұрғызайық. Шешімі мүмкін бола алатын аймақ - ОАВD.
Деңгей сызығы, бас нүктесі О
1
(6. 3) шеңбер түрінде бейнеленеді. Ең үлкен максималды мән О(0. 0) нүктесіне сәйкес келеді. Өйткені, ол шеңбердің бас нүктесінен ең алыс орналасқан шешімі мүмкін бола алатын аймақтың ең шеткі нүктесі. Ең кіші минималды мән Е - нүктесінің координаттарына сәйкес. Ол нүкте
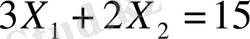 түзу сызығына О
1
- нүктесінентік бұрышпен түсірілген сызықтың қиылысында жатыр.
түзу сызығына О
1
- нүктесінентік бұрышпен түсірілген сызықтың қиылысында жатыр.
Енді осы Е - нүктесіунің координаттарын іздейік.
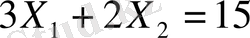 сызығының бұрыштық коэффиценті -
сызығының бұрыштық коэффиценті -
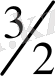 тең, ал оған тік бұрышпен түсірілген сызық О
1
Е-ң бұрыштық коэффиценті
тең, ал оған тік бұрышпен түсірілген сызық О
1
Е-ң бұрыштық коэффиценті
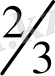 тең. Олай болса, бұрыштық коэффиценті
тең. Олай болса, бұрыштық коэффиценті
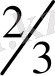 тең. О
1
-нүктесінен өтетін түзу сызықтың түрі
тең. О
1
-нүктесінен өтетін түзу сызықтың түрі
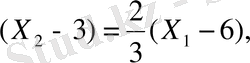 бұдан
бұдан
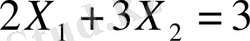
Нәтижесінде
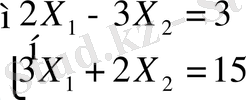
жүйеден Е - нүктенің кооринаттарын табамыз.
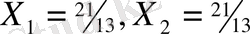
демек
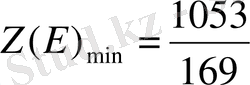
Е - нүктесінің координаттарын басқаша да есептеуге болады. X 1 - і анықталмаған функция деп есептеп
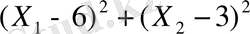
өрнегінен туынды алып, мына өрнекті табамыз.
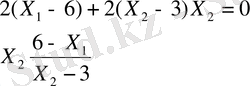
Алынған мәнді
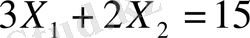 түзудің қисық бұрышының тангенсіне теңесіп мынаны аламыз:
түзудің қисық бұрышының тангенсіне теңесіп мынаны аламыз:
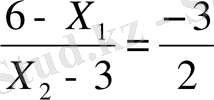
немесе
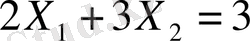
нәтижесінде
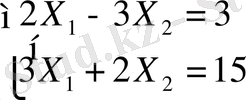
Жүйелен Е - нүктесінің координаттарын анықтаймыз.
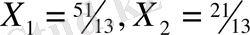
ІІ бөлім. Сызықтық емес программалау есебін шешудің қосалқы әдістері .
2. 1. Мақсат функциясы сызықты емес және шектеулер жүйесінде теңсіздіктеріде сызықты емес СЕП есебінің берілуі
Мысал: Функцияның

мына жағдайда
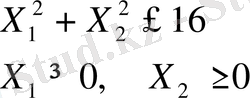
экстремалдық мәнін анықтайды.
Шешімі: Шектеудегі теңсіздік
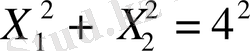 - радиюсы 4 - ке тең шеңберді өрнектейді Сондықтан, координаттаржүйесіне ШМБА 1-ширекте жатқан осы шеңбер жазықтығының төрттен бір бөлігі. Деңгей сызығыда шеңбер түрінде өрнектеледі, оның бас нүктесінің координаты О
1
(2; 1) (5 - сурет) .
- радиюсы 4 - ке тең шеңберді өрнектейді Сондықтан, координаттаржүйесіне ШМБА 1-ширекте жатқан осы шеңбер жазықтығының төрттен бір бөлігі. Деңгей сызығыда шеңбер түрінде өрнектеледі, оның бас нүктесінің координаты О
1
(2; 1) (5 - сурет) .
Функцяның ең кіші мәні О 1 - нүктеде жатыр, ал максималды мәніне А(0; 4) нүктеде жетеді. Олай болса
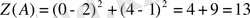
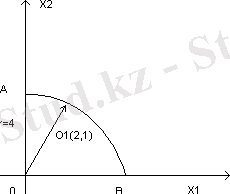
5 - сурет.
Мысал: Мына функцияның
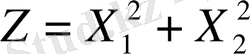
мына жағдайда:
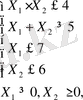
ең үлкен және ең кіші мәндерін табайық.
Шешімі: ШМБА - дөңес емес және ол екі бөлімнен тұрады (6-сурет) . Деңгей сызығы, бас нүктесі О(0. 0) болатын шеңбер сызығы. А жән В нүктелердің координаттарын табайық, ол үшін:
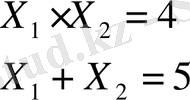
Нәтижесінде А(1; 4), В(4; 1) . Бұл нүктелерде Z - фуекциясы:

Ең кіші мәніне жетеді.
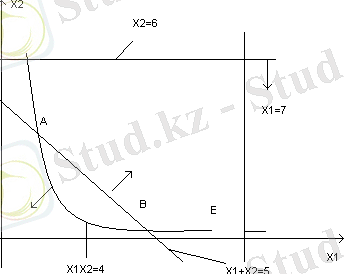
6 - сурет.
Мына жүйелермен D және Е нүктеғлердің координаттары
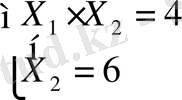
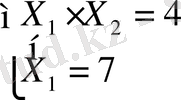
D(
 Equation. 3 ), онда Z(D) =
Equation. 3 ), онда Z(D) =
 Equation. 3 және Е(7;
Equation. 3 және Е(7;
 ), онда
), онда
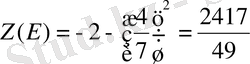
болатыны анықталады.
Сонымен мақсат функция Z, Е(7;
 ), нүктесінде өзінің ең үлкен мәніне жететіні байқадық.
), нүктесінде өзінің ең үлкен мәніне жететіні байқадық.
2. 2. Логранж көбейткіштер әдісі.
Айталық мына шектеуде
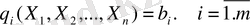
Мынадай функциның экстрималдық мәні ізделінсін.
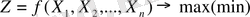
Шектеулер теңдеу түрінде белгіленгендіктен оларды шешу үшін, бірнеше айнымалылардан тұратын функцияның экстрималдық мәнін іздейтін белгілі классикалық әдістіә қолдануға болады. Бұл кезде
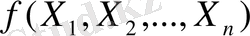
және
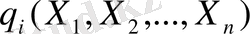
функциялар өздерінің жекешеленген туындыларымен бірге үздіксіз деп есептелінеді.
Есептің шешімін табу үшін қосымша
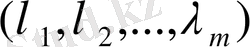 айнымалылары енгізіледі. Нәтижесінде Логранж Функциясы құрылады.
айнымалылары енгізіледі. Нәтижесінде Логранж Функциясы құрылады.
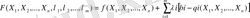
Функциядан жекелеген туындылар алынады: Х і бойынша
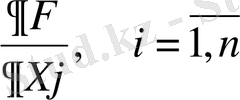
және
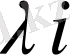 бойынша
бойынша
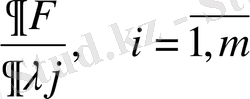
Қорытындысында (n+m) - нен тұратын теңдецулер жүйесі тұрғызылады.
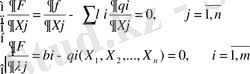
Осы жүйені шешу нәтижесінде
 - табылады.
- табылады.
Сонымен СЕП есебін Логранж көбейткіші арқылы шығару жұмысы мынадай кезеңдерден тұрады:
- Логранж функицясықұралы.
- Логранж функциясынан Хj және λj бойынша жекелеген туынды алынады да, теңдеулерді нөлге теңестіреді.
- Тұрғызылған теңдеулер жүйесін шешу арқылы, мақсат функциясы экстремалды мәніне жететін нүктелерді табады.
Теңдеулер жүйесінің бірншее шешімдері болуына байланысты
Логранж әдісін қолдан шектеулі.
Мысал:
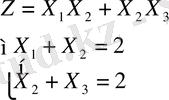
Шешуі: логранж функцясын тұрғызамыз:
 Хj және λj бойынша жекелеген туынды алынып, теңдікті нөлге теңестіріп жазып, мынадай теңдіктер жүйесін аламыз.
Хj және λj бойынша жекелеген туынды алынып, теңдікті нөлге теңестіріп жазып, мынадай теңдіктер жүйесін аламыз.
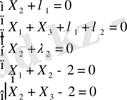
Бірінші және үшінші теңдеуден:
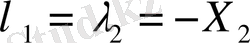
Олай болса
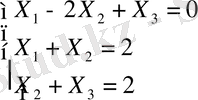
Осы жүйені шешу нәтижесінде:
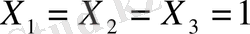 және Z=2 алдық.
және Z=2 алдық.
Есеп. Кәсіпорындар 180 бұйым дайындамақшы. Бұл бұйымдар екі түрлі техналогиялық тәсілмен, әр түрлі шығынмен дайындалуы мүмкін. Егер Х 1 - бұйым 1 - тәсілмен жасалатын болса, онда шығын мына заңдылықпен өзгереді.
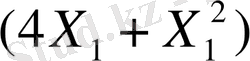
теңге, ал Х 2 бұйым екі тәсілмен жасалынса, онда шығын:
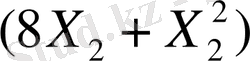 теңге.
теңге.
Жалпы өндірістік шығын аз болу үшін әр техналогиялық тәсілмен қанша бұйым шығарған тиімді болатын анықтау керек.
Шешімі: Есептің мақсаты:
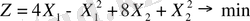
мына жағдайда:
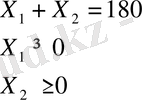
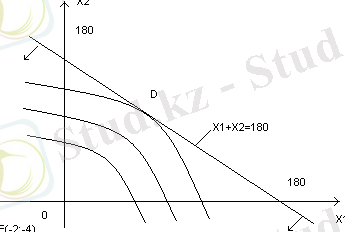
7- сурет.
Есепті геометриялық тәсілмен шығарайық. Координаттар өсінде есептің шешімі мүмкін бола алатын аймақ. АВ кесіндісімен шектелген. Днңгей сызығы шеңбер арқылы бейнелейді. Шеңбердің бас нүктесінің (Е) координаттарын табу үшін мақсат функциясының өрнегін нөлге теңестіреміз.
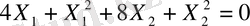
Айталық, Х 1 =0, онда
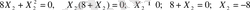
Егер Х
2
=0 десек, онда
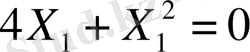 ; Х
1
=-4 немесе
; Х
1
=-4 немесе
Х 1 =-2 және Х 2 =-4. Демек Е(-2; -4), яғни деңгей сызығы бас нүктесі осы нүктеге сәйкес келетін шеңбер арқылы бейнеленеді.
Осы бас нүктеден радиюсы әр түрлі ұзындыққа шеңбер жүргізсек, мақсат функцияның минималды мәні шеңбердің АВ кесіндісімен жанасу D-нүктесінде екеніне көз жеткізуге болады.
Енді D-нүктесінің координаттарын табу үшін, шеңбердің осы нүктеде бұрыштық коэффицентімен және Х 1 +Х 2 =180 сызығының бұрыштық коэффиценті дәл келетінін ескеріп, мынадай есептеулер жүргіземіз.
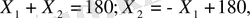 бұдан k=-1
бұдан k=-1
Мақсат функциясы Х
1
бойынша дифференциалдап және оны Х
2
бойынша айқындалмаған функциясы етінде қарап, мына түрде жазуға болады:
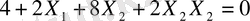 немесе
немесе
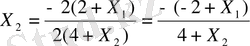
мұндағы Х 2 - шеңбердің бұрыштық коэффицентінде тең екені белгілі, олай болса
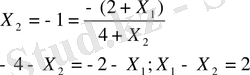
Осы әрекеттен киін D - нүктесі үшін теңдеулер жүйесін құрамыз:
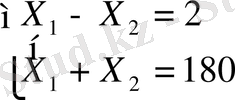
Жүйеден
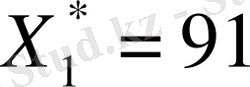 және
және
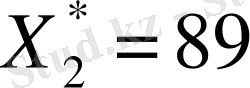 таптық. Сөйтіп, кәсіпорын 1-техналогиялық тәсілмен 91 бұйым, 2- техналогиялық тәсілмен 89 бұйым жасаса, жалпы шығын:
таптық. Сөйтіп, кәсіпорын 1-техналогиялық тәсілмен 91 бұйым, 2- техналогиялық тәсілмен 89 бұйым жасаса, жалпы шығын:
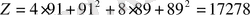
теңгеден аспайды.
Енді есепті Логранж көбейткіштері арқылы шығарайық.
Логранж функциясын тұрғызамыз:
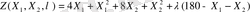
Жекелеген туындыларды тауып, алынған теңдеулерді нөлге теңестіріп, нәтиесінже мынадай теңдеулер жүйесін құрамыз.
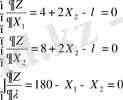
Осы жүйені шешу нәтижесінде
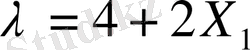 ;
;
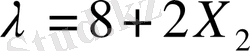 немесе
немесе
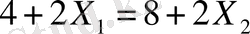 немесе
немесе
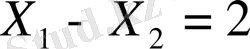 жаңа жүйені тұрғызамыз.
жаңа жүйені тұрғызамыз.
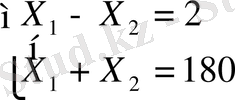
бұдан
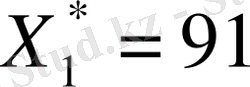 және
және
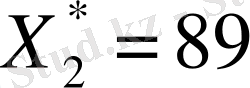 .
.
Жоғарыдағы жағдайды тағы да қайталадық және осы нүктелерде мақсат функциясы минималды мәніне жететіндігіне көзіміз жетті.
Тағы бір мысал қарастырайық.
Мысал:
берілген функцияның
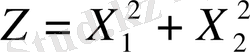 - экстремалды мәнін мына жағдайда: Х
1
+Х
2
=5 іздейік.
- экстремалды мәнін мына жағдайда: Х
1
+Х
2
=5 іздейік.
Шешімі: Логранж функциясын құрастырайық.
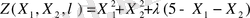
Оның жекелеген туындысын табайық та, теңдеулерді нөлге теңестірейік, нәтижесінде:
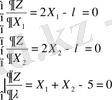
Бірінші және екінші теңдіктерден Х
1
-Х
2
=0 таптық. Осы теңдік жүйедегі үшінші теңдікті бірге шешу нәтижесінде:
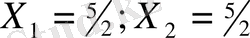 алдық. Сонымен
алдық. Сонымен
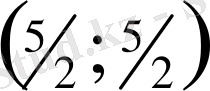 нүктелерінде функция (Z) өзінің экстриамлдық мәніне жеткенін дәлелдеу үшін қосымша зерттеулер жүргізуге тура келеді. Ол үшін екінші жеке туындыны тауып, осы нүктелерден функция (Z) шарты минималды мәніне жететінін көрсетуге болады және ол тең:
нүктелерінде функция (Z) өзінің экстриамлдық мәніне жеткенін дәлелдеу үшін қосымша зерттеулер жүргізуге тура келеді. Ол үшін екінші жеке туындыны тауып, осы нүктелерден функция (Z) шарты минималды мәніне жететінін көрсетуге болады және ол тең:
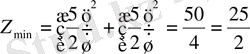
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz