Барлық денелер бір-біріне тартылады

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

ТАРТЫЛЫС КҮШТЕРІ

Барлық денелер бір-біріне тартылады. Денелердің Жерге құлап түсуі, тұйықталған орбита бойымен Айдың Жерді айналуы, планеталардың Күнді айнала қозғалуы сияқты құбылыстар бүкіл әлемдік тартылыс күштерінің ықпалынан болады. Тартылыс күштері бағынатын заңды ен, алғаш, 1687 жылы Ньютон тұжырымдап айтқан. Ньютонның бүкіл әлемдік тартылыс заңы бойынша: әрбір екі дене біріне-бірі, өздерінің массаларының көбейтіндісіне тура пропорционал, ара қашықтығының квадратына кері пропорционал күшпен тартылады. Біріне-бірі тартылатын денелердің массаларын т ₂ және т ₂ әріптерімен, олардың ара қашықтығын r әрпімен белгілесек, мына фор-мула шығады:

(1)

мұндағы k- белгілі тұрақты шама, бұл тартылыс тұрақтысы деп аталады; оның сан мәні күштің, массаның және ара қа шықтықтын қандай бірліктермен өлшенгеніне байланысты болады.

Ньютонның заңы жоғарыда ай-^тылған түрінде, тек денелердің өл-шемдері олардың г ара кашықтығы-мен салыстырғанда кішкене болса ғана дүрыс болады. Егер денелердің өлшемдері олар-дың ара қашықтығымен шамалас болса, онда денелердің әрқайсысын кішкене элементтерге бөлген жен (68-сурет), солай еткенде әрбір екі элемент үшін Ньютонның тартылыс заңы дүрыс болады, сон-да бірінші дененің Мнші элементі мен екінші дененің i -іншы элементінің өз ара әсер етуші күші мынаған тең болады:

Формасы әр түрлі денелер үшін осылайша есептеудің нәтижесі сан алуан болып келеді; біртекті шарлар тартылысы жағдайын-да бүл айрықша жеңіл болады: біртекті екі шардың бір-біріне

тартылыс күші [ = к -^, мұндағы пі\ және /п ₂ - шарлардын.

массалары, г - олардың центрлерінің ара қашықтығы. Бұл тең-дік (1) формулаға дәл келеді және шарлардың ара кашықтығы кандай болса да дүрыс болады.

XVIII және XIX ғасырлар бойы кептеген физиктер жалпы әлемдік тартылыс туралы теріс, идеалистік кезқараста болды, олар тартылысты аралықтағы кеңістіктің ешбір қатысы жоқ, «алыстан әсер ету» деп қарады.

Шы?ідығында дене езін қоршаған кеңістікте өзгерістер туғы-зады, материяның ерекше түрі болып табылатын тартылыс өрісі пайда болады (кітаптың II томында электромагниттік өріс тура-лы айтылатынмен салыстырыңыз) . Денелердін, тартылыс ерісте-рімен өз ара әсер етуінен барып, денелер біріне-бірі тартылады.

Бүкіл әлемдік тартылыс заңы бойынша Жер бетінде барлық дене бірдей үдеумен төмен түсуге тиіс. Дұрысында, дененің мас-сасы т болса, ол мынадай үдеу алады:

т '

мұндағы / - денені Жер шарына қарай тартатын күш. Ньютон-ның тартылыс заны бойынша:

, _ . тМ _ж

«V Ж

Жер шарының радиусы,

мүндағы М _ж - Жердің массасы, /? сонда

. т ■ М _ж 1, М^

Жердің массасы мен оның радиусы тұрақты шамалар, сондық-тан Жер бетінде барлық дене, олардың массаларының қандай екендігіне қарамай, бірдей үдеумен төмен түседі, ол үдеу

Мұнда, әрине, сәз денелердің еркін түсуі туралы, яғни кедергі күштері жоқ, оның ішінде ауа кедергісі де жоқ жағдайда төмен түсу туралы болып отыр. Мұнда ауырлық күшінің географиялық ендікке тәуелділігі де есепке алынбайды (23-параграфты қараң-дар) .

Массасы т кез келген дененің Жерге қарай тартылатын күші сол дененің Жер бетінен қандай биіктікте (һ) тұрғандығына байланысты болады. Нью-тонның тартылыс заны бойынша дене Жерге карай мынадай күшпен тарты-лады:

, _ тМ _ж / - й ^ ₂ і

мұндағы К -Жер центрінен денеге дейінгі қашықтық, бұл Н=Нж+һ бол-ғандықтан

Осы I куші дененің һ биіктіктегі салмағы {Яһ) болып табылады; Жердің дәл бетіндегі оның салмағын Р _о әрпімен белгілесек, сонда:

тМ _ж

Ро

бұдан

іс жүзінде һ әркашан Жердің Р _ж радиусымен салыстырғанда ете аз шама болады, сондықтан жуыктап алғанда

Л>

Жер шарынык радиусы тау төбесінде:

Рн

1 + 2 _Г

6370 км болса, осыдан биіктігі 6, 4 км биік 2

= 1-2

1 -

1000

Ро

= 1-0, 002,

іс жүзінде һ әрқашанда салмағының оның теңіз деңгейіндегі салмағынан айырмашылығы тек 0, 2% қана болады. Тартылыс күшінің қашықтыққа тәу-елді екендігін дененің Жер бетіндегі салмағын бақылай отырып тағайындауға болады, бірақ бұл тәуелділік өте аз, сондықтан ол тартылыс күшінің дене-лердіц ара қашықтығының квадратына кері пропорционал екендігін дәл тек-серуге жарамайды. Ньютон тартылыс күшініқ денелердің ара қашықтығынын квадратына кері пропорционал екендігін, Айдың козғалысын қарастыра келіп тағайындаған. Ньготон былай ойлаған: егер тартылыс заңын (1) фор_муламен өрнектеу дұрыс болса, Жердің Айды тартатын күші мынаған тең:

М _А . М- _Л

/=/г

мұндағы М _А -Айдың массасы, ліп, Айға берілетін үдеу:

Бұл үдеу жерге қарай бағытталады. Бұл тендікке (2) формула бойынша £о-дін мәнін енгізсек, онда

Бұл- үдеу дөңгелек орбита бойымен Жерді айнала қозғалғандағы Айдын, центр-ге тартқыш үдеуі болады. Астрономиялық бақылаулар бойынша, Жерден Айға дейінгі қашықтық Жердің радиусынан 60 есе артык, сонда

Екінші жағынан, Айдың осы центрге тартқыш үдеуін кинематика тәсілі-мен есептеп табуға да болады:

~ . 7"2 '

мұндағы V - Айдьщ орбита бойымен қозғалғандағы сызықтық жылдамды-ғы, Т - Айдын, Жерді айналу периоды, бұл 27 тәулік 7 сағат 43 минутқа тең немесе 2 360 580 сек; ал К = 60- Л _ж =60 -6370 км; осы мәліметтерді пайда-ланғанда

4тс2-60- 6370-Ю ⁵ см ^щ л = ~(2"36О 580) 2 сек^ ⁼⁰ - ²⁷ ^см ' ^сек ■

болып шығады.

Сөйтіп, Айдың цеитрге тартқыш үдеуін екі түрлі тәсілмен есептегенде-шықкан нәтижелер бірдей болып отыр; бұл (1) формуланын, дұрыс екендігін көрсетеді.

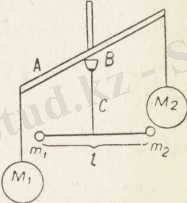
Тартылыс тұрақтысьшың мәнін ең алғаш 1798 жылы Қэвен-диш иірілмелі таразының жәрдемімен тапқан. Кэвендиш пай-даланған прибордың схемасын 69-суретте көрсетілген. Горизонталь күйентеге (А) әр-қайсысының массасы 158 кг М\ және М ₂ қорғасын шарлар ілінген. Құйентенің астьь нан жылжымайтын В бүркеншігіне жіңішке С сымының бір ұшы байланған, оның екінші ұшына жеңіл / стержені асылған, ол стер-женьнің ұштарына кішілеу Ш\ және т ₂ қор-ғасын шарлар орнатылған; Кэвендиш тәжі-рибесінде бүл шарлардың әрқайсысының массасы 730 г болған. А күйентесін бүрған-да үлкен шарлар кішкене шарларға жақын-дап, оларды ездеріне тартады; ол тартылыс- ⁶⁹ ' ^с УР? ^т -Л ^эвен Д ^иш тәжі-ты ті мен ш ₂ шарлары орнатылған / стерже- Р ^{иОесшін} ^{схемасы} -ні бұрылуынан байқауға болады. С сымы-ның серпімділік қасиеттерін біле отырып, тартылыс күшін өлшеу-ге болады, одан соң һ тартылыс түрақтысының мәнін табады. Кейін Кэвендиш тәжірибесі бірнеше рет қайталанған. /г-ның осЫ: кездегі қабылданған мәні мьшадай:

к = 6, 685- 10- ⁸ см*/г сек ² ;

олай болса (1) формула бойынша: әрқайсысының массасы 1 г екі шардың центрлерінің ара қашықтығы 1 см болса, олар бірін-бірі 6, 685- 10~ ⁸ аина күшпен тартады.

к түрақтысы жай ғана сан емес, оның өлшемділігі бар; оның өлшемділігін мына теңдік бойынша табамыз:

к = -^- гпі •т<і

бұдан

бұған қарағанда СОЗ системасында к тұрақтысы см ³ /г се/с ² -пен өлшөнеді.

Мұнда біз Ньютонның екінші заңынын, ^=пт формуласы бойынша күш бірлігін және оның өлшемділігін тағайындадық, одан соң к тұрақтысының жоғарыда келтірілген өлшемділігін таптык. Алайда бұған керісінше істеуге болады: бүкіл әлемдік тартылыс заңынық (1) формуласындағы тұрақты к = \ және ол өлшемділігі жоқ шама деп үйғарамыз, оның есесіне Ньютонның екін-ші занына жаңа түрақты (к') енгізіп, оны мына түрде жазамыз:

І=к'тха. (3)

Сонда С05 системасын пайдалансак, күш бірлігі етіп әрқайсысының мас-сасы 1 г екі шар, олардың біреуінің центрінен екіншісінің центріне дейінгі ара қашықтық 1 см болғанда, бірін-бірі тартатын күшті аламыз. Күштің бұл бірлі-гі 6, 685 • 10- ⁸ динаға тен, болады.

Бүл жолы күштің өлшемділігі былай өрнектеледі:

ал электр және магнит туралы ілімде бірінен-бірінің айырмашылығы баГекі'СС5^ систем^сы, «электростатикалық, және «электромагниттік» систе-малар қолданылады, мүны II томнан көреміз.

Тартылыс тұрақтысы й-ны біле отырып, Жердің массасы мен тығыздығын және басқа аспан денелерінін, массасын анықтауға болады. (2) формуланы пайдаланып, мынаны табамыз:

енді ауырлық күшінің £о үдеуінің, Жердін, К _ж радиусының және к тарты-лыс тұрақтысының сан мәндерін біле отырып, Жер шарыньщ массасын тіке--лей таба аламыз, сонда оның мәні мынадай екен: М _ж =5, 98 • 10 ²⁷ г. Жер шарының орташа тығыздығын мына формуламен табамыз:

л я

сонда есептей келгенде гі = 5, 5 г/см? болып шығады.

Серігі айнала қозғалып жүрген орталық аспан шырағыньщ массасын бы- лай есептеп табуға болады. Мысалы, М _ш - орталық шырақтын. массасы, М~ оның серігінің массасы, Яі -олардың ара қашыктығы болсын. / тартылыс күші серікке центрге тартқыш үдеу береді, сонда

ал күштің кәдімгі өлшемділігі: [/] = ЛШ~ ² болатын еді. Ньютонның екінші заңындағы к' тұрақтысының (оны «динамикалық түрақты» деп атаса да бо-лады) өлшемділігі болса, ол мынадай болмақ:

1 _ і -з МП

оның сан мәні мынаған тең болады:

= 1, 496- 10 ⁷ гсек ² /см\

Сонымен, әр түрлі заңға сүйеніп, бірліктердің түрліше ССЗ системасын тағайындай аламыз. Бір физикалық шаманың өзінің елшемділігі әр түрлі системаларда түрліше болады. Қәдімгі СС5 системасын «динамикалық» си-стема деп, ал күш бірлігі мен оның влшемділігі тартылыс заңына негізделіп тағайындалған СОЗ системасын «гравитациялық» система деп атауға болады. Бұл системалардың екеуінде де жылдамдықтық, үдеудің және басқа кинема-тикалық шамалардың өлшемділіктері бірдей, бірақ күштің, энергияның, жұ-мыстыц, қуаттың, күштер моментініц т. т. өлшемділіктері әр түрлі болады. Механикада системалардың тек біреуін, «динамикалық» системаны ғана қол-

осыдан келш

мүндағы 7, --серіктін айналыс периоды. Бүдан мынаны табамыз:

_4л 2 Щ

яғни серік орбитасының радиусын және оның айналыс периодын біле оты-рып, орталық аспан шырағының массасын анықтауға болады. Мысалы, Жер орбитасының радиусы мен жылдың үзақтығын біле отырып, Күннің массасын таба аламыз: М _к = 1, 98-10 ³³ г.

(4) формуладан мынаны табамыз: 6ул тендіктін он жағында түрған шама берілген орталық шырақты аинала козғалған оның барлық серіктері үшін түрақты шама болып табылады Осыған каоағанда серіктердің (планеталірдыңі орталык шырақты (Күнді) аиналу іаЕіттаоьшьщ квадраттарыньщ қатынасы олардың орталық шырактан (Күн-Іен) қашыктьіктарыньщ кубының қатынасына тең болады. Бүл заңды плане-?Ілар туралы Кейлер тағайындаған, сондықтан бүл Кеплердщ үшнші заңы деп аталады.

ТАРТЫЛЫС КҮШТЕРІ

§ 33. Инерциялық және тартылыстық масса. Ауырлық күші-нің жұмысы. Физикалық шама масса біріне-бірі тәуелді емес екі негізгі заңға - Ньютонның екінші заңына: / = тш және бүкіл

әлемдік тартылыс заңына: ] = к ~~_г2~~ енеді.

Ньютонның екінші заңында маоса денелердің инерциялық қа-сиеттерін сипаттайды. Ал бүкіл әлемдік тартылыс заңында мас-са денелердің тартылыс өрістерін қоздыру және тартылыс өріс-терінің әсерін сезіну қабілеттіліктерін оипаттайды.

Мынадай сұрау қойылуы мүмкін: жоғарыда айтылған екі заңның екеуіне де енген масса бір физикалық шама ма, немесе олар тек арасында белгілі байланысы бар екі түрлі шама ма? Мәселенің тарихына көз салсақ, Ньютонның екінші заңына қа-тысатын инерциялық масса мен бүкіл әлөмдік тартылыс заңына қатысатын тартылыстық масса туралы үғымдар осылайша келіп шыққан. Бүл маосалардың екеуі, егер оларды жекелеп қарасты-рудан мағына шығатын болса, біріне-бірі пропорционал екенді-гін тәжірибе көрсетіп отыр.

Ең алдымен бүл айтылған ^ ₀ 'еркін түсу үдеуінің барлық дене үшін бірдей болуынан байқалып отыр. Денелер ақиқат еркін түс-кен кездегі £ ₀ үдеуін дәл өлшеу өте қиын, бірақ маятниктің тер-белісін бақылай отырып, ^ ₀ үдеуін едәуір-ақ дәл өлшеуге бола-ды. Инерциялық және тартылыстық массалардың арасындағы пропорционалдықтың орындалатындығын және мұндағы дәлдік

~~₁₀₀₀~~ -ге тең екендігін Ньютонның өзі көрсеткен болатын. Бес^

сель сан алуан заттардан істелген маятниктерді пайдаланып көп-теген тәжірибелер жасаған, ол да осындай қорытындыға келген,

мүндағы пропорционалдық дәлдігі ₆ ге тең болған. Ақы-

рында радиоактивтік заттар үшін де бүл пропорционалдық орын-далатындығы көріоетілді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.