Термодинамиканың бірінші және екінші заңдары: изопроцестерге қолданылуы, жылу сыйымдылықтары, адиабаталық үдерістер және биологиялық жүйелердегі энтропия


Термодинамиканың бірінші заңын изопроцестерде қолдану
Термодинамиканың бірінші заңы.
Термодинамиканың заңы былай дейді:
Дене бір күйден екінші күйге өткенде оның ішкі энергиясының өзгеруі денеге жасалған жұмыс пен дененің қабылдаған жылу мөлшерінің қосындысына тең екенін білеміз.
 (1)
(1)
Егер сыртқы күштердің денеге жасаған жұмысын дененің сыртқы күштерге қарсы жасаған жұмысымен ауыстырсақ, онда осыны ескерсек формула былай жазылады:
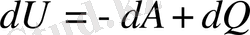 осында
осында
 (2)
(2)
Термодинамиканың бірінші заңы бойынша формуланы былай тұжырымдауға болады. Денеге берілген жылу мөлшері сол дененің ішкі энергиясын өзгертуге және сыртқы күштерге қарсы жұмыс істеуге жұмсалады. Термодинамиканың бірінші заңын энергияның сақталу және айналу заңының жылу құбылысына байланысты айтылған түрі деп те қарастыруға болады.
Термодинамиканың бірінші заңын изопроцестерде қолдану
Газ күйін сипаттайтын параметрлердің екені белгілі. Осы параметрлердің біреуі тұрақты болғанда жүретін процесті изопроцестер деп атайды. Олар Бойль-Мариотт, Гей-Люссак және Шарль заңдарымен анықталатынын көрген едік. Енді термодинамиканы бірінші бастамасын осы процестерге қолданып көрейік.
- Изотериялық процесс. Бұл процесте болады, қысым мен
Температура тұрақты болғандықтан бұл процесс негізінде ішкі энергия өзгермейді, яғни олай болса, термодинамиканың бірінші бастамасы изометриялық процесс үшін былай жазылады:

Біз
 екенін білеміз. Осыдан
екенін білеміз. Осыдан
 тауып алып оны мына формулаға қойсақ:
тауып алып оны мына формулаға қойсақ:
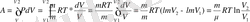
2. Изоқоралық процесс. Бұл процесс
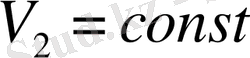 қысым мен температура
қысым мен температура
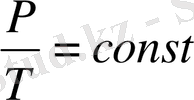 түрінде байланысқан. Изоқоралық процесс үшін
түрінде байланысқан. Изоқоралық процесс үшін
 Олай болса бұл процесс үшін термодинакиканың бірінші бастамасы былай жазылады:
Олай болса бұл процесс үшін термодинакиканың бірінші бастамасы былай жазылады:

3. Изобаралық процесс.
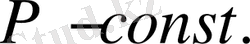 Бұл процесте
Бұл процесте
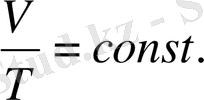 Бұз кезде жұмыс қысымның көлем өзгеруінің көбейтіндісімен анықталады.
Бұз кезде жұмыс қысымның көлем өзгеруінің көбейтіндісімен анықталады.
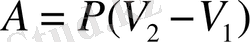 (6)
(6)
Денелердің жылулық қасиеттерін сипатау үшін термодинамикаға жылу сыйымдылық деген ұғым енгізіледі. Денеге берілген және дененің берген жылуы мына формуламен анықталатыны белгілі:
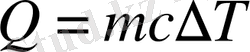 (7)
(7)
Мұндағы
 - дененің массасы, с-дененің меншікті жылу сыйымдылығы,
- дененің массасы, с-дененің меншікті жылу сыйымдылығы,
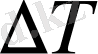 -дене температураның өзгеруі. Біртекті дененің температурасын 1 К-ге көтеру үшін кеткен жылуға тең шаманы заттың меншікті жылу сыйымлыдығы деп атайды.
-дене температураның өзгеруі. Біртекті дененің температурасын 1 К-ге көтеру үшін кеткен жылуға тең шаманы заттың меншікті жылу сыйымлыдығы деп атайды.
Кейбір жағдайларда дененің қызуы немесе сууы кезінде меншікті жылу сыйымдылығы өзгеріп отыруы мүмкін. Олай болса, температураның өзгеруі интервалында температураның өте аз өзгеруін
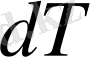 алып, ондағы с-ті тұрақты деп қарастыруға болады, Олай болса:
алып, ондағы с-ті тұрақты деп қарастыруға болады, Олай болса:
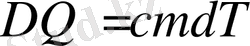 (8)
(8)
Осындан:
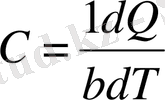 (9)
(9)
Меншікті жылу сыйымдылығымен қатар мольдық жылу сыйымдылығы ұғым да пайдаланылады:
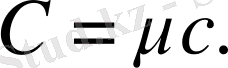 Газдарда жылу сыйымлықтың екі түрі қарастырылады: 1. Көлем тұрақты болғандағы жылу сыйымдылық
Газдарда жылу сыйымлықтың екі түрі қарастырылады: 1. Көлем тұрақты болғандағы жылу сыйымдылық

2. Қысым тұрақты болғандағы жылу сыйымдылық
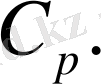 Көлем тұрақты болғанда
Көлем тұрақты болғанда
 жұмыс насы тең болады. Бұл кезде термодинамиканың бірінші заңы (5) формуламен анықталады. Бұл кезде термодинамиканың бірінші заңы денеге берілген жылу түгелімен оның ішкі энергиясын өзгеруге кетеді, олай болса (8) формула бұл кезде мынаған тең болады:
жұмыс насы тең болады. Бұл кезде термодинамиканың бірінші заңы (5) формуламен анықталады. Бұл кезде термодинамиканың бірінші заңы денеге берілген жылу түгелімен оның ішкі энергиясын өзгеруге кетеді, олай болса (8) формула бұл кезде мынаған тең болады:
 (5) формуланы еске алсақ:
(5) формуланы еске алсақ:
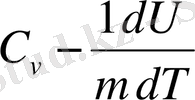 (11)
(11)
Формуладан газдың ішкі энергиясының
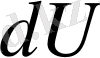 өзгеруі оның температурасының
өзгеруі оның температурасының
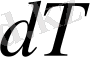 өзгеруіне тура пропорционал екен.
өзгеруіне тура пропорционал екен.
Изобаралық процесте жұмыс
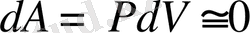 болады. Бұз кезде бір моль газ үшін термодинамиканың бірінші бастамасы былай жазылады:
болады. Бұз кезде бір моль газ үшін термодинамиканың бірінші бастамасы былай жазылады:
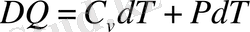 (12)
(12)
осы (12) формуладан газға берілген жылу оның ішкі энергиясын өсірумен бірге жұмыс істеуге де жұмсалатын байқап отырмыз.
Тұрақты қысымдағы мольдың жылу сыйымдылығы
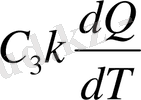 болады, осыдан
болады, осыдан
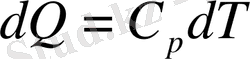 табамыз. Соңғы формуламен (12) формуланы салыстырсақ:
табамыз. Соңғы формуламен (12) формуланы салыстырсақ:
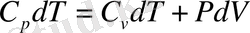 (13)
(13)
Енді менделеев-Клапейрон теңдеуін қолдансақ:
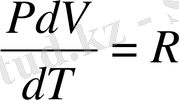 немесе
немесе
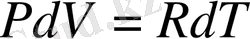 осыны (13)
осыны (13)
Формулаға қойсақ
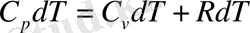
Осыдан
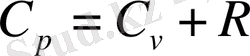 (14)
(14)
Бұл-Майер теңдеуі д. а. Майер теңдеуі тұрақты қысымдағы мольдың жылу сыйымдылығы тұрақты көлемдегі мольдың жылу сыйымдылығына тұрақты қарағанда
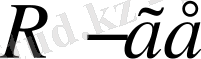 артық екенін көрсетеді.
артық екенін көрсетеді.
Егер газ сыртқа жылу бермесе және сырттан жылу алмаса, ондай процесті адиабаттық процесс д. а. Бұл кезде:

Термодинамиканың бірінші бастамасы адиабат процесс үшін былайша жазылады:
 немесе
немесе
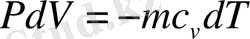
Басқаша айтқанда, ішкі энергияның келуі арқасында жұмыс жасалынады екен. Бір моль газ алайық, яғни
 Сонда (15) формула былай өрнектеледі:
Сонда (15) формула былай өрнектеледі:
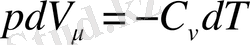 (16)
(16)
Бұл жерде
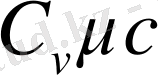 (16) формуланы бір моль үшін өрнектелген Менделеев-Клапейронның теңдеуіне
(16) формуланы бір моль үшін өрнектелген Менделеев-Клапейронның теңдеуіне
 бөлейік. Сонда
бөлейік. Сонда
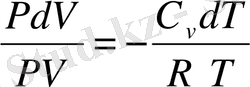 немесе
немесе
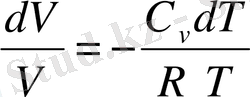
Осыдан
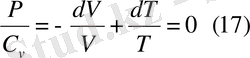
Майер теңдеуінен
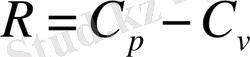 екенін білеміз. Осыны (17) формулаға қойсақ:
екенін білеміз. Осыны (17) формулаға қойсақ:
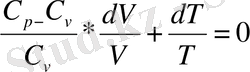
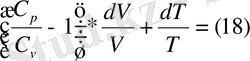
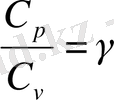
деп белгілесек, онда
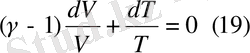
Формуланы интегралдасақ,
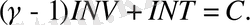 Мұндағы С-тұрақты сан. Соңғы түрлердірсен
Мұндағы С-тұрақты сан. Соңғы түрлердірсен
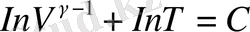 немесе
немесе
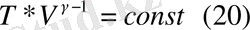 және
және
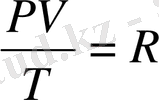 формуланы өрнегіне көбейтсек, шығатыны:
формуланы өрнегіне көбейтсек, шығатыны:
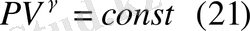 өрнек Пуассон теңдеуі деп аталады. Адиабата процесі кезінде жұмысты табу үшін * формуласын пайдаланамыз.
өрнек Пуассон теңдеуі деп аталады. Адиабата процесі кезінде жұмысты табу үшін * формуласын пайдаланамыз.
Осыдан
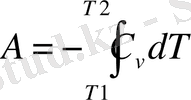
Егер
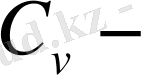 тұрақты десек, онда:
тұрақты десек, онда:
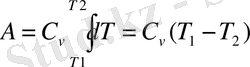
Пуассон теңдеуін пайдалансақ:
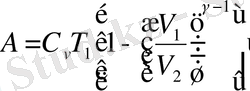
немесе
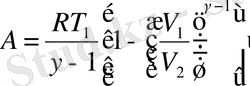
Термодинамиканың екінші заңы
Термодинамиканың 2 заңы өмірде болатын процестердің бағыты жөнінде мағлұмат береді. Бұл заннңы негізін салған француз инженер және физигі Сади Карно. Екінші заңды сипаттайтын бірнеше анықтама бар, олар біріне-бір эквивалентті.
Клаузиус анықтамасы. Жылу ешқашан да суық денеден ыстық денеге берілмейді.
Томсон-Планк анықтамасы. Қыздырғышты суыту арқасында онан алынған жылу мөлшерін түгелімен жұмысқа айналдыру мүмкін емес.
Оствальд анқтамасы. Мәңгі двигательдің екінші түрін жасау мүмкін емес.
Кейде термодинамиканың бұл екі заңын мәңгі двигательдер жасауға болмайтынын дәлелдейтін заңдар деп те атайды.
Бірінші заң. Мәңгі двигательдің бірінші түрін жасау, яғни сырттан энергия алмай жұмыс атқаратын машина жасау мүмкін емес.
Екінші заң. Мәңгі двигательдің екінші түрін жасау, яғни тек бір дененің сууы нәтижесінде жұмыс жасайтын машина жасау мүмкін емес.
Жылу машинасы.
Жылу машинасы деп отынның ішкі энергиясын механикалық энергияға айналдыратын, яғни отын молекуласының ретсіз қозғалысын тәртіпті қозғалысқа түсіретін құралды айтады. Жылу машинасы мынадай бөліктерден тұрады.
- Жұмысшы дене
- Қыздырғыш
- Мұздатқыш
Жұмысшы дене қыздырғыштан
 жылу ясын тоңазытқышқа береді. Мұнда жылу машинасының пайдалы әсер коэффициенті былай есептеледі:
жылу ясын тоңазытқышқа береді. Мұнда жылу машинасының пайдалы әсер коэффициенті былай есептеледі:
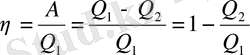
немесе, температура арқылы өрнектесек:
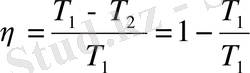
Сонымен, жылу машинасының п. ә. к. бірге тең бола алмайды, яғни машина мұздатқышсыз жұмыс істей алмайды. Бұл да термодинамиканың екінші заңының айтылуының бір түрі.
Энтропия
Жүйедегі ретсіз өлшемін энтропия деп атайды. Егер жүйеде толық тәртіп орнаса, онда энтропия минимум болады. Ретсіздік артқан сайын энтьропия да түседі. Жүйеде толық хаос орнаса, онда энтропия ең жоғарғы мәнге ие болады. Қатты дене, сұйық және газ алайық.
Біз жоғарыда
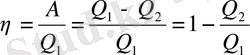 тапқан едік.
тапқан едік.
Осыдан
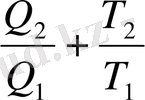 немесе
немесе
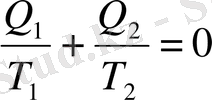 табамыз.
табамыз.
Сондықтан да ол теріс. Олай болса
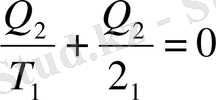 дп жазуға болады.
дп жазуға болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz