Қайталанбалы тәуелсіз сынақтар: Бернулли формуласы, Пуассон және Муавр-Лаплас жуықтаулары


ҚАЙТАЛАНБАЛЫ ТӘУЕЛСІЗ СЫНАҚТАР.
- Қайталанбалы тәуелсіз сынақтар
Егер тәжірибе бірнеше рет жүргізілгенде А оқиғасының әр тәжірибедегі ықтималдығы басқа тәжірибелердің нәтижесіне тәуелсіз болса, ондай тәжірибелерді А оқиғасына қарағанда тәуелсіз тәжірибелер деп атайды.
Әртүрлі тәуелсіз тәжірибелерде А оқиғасының ықтималдығы да әртүрлі болуы, немесе бірдей болуы мүмкін. А оқиғасының барлық тәжірибелердегі
ықтималдығы бірдей болатын жағдайды қарастырамыз.
Егер А оқиғасының әр тәжірибедегі пайда болу ықтималдығы р болса, онда
А оқиғасының пайда болмау ықтималдығы әр тәжірибеде q = 1-p болады.
А оқиғасының п тәуелсіз тәжірибеде к рет пайда болуының, ендеше п-к рет
болмауның ықтималдығын табу керек. Іздеп отырған ықтималдықты
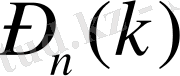 арқылы белгілейміз. Мысалы, Р
6
(4) символы 6 тәжірибеде А оқиғасы 4 рет пайда болады, ендеше 2 рет пайда болмайды деген ұғымды береді. Бұл есепті Бернулли формуласы шешеді.
арқылы белгілейміз. Мысалы, Р
6
(4) символы 6 тәжірибеде А оқиғасы 4 рет пайда болады, ендеше 2 рет пайда болмайды деген ұғымды береді. Бұл есепті Бернулли формуласы шешеді.
Муавр - Лапластың локальдық теоремасы.
Оқиғаның әрбір тәжірибеде пайда болу ықтималдығы р - тұрақты (0<p<I) болса, онда оқиғаның n тәулсіз тәжірибеде k рет пайда болуы у функциясының жуық мәніне тең болады. n неғұрлым үлкен болған сайын функция мәні соғұрлым дәл.
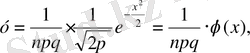
мұндағы
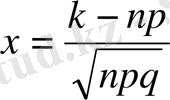
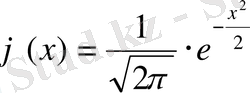
Функцияның мәндерінің, x>0 үшін, кестесі берілген. Ал x<0 болғанда да осы кестені қолдануға болады, себебі
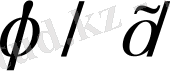 функциясы жұп функция,
функциясы жұп функция,
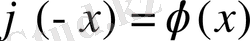 .
.
Сонымен А оқиғасы n тәжірибеде k рет пайда болу ықтималдығының жуық мәні мынаған тең:
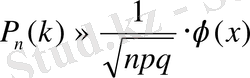 ,
,
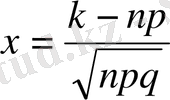
Жауаптарын салыстырсақ, бірталай айымашылық бар екенін көреміз, себебі, n кіші сан, ал Лапластың жуықтап есептеу формуласы n жеткілікті үлкен мән алғанда ғана жақсы дәлдікпен есптейді.
Қарастырылған екі формулада оқиғаның бір тәжірибедегі пайда болу ықтималдығы р жеткілікті түрде үлкен сан, яғни егер р 0 мен 1 аралығында өзгереді десек, бұл екі жағдайда 0, 1<p<1 болады.
Егер
 , ал
, ал
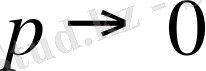 , яғни
, яғни
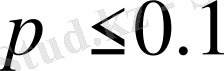 болса, және k - ның мәні де жеткілікті түрде аз сан болса, онда ізделінді ықтималдықты есептеуге Пуасонның жуықтап есептеу формуласы қолданылады.
болса, және k - ның мәні де жеткілікті түрде аз сан болса, онда ізделінді ықтималдықты есептеуге Пуасонның жуықтап есептеу формуласы қолданылады.
Лапластың интегралдық теоремасы
n рет тәуелсіз тәжірибе жасалынды делік. Әр тәжірибедегі А оқиғасының пайда болу ықтималдығы р - ға тең (0<p<1) .
n тәжірибеде А оқиғасының
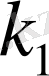 - ден кем болмау,
- ден кем болмау,
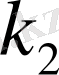 - ден көп болмау ықтималдығын
- ден көп болмау ықтималдығын
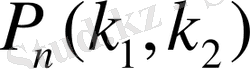 қалай табуға болады? Бұл сұраққа Лапластың интегралдық теоремасы жауап береді.
қалай табуға болады? Бұл сұраққа Лапластың интегралдық теоремасы жауап береді.
Теорема.
А оқиғасының әр тәжірибеде пайда болу ықтималдығы р тұрақты, 0 мен 1 - ге тең болмаса, онда n тәжірибеде А оқиғасының пайда болу саны
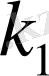 - ден кем болмау,
- ден кем болмау,
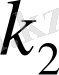 - ден аспау ықтималдығы
- ден аспау ықтималдығы
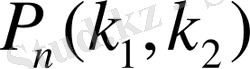 жуық шамамен анықталған интегралға тең:
жуық шамамен анықталған интегралға тең:
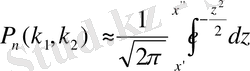
мұндағы
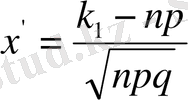 және
және
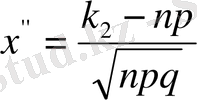
Анықталмаған интеграл
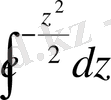 элемент р функциялар арқылы өрнектелмейтін болғандықтан, есепті шешуде арнайы кестелер қолданылады. Егер
элемент р функциялар арқылы өрнектелмейтін болғандықтан, есепті шешуде арнайы кестелер қолданылады. Егер
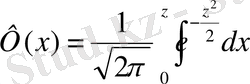 болса, онда функция
болса, онда функция
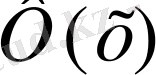 Лаплас функциясы деп аталады. Арнайы кестелер
Лаплас функциясы деп аталады. Арнайы кестелер
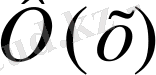 функциясының х - тің оң мәндеріндегі, дәлірек айтқанда
функциясының х - тің оң мәндеріндегі, дәлірек айтқанда
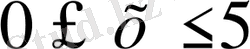 алатын мәндері келтірілген, х<0 болғанда да осы кесте қолданылады, тек бұл жағдайда
алатын мәндері келтірілген, х<0 болғанда да осы кесте қолданылады, тек бұл жағдайда
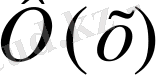 функциясының тақ екенін ескеру керек, яғни
функциясының тақ екенін ескеру керек, яғни
 = -
= -
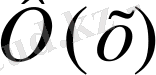 , ал x>5 болғанда
, ал x>5 болғанда
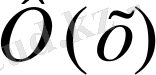 =0, 5 деп алынады.
=0, 5 деп алынады.
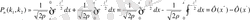
Сонымен А оқиғасының n тәжірибеде
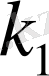 -ден
-ден
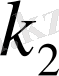 -ге дейін пайда болу ықтималдығы мынаған тең:
-ге дейін пайда болу ықтималдығы мынаған тең:
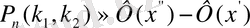
мұндағы
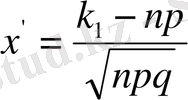 және
және
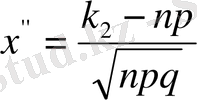
2. Бернулли формуласы.
А оқиғасының n тәуелсіз тәжірибенің әрбіреуіндегі пайда болу ықтималдығы бірдей және p-ға тең болса (
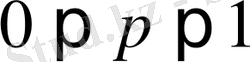 ), осы оқиғаның n тәжірибеде к-рет пайда болу ықтималдығы
), осы оқиғаның n тәжірибеде к-рет пайда болу ықтималдығы
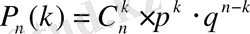
формуласы арқылы өрнектеледі.
Бұл формуланы Бернулли формуласы деп атайды.
Мұндағы
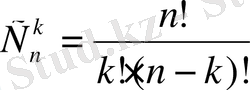 ;
;
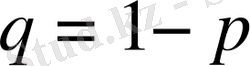
А оқиғасының n тәуелсіз тәжірибеде:
а) к реттен аз; б) к реттен көп; в) к реттен кем емес; г) к реттен көп емес пайда болу ықтималдықтары сәйкес төмендегі формулалармен есептеледі:
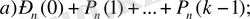
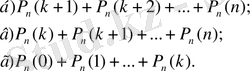
Мысал.
4 баласы бар отбасында 3 ұл және 1 қыз бала болу ықтималдығын анықтау керек. Ұл және қыз баланың туу ықтималдығы бірдей.
Шешуі. . Ұл баланың туу ықтималдығы р=0, 5, онда қыз баланың туу ықтималдығы да q = 1-p=0, 5 және п=4, к=3.
Ізделінді ықтималдық
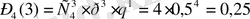 ; себебі p=q=0, 5.
; себебі p=q=0, 5.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz