Дифференциалдық есептеулер элементтері: теориясы және қолданылуы


... жалғасыСәтбаев қаласы
№ 1 мектеп-гимназиясы
Ибраева Гүлжазира Зейнуллақызы
8 cынып
«Математикадағы дифференциалдық есептеулер элементтері»
Секция: алгебра
Жетекшісі: Бектепбергенова З. Д.
2010 жыл
Мақсаты: Жоғарғы математикада қарастырылатын белгілі дифференциалдық есептеулер элементтері бойынша мектеп матиматикасындағы туындыларды табу үшін қолдануға болатынын көрсету.
Кіріспе
Туындылар және оларды функцияларды зерттеуде қолданылуы қарастырылатын математиканың бөлімі дифференциялдық есептеу деп аталады. Айырманы көрсететін Δƒ түріндегі өсімше туындыларымен жұмыс істегенде елеулі орын алады. Сондықтан да жаңа есептеу calculis differentialis ( қазақша айырмаларды есептеу деп аударылады) атауында латынша differentia (айырма) түріде көрініс табуы орынды, бұл атау XVII ғасырдың аяғында, яғни жаңа әдіс дүниеге келгенде пайда болды. «Туынды» термині derivee деген француз сөзінің қазақша сөзбе-сөз аудармасы, және оны 1797 жылы француз математигі Ж. Лагранж (1736-1813) енгізген, қазіргі кездегі ý', ƒ' белгілеулерін де сол енгізген. Бұл атау мынадай ұғымның мағынасын ашады:ƒ'( x ) функциясы ƒ( x ) -тен шығады, ƒ( x ) -тің туындысы болып табылады. Ағылшын математигі И. Ньютон ( 1643-1727) функцияның туындысын флюксия деп атайды, ал функцияның өзін флюксия деп атаған. Неміс математигі Г. Лейбниц (1646-1716) дифференциялдық қатынас туралы айтқан және туындыны
түрінде белгілеген. Бұл белгілеу қазіргі әдебиетте де жиi кездеседі. Неміс математигі Г. Лейбниц (1646-1716) df символын f функциясының дифференциалын белгілеу үшін таңдап алған. f функциясының дифференциалын - ƒ'(х
) туындысыны Δ х өсімшесіне көбейтіндісі, яғни df= ƒ'(х
) . Δ х ; Δ х белгілеуін dx -пен алмастырып, оны былай да жазуға болады:
df= ƒ'(х
) dx
осыдан
ƒ'(х
) =
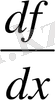
Дифференциялдың геометриялық мағынасын 1-суреттен анық көрінеді: мұнда df=AB, 1түзуі-графикке жүргізілген жанама.
3
Дифференциялдық есептеуде қабылданған терминология туралы әңгімені шек және шексіз аз ұғымдары толықтыра түседі. Шек туралы төменде айтылады. Әзірге мынаны ескертеміз, мысалы, туынды барлық нұсқауларда шек ретінде анықталады. Жоғарыда қабылданған Δх→() жағдайда
→ ƒ'(х
)
деп жазудың орнына ƒ'(х
) =
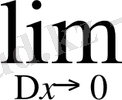
түрінде жазады. Lim белгілеуі - латыннның limes(меже, шекара) деген сөзінңі қысөарған түрі: мысалы, Δх -ті кеміте келіп, біз
мәнін ƒ'(х
) «шекарасына» ұмтыламыз. «Шек» терминін ағылшын математигі И. Ньютон(1643-1727) енгізген. Δх-тен (Δх)
квадрат функциясы шексіз аз шаманың мысалы бола олады, өйткені Δх→() жағдайда (Δх)
→() . Жалпы егер limά(x) =0 болмаса, ά(x) -шексіз аз деп атайды. Математикалық анализде шексіз аздар маңызды орынға ие, сондықтан да оны көбінесе шексіз аздар анализі деп атайды. Қазақша maximum-ең үлкен, ал minimum-ең кіші деп аударылады. Дифференциялдық есептеуді ағылшын математигі И. Ньютон(1643-1727) мен неміс математигі Г. Лейбниц (1646-1716) біршама беріректе, ғасырдың соңыңда құрды. Таңқаларлық бір нәрсе, бұдан көп жыл бұрын грек математигі Архимед ( б. з. д. 287-212) аса күрделі спираль сияқты қисыққа жанама жүргізу есебін шығарған ( ол мұнда шекке көшуді қолданған), сонымен бірге ƒ( x ) = х
(a-x) функциясының максимумын таба білген. Жанама ұғымы итальян математигі Н. Тартальи(1499-1557) еңбектерінде ауық-ауық ұшырасын қалады, мұнда жанама зеңбіректің оқты барынша алысқа атуға көмектесетін көлбеулік бұрышы жөніндегі мәселені оқып - үйрену барысында айтылады. австрия алымы И. Кеплер(1571-1630) радиусы берілген шарға іштей сызылған параллелипипедтің ең үлкен көлемі туралы есепті шығару барысында жанаманы қарастырған. XVII ғасырда итальян ғалымы Г. Галилейдің(1564-1642) қозғалыс туралы ілімі негізінде туындының кинематикалық концепсиясы қарштап өркендеді. Әр түрлі есептерді шығаруға қолданылған алуан түрлі варианттардың баяндалуы француз математигі Р. Декарт(1596-1650), француз атематигіРобервальде (1602-1675), ағылшын ғалымы И. Барроу (1630-1677) мен И. Ньютон еңбектерінде кездеседі. Жанама мен нормалды(жанама перпендикуляр және жанасу нүктесінде жүргізілген түзу осылай аталады) қарастыруға француз математигі Р. Декарт (1596-1650) линзалардың оптикалық қасиеттерін зерттеу барысында келді. Ол аналитикалық геометрия әдістерінің және өзі ойлап тапқан анықталмаған коэфициенттер әдісінің
4
көмегімен бірқатар қисықтарға, соның ішінде элипске нормалдар салу туралы есепті шығара білді. 1629 жылы француз математигі П. Ферма(1601-1665) көпмүшелердің экстремумдарын табу ережелерін ұсынды. Айта кететін елеулі нәрсе, Ферма осы ережелерді қорытып шығарғанда, мавксимум мен минимумдардың қарапайым дифференциялдық шартын біле отырып, шекке көшуді қауырт қолданды. Туындылар туралы ғылымды жүйелі түрде дамытқан неміс математигі Г. Лейбниц (1646-1716) пен ағылшын математигі И. Ньютон (1643-1727) жылы болды, олар анализдің негізгі екі проблемасын тұжырымдады. 1. «Жүретін жолдың тұрақты ұзындығы берілген, көрсетілген уақыт ішіндегі қозғалыс жылдамдығын табу керек. 2. Қозғалыс жылдамдығы тұрақты, көрсетілген уақыт ішінде жүрілген жолдың ұзындығын табу керек». Бірінші проблема дифференциялдық есептеудің даму бағдарламасын береді, екіншісі интегралдық есептеуге жатады. Ньютон механика есептерін негізге алса (ньютондық анализ ньютондық классикалық механикамен қатар жасалған-ды), Лейбництің артықшылығы ол геометрия есептеріни негіз етіп алды. Француз математигі А. Лопиталь ( 1661-1704), швейцария математигі И. Бернуллиден (1667-1748) дәріс алған, ол жылдың өзінде дифференциялдық есептеудің алғашқы курсы «Қисық сызықтарды зерттеуге арналған шексіз аздар анализін» баспадан шығарып үлгерді, бұл жаңа әдістердің таралуына септігін тигізді. Математикалық анализдің дамуына швейцария математигі Л. Эйлер(1707-1783) мен неміс математигі К. Ф. Гаусс(1777-1855) теңдесі жоқ үлес қосты. Функцияларды дәрежелік қатарларға жіктеу, яғни функцияларды қосылғыштарының саны шектеусіз көпмүшелер түрінде көрсету жөнінде болып отыр. Шектусіз қосындылардың (сан қатары) мысалы бізге таныс, мәселен шексіз периодты бөлшектерді қосылғыштарының саны шектеусіз қосынды түрінде көрсету. Сандық және функциялық қатарлармен Ньютон ғана емес, одан бұрынғылар да шұғылданған болатын, сондықтан да мынадай тамаша қатыс үшін f( х
+ Δх) = ƒ'(х
) +
. Δх+
. ( Δх ) + . . . +
. ( Δх )
+ . . . (мұндағы:
функциясын х
нүктесінде n- рет дифференциялаудан шыққан мән, ал n!=1 2…n ) Қабылданған Тейлор формуласын атамай кету дұрыс болмас еді. ((Б. Тейлор (1685-1731) -ағылшын математигі, формуласы 1715 жылы жарық көрген) . Туындылар формулаларын біле отырып, мысалы пен функциялары үшін, оларды өзіміз Тейлор қатарына жіктей аламыз. Кейбір жағдайларда, қосылғыштардың шектеусіз санын ескермей тастап кетіп, көпмүшелермен берілген функциялар жап-жақсы жуықтау беретін формула шығарып алуға болады екен. Шығарылатын есептер шеңберін кеңейтуге мүмкіндік беретін қуатты жаңа әдістерін пайда болуынан туған сезім XVIII ғасырда анализдің қарақынды дамуына себепші болды. Алайда осы ғасырдың соңында дифференциялдық және интегралдық есептеулерді жасаушыларда аса өткір проблемалар пайда болды. Негізгі қиыншылық мынада еді:шек, үзіліссіз, нақты сан сияқты негізгі терминдердің дәл анықтамалары болмады(осыған сәйкес пайымдауларда логикалық жағынан олқылықты кейде қателіктер болды) . Бұған тән мысал - үзіліссіздік анықтамасы. Л. Эйлер, Лагранж сияқты математиктер, тіпті, анықталу облысында бір ғана өрнекпен белгілейтін функцияны үзіліссіз деп атайды. Анализдің берік ірге тасын қалауға шешуші қадамды өткен ғасырдың 20 -жылдарында француз ғалымы О. Коши (1789-1857) жасаған еді, ол функциямен тізбектің шектерінің дәл анықтамаларын ұсынды және соларды негіз ете отырып, анализдің көптеген іргелі теоремаларын дәлелдеді. Бұдан біршама бұрын (1821) математик Б. Больцано (1781-1848) шек пен үзіліссіздіктің анықтамаларын, басқа да бір қатар тамаша нәтижелерге (соның ішінде аралықта үзіліссіз, бірақ оның ешбір нүктесінде туындысы болмайтын функцияның мысалы бар) қол жеткізген еді, бірақ оның жұмыстары көптен кейін белгілі болды. Функция шегінің Коши берген анықтамасы былай тұжырымдалады: «егер кез келген έ>0 саны үшін δ>0 саны табылып, 0<│x-a│< δ теңсіздігін, қанағаттандыратын барлық x үшін│ f(x) -A │<ε орындалатын болса, онда А саны f(x) функциясының х а-ға ұмтылғандағы шегі деп аталады(яғни
f(x) =A ) ». Осы анықтамаға сүйеніп, функцияның нүктедегі үзіліссіздігіне анықтама беру қиын емес:егер
f(x) = ƒ(х
) . болса, онда f функциясы нүктесінде үзіліс болады. Тізбек шегінің (интегралдың анықтамасы дәл осы ұғыммен байланысты) анықтамасы былай тұжырымдалады: «Егер кез-келген έ>0 үшін N нөмірі табылып, барлық n>N болғандағы│
-A│< έ теңсіздігі тура болса, онда А саны
тізбегінің шегі болады». Коши шектер туралы мынадай теоремаларды дәлелдеген, оларды біз туындыларды есептеген кезде пайдаланғанбыз:, егер
f(x) =A және
g(x) =B болса, онда қосынды мен айырманың, көбейтіндінің, бөліндінің шектері бар
болады(
g(x≠0) және
( f(x) ± g(x) =A+B
( f(x) g(x) =AB
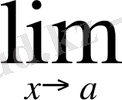
=
«Кошише» (көбінесе «энсилон -дельта тілінде»деп атайды) дәлелдеуге мысал келтірейік. Қосындының шегі туралы теореманы дәлелдейік. Кез келген έ>0 оң санын аламыз . Сонда
Equation. 3 болады да, сондықтан (Коши анықтамасы бойынша) 1)
f(x) =A шартынан δ
>0 саны табылып, │x-a│< δ
теңсіздігін қанағаттандыратын барлық х үшін │ f(x) -A │<
(1) болатындығы шығады. 2)
g(x) =B шартынан δ
>0 саны табылып, │x-a│< δ
теңсіздігін қанағаттандыратын барлық х үшін │ g(x) -B │<
(2) болатындығы шығады. δ
мен δ
сандарының ең кішісін δ арқылы белгілейміз. Сонда 0<│x-a│< δ теңсіздігін қанағаттандыратын кез келген х үшін (1) мен (2) теңсіздіктер орындалады; осындай х-тер үшін былай болады: │ f(x) + g(x) -(A+B) │=│(f(x) -A) + (g(x) -B) │≤│f(x) -A│+ │ g(x) -B ││<
+
=ε Осымен
│( f(x) + g(x) │=A+B болатыны дәлелденді. Басқа ережелер де (көбейтінді мен бөлінді үшін) осылайша дәлелденді. XVII ғасырда математикада болған төңкерістердің тереңдігінің айқын сипаттамаларын Карл Маркс (1818-1883) пен Фридрих Энгельс (1820-1895) берген болатын. Алайда математиканың Франция, шектеусіз аз шамалар, мектер мен туындылар ұғымдарымен байланысты жаңа тармақтарының дамуының бастапқы кезеңіне Маркс «мистикалық» деген сипаттама берген-ді.
7
XVII ғасыр математиктерінің үраны мынадай болған: «Алға қарай қозғала беріңдер, ал нәтижелердің дұрыстығына сенім өзінен-өзі келеді». Шынында да, Кошидің ғылыми еңбектерінен кейін XIX ғасырда анализ бастамаларына логикалық негіздеме берді, басқа математиктер одан әрі дамытты.
Туындының анықтамасы Туынды ұғымы өзара байланысты екені алдын ала екі есепті пайда болды - ол қисыққа жанама жүргізу және қозғалып бара жатқан дененің жылдамдығын табу есептері. Осы екі есеп бір-біріне өзге білім салалары - геометрия мен механикаға да жатса да, олар тек қана бір математикалық амалға
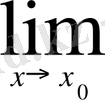
-түріндегі шектітабу есебіне әкелді. Әрине, бұл амалдың арнаулы атауы болуы керек. Ол амалдың өзін функцияны дифференциалдау, ал оның нәтижесін, яғни шектің мәнін функцияның туындысы дейді.
Сөйтіп, функциясы І аралығында анықталсын. Егер
Є I үшін
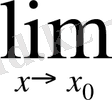
нақты мәнді шегі бар болса, онда f функциясын
нүктесінде дифференциалданады, ал шектің мәнін f функциясының
нүктесіндегі туындысы дейді де, f``(
) символымен белгілейді. Осы анықтамаға сүйене отырып, жоғарыда талқыланған есептерді былай тұжырымдауға болады.
. Егер f функциясының
нүктесінде туындысы бар болса, онда сол нүктеде y=f(x) қисығының жанамасы бар болып, оның теңдеуі: y= f(
) . (х-
) +f(
) болады. (2) түзуін а функциясының графигінің (
, f(
) ) нүктесіндегі жанамасы деп те атайды. (*) теңдеуінен жанаманың бұрыштық коэффиценті сол нүктедегі туындының мәніне тең екенін көреміз. Басқаша айтқанда, жанама мен х-тер осінің арасындағы бұрыш а болса, онда f``(
) = tgά теңдігі орындалады. Бұл туындының геометриялық мағынасы болады.
8
. Материялдық нүктенің қозғалысы жоғарыда айтылғандай f(t) функциясы арқылы бейнеленген болсын. Егер f(
) туындысы бар болса, онда сол туынды материялдық нүктенің
мезгіліндегі жыдамдығы деп аталады. Туындының анықтамасын шекті белгілейтін символдарды қолданып, былай жазуға болады:
.
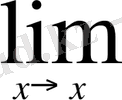
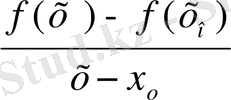
.
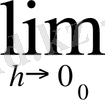
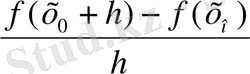
.
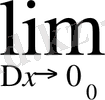
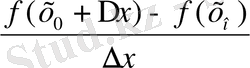
.

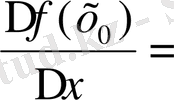
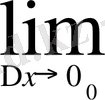
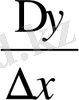
Соңғы екі анықтамада Δx =x-
, Δy=f(x) - f(
) немесе Δx =(
+Δх) -
, Δf(
) =Δy f (
+Δх) - f(
) белгілеулері қолданылған. Δx x-
= h сандары функцияның аргументінің немесе тәуелсіз айнымалының өсімшесі деп аталады. Туындының анықтамасындағы қатынас мағынасының жоғалтпауы үшін, һ өсімшесі (анықтық үшін һ-ты алдық) нөлден өзге болуы қажет. Бірақ бұл жағдайдың анықтамадағы шекке зияны болмайды, өйткені шектің таңбасынан кейін тұрған
φ(h) =
өрнегі сол өсімшенің функциясы ретінде қарастырылып,
φ(h) шегінің өзі өсімше нөлге ұмтылғанда алынады. Әрине, һ өсімшесі оң да, теріс те бола алады, тек қана
+h саны функциясының анықталу жиынынан шығып кетпеуі керек. f(x) - f(
) = f(
+h) - f(
) f (
+Δх) - f(
) =Δy cандарын функцияның өсімшесі дейді. Сөзбен
-
анықтамалары былай айтылады:егер функцияның өсімшесінің өзінің пайда болуына себепші болған тәуелсіз айнымалының өсімшесіне қатынасының соңғы өсімше нөлге ұмтылғанда нақты мәнді шегі бар болса, онда функция дифференциалданады деп, сол шектің мәні функцияның туындысы деп аталады. Біз көбінесе туындының анықтамасының алғашқы екі түрін пайдаланамыз.
9
Туындының мынадай белгілері бар: Г. Лейбниц:
,
немесе
(1675ж. берілген), Ж. Лагранж: f(
) немесе у (1770ж. берілген), О. Коши: Df(
) немесе Dy (1800ж. берілген) .
Негізгі бөлім
2. 1. Функцияның туындысы Жалпы білім беретін оқу бағдарламасы бойынша оқытылатын ең бірінші «Функцияның өсімшесі» тақырыбы беріледі. Мұнда «аргумент өсімшесі» және «функция өсімшесі» деген ұғымдар пайдаланылады. Олардың мағынасы былай түсіндіріледі: х қандай да бір белгіленіп алынған нүктесінің маңайында жатқан еркін алынған нүкте. x-
айырмасын тәуелсіз айнымалының
нүктесідегі өсімшесі (немесе аргументтік өсімшесі) деп атайды да, Δx деп белгілейді. мұндағы: Δx =x-
бұдан: x=
+Δx Аргументтің бастапқы
мәні Δx өсімше алды деп те атайды. Осының салдарынан функциясының мәні f(x) - f(
) = f(
+Δx) - f(
) шамасына өзгереді. Бұл айырма
нүктесіндегі Δx өсімшесіне сәйкес f функциясының өсімшесі деп аталады және Δf символымен белгіленеді, яғни анықтама бойынша Δf= f(
+Δx) - f(
) (1. 1) Бұдан f(x) = f(
+Δx) = f(
) +Δf Мұндағы Δf өсімшесі Δx-тің функциясы
Мысал: 1
Егер f(x) =
,
=2 және x=1. 9 болғанда
нүктесіндегі Δx және Δ f өсімшелерін табайық. Δx= x-
= 1. 9-2=-0. 1, Δ f=f( 1. 9 ) -f(2) =
-
=- 0. 39 Функцияның өсімшесінен кейін, «Туынды туралы ұғым»тақырыбы өтіледі.
10
Мұнда 1. Функция графигіне жүргізілген жанама туралы ұғым 2. Қозғалыстың лездік жылдамдығы туралы есептер беріледі. Содан кейін туындыға анықтама беріледі. Ол мына тұрде беріледі: Δx нөлге ұмтылғанда
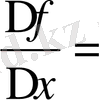
(1. 2) айырмалық қатынас ұмтылатын сан f функциясының
нүктесіндегі туындысы деп аталады. f функциясының
нүктесіндегі туындысы
(
) деп белгіленеді. Мысал. 2. f(x) =
функциясының нүктесіндегі
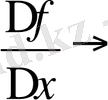
і туындысын табайық. Жоғарыда айтылған схема бойынша жұмыс істейміз. 1) Δ f=(
+Δx)
-
=
Δx+3
(Δx)
+ (Δx)
2)
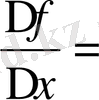
Δx+3
(Δx)
(Δx≠0) 3)
қосылғыштары тұрақты екенін байқаймыз, ал Δx→0 жағдайда 3
Δx→0 және (Δx)
→0, дeмек, 3
Δx+ (Δx)
→0. Сонда Δx→0 жағдайда
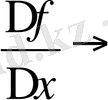
. Сонымен, туынды тақырыбын өткенде бұл сыныптарда «ұмтылады» деген ұғым пайдаланылады, бірақ шек ұғымы бұған дейін қарастырылмаған. Бұл тақырыптардан кейін «Функцияның үзіліссіздігі мен шекке көшу туралы ұғым» тақырыбы беріледі. Мұнда қозғалыстың лездік жылдамдығы турады есеп қарастырылады. ν
(Δt) =ν
- gt
-g
функциясы Δ t=0 болғанда анықталмаған. Бірақ L= ν
- gt
саны үшін│Δt│ азайғанда ν
(Δt) -L айырмасы нөлге жуықтайды. Сол себепті де біз Δt→0 жағдайда ν
(Δt) =ν
- gt
деп жаздық. Жалпы былай айтады:егер│Δx│ кемігенде f(x) -L айырмасы мейлінше аз, яғни │ f(x) -L │кез келген белгілеп көрсетілген h φ 0 санынан кем болып шықса, онда х 11
саны
-ге ұмтылғанда, f функциясы L санына ұмтылады. x-
oрнына, әрине Δx→0 деп жазуға болады. f функциясы L функциясы бойынша L санын табу шекке көшу деп аталады. Төмендегі негізгі екі жағдайда шекке көшумен кездесеміз. 1-жағдай, бұл
айырмалық қатынасында шекке көш, яғни туындыны табу. Бұл жағдаймен біз таныспыз. 2-жағдай, функцияның үзіліссіздігі ұғымымен байланысты. Егер x→x

жағдайда f(x) →f(x
) болса, онда бұл функцияны x
нүктесінде үзіліссіз деп атайды. Мұнда f(x) -L=f(x) -f(x
) =Δx . │ Δx │аз болғандa│ Δf │те аз болатын, яғни x
нүктесіндегі аргументтің аз өзгерулеріне функция мәндерінің де аз өзгерулері сәйкес келетіні шығады. Үзіліссіздік пен шекке көшудің анықтамаларынан 3 ереже беріледі: 1-ереже:Егер f функциясы x
нүктесінде үзіліссіз болса, онда Δx→0 кезде Δ f →0 2-ереже:Егер f функциясы x
нүктесінде туындысы бар болса, онда Δx→0 кезде
→ f''( x
) 3-ереже: x→x
кезде f(x) →A g(x) →B болсын A) f(x) + g(x) →A+B Б) f(x) g(x) →AB В)
→
Үзіліссіз функциялар f және g үшін
A= f(
), B=g(
) Және бұл ережелер
нүктесінде үзіліссіз функциялардың қосындысы, көбейтіндісі және бөліндісі де
нүктесінде үзіліссіз болады(дербес жағдайда g(
) ≠ 0 ) дегенді білдіреді. Шекке көшу ережелері функциялардың үзіліссіздігін дәлелдегенде және дифференциалдау формулаларын қорытып шығарған кезде кең пайдаланылады, бірақ шек ұғымы берілмеген. Туындыларды есептеу ережелері былай беріледі: 1-ереже:Егер u және ν функциялары
нүктесінде дифференциалданатын болса, онда 12
олардың қосындысы да сол нүктеде дифференциалданады және ( u+ν) '=u'+ν' 2-ереже:Егер u және ν функциялары
нүктесінде дифференциалданатын болса, онда олардың көбейтіндісі де сол нүктеде дифференциалданады және ( uν) '=u'ν+uν'̀ (1. 3) Салдар:Егер u(x) функциясы
нүктесінде дифференциалданатын, ал С тұрақты болса, oнда Cu функциясы дда сол нүктеде дифференциалданады және ( Cu) '=Cu ̀ (1. 4) Қысқаша былай делінеді:тұрақты көбейткішті туынды таңбасының алдына шығаруға болады. 3-ереже: Егер u және ν функциялары
нүктесінде дифференциалданатын болса және ν функциясы сол нүктеде нөлге тең болмаса, онда
бөліндісі де сол нүктеде дифференциалданады және
'=
(1. 5) Дәрежелік функцияның туындысы. Дәрежелік x
функциясының, мұндағы n - еркін алынған 1-ден артық натурал сан, туындысын есептеуге арналған формула мынадай: (x
) '= nx
(1. 6) Бұл ережелер дәлелдеулермен беріледі. Осы ережелерді қолдану арқылы функциялардың туындылары табылады.
«Күрделі функцияның туындысы»тақырыбын өткен кезде, алдымен күрделі функция туралы түсінік мысал арқылы беріліп түсіндіріледі. Мысал z=h(x) =
формуласымен берілген. h функциясының х-тің берілген мәні бойынша сәйкес z мәнін есептеп шығару қажет болсын. Ол үшін біз ең алдымен х-тің берілген мәні бойынша y=f(x) =1-x
мәнін, сонан соң у бойынша z=g(y) =
мәнін есептеп шығарамыз. Сөйтіп f функциясы х-ті у-ке ауыстырады, ал g функциясы y-ті z-ке ауыстырады. h-g мен f функцияларынан құралған күрделі функция делінеді және былай жазылады:
h(x) =g(f(x) ) (1. 7)
13
h(x) =g(f(x) ) күрделі функцияның еркін алынған нүктесіндегі мәнін есептеу үшін, ең алдымен сол нүктедегі «ішкі» f функциясының у мәнін, сонан соң g(y) мәнін есептейді. Күрделі функциясының туындысының формуласы. Егер f функциясының
нүктесінде, g функциясының y
= f(x
) нүктесінде туындысы бар болса, онда күрделі h(x) =g(f(x) ) функциясының да
нүктесінде, туындысы бар болады және h(x
) =g(f(x) ) . f(
) (1. 8) Мысал h(x) =
функциясының туындысын табу керек. h(x) =g(f(x) ) , мұндағы y=f(x) =3x
+1, g(y) =
болғандықтан, g(y) =
және y= f(x) =6x бұдан h
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz