Тригонометриялық Фурье қатарларын күшті қосындылау және үзіліссіздік модулі


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 36 бет
Таңдаулыға:
Ф-ОБ-001/003
Қазақстан Республикасы Білім мен ғылым министрлігі
Қожа Ахмет Ясауи атындағы Халықаралық қазақ- түрік Университеті
«Математика» кафедрасы
Дипломдық жұмыс
Тақырыбы: Тригонометриялық Фурье қатарларын күшті қосындылау
Орындаған: ЖМА-511 тобының студенті
Илебаева И.
Ғылыми жетекшісі:
Ф. -м. ғ. к., доцент Тазабеков С.
Түркістан 2009
2
Мазмұны
Кіріспе . . . 3
І. Тарау.
Фурье қатары үшін күшті қосындылау және
 класы.
класы.
1. 1. Көмекші леммалар . . .
1. 2. Негізгі теорема . . .
ІІ. Тарау. Күшті жуықтауға байланысты үзіліссіз модулі
2. 1. Фурье қатары үшін күшті қосындылау . . .
2. 2. Күшті жуықтауға байланысты үзіліссіздік модулі . . .
ІІІ. Қорытынды . . .
ІV. Пайдаланылған әдебиеттер
3
Кіріспе
Күшті қосындылау туралы түсінік.
Фейер теоремасы бойынша
 ұмтылған кезде
ұмтылған кезде
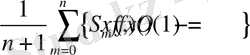 (1)
(1)
теңдігі орындалатын болса, онда
 класының кез келген
класының кез келген
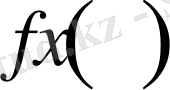 функциясы үшін
функциясы үшін
 .
.
Ең алғаш рет Хорди мен Литливуд барлық жерде
 (2)
(2)
теңдігінен күшті қатынас алуға бола ма деген сауал қойды.
Егер (2) қатынас кейбір х нүктелерінде орындалатын болса, онда қатар осы нүктеде күшті қосындыланады деп айтуға болады. Шартты түрде, қатар к көрсеткішті қосындыланады деп айтуға болады немесе кейбір ғалымдардың пайымдауынша
 (3)
(3)
теңдігін
 -қосындыланады деп айтуға болады.
-қосындыланады деп айтуға болады.
Егер
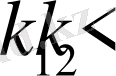 болса, онда Гельдер теңсіздігі бойынша
болса, онда Гельдер теңсіздігі бойынша
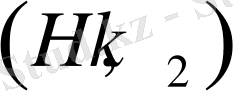 -қосындылауынан
-қосындылауынан
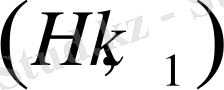 - қосындылауы келіп шығады, өйткені кез келген
- қосындылауы келіп шығады, өйткені кез келген
 үшін
үшін
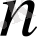
егер
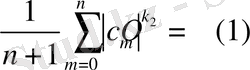

4 онда

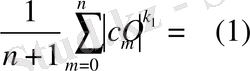
болады. Олай болса, (3) қатынастан күштірек к-дан үлкен нәтиже алуға болады.
Бұл дипломдық жұмыста Фурье қатарларын күшті қосындылау және оның үзіліссіздік модулімен арасындағы байланыс қарастырылады. Г. Фройд, Л. Лейндлер, И. Сабадош жұмыстарын зерттеудің жалғасы. Фурье қатары мен функциялар теориясындағы үзіліссіздік модулі мен ең жақсы жуықтаулар арасындағы байланыстар, Стечкин теңсіздігі, Гельдер теңсіздігі және тағы басқа теңсіздіктер қолданылады.
Енді керекті анықтамалар мен тұжырымдарды қарастырайық.
5
Анықтамалар мен керекті тұжырымдамалар
Анықтама1:
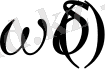 функциясы
функциясы
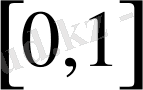 кесіндісінде үзіліссіз кемімейтін және төмендегі шарттарды қанағаттандыратын функция болсын.
кесіндісінде үзіліссіз кемімейтін және төмендегі шарттарды қанағаттандыратын функция болсын.
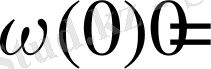 ,
,

мұндай функцияларды үзіліссіздік модулі деп атайды.
Анықтама2:
Айталық
 функциясы [a, b] анықталсын. Кез келген
функциясы [a, b] анықталсын. Кез келген


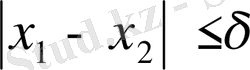

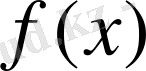 функциясының [a, b] кесіндісіндегі үзіліссіздік модулі дегеніміз
функциясының [a, b] кесіндісіндегі үзіліссіздік модулі дегеніміз
 .
.
Егер
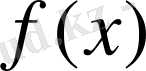 функциясына ешқандай шектеу қоймасақ, онда үзіліссіздік модулі
функциясына ешқандай шектеу қоймасақ, онда үзіліссіздік модулі
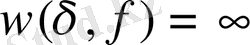 болуы мүмкін.
болуы мүмкін.
Егер
 болса, онда
болса, онда
 кез келген
кез келген
 үшін мына шарт орындалады:
үшін мына шарт орындалады:

Үзіліссіздік модулінің кейбір қасиеттерін келтірейік:
қасиет-
 .
.

қасиет-
 .
.
 монотонды өспелі
монотонды өспелі
қасиет-
 .
n-бүтін сан
.
n-бүтін сан
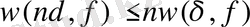 n=
n=
 кез келген оң сан
кез келген оң сан

қасиет-
 .
.
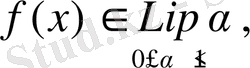 онда
онда
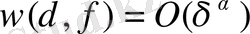
Анықтама3:
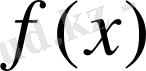
 класында жатады дейміз,
егер
класында жатады дейміз,
егер
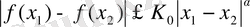 орындалса,
орындалса,
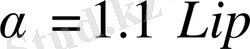
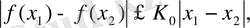
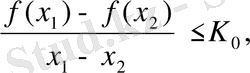
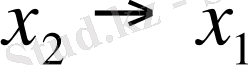
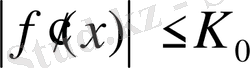
Дербес жағдайда 2
 периодты
периодты
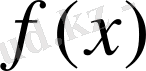 функциясының үзіліссіздік модулін былай жазуға болады.
функциясының үзіліссіздік модулін былай жазуға болады.
6
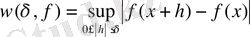
Анықтама4:
Мына
 ,
,
 функцияның ең жақсы жуықтауы тригонметриялық полиномның
функцияның ең жақсы жуықтауы тригонметриялық полиномның
 ретті
шамасы деп аталады
.
ретті
шамасы деп аталады
.
 функциясын реті
функциясын реті
 -нен аспайтын тригонометриялық полиноммен ең жақсы жуықтау дейміз.
-нен аспайтын тригонометриялық полиноммен ең жақсы жуықтау дейміз.
Ең жақсы жуықтаудың кейбір қарапайым қасиеттерін келтірейік:
Айталық
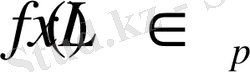
 болса, онда
болса, онда
1.
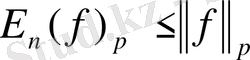
2.

3.

4.
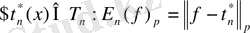
5. Егер
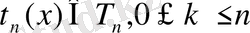 онда
онда
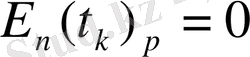
6.
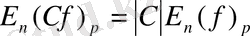 С-const
С-const
7.

8. Егер
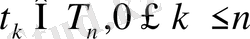 онда
онда
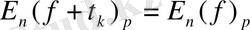
Теорема1: (Гельдер теңсіздігі)
Айталық
 -сандары өзара түйіндес
-сандары өзара түйіндес
 және
және
 функциялары
функциялары
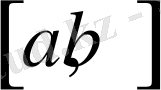 кесіндісінде бар болып, ақырлы болсын.
кесіндісінде бар болып, ақырлы болсын.
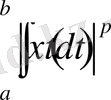 және
және
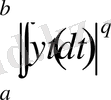 интегралдары бар болсын, онда
интегралдары бар болсын, онда
 функциялары да
функциялары да
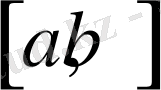 кесіндісінде интегралданады. Сөйтіп, мынадай теңсіздік орындалады.
кесіндісінде интегралданады. Сөйтіп, мынадай теңсіздік орындалады.
7
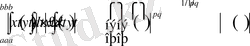
Бұл теңсіздік неміс ғалымы Гельдердің құрметіне Гельдер теңсіздігі деп аталады.
8
І тарау.
Фурье қатары үшін күшті қосындылау және
 класы.
класы.
- Көмекші леммалар
Лемма-1:
Егер
 өспелі емес, тізбегі оң және q>0 болса, онда
өспелі емес, тізбегі оң және q>0 болса, онда
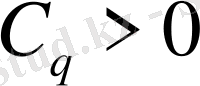 тұрақтысы бар болады және ол n-ге байланысты емес.
тұрақтысы бар болады және ол n-ге байланысты емес.
Олай болса
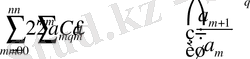 (n=1, 2, 3, …)
(n=1, 2, 3, …)
Дәлелдеуі:
Айталық
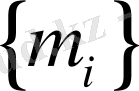 және
және
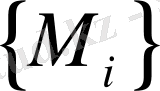 (i=1, 2, 3, …) екі натурал санының тізбегі сондай-ақ
(i=1, 2, 3, …) екі натурал санының тізбегі сондай-ақ
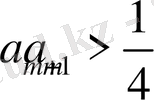 үшін
үшін
 (1. 1)
(1. 1)
және
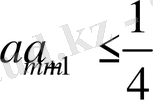 үшін
үшін
 (1. 2)
(1. 2)
болса, онда (2) -ден алатынымыз:
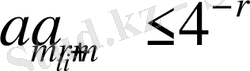
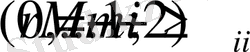
Сондықтан, егер
 болса, онда
болса, онда

сонымен бірге (1. 1) -ден
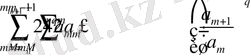
және осы соңғы екі теңдіктен
 үшін алатынымыз:
үшін алатынымыз:
9
 (1. 3)
(1. 3)
егер
 және
және
 болса, онда
болса, онда
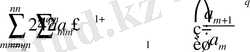 (1. 4)
(1. 4)
болады. Толығымен дәлелденді.
Сонымен, қорытындылай келе
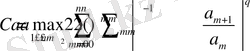
онда
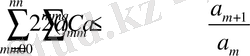
 үшін және (1. 3) , (1. 4) мәндері
үшін және (1. 3) , (1. 4) мәндері
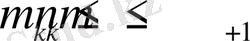 үшін. Сондықтан, біздің теңсіздігіміз дұрыс.
үшін. Сондықтан, біздің теңсіздігіміз дұрыс.
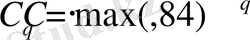
Лемма-1 толығымен дәлелденді.
Лемма-2:
Айталық
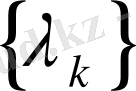 тізбегі және теоремадағы р бар болсын. Онда
тізбегі және теоремадағы р бар болсын. Онда
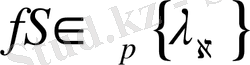 мәні
мәні
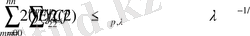 (1. 5)
(1. 5)
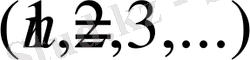
мұндағы
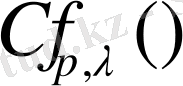 тұрақты оң және
тұрақты оң және
 нүктесіндегі f тригонметриялық полином үшін ең жақсы жуықтау.
нүктесіндегі f тригонметриялық полином үшін ең жақсы жуықтау.
10
Дәлелдеуі:
Алдымен
 болған жағдайды қарастырайық, онда Гельдердің теңсіздігін пайдаланып, мынаны аламыз:
болған жағдайды қарастырайық, онда Гельдердің теңсіздігін пайдаланып, мынаны аламыз:



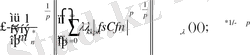
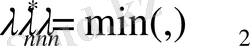
 үшін (1. 5) теңдік осыны береді.
үшін (1. 5) теңдік осыны береді.
Егер
 болса, онда [5] -тен келесі нәтиже қажет болады:
болса, онда [5] -тен келесі нәтиже қажет болады:
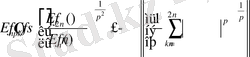
мұндағы
 , тек р-ға тәуелді. Осы теңсіздікті пайдалана отырып, 1-леммадан (1. 5) -ті аламыз.
, тек р-ға тәуелді. Осы теңсіздікті пайдалана отырып, 1-леммадан (1. 5) -ті аламыз.
Лемма-3:
Егер
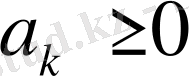 және
және
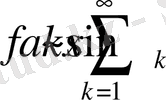 функциясы
функциясы
 класына тиісті болса, онда функция
класына тиісті болса, онда функция
11
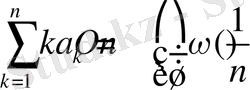
болады.
Дәлелдеуі:
Өйткені
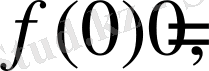
 тиісті, яғни
тиісті, яғни

сондықтан,

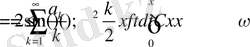
Егер
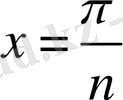 деп алсақ, онда
деп алсақ, онда
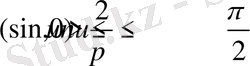

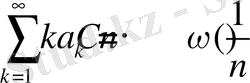
 үшін лемма-3 дәлелденді.
үшін лемма-3 дәлелденді.
Лемма-4:
Егер
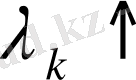 немесе
немесе
 және
және
 табылып,
табылып,
 сондай-ақ
сондай-ақ
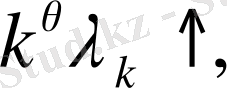 болса, онда
болса, онда
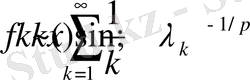 (1. 6)
(1. 6)
функциясы
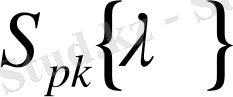 класына тиісті болады.
класына тиісті болады.
Дәлелдеуі:
Мына
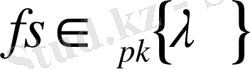 функцияның жинақталатының дәлелдейміз,
функцияның жинақталатының дәлелдейміз,
12
 және N нөмерін сондай бір
және N нөмерін сондай бір
 болатындай етіп таңдаймыз. Енді қатарды мына түрде қарастырамыз:
болатындай етіп таңдаймыз. Енді қатарды мына түрде қарастырамыз:

+


Алдымен
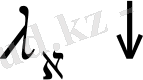 деп есептесек, кейбір
деп есептесек, кейбір
 үшін
үшін
 болады. Яғни,
болады. Яғни,
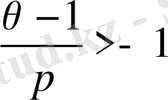 болады және бұдан шығатыны
болады және бұдан шығатыны

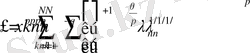
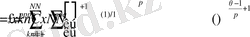


 сонымен қатар
сонымен қатар

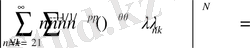
13
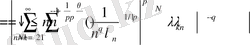



 жуықтау ретінен мынадай теңсіздік аламыз:
жуықтау ретінен мынадай теңсіздік аламыз:
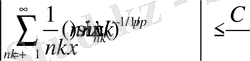
Сондықтан
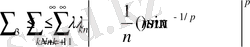
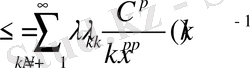

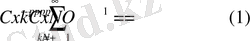
сондай-ақ
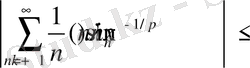

бұл
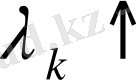 үшін дәлелденген, әйткенменде
үшін дәлелденген, әйткенменде
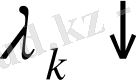 үшін де орынды делік. Біз байқағандай (1. 4) шарт
үшін де орынды делік. Біз байқағандай (1. 4) шарт
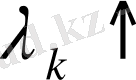 орындалады. Сондықтан біз толықтырулар қоспаймыз. Лемма-4 толығымен дәлелденді.
орындалады. Сондықтан біз толықтырулар қоспаймыз. Лемма-4 толығымен дәлелденді.
14
1. 2 Негізгі теорема
Айталық f функциясы
 периодты интегралданатын және
периодты интегралданатын және
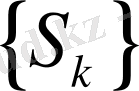 қосындының толық емес тізбегі. Осы функция үшін Фурье қатары бар болсын.
қосындының толық емес тізбегі. Осы функция үшін Фурье қатары бар болсын.
Фройд [1] дәлелдеуінде, егер
 және
және
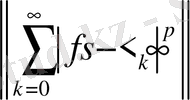 (1. 7)
(1. 7)
болса, онда
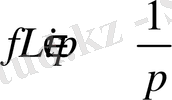 жатады.
жатады.
Лейндлер мен Никишиннің [3] жұмысында дәлелдегеніндей бұл (1. 7) шарт пен бірге p=1 болғанда
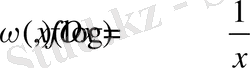
болатынын көрсеткен. Себебі

Осколков пен Сабадош дәлелдемелерінде яғни (1. 7) шарты мен қатар
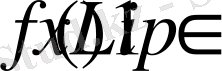 шарты қажетті.
шарты қажетті.
Лейндлер мен Никишин жұмысының нәтижесі Лейндлердің [4] жұмысында жалғасын тапқан. Яғни осы сұраққа жауап береді.
Бұл жұмыста мына мәселе тұрғысында қарастырылады, яғни
 монотонды тізбегі үшін қажетті және жеткілікті және сондай-ақ мына шарт орындалады.
монотонды тізбегі үшін қажетті және жеткілікті және сондай-ақ мына шарт орындалады.

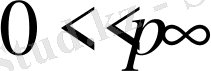
мұндағы
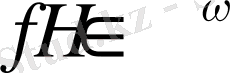 класында жатады,
класында жатады,
 үзіліссіз модуль бойынша тұрақты шама және
үзіліссіз модуль бойынша тұрақты шама және
 класындағы
класындағы
 функциясының
функциясының
 үзіліссіз модулі бар, яғни
үзіліссіз модулі бар, яғни

15

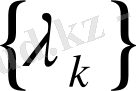 монотонды тізбек және
монотонды тізбек және
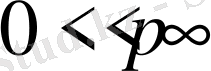 үшін келесі түрде көрсетеміз:
үшін келесі түрде көрсетеміз:

Енді келесі теореманы көрсетеміз:
Теорема:
Айталық
 дұрыс монотонды (кемімелі де, өспелі де емес) тізбек болсын. Сонымен қатар
дұрыс монотонды (кемімелі де, өспелі де емес) тізбек болсын. Сонымен қатар
 үзіліссіз модулі және
үзіліссіз модулі және
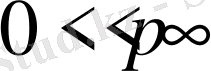 болса, онда
болса, онда
 шарты
шарты
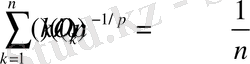 (1. 8)
(1. 8)
 (1. 9)
(1. 9)
қажетті.
 шарты
шарты
Егер
 мәні бар болса, сондай-ақ
мәні бар болса, сондай-ақ

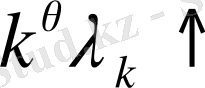 (1. 10)
(1. 10)
болса, онда кері жағдайда яғни (1. 8) шартқа (1. 9) шарт қажет.
Бұл теоремадан барлық нәтижелер ішінде көрсетілген және алдағы қарастырып кеткен сұраққа жауап аламыз. Сонымен қатар біздің бұл теорема Лейндлердің [2] жұмысының кейбір жерлерінде де кездеседі.
Дәлелдеуі:
 шарты
шарты
Егер
 болса, онда (1. 8) және (1. 5) қолданып, Стечкиннің келесі теңсіздігін пайдаланамыз:
болса, онда (1. 8) және (1. 5) қолданып, Стечкиннің келесі теңсіздігін пайдаланамыз:
16
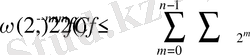
онда бұдан алатынымыз:
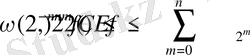

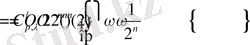
және
 класына тиісті.
класына тиісті.
 щарты
щарты
Егер (1. 8) шарт орындалмаса, онда 3-леммадан алынған функция
 -класы (1. 6) -ға қатысты емес, ал 4-леммадағы
-класы (1. 6) -ға қатысты емес, ал 4-леммадағы
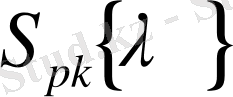 класына қатысты.
класына қатысты.
Теорема дәлелденді.
17
ІІ тарау. Күшті жуықтауға байланысты үзіліссіз модулі
- Фурье қатары үшін күшті қосындылау
Айталық
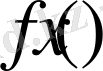 үзіліссіз,
үзіліссіз,
 периодты функция және оның фурье қатары
периодты функция және оның фурье қатары
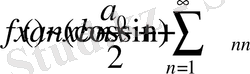 (1)
(1)
(1) -дің дербес n-ші ретті қосындысын
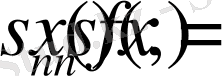 деп белгілейміз.
деп белгілейміз.
Күшті қосындылау жайында Фройдтың [1] жұмысында көрсетілген яғни барлық х-тар үшін қандай да бір f(x) функциясы келесі қасиетке ие болса,
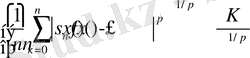 (2)
(2)
(мұндағы
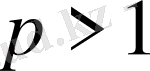 және К абсолютті тұрақты, )
және К абсолютті тұрақты, )
онда әрбір х үшін мына шарт орындалады.
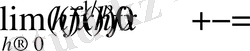 (3)
(3)
Фройдтың жұмысында мынадай мәселе қарастырылған. Барлық х үшін (3) шарты орындалады егер (2) шартты қанағаттандырса.
Біз бұл мәселеге толымсыз жауап бергенбіз, яғни (3) шартта х=0 болса, онда ол орындалмайды.
Біздің қарама- қарсы мысалымыздан:
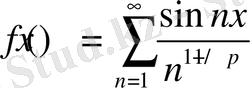
Енді бұл жұмыстан біз нәтижелерді талдап қорытындылаймыз.
Біз есептеген дұрыс қосындылау әдісі
 ұшбұрыштар матрицасы мен есептелінеді.
ұшбұрыштар матрицасы мен есептелінеді.
18

және
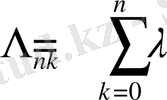 . Егер
. Егер
 ұмтылса, онда
ұмтылса, онда
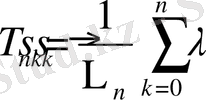
Айталық
 өспелі функция және n мен n+1 арасы сызықты дәл сондай-ақ
өспелі функция және n мен n+1 арасы сызықты дәл сондай-ақ
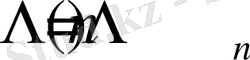 болсын.
болсын.
Теорема-1:
 Айталық
Айталық
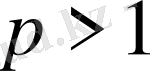 болсын. Бұл ұйғарым бойынша ұшбұрыштар матрицасы
болсын. Бұл ұйғарым бойынша ұшбұрыштар матрицасы
 келесі қасиетке ие болса, (
келесі қасиетке ие болса, (
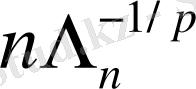 өседі)
өседі)
 (4)
(4)
 (5)
(5)
және
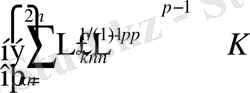 (6)
(6)
онда барлық х үшін
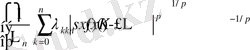 (7)
(7)
болса, онда
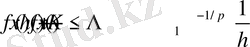 (8)
(8)
болады.
Сонымен бірге әрбір х үшін
19
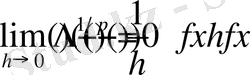 (9)
(9)
орындалады.
Біз (8) , (9) күшеймейтінің көрсете аламыз.
Дәлелдеуі : Былай деп есептесек
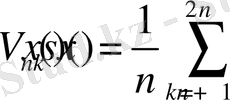 және
және
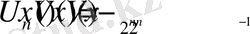
мұндағы
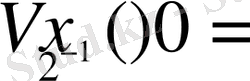 онда біз
онда біз
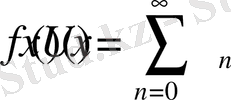 (10)
(10)
аламыз.
Өйткені

және (6), (7) -ден
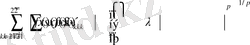
Бұдан алатынымыз:
 (11)
(11)
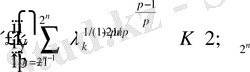
сондықтан, (10) және (5) , егер
 болса, онда алатынымыз:
болса, онда алатынымыз:
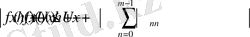
 (12)
(12)
20
Бізге белгілі Бернштейннің теңсіздігін пайдалансақ, онда (2. 2) және (2. 3) -тен алатынымыз:


(8) -теңсіздікті дәлелдедік. Енді біз (9) теңсіздікті дәлелдейміз. Дәлелдеу Фройдтың дәлелдеуіне ұқсас. Айталық
 кез келген оң сан . Егоровтың теоремасы және (7) -ден және
кез келген оң сан . Егоровтың теоремасы және (7) -ден және
 сондай-ақ
сондай-ақ
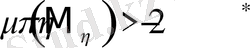 болсын. Бұл қатар
болсын. Бұл қатар
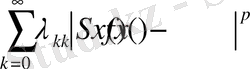 бірқалыпты жинақталады. Сондықтан (6) -дан алатынымыз, егер
бірқалыпты жинақталады. Сондықтан (6) -дан алатынымыз, егер
 және
және
 болса, онда
болса, онда
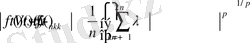 (14)
(14)
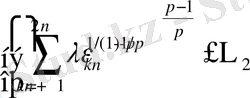
 таңдайық, сондай-ақ
таңдайық, сондай-ақ
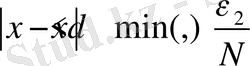 болсын. Айталық
болсын. Айталық
 ең аз натурал сан, сонымен қатар
ең аз натурал сан, сонымен қатар
 болсын.
болсын.
 үлкен, өйткені
үлкен, өйткені
 , яғни мұндағы
, яғни мұндағы
 нүктесі және х пен
нүктесі және х пен
 арасы сондай-ақ
арасы сондай-ақ
 болады. Бұдан (8) және (14) -тен шығатыны:
болады. Бұдан (8) және (14) -тен шығатыны:

21
 (15)
(15)

(5) -тен (15) -тің 1-ші мүшесін келесі түрде жазуға болады.

мұндағы
 және
және

 санының бүтін бөлігін көрсетеді.
санының бүтін бөлігін көрсетеді.
Енді (15) -тің 2-ші мүшесін (4) шартпен
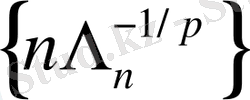 монотондық жүйесін пайдаланамыз: Егер
монотондық жүйесін пайдаланамыз: Егер
 болса, онда
болса, онда



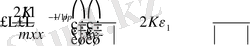
(15) -тің 3-ші мүшесін есептесек, онда біз мынаны аламыз:
22
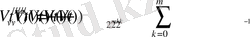
Сондықтан, Бернштейн теңсіздігін пайдалана отырып, (4) -шарттан және (11) есептеуден төмендегі бағалауға ие боламыз:

бұан шығатыны:

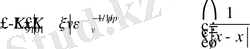
Жоғарыдағы қосындыдан алатынымыз:
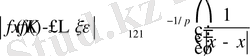 (16)
(16)
Өйткені барлық
 үшін (16) -ғы сияқты (9) -дың да туындысы бар болады.
үшін (16) -ғы сияқты (9) -дың да туындысы бар болады.
Айталық
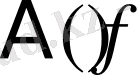 функциясы
функциясы
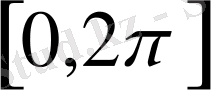 аралығында көрсетілген. Мұндағы (9) толық емес.
аралығында көрсетілген. Мұндағы (9) толық емес.
Шынында да
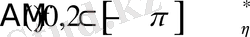 орынды.
орынды.
Сонымен қатар
 функциясының сыртқы өлшеуіші
функциясының сыртқы өлшеуіші
 -ға қарағанда кіші. Өйткені
-ға қарағанда кіші. Өйткені
 -ның туындысы бар.
-ның туындысы бар.
 өлшеуіші нөлге тең екені бізге белгілі, сонымен (9) -теңдік дәлелденді. Бұл жағдайда біз келесі теореманы аламыз.
өлшеуіші нөлге тең екені бізге белгілі, сонымен (9) -теңдік дәлелденді. Бұл жағдайда біз келесі теореманы аламыз.
Теорема-2:
Ұйғарым бойынша
 матрицасы теорема-1де сондай бір қасиетке ие болса, онда мынадай
матрицасы теорема-1де сондай бір қасиетке ие болса, онда мынадай
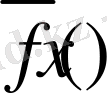 функция табылады және барлық х үшін мына шарт орындалады.
функция табылады және барлық х үшін мына шарт орындалады.
23
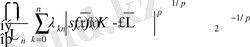 (17)
(17)
ал барлық
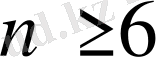 үшін
үшін
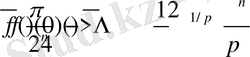 (18)
(18)
мұны тексеру қиын емес, мысалы мына жағдайда
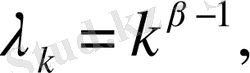


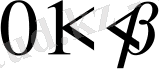
ал бұл (4), (5) және (6) шарттарды қанағаттандырады және
 матрицасы да дұрыс.
матрицасы да дұрыс.
Кейбір ескертулерде
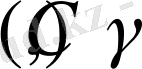 мәндері
мәндері

(мұндағы
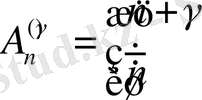 )
)
бұл теорема-1-гі орташа мән шартына тиісті емес. Егер
 болса, онда барлық х-тар үшін орынды.
болса, онда барлық х-тар үшін орынды.
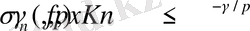 (19)
(19)
онда біз бұдан мына формуланы аламыз:
 (20)
(20)
және әрбір х үшін
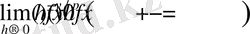 (21)
(21)
Ал бұл мына (19) шарттан келіп шығады.
24

егер біз
 деп есептесек, онда бұл шарт теорема-1-ді қанағаттандырады. Сонымен бұл теоремадан (20) және (21) теңдікті аламыз.
деп есептесек, онда бұл шарт теорема-1-ді қанағаттандырады. Сонымен бұл теоремадан (20) және (21) теңдікті аламыз.
Егер р=1 болса, онда біз осыған ұқсас теореманы көрсете аламыз.
Теорема-3:
Айталық ұшбұрыш матрицасы
 келесі қасиеттерден келіп шығады деп есептейік .
келесі қасиеттерден келіп шығады деп есептейік .
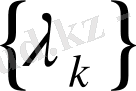 жүйесі оң және кемімелі болсын.
жүйесі оң және кемімелі болсын.

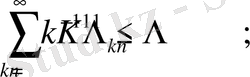 (22)
(22)
және
 онда егер барлық х үшін
онда егер барлық х үшін
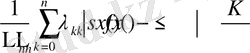
болса, онда бұдан шығатыны:
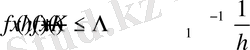
және әрбір х үшін мына бағалау орынды.
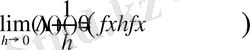
Сонымен қатар
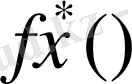 функциясы табылып және ол барлық х үшін мына қасиетке ие болсын.
функциясы табылып және ол барлық х үшін мына қасиетке ие болсын.

ал барлық
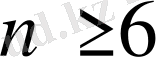 үшін
үшін
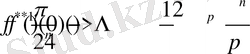
25
3-теореманың дәлелдеуінен 1және 2 теореманың нақты шешімі келіп шығады. Оған мысал ретінде
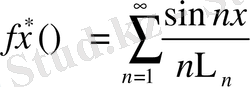
Бұны анықтау қиын емес, егер
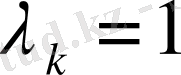 (к=1, 2, …) болса, онда (22) шарт орындалмайды. Сондықтан теорема-3-тен
(к=1, 2, …) болса, онда (22) шарт орындалмайды. Сондықтан теорема-3-тен
 орындалмайды, егер
орындалмайды, егер
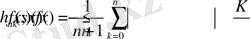
болса, онда келесі мысал
 шартында
шартында
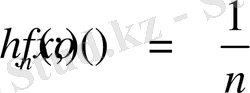 шарты шынымен де орындалмайды. Айталық
шарты шынымен де орындалмайды. Айталық
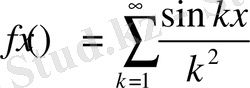 болсын. Бізге
болсын. Бізге
 екені белгілі, ал
екені белгілі, ал
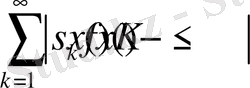
шарттан оңай есептеуге болады.
Шынымен де, егер
 болса, онда
болса, онда
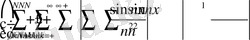
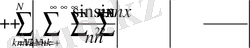
және бұл қосынды абсолют тұрақтыға қарағанда аз.
Дәлелдеуі: Айталық
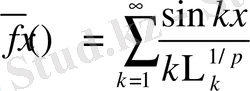
Біз 1-ші барлық х үшін бұл функцияның (17) қасиетке ие екенін көрсетеміз.
26
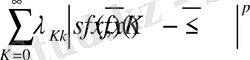 (23)
(23)
Егер x=0 болса, онда шынында да (23) орынды. Өйткені f(x) функциясы тақ, енді барлық оң х-тар үшін жеткілікті екенін тексеру керек. Айталық x(>0) кез келген тұрақты нүкте болсын. N нүктесін сондай бір мына
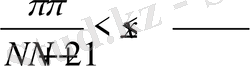 шартты қанағаттандыратындай етіп таңдаймыз. Осыдан біз (23) қосындыны 2- бөлікке бөлеміз:
шартты қанағаттандыратындай етіп таңдаймыз. Осыдан біз (23) қосындыны 2- бөлікке бөлеміз:
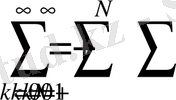 (24)
(24)
1-ші қосындыны оңай есептейміз:
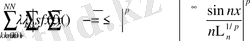
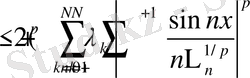
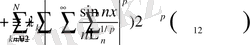
өйткені, (4) -тен
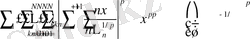
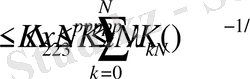
және
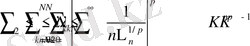
27
(24) -тің 1-ші қосындысы тепе-тең шектелген. (25) -тің 2-ші қосындысын есептесек, келесі түрде өзгереді.
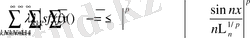

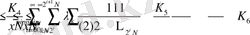
Көрсетілген нәтижеден алатынымыз,
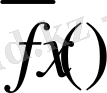 функциясы (17) теңдікті қанағаттандырады. (18) -ден алатынымыз
функциясы (17) теңдікті қанағаттандырады. (18) -ден алатынымыз
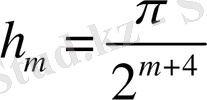 және
және
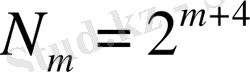 .
.
Егер
 болса, онда мына теңдікті аламыз:
болса, онда мына теңдікті аламыз:
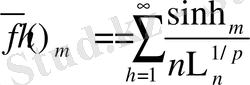
 (25)
(25)
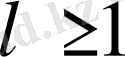 үшін түсінікті болғандай
үшін түсінікті болғандай

Сондықтан қосынды дұрыс болады.
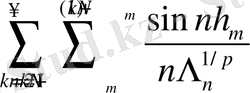
Сонымен қатар бұл оңай есептелінеді.
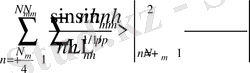
бұдан

және
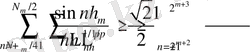
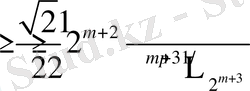


(25) -ті және нәтижені салыстыра отырып, мына бағалауды аламыз:

бұл
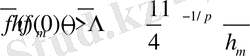
(18) -ге ұқсас дәлелденді. Сонымен теорема толығымен дәлелденді.
Бізге
 болғанда
болғанда
 жағдайы үшін
жағдайы үшін
 бағалауының орындалатындығы бұрынан жақсы белгілі, бірақ
бағалауының орындалатындығы бұрынан жақсы белгілі, бірақ
 жағдайы үшін бұл бағалау орындалмайды.
жағдайы үшін бұл бағалау орындалмайды.
Осыдан
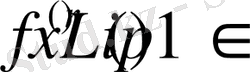 және
және
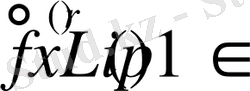 жағдайлары кез келген
жағдайлары кез келген
 оң мәні үшін төмендегі қатардың
оң мәні үшін төмендегі қатардың

дербес қосындысында анықтала ма деген заңды сұрақ тууы әбден ықтимал.
Бірқатар зерттеулер нәтижесінде бұл мәселенің орындалмайтындығы дәлелденді. Енді төмендегі теоремаларды дәлелдеуге көшейік.
Теорема -4:
тұрақты
 мәні үшін
мәні үшін
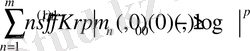 (26)
(26)
(2. 2) -теңсіздікті қанағаттандыратын
 функциясы және Lip1 класында жататын
функциясы және Lip1 класында жататын
 және
және
 функциялары табылады, мұндағы
функциялары табылады, мұндағы
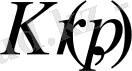 - және r және p-дан тәуелді тұрақты оң сан.
- және r және p-дан тәуелді тұрақты оң сан.
Бұл тұжырым төмендегі шарттың
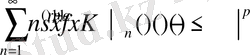
дербес жағдайынан туындаған.
Дәлелдеу. Айталық,
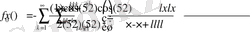
болсын. Ең алдымен
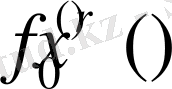 және
және
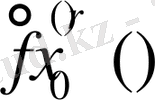 функциялары Lip1 класында жататындығын дәлелдейміз. Егер r жұп емес бүтін сан болса, онда
функциялары Lip1 класында жататындығын дәлелдейміз. Егер r жұп емес бүтін сан болса, онда
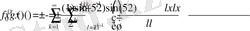
және

болады және егер r жұп болса, онда
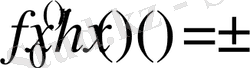 және
және
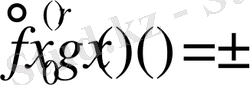
онда жоғарыдағы бағалаулардың орындары алмастырылады.
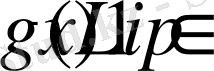 бағалауының орындалатындығы Лейндлердің [1] ғылыми тұжы-рымдамасында дәлелденген болатын, енді біз тек
бағалауының орындалатындығы Лейндлердің [1] ғылыми тұжы-рымдамасында дәлелденген болатын, енді біз тек
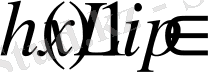 бағалауы да орындалатындығын көрсетеміз.
бағалауы да орындалатындығын көрсетеміз.
Егер
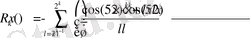
деп алсақ, онда
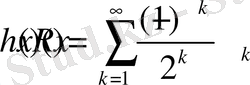
теңдігі орындалады.
Айталық, һ кез келген оң сан және
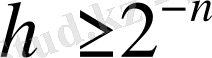 шартын қанағаттандыратын n жеткілікті кіші натурал сан болсын. Осы n натурал санының көмегімен һ(х) функциясын екі қосындыға бөліп жазуға болады
шартын қанағаттандыратын n жеткілікті кіші натурал сан болсын. Осы n натурал санының көмегімен һ(х) функциясын екі қосындыға бөліп жазуға болады
 .
.
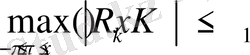 теңсіздігінен келесі бағалауға ие боламыз:
теңсіздігінен келесі бағалауға ие боламыз:
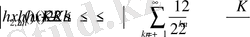 . (27)
. (27)
Енді біз барлық х-тер үшін
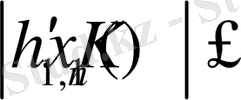
бағалауының орындалатындығына көз жеткіземіз. Қарапайым есептеулерден
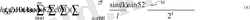
нәтижесіне ие боламыз.
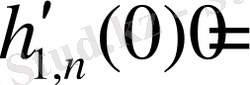 және
және
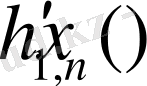 функциялары тақ болғандықтан
функциялары тақ болғандықтан
 аралығында
аралығында
 біркелкі жинақы екенін дәлелдесек жеткілікті. Айталық, m натурал саны
біркелкі жинақы екенін дәлелдесек жеткілікті. Айталық, m натурал саны
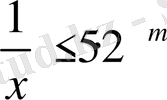 (28)
(28)
теңсіздігі орындалатындай өте аз шама және
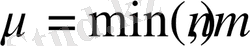 болсын. Сонымен
болсын. Сонымен
қатар,
 және
және
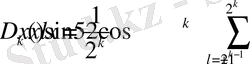 (29)
(29)
белгілеулерін енгізейік. Элементар есептеулерден
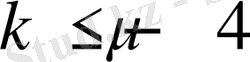 болса, онда
болса, онда
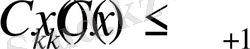 және
және
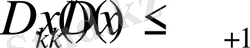 (30)
(30)
нәтижелеріне ие боламыз. Сондықтан (30) және (30) теңсіздіктерінен

және

бағалауларына ие боламыз, мұнда бізге белгілі төмендегі есептеулерді қолдану арқылы нәтиже алдық
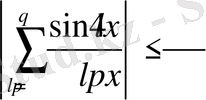 және
және
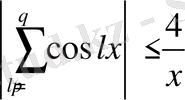 ,
,
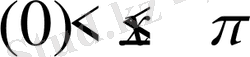 .
.
Алынған нәтижелерді жинақтай келе

бағалауының кез келген жағдайда орындалатындығына көз жеткіземіз. Осыдан және (11) -бағалаудан
 есептеуінің айқындылығы келіп шығады.
есептеуінің айқындылығы келіп шығады.
Енді (26) теңсіздікті дәлелдеуге көшейік. Егер р кез келген оң сан және
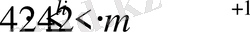 болса, онда
болса, онда
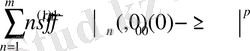

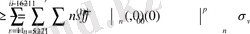 (31)
(31)
теңсіздігі орындалады.
Айталық,

болсын. Бұдан
 теңсіздігі орындалатындығы айқын көрініп тұр, сондықтан да
теңсіздігі орындалатындығы айқын көрініп тұр, сондықтан да
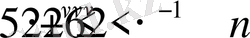 теңсіздігінен мына бағалаудың
теңсіздігінен мына бағалаудың

орындалатындығы келіп шығады, осы бағалаудан төмендегі нәтижеге ие боламыз:
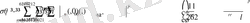
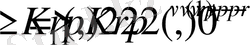 .
.
Соңғы бағалаудан және (2. 7) -теңсіздіктен 1-теоремадағы (2) -теңсіздік оңай дәлелденді.
Енді біз алынған теореманы одан сайын күшейте түсіп, талдау жасаймыз .
Теорема-5. Егер r теріс емес бүтін сан болса және барлық x-тер үшін
 (32)
(32)
қатары жинақталса, онда біз барлық х-тер мына бағалауға
 (33)
(33)
ие боламыз, сонымен қатар
 (34)
(34)
теңсіздігі де орындалады. (33) -бағалау тек
 үшін ғана емес,
үшін ғана емес,
 үшін орындалады.
үшін орындалады.
Егер r жұп болса, онда (32) -шарт үшін
 (35)
(35)
бағалауы орындалады, ал егер r бүтін тақ сан болса, онда
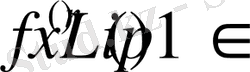 (36)
(36)
Сонымен қатар, бұл барлық х үшін
 (37)
(37)
шартын қанағаттандыратын
 функциясы табылады және r жұп бүтін сан болған жағдайда барлық
функциясы табылады және r жұп бүтін сан болған жағдайда барлық
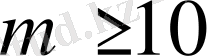 үшін
үшін
 (38)
(38)
 ,
,
 (39)
(39)
теңсіздіктерін аламыз, ал r бүтін тақ сан болған жағдайда
 және
және
 функциялары (38) және (39) -бағалауларында орын алмастырады.
функциялары (38) және (39) -бағалауларында орын алмастырады.
Дәлелдеуі: Ең алдымен (33) -теңдіктің орынды екенін дәлелдейік. Айталық,
 (n=1, 2…. )
(n=1, 2…. )
және
берілсін. Онда
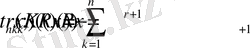

(39) теңдігі орындалады. (33) және (39) -бағалауларын қолдана отырып, келесі теңсіздікті

аламыз, осыдан
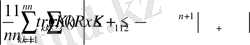
бағалауы келіп шығады. Бұл теңсіздік төмендегі қатардың
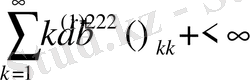
жинақы болатындығын көрсетеді және осыдан
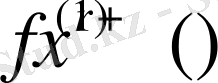 және
және
 квадраттық интегралданатын функция екендігі келіп шығады, сондықтан
квадраттық интегралданатын функция екендігі келіп шығады, сондықтан
 және
және
 абсолют үзіліссіз функциялар болып, (33) -теңдікке ие боламыз.
абсолют үзіліссіз функциялар болып, (33) -теңдікке ие боламыз.
Енді (34) -теңдікті дәлелдеуге көшейік. Төмендегідей белгілеулер енгізейік
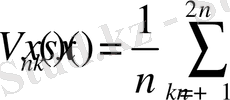 және
және
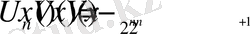 ,
,
мұндағы
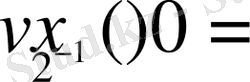 , олай болса
, олай болса

аламыз. Соңғы теңдіктің
 -ретті туындысы үшін төмендегі теңдікті дәлелдеу үшін
-ретті туындысы үшін төмендегі теңдікті дәлелдеу үшін
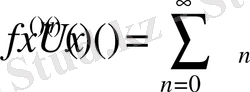 (40)
(40)
ең алдымен (17) -теңсіздіктің орындалатындығын тексерейік
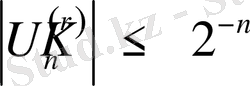 . (41)
. (41)
Енді төмендегі теңсіздікті

және (3) -теңсіздікті қолдана отырып

аламыз, бізге белгілі Бернштейннің теңсіздігінен қолдана отырып (41) -теңсіздікке ие боламыз. (41) -теңсіздік арқылы
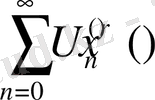
қатарының біркелкі жинақталатындығын көреміз және осыдан (40) -теңдіктің орындалатындығы келіп шығады. Егер
 болса, онда (40) және (41) -бағалаулардан
болса, онда (40) және (41) -бағалаулардан


теңсіздігіне ие боламыз, осыдан (10) -бағалау дәлелденді.
(35) және (36) дәлелдеу үшін Заманскийдің
 келесі нәтижесін қолда-
келесі нәтижесін қолда-
намыз:
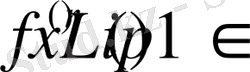 бағалауы тек қана r тақ үшін
бағалауы тек қана r тақ үшін
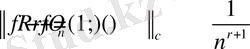 ,
,
r жұп үшін
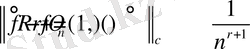
шартарын қанағаттандырғанда ғана орындалады, мұндағы
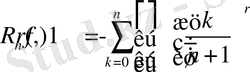
 .
.
Абел түрлендіруін пайдаланып
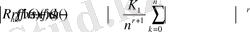
теңсіздігін оңай есептейміз, осыдан және (8) -теңсіздіктен Заманскийдің белгілі нәтижесі арқылы (35) және (36) -формулалардың айқындылығы келіп шығады.
(37), (38) және (38) -функцияларының қасиетінен төмендегі өте қарапайым формулаға ие боламыз
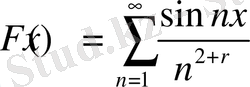 . (42)
. (42)
(8) -теңсіздіктің дұрыстығын тексеру үшін N натурал санын бір
 теңсіздігі орындалатындай етіп таңдаймыз. Онда
теңсіздігі орындалатындай етіп таңдаймыз. Онда
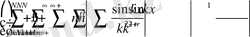
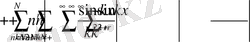
болады. Мұндағы қосындылар - абсолют тұрақтыдан аз шама, атап айтқанда
 ,
,
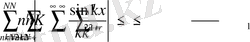 ,
,
Осыдан бізге жақсы белгілі

бағалауын пайдалана отырып
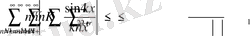
теңсіздігін аламыз.
Енді келесі лемманы дәлелдейік.
Лемма.
Айталық,
 тізбегі төмендегі теңсіздікті
тізбегі төмендегі теңсіздікті
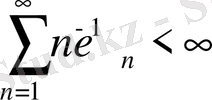
қанағаттандырытын кемімелі сандық тізбек және

болсын. Онда кез келген
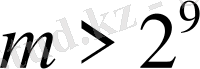 саны үшін
саны үшін
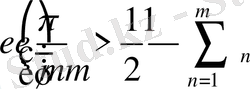 .
.
Дәлелдеу.
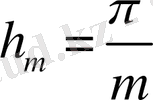 белгілеуін енгізейік. Осыдан
белгілеуін енгізейік. Осыдан
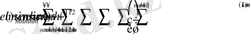 (43)
(43)
аламыз. Кез келген
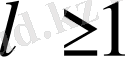 үшін
үшін

бағалауының орындалатындығы ақиқат, сондықтан келесі қосынды

оң мәнге ие болады. Енді келесі бағалаудың орындалатындығын көреміз
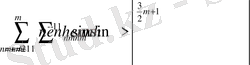 . (44)
. (44)
Осы теңсіздіктен
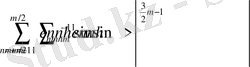
және
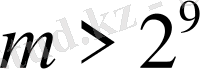 жағдайы үшін
жағдайы үшін

бағалауын аламыз, осыдан (44) -теңсіздік дәлелденеді.
Алынған нәтижелерді жинақтай келе (41) -бағалау арқылы лемманың есебіне байланысты төмендегі бағалауды аламыз
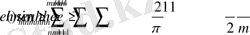 .
.
Осы лемманы пайдалана отырып (37) бен (38) -бағалауларды оңай дәлелдей аламыз. Егер r жұп болса, онда
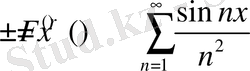
және
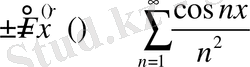
орындалатындығы ақиқат. (14) -бағалау лемма арқылы оңай анықталады және осыдан
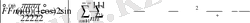
(37) -бағалау да дәлелденеді.
Егер r тақ болса, онда (38) және (39) бағалаулар дәл осыған ұқсас дәлелденеді.
30
2. 3 Күшті жуықтауға байланысты үзіліссіздік модулі
Айталық
 функциясы
функциясы
 -периодты интегралданатын функция және оның Фурье қатары
-периодты интегралданатын функция және оның Фурье қатары
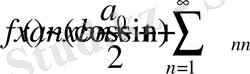 (1)
(1)
болсын.
Бұл функция үшін фурье қатарының
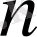 -ші дербес қосындысы
-ші дербес қосындысы
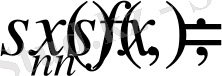 деп белгілейміз және оның
деп белгілейміз және оның
 нормасы бар.
нормасы бар.
Егер
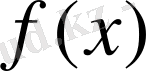 мына қасиетке ие болса
мына қасиетке ие болса
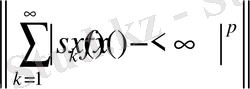 , p>1
, p>1
үшін онда
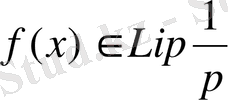
және
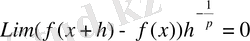
болады және ол барлық уақытта орындалады. Бұл Фройдтың [2] дәлелденген.
Дәл сол сияқты p=1 болғанда Лейндлер мен Никишин [4] -да зерттеген және олардың нәтижелері Лейндлердің [3] -да талданған. Бұдан келіп шығатыны, егер r теріс емес, бүтін сан болса сонымен бірге
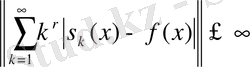
болса, онда
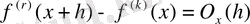
барлық х үшін орынды және

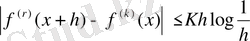
болады. Бұл жуықтау жалпы тиімді мүмкіндік. Осы нәтижеден келесіні аламыз:

бұл
 класына тиісті емес. Осыдан Лейндлер былай деп сұрақ қойады:
класына тиісті емес. Осыдан Лейндлер былай деп сұрақ қойады:
Егер
 0<p<1
0<p<1
болғанда
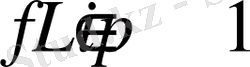 шарты орындала ма?
шарты орындала ма?
Осколков пен Сабадош бұл сұрақтың орынды екенін көрсетті. Олар бұл сұраққа жалпыланған түрде жауап берді. Яғни, егер
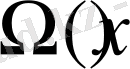 -кез келген үзіліссіздік модулі үшін
-кез келген үзіліссіздік модулі үшін
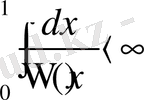 болса және
болса және
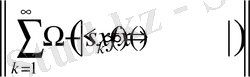

жататының көрсетеді.
Бұл шартты жинақтылыққа зерттейтін болсақ, айталық
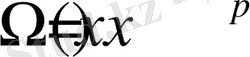 болсын. (мұндағы 0<p<1 p
болсын. (мұндағы 0<p<1 p
 1)
1)
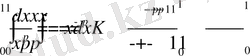 (мұнда p<1, 0<1-p) (K-const)
(мұнда p<1, 0<1-p) (K-const)
яғни бұдан біз
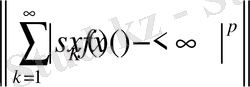
жинақталатының көреміз.
Бұдан шығатыны
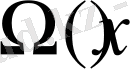 - әрқашан өспелі функция, дөңес немесе ойыс мәнге ие болса, онда
- әрқашан өспелі функция, дөңес немесе ойыс мәнге ие болса, онда
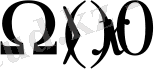 (x>0),
(x>0),
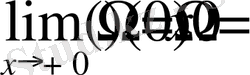
сонымен
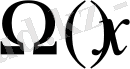 -тің кері мәні бар деп есептеп, оны
-тің кері мәні бар деп есептеп, оны
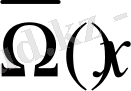 деп белгілейміз және ол
деп белгілейміз және ол
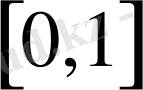 аралығында жатады.
аралығында жатады.
 -ті
-ті
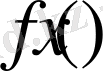 -тің үзіліссіздік модулі деп белгілейміз.
-тің үзіліссіздік модулі деп белгілейміз.
Теорема:
Егер
 - үзіліссіз функция дөңес немесе ойыс және егер
- үзіліссіз функция дөңес немесе ойыс және егер
 , (2)
, (2)
онда
 (3)
(3)
мұндағы
 -функциясы
-функциясы
 -ның кері функциясы.
-ның кері функциясы.
Мына теңсіздік үшін
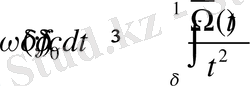 , (c>0)
, (c>0)
 (4)
(4)
(1) шартты қанағаттандыратын
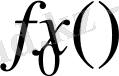 функциясы табылады.
функциясы табылады.
, (c>0)
Егер
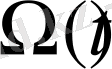 ойыс болса, онда
ойыс болса, онда
 -ды
-ды
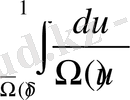 -ға алмастыруға болады.
-ға алмастыруға болады.
Бұдан шығатыны, егер
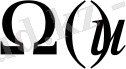 үзіліссіздік модулі түріндегі функция болса, (1) шарттын
үзіліссіздік модулі түріндегі функция болса, (1) шарттын
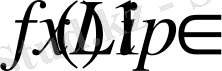 класында жататындығы мына шарт үшін
класында жататындығы мына шарт үшін
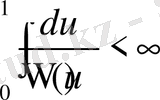 (5)
(5)
қажетті және жеткілікті.
Салдар:
Егер
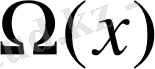 -тің кез келген үзіліссіз модулі бар болса, онда
-тің кез келген үзіліссіз модулі бар болса, онда
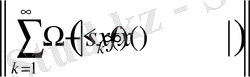
шарт

 мәніне ие болады тек қана сонда ған егер
мәніне ие болады тек қана сонда ған егер

шарт орындалса.
Салдар теоремадан келіп шығады, өйткені егер
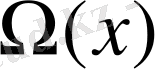 -тің үзіліссіз модулі бар болса, онда біз мына жағдайда
-тің үзіліссіз модулі бар болса, онда біз мына жағдайда
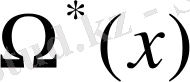 ойыс функцияны таба аламыз:
ойыс функцияны таба аламыз:
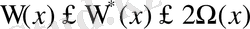
Теореманы дәлелдеу үшін бізге келесі 3- леммалар керек болады.
Лемма-1
: Егер
 функциясы ойыс және (5) шартты қанағаттандыратын болса, онда
функциясы ойыс және (5) шартты қанағаттандыратын болса, онда
болады.
Лемма-2:
Айталық
 кемімелі сандар тізбегі болсын және
кемімелі сандар тізбегі болсын және
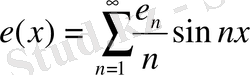
болса, онда
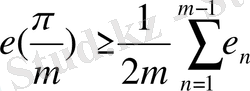
Лемма-2 Лейндлердің құрметіне негізделген.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz