Туынды, дифференциалдық теңдеулер және механиканың негізгі ұғымдары
Кіріспе
XXI ғасырды - ақпарат және дамыған техника заманы дейді. Сондықтан студенттер математикалық аппаратты түсініп және оны қажетінше меңгеруде. Классикалық механика заңдарын білу өте қажетті. Осы заңдар негізінде жаңа машиналар жасау және сол машыналарды жасауда пайдаланатын құрал жабдықтарды дамытуда қозғалыс ұғымы өте маңызды. Өйткені барлық машиналар және құрал жабдықтар қозғалатын бөлшектерден тұрады. Олардың барлығы бізді қоршаған кеңістікте әйтеуір бір қозғалыс джасайды. Осы қозғалыстардың барлығының өздеріне тиесілі заңдары бар. Ол заңдар математикалық өрнектер арқылы жазылып зерттеледі. Нүкте және дене қозғалысының заңы бойынша машиналарды бөлшектерінің қозғалыстарын зерттейміз. Осы зерттеулер нәтижесінде қажетті бөлшектер жасал ып өңделеді.
Дүниедегі барлық болып жатқан біз білмейтін құбылыстар, олар қандай да қиын болдса да барлығы материяның түрлері мен қасиеттері. Ал материяның бар болуы негізгі түрі - ол қозғалыс. Материя бір түрден екінші бір басқа түрге өте алады. Механикада біз тек оның заттық түрлерінің ғана қарастырамыз. Өйткені барлық жасайтын машиналар мен құрал жабдықтар тек заттардан ғана тұрады.
1. Туынды ұғымы және дифференциялдық теңдеулер.
1. 1. Туынды және дифференциал ұғымы.
Бір Х аралығында
\[y=f(x)\]
функциясы анықталатын осы аралықта жататын кез келген
\[x\in X\]
нүктесін алып х аргументіне
\[X_{0}\]
нүктесінде
\[\Delta x\]
өсімшесін берейік және
\[x_{0}\,+\,\Delta x\]
сол Х аралығында жататындай. Сонда функция мәні
\[y=f(x_{0}\,+\,\Delta x)\]
(1. 1. 1. ) болады және оның өсімшесі
\[y=f(x_{0}+x)-f(x_{0})\]
(1. 1. 2. ) тең болады. Табылған
\[\Delta y\]
функция өсімшесінің
\[\Delta x\]
аргумент өсімшесіне қатынасын тауып, оның
\[\scriptstyle{\mathrm{br}}\quad\scriptstyle{\mathrm{or}}\quad\scriptstyle{\mathrm{o}}\]
нөлге ұмтылғандағы шегін табайық.
\[\operatorname*{lim}_{\operatorname{heo}0}\;\;{\frac{\mathbf{D}y}{\mathbf{D}x}}=\operatorname*{lim}_{\mathbf{hei}}{\frac{f(x_{0}+\mathbf{D}x)-\;f(x_{0})}{\Delta x}}\]
(1. 1. 3. )
Егер осы (1. 1. 3. ) өрнектің үшегі бар және ол ақырлы болса, онда оны
\[y=f(x)\]
функциясының нүктесіндегі туындысы деп атайды және былай белгіленеді:
\[f^{\prime}(x_{0})=\operatorname*{lim}_{\mathrm{{Dx}}}{\frac{f(x_{0}+\mathbf{D}x)-\,f(x_{0})^{\prime}}{\Delta x}}\]
(1. 1. 4. )
Мысал1. 1. 1.
\[y=f(x)=x^{3}\]
функциясының
\[x=x_{0}\]
нүктесіндегі туындысын табу қажет.
Шешуі.
х - қа
\[\Delta x\]
өсімшесін береміз. Сөйтіп функцияның
\[\Delta y\]
өсімшесін табайық.
\[\mathrm{D}y=f(x_{0}+\mathrm{D}x)-\ f(x_{0})={(x_{0}+\mathrm{D}x)^{3}}-\ x_{0}{}^{3}=\]
\[x_{0}^{~3}+3x_{0}^{~3}\mathrm{D}x+3x_{0}\mathrm{D}x^{3}+\mathrm{D}x^{3}-\,x_{0}^{~3}=3x_{0}^{~2}\mathrm{D}x+3x_{0}\mathrm{D}x^{2}+\Delta x^{3}\]
\[\scriptstyle{\mathrm{br}}\quad\scriptstyle{\mathrm{d}}\]
ұмтылғандағы шегін табайық.
\[\operatorname*{lim}_{\Delta\Phi\ 0}\;\;\;\;{\frac{{\mathrm{D}}y}{{\mathrm{D}}x}}=\operatorname*{lim}_{\mathrm{tare}}{\frac{3x_{0}^{2}\,{\mathrm{D}}x+3x_{0}{\mathrm{D}}x^{2}+{\mathrm{D}}x^{3}}{{\mathrm{D}}x}}=\]
\[\operatorname*{lim}_{\operatorname{Dxo}}3x_{0}^{2}+\operatorname*{lim}_{\operatorname{Dxo}}3x_{0}\mathbf{D}x+\mathbf{D}x^{2}=3x_{0}^{2}\]
Осыдан
\[f^{\prime}(x_{0})=3x_{0}^{~2}\]
болады.
1. 1. 1. Туындының геометриялық мағынасы.
Бізге (а, в) аралығында
\[y=f(x)\]
анықталып графигімен берілсін
\[\Delta{\tilde{G}}\]
\[y=f(x)\]
\[\Delta\vec{\sigma}\]
\[\phi\left(\Delta x\right)\]
\[{\mathcal{X}}_{0}\]
1. Сурет
М - нүктесі графикте
\[X_{0}\]
мәні сай болсын. Сонда
\[{\tilde{O}}_{0}+\Delta x\]
мәніне сәйкес мәні N - болсын (MN) түзуін жүргізейік. Ол түзу ОХ өсінен құрған бұрысты ОХөсінен құрған бұрысты
\[\phi\left(\Delta{\tilde{O}}\right)\]
деп белгілейік. Егер
\[\mathrm{br}\ ^{\prime}\]
ұмтылғанда
\[{\cal N}\hookrightarrow\ {\cal M}\]
ұмтылып (MN) түзуі (МК) түзуімен беттеседі.
(МК) түзуінің ОХ өсімен құрған бқрыш
\[\phi_{_0}\]
тең болады. Ол
\[\Delta h V H S\]
үшбұрышының
\[{\mathcal{L}}N M P\]
- бұрышы
\[\phi\left(\Delta x\right)\]
бұрышына тең.
Сонда
\[{\tilde{l}}_{\otimes}^{\mathcal{O}}\]
\[\phi(\mathbf{D}x)={\frac{(\mathbf{D}y)}{(\Delta x)}}\]
(1. 1. 1. 1. ) осыдан
\[\operatorname*{lim}_{\mathrm{baeo}}t g(\mathbf{D}x)=\operatorname*{lim}_{\mathrm{D}y}{\frac{\mathbf{D}x}{\mathbf{D}y}}=t g\phi_{\mathrm{0}}\]
(1. 1. 1. 2. ) шығады. Сонда
\[f^{\prime}\left(x_{0}\right)=t g\phi_{0}\]
(1. 1. 1. 3. ) болады. Ол дегеніміз туындының геометриялық мағынасы берілген нүктеден жүргізілген жанаманың ОХ өсінен құрайтын бұрышының таненсы яғни жанамалық бұрыштың коэффициенті.
1. 1. 2. Туындының механикалық мағынасы.
Бізге бір Т аралығында
\[{\widehat{\theta}}\ =S(t)\]
функциясы анықталсын.
\[\frac{d}{\beta}\]
аргументіне
\[\Delta t\]
өсімше берсек функция өсімшесі
\[\textstyle\mathbf{D}S(t)=S(t+\mathbf{D}t)-S(t)\]
болады.
\[{\mathbf{}}S(t)\]
- нүктенің қозғалыс заңы десек, ал
\[\frac{d}{\beta}\]
уақыт деп алсақ, онда
\[\Delta t\]
- уақытта нүкте
\[\Delta S(t)\]
жол жүреді. Жолдың уақытқа қатынасы
\[{\frac{\mathrm{D}S(t)}{\mathrm{D}t}}=V_{i0}\]
(1. 1. 2. 1. )
Физикадан
Орташа жылдамдыққа тең. Осыдан
\[{\bf S}^{\prime}(t)\operatorname*{lim}_{\mathrm{D}^{\rightarrow}0}{\frac{\mathrm{DS}(t)}{\mathrm{D}t}}=V_{\hat{e}\hat{a}_{\zeta}}\]
(1. 1. 2. 3. ) ' Туынды
\[\frac{d}{\beta}\]
уақытындағы
\[\textstyle\sqrt{\underline{{\theta}}}_{\dot{\alpha}\dot{\alpha}_{\zeta}}\]
- Лездің жылдамдыққа тең болады. Функцияның бірінші туындысы, оның өзгеруінің жылдамдығына тең болады. Осы туыныдының механикалық мағынасы болады.
1. 1. 3. Дифференциял ұғымы.
Функцияның нүктеде дифференциялдану шарты былай беріледі. Егер функцияның өсімшесін
\[\mathrm{I}{\mathcal{I}}=A\mathrm{I}{\mathfrak{M}}+\lambda\left(\mathrm{I}{\tilde{\mathcal{O}}}\right)\Delta{\tilde{\mathcal{O}}}\]
(1. 1. 3. 1. ) түріндегі өрнекпен беруге болатын болса, онда ол функция х нүктесінде дифференциялданады дейді.
Мұнда А -
\[\Delta\vec{\sigma}\]
тәуелді емес бір тұрақты, ол
\[{\mathcal{A}}\left(\Delta{\widetilde{O}}\right)\]
-
\[\Delta\vec{\sigma}\]
тәуелді ақырсыз кіші шама және оның
\[{\mathsf{D}}{\bar{\mathcal{O}}}\hookrightarrow0\]
ұмтылғанда оданда бұрын нөлге ұмтылады.
\[\operatorname*{lim}_{0}\]
\[{\mathcal{N}}\left(\Delta{\widetilde{\mathcal{D}}}\right)\]
=0 (1. 1. 3. 2. ) Осыдан
\[\operatorname*{lim}_{\mathrm{Dte}\,\atop\bf{D B}}\frac{{\bf{D}}}{{\bf{D}}\vec{\sigma}}=\operatorname*{lim}_{\bf{D}^{\prime}\rightarrow\,\vec{\nabla}}\frac{A{\bf{D}}\vec{\sigma}+\lambda\,({\bf{D}}\vec{\sigma}){\bf{D}}\vec{\sigma}}{{\bf{D}}\vec{\sigma}}=\hat{A}\]
яғни (1. 1. 3. 2. ) Яғни
\[f^{\prime}(x)=\dot{A}\]
(1. 1. 3. 3. ) Осыдан
\[\mathbf{D}\theta=\textstyle{\int}^{\prime}(x)\mathbf{D}{\bar{\theta}}+\lambda\ (\mathbf{D}{\bar{\theta}})\Delta{\tilde{\theta}}\]
(1. 1. 3. 4. ) деп алуға болады.
Анықтама1. 1. 3. 1.
\[y=f(x)\]
функциясының дифференциялы деп, оның өсімшесінің
\[\Delta\vec{\sigma}\]
қатысты сызықты бас бөлігінайтады.
\[\mathbf{D}\theta=\textstyle{\int}^{\prime}(x)\mathbf{D}{\boldsymbol{\tilde{o}}}+\lambda\,(\mathbf{D}{\boldsymbol{\tilde{o}}})\Delta{\tilde{o}}\]
(1. 1. 3. 5. ) оның сызықты бас бөлігі
\[d y\]
деп белгіленеді және ол
\[d\theta=f^{\prime}\,(x)\Delta\bar{\theta}\]
(1. 1. 3. 6. ) Мұнда х - тәуелсіз айнымалы болғандықтан, оның өсімшесі дифференциялдануы тең
\[\mathrm{D}{\bar{\theta}}=d x\]
\[d\theta=f^{\prime}\left(x\right)d\tilde{\sigma}\]
(1. 1. 3. 5. ) (1. 1. 3. 6. ) өрнектен
\[f^{\prime}(x)={\frac{d y}{d x}}\]
(1. 1. 3. 7. )
1. 2. Дифференциял теңдеулер.
1. 2. 1. Бірінші ретті дифференциял теңдеулер.
1. 2. 1. 1. Жалпы ұғымдар бар болу теоремасы.
Бір айнымалы функцияның интегралын есептеуде біз белгісіз
\[\mathcal{E}\]
функциясын оның туыныдысы немесе дифференциялы арқылы табу есептерін қарастырғанбыз, яғни
\[\vartheta^{\prime}=f(x)\]
немесе
\[d y=f(x)d x\]
(1. 2. 1. 1. 1. ) мұнда
\[\mathcal{E}\]
белгісіз функция
\[f\left(\,x\,\right)\]
беріл ген
\[\widetilde{{\cal O}}\]
- қа қатысты функция, сонда бұл (1. 2. 1. 1. 1. ) қарапайым дифференциял теңдеу болады. Бұл теңдеуді шешу үшін біз
\[\widetilde{{\cal O}}\]
- қа тәуелсіз белгісіз
\[\mathcal{E}\]
функциясын табуымыз керек, ол үшін берілген
\[f(\,x\,)\]
функциясын интегралдауымыз қажет болады. Ондай жағдайда біз шексіз көп бір бірінен тек тұрақты
\[\Lambda{\tilde{V}}\]
- ға айырмалы болатын функцияларды табамыз. Егер
\[\textstyle\int(x)d x\]
- ты алғашқы функциясы деп ұйғарсақ, онда (1. 2. 1. 1. 1. ) кез келген шешуі мына түрде жазылады
\[\vartheta=\ \ j(x)d x+\bar{N}\]
(1. 2. 1. 1. 2. )
Бірақта кейінірек біз (1. 2. 1. 1. 1. ) - ден күрделі түрдегі теңдеулермен кездесеміз Ол теңдеулерде
\[{\mathcal{O}}^{j}\]
- туындыдан басқа
\[\mathcal{E}\]
- өзіде кіреді.
Мысал1. 2. 1. 1. 1.
\[{\mathcal O}^{\prime}\,+\,\tilde{\mathcal O}^{2}\,\mathcal O=0\]
\[\theta^{\prime}=\frac{\check{\sigma}}{\check{\sigma}}\]
т. б.
Анықтама1. 2. 1. 1. 1.
Бірінші ретті ди фференциял теңдеу деп біз тәуелсіз айнымалының белгісіз функциясын және оның туындысын байланыстыратын теңдеулерді айтамыз.
Бірінші ретті дифференциял теңдеулер жалпы түрде былай беріледі:
\[F(x,y,y^{\prime})=0\]
(1. 2. 1. 1. 3. ) ол дербес жағдайларда (1. 2. 1. 1. 3. ) теңдеудің сол жағында
\[\widetilde{{\cal O}}\]
және
\[\mathcal{E}\]
кірмейді, ал
\[{\mathcal{O}}^{j}\]
міндетті түрде болады. Бұл жағдайда теңдеу былай беріледі:
\[{\mathcal O}^{\prime}\equiv\mathcal{J}(\chi,y)\]
(1. 2. 1. 1. 4. )
Анықтама 1. 2. 1. 1. 2.
(1. 2. 1. 1. 3. ) немесе (1. 2. 1. 1. 4. ) дифференциялдық теңдеудің шешімі деп: осы теңдеуге қойғанда оны тепе - теңдікке айналдыратын белгісіз функцияны айтады.
Жоғарыда көрсеткендей (1. 2. 1. 1. 1. ) теңдеудің шексіз көп шешімі болатынын айтып және олар бір бірінен тек С - тұрақтыға айырмалы болады дейік. Сонда осы шешімдер жиыны берілген (1. 2. 1. 1. 1., 1. 2. 1. 1. 2., 1. 2. 1. 1. 3. ) дифференциялдық теңдеудің жалпы шешімі дейді және былай белгілейді:
\[y=\phi\left(x,c\right)\]
(1. 2. 1. 1. 5. )
Осы (1. 2. 1. 1. 5, С - 4 орнына сан мәні берілсе онда оны дифференциялдық теңдеудің шешімі дейді.
Кейінірек біз нақты есепті шешкенде көбінде біз дербес шешімін табуды қажет деп табамыз. Сондықтан (1. 2. 1. 1. 5. ) біз тұрақты С бір берілген есеп сәйкес нақты мәнін табуымыз қажет. Ол үшін есептеп басқа тағы бір шарт берілуі керек. Ол шартты есептің бастапқы шарты деп, мына түрде береді
\[{\hat{O}}\ {\overline{{\theta}}}_{\overline{{{\theta}}}_{0}}={\hat{O}}_{0}\]
(1. 2. 1. 1. 5)
Мысал1. 2. 1. 1. 2.
Жоғарыда біз
\[\theta^{\prime}=\frac{\check{\sigma}}{\check{\sigma}}\]
есепті мысал ретінде бергенбіз.
Бұл дифференциялдық теңдеудің жалпы шешімі
\[\textstyle{\mathcal{O}}=N{\tilde{\mathcal{O}}}\]
болады. Енді бір б астапқы шарт берейік
\[{\cal O}\vert_{\partial=2}=6\]
деген
\[\delta=2,y=6\]
деген мәнді.
Жалпы шешімге қойсақ
\[\scriptstyle6=2C\]
деген те ңдеу шығады. Осыдан
\[C=3\]
болады.
С - тұрақтының осы мәнін жалпы шешісге қойсақ
\[y=3x\]
деген дербес шешімін табамыз.
Шешімнің бар болуы және ол жалғыз екені туралы теорема
Егер
\[{\mathcal{S}}\left(\mathcal{N}_{9}\setminus\mathcal{Y}\right)\]
функциясы
\[\textstyle P_{0}\left(\mathcal{X}_{0}\,\mathcal{Y}_{0}\right)\]
нүктесі н бар облысты үзіліссіз болса, онда
\[{\mathcal O}^{\prime}\equiv\mathcal{J}(\chi,y)\]
теңдеуді
\[{\tilde{O}}(x_{0})=y_{0}\]
болғанда
\[\bar{\theta}=\bar{\theta}(\tilde{\theta})\]
деген шешімі болады. Оның үстіне
\[\frac{\mathbb{H}\ell}{\partial y}\]
дербес туынды үзіліссіз болса, онда ол шешім берілген теңдеу үшін жалғыз. Бұл теореманы уақытында Коши беріп дәлелдеген. Сондықтан дифференциялдық теңдеудің дербес шешімін табуды Коши есебі дейді. Енді жоғарыда айтылған ұғымдардың геометриялық көзріністеріне көңіл ауд арайық. Дифференциялдық теңдеудің кез келегн дербес шешімінің графигі интегралдық қисық дейді. Осыдан жалпы шешімге сәйкес қисықтарды интегралдық қисықтар үйірі дейді. Сонда
\[{\theta}^{\prime}=\frac{\check{\sigma}}{\check{\sigma}}\]
дифференциялдық теңдеудің жалпы шешімі
\[\textstyle\theta=N{\tilde{\sigma}}\]
болса, осыған сәйкес инегралдық қзисықтар үйірі 1 - суретте.
2. Сурет 3. Сурет
\[{\hat{A}}_{1}\]
\[\theta^{\prime}=-{\frac{\delta}{\bar{\sigma}}}\]
жалпы шешілуі
\[\theta={\frac{\cal N}{\tilde{\vartheta}}}\]
үйірі 2 - суретте берілген.
\[\left.\partial\right|_{\sigma=\bar{\sigma}_{0}}=\partial_{0}\]
деген бастапқы шарт берілуі, ол интегралдық қисық өтетін
\[\textstyle P_{0}\left(\mathcal{X}_{0}\,\mathcal{Y}_{0}\right)\]
нүктесін берілуі мен пара - пар болады. Енді әртүрдегі дифференциялдық теңдеулерді қарастырайық.
1. 2. 2. Айнымалылалры ажыратылатын теңдеулер.
\[f_{1}(y)d y=f_{2}(x)d x\]
(1. 2. 2. 1. ) түрдегі дифференциялдық теңдеулерді айнымалылары ажыратылатын дифференциялдық теңдеулер дейді. Мұнда
\[f_{1}(y),f_{2}(x)\]
- берілген функциялар. Бұл теңдеулер әр айнымалылар теңдіктің өз дифференциялы болатын жағында ғана бар.
Сонда (1. 2. 2. 1) теңдіктің екі жағындада бір функциялардың дифференциялы болады. Яғни
\[\widetilde{{\cal O}}\]
және
\[\mathcal{E}\]
айнымалыларын дифференциялдарының орнындағы байланыс берілген.
\[\langle{\mathord{\mathord{I}}}\rangle=\langle{\mathcal{I}}\rangle\]
және
\[\langle{\mathord{\cal I}}\rangle\]
арасындағы
байланысты табу үшін екі жағында интегралдаймыз.
\[\S f_{1}(y)d y=\ \}f_{2}(x)d x+\breve{N}\]
(1. 2. 2. 2. )
Мысал1. 2. 2. 1.
\[{\mathcal O}^{\prime}\,\underline{{{-}}}\supset\mathcal O^{2}\,\mathcal O\!\mathcal O\]
дифференциялдық теңдеуі берілсін.
\[\mathcal{O}^{\prime}=\frac{d\mathcal{O}}{d\tilde{\sigma}}\]
. Осыдан
\[\frac{d\delta}{d\bar{\theta}}3\bar{\theta}^{2}\bar{\theta}\]
немесе
\[{\frac{d\bar{\theta}}{y}}3\bar{\theta}^{2}d x\]
болады. Бұл теңдеу
\[\partial\Big|_{\partial=\bar{\theta}_{0}}=2\]
бастапқы шартты қанағаттандырсын.
Шешуі.
\[{\frac{d\bar{\theta}}{y}}3\bar{\theta}^{2}d x\]
теңдеудің екі жағынан интеграл аламыз
\[{\mathfrak{Q}}_{\overline{{{y}}}}^{\overline{{{d}}}}={\mathfrak{H}}{\tilde{\sigma}}^{2}d x+{\tilde{N}}=\ln y=3{\frac{x^{3}}{3}}+\ln C\Rightarrow\]
\[\theta={\tilde{N}}{\dot{a}}^{\delta^{\delta^{\delta}}}\]
жалпы шешімі.
\[\mathcal{O}_{0}=\tilde{N}\check{\alpha}^{0}\ \mathrm{P}\ \ 2=\tilde{n}\]
Сонда дербес шешімі
\[\textstyle\theta=2\dot{\alpha}^{\dot{\sigma}^{\dot{\sigma}}}\]
болады.
Анықтама1. 2. 2. 2.
Теңдеудің екі жағында бір өрнекке көбейткенде айнымалылары теңдіктің екі жағына ажыратылатын болса, онда ол дифференциялдық теңдеулерді айнымалылары ажыратылатын теңдеулер дейді.
1. 2. 3. Біртекті және Сызықтық теңдеулер.
1. 2. 3. 1. Біртекті теңдеулер.
\[{\mathcal O}^{\prime}\,\longrightarrow\,{\mathcal{F}}(\chi,y)\]
теңдеуін біртекті дейді. Егер
\[f(x,y)\]
функциясын өз аргументінің қатынасының функциясы ретінде беруге болатын болса
\[f(x,y)=\phi_{\underline{{{\mathrm{c}}}}}^{\underline{{{\alpha}}}\underline{{{\hat{O}}}}}\underline{{{\hat{\Phi}}}}\]
(1. 2. 3. 1. 1. )
Мысал1. 2. 3. 1. 1
.
\[(x\mathcal{O}-\ \mathcal{O}^{2})d x-\ (x^{2}\ -\ 2x y)d y=0\]
\[\frac{d y}{d x}=\frac{x y-y^{2}}{x^{2}\cdot2x y}=\frac{\frac{y}{x}\cdot\frac{\exp{\frac{x}{\phi}}}{x}}{1-2\frac{y}{x}}\]
сонда
\[{\frac{y}{x}}=U\]
болса
\[{\mathcal G}\ =\tilde{\mathcal G}U\]
\[\mathcal{O}^{\prime}=\frac{U-\quad U^{2}}{1-2\mathcal{O}}\]
бірақ
\[\theta^{\prime}=(x u)^{\prime}=u+x u^{\prime}\Rightarrow\]
\[{\frac{d u}{d x}}={\frac{1}{x}}-\;{\frac{u^{2}}{1-2u}}\;{\frac{1-2u}{u^{2}}}d u={\frac{d x}{x}}\Rightarrow\]
\[{\frac{d u}{u^{2}}}-{\frac{2d u}{u}}={\frac{d x}{x}}\textrm{p}\,\,{\frac{1}{u}}-\,2\ln|u|=\ln|x|=\ln|e|\]
\[\frac{x^{2}}{y^{2}}e^{\frac{x}{u}}=l x=\frac{x}{y^{2}}e^{\frac{x}{u}}=e\]
1. 2. 3. 2. Сызықтық теңдеулер.
\[y^{\prime}+p(x)y=g(x)\]
(1. 2. 3. 2. 1. ) түрінде берілген теңдеудің сызықтық дифференциялды теңдеуі дейді. Бұл жерде белгісіз функция және оның туындысы сызықты қатынаста берілген.
\[p({\boldsymbol{x}})\]
және
\[g(x)\]
- белгілі функциялар
\[\textstyle{\mathcal{X}}\]
- қа тәуелді (1. 2. 3. 2. 1. ) теңдеуді
\[y=u\nu\]
деп алып оны айнымалылары ажыратылатын екі теңдеуге әкелуге болады. Сонда
\[y^{\prime}=(u\nu)^{\prime}=u^{\prime}\nu+u\nu^{\prime}\]
(1. 2. 3. 2. 2. ) (1. 2. 3. 2. 2. )
(а) қойсақ
\[u^{\prime}\nu+u\nu^{\prime}\,+\,p(x)u\nu=g(x)\]
болады
\[u^{\prime}\nu+u(\nu^{\prime}\ +\mathcal{P}(x)\nu)=g(x)\]
(1. 2. 3. 2. 3. )
Енді
\[{\boldsymbol{\nu}}\]
- ның бір дербес шешімін аламыз
\[\nu^{\prime}\ +\ p(x)\nu=0\]
(1. 2. 3. 2. 4. )
\[{\frac{d\nu}{d x}}=-\ p(x)\nu\Rightarrow\]
\[{\frac{d\nu}{d x}}=-\ P(x)d x\operatorname{P}\ \ln\nu=-\ \textstyle P(x)d x\]
осыдан
\[\nu=e^{-\ \int(x)d x}\]
(1. 2. 3. 2. 1) - деп
\[u^{\prime}v=g(x)\]
болады
\[{\cal M}^{'}\,e^{-}\,\,\mathrm{J}^{(x)d x=g(x)}\]
\[{\frac{d u}{d x}}e^{-\mathbf{\partial}^{p(x)}d x}=g(x)\Rightarrow\]
\[d u e^{-\mathbf{\hat{Q}}^{p(x)}}=g(x)d x\mathbf{\hat{m}}\]
\[d u=e^{-\bar{\Theta}^{(\ast)}}=g(x)d x\Rightarrow\]
\[u=\begin{array}{l l}{{\oint(x)e^{{\oint(x)}d x}}d x+C}\end{array}\]
сонда
Бұл (1. 2. 3. 2. 1. ) теңдеудің жалпы шешімі
Мысал1. 2. 3. 2. 1.
\[y^{'}\ -\ \ 2x y=1\]
мұнда
\[p(x)=-2x\]
,
\[g(x)=1\]
\[y=e^{-\bar{\Phi}^{\;2d x}\bar{\subseteq}\!e^{-\bar{\Phi}^{2d x}}d x+C\frac{\bar{\Phi}}{\hat{\Omega}}}=e^{x^{2}}\left[\frac{\vert x^{2}\,d x+C\vert}{\S}\right]\]
\[y_{0}=0\quad x_{0}=0\Rightarrow\]
\[y=e^{x^{2}}\;\;\stackrel{\textstyle\Gamma-x^{2}}{\textstyle d x}\]
(1. 2. 3. 2. 5. ) Теңдеуге анықталған интегралды пайдалансақ
\[y=e^{\Phi}{}^{\left(x\right)d x}\frac{\hat{\bf e}}{\hat{\bf e}}_{\hat{\otimes}}^{x}\vartheta\langle\,x\rangle^{\hat{\sigma}^{(x)d x}}+C^{\hat{\bf I}}\,\]
\[y\Bigl\vert_{x=x_{0}}=y_{0}\Rightarrow\]
\[\tilde{n}\,=\tilde{\sigma}_{0}\]
(1. 2. 3. 2. 6. )
1. 2. 4. Толық дифференциялдағы теңдеулер.
Анықтама1. 2. 4. 1.
\[P(x g)d x+Q(x y)d y=0\]
(1. 2. 4. 1. ) түріндегі өрнектің егер оң жағындағы өрнек бір
\[F(\,x y)\]
функциясының толық дифференциялы болса, онда ондай теңдеулерді толық дифференциялданатын теңдеулер дейді.
(1. 2. 4. 1. ) толық дифференциялдық теңдеу болса, онда
\[d F(x y)=\;0\Rightarrow\]
\[d F(x y)=P(x y)d x+Q(x y d y=0\Rightarrow\]
\[F(x y)=C\]
шынындада
\[y=\phi\left(x\right)\]
теңдеудің шешімі болса, онда
\[F\left[x\phi(x)\right]=\ C\Rightarrow\]
\[F(\,x\phi(x))=d C=0\]
осыдан
\[P(x y)d x+Q(x y)d y\]
толық дифференциял болу үшін мына шарт орындалуы қажет
\[{\frac{\mathrm{d}P}{\mathrm{d}y}}={\frac{\mathrm{d}Q}{\mathrm{d}x}}\]
(1. 2. 4. 2. )
... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар


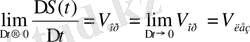 (1. 1. 2. 2. ) яғни
(1. 1. 2. 2. ) яғни
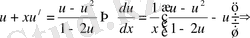
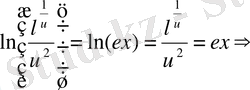
 (а) қойсақ
(а) қойсақ
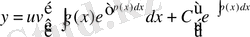 (1. 2. 3. 2. 5)
(1. 2. 3. 2. 5)


