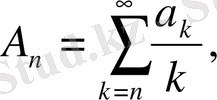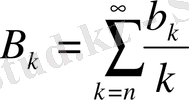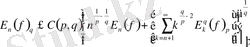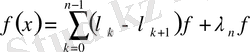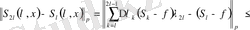Түрлендірілген Фурье қатары: ең жақсы жуықтаулар, коэффициенттердің интегралдық қасиеттері және Харди-Бельман түрлендірулері


МАЗМҰНЫ
Кіріспе . . .
Анықтамалар мен көмекші тұжырымдар . . .
I-тарау. Түрлендірілген Фурье қатары.
1. 1. Түрлендірілген Фурье қатарының ең жақсы жуықтауы туралы теорема . . .
1. 2. Түрлендірілген Фурье қатары үшін жалпы жағдай . . .
II-тарау. Коэффициенттері түрлендірілген Фурье қатары.
2. 1. Түрлендірілген Фурье коэффициентімен берілген функцияның интегралдық қасиеті . . .
Әдебиеттер.
Кіріспе.
Тригонометриялық қатарлар теориясы функциялар теориясының
бір саласы. Зерттеу нәтижесі метрикалық функциялар теориясының
әдісіне сүйенеді.
Метрикалық функциялар теориясының, оның ішінде, әсіресе, тригонометрикалық қатарлар теориясының Ресейде дамуына Н. Н. Лузиннің атақты « Интеграл және тригонометриялық қатарлар » (1915 ж) монографиясы үлкен әсерін тигізді. Бұл монография метрикалық функциялар теориясын зерттеушілердің негізгі кітабына, яғни кітап осы уақытқа дейінгі шешілген және шешілмеген көптеген проблемалардың көзіне айналды.
Тригонометриялық қатарлар теориясында негізгі назар мына сұрақтарға аударылады: жинақтылық, жинақсыздық, абсолютті жинақтылық, қатарлар коэффициенттері, түйіндес функциялар және оның біреу ғана болу проблемасы, жіктеу проблемасы, қосындылау.
1911 жылы Н. Н. Лузин мына түрдегі тригонометриялық қатарды құрды:

мұндағы
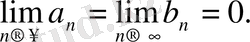
Бұл қатар
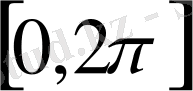 аралықтың барлық жерде дерлік жинақталмайды. Кейінгі маңызды қадам өз заманының заңғар математигі А. Н. Колмогоров тарапынан жасалды. Ол барлық жерде жинақталмайтын Фурье-Лебег тригонометриялық қатарын құрды.
аралықтың барлық жерде дерлік жинақталмайды. Кейінгі маңызды қадам өз заманының заңғар математигі А. Н. Колмогоров тарапынан жасалды. Ол барлық жерде жинақталмайтын Фурье-Лебег тригонометриялық қатарын құрды.
Диплом жұмысы 2 тараудан тұрады. Бірінші тарауда түрлендірілген Фурье қатардың ең жақсы жуықтаулары туралы терема және сол қатар үшін жалпы жағдай қарастырылады, ал екінші тарауда коэффициенттері Харди және Бельман түрлендірулері арқылы берілген Фурье қатары жайлы сөз болады. Сонымен қатар анықтамалар мен қажетті тұжырымдамалар да бар.
Анықтамалар мен қажетті тұжырымдар
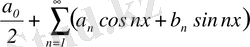
өрнек түріндегі қатарды тригонометриялық қатар дейміз, мұндағы
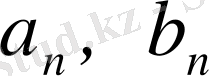 - тұрақты сандар (n=0, 1, 2, …, ) олар қатардың коэффициенттері деп аталады.
- тұрақты сандар (n=0, 1, 2, …, ) олар қатардың коэффициенттері деп аталады.
Егер
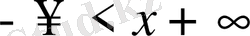 аралықта барлық х-тер үшін қатар жинақталса, онда қатар
аралықта барлық х-тер үшін қатар жинақталса, онда қатар
 периодты функция кескіндейді. Сондықтан, тригонометриялық қатарды кескіндейтін функция
периодты функция кескіндейді. Сондықтан, тригонометриялық қатарды кескіндейтін функция
 периодты функцияны қарастырады немесе берілген аралықтағы ұзындығы
периодты функцияны қарастырады немесе берілген аралықтағы ұзындығы
 -ге тең функцияны алады. Одан әрі оны периодты түрде жалғастырады, яғни
-ге тең функцияны алады. Одан әрі оны периодты түрде жалғастырады, яғни
 үшін
үшін
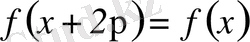 орындалады.
орындалады.
Тригонометриялық қатар тек математикада ғана емес, сонымен қатар оның көптеген салаларында үлкен роль атқарады. Ең алдымен оны айтпас бұрын, тригонометриялық және дәрежелік қатарлардың байланысын атап өтейік. Егер мына
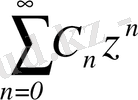 (2)
(2)
түрдегі қатарды қарастырсақ, мұндағы
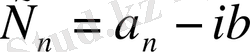 ,
,
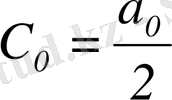 және
және
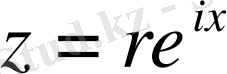 десек, онда (1) түрдегі қатар (2) түрдегі қатардың бірлік шеңберіндегі нақты бөлігі; (2) түрдегі қатардың жорамал бөлігі
десек, онда (1) түрдегі қатар (2) түрдегі қатардың бірлік шеңберіндегі нақты бөлігі; (2) түрдегі қатардың жорамал бөлігі
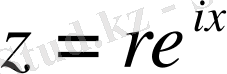 үшін қатар
үшін қатар
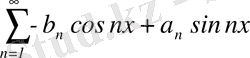 (3)
(3)
бар болады және (1) түрдегі қатарға түйіндес деп аталады.
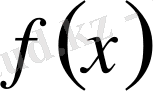 функциясы тригонометриялық қатардың қосындысы ғана емес, сонымен бірге
функциясы тригонометриялық қатардың қосындысы ғана емес, сонымен бірге
 аралығында бұл қатар бірқалыпты жинақталады дейік. Онда оның коэффициенттерін анықтау оңай болады.
аралығында бұл қатар бірқалыпты жинақталады дейік. Онда оның коэффициенттерін анықтау оңай болады.
Ол үшін мына теңдікті
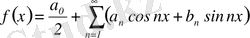
 немесе
немесе
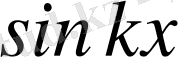 -қа көбейтіп, шектері
-қа көбейтіп, шектері
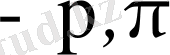 аралығында интегралдаймыз (бұл заңдылық) және былай десек,
аралығында интегралдаймыз (бұл заңдылық) және былай десек,
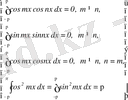 (4)
(4)
Нәтижесінде
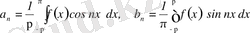 (5)
(5)
аламыз.
(4) түрдегі формулаларды Фурье формулалары деп атайды.
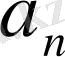 және
және
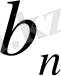 сандары - Фурье коэффициенттері, ақырында
сандары - Фурье коэффициенттері, ақырында
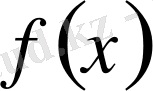 функциясынан шыққан коэффициенттері Фурье формуласымен анықталатын қатар
функциясынан шыққан коэффициенттері Фурье формуласымен анықталатын қатар
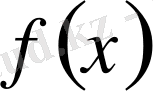 функциясы үшін Фурье қатары деген атқа ие. Біз оны
функциясы үшін Фурье қатары деген атқа ие. Біз оны
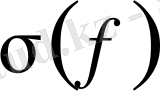 деп белгілейміз.
деп белгілейміз.
Тригонометриялық қатарлардың жинақтылығын үйренуде мына функциялар
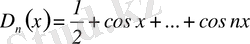 (6)
(6)
және
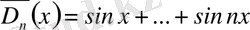 (7)
(7)
ерекше роль атқарады.
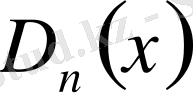 функциясын мына түрде жазуға болады:
функциясын мына түрде жазуға болады:
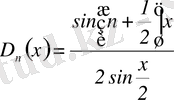 (8)
(8)
Шынында
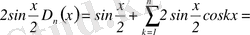
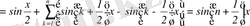 ,
,
Бұдан
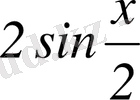 -ге бөлгеннен кейін (8) шығады.
-ге бөлгеннен кейін (8) шығады.
(8) өрнек Дирихле ядросы деп аталады, өйткені Дирихле оны алғашқы болып Фурье қатарының жинақтылығын үйренуде қолданған.
Сол сияқты
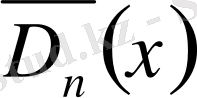 функциясы Дирихле ядросына түйіндес деп аталады, ол мына түрге ие
функциясы Дирихле ядросына түйіндес деп аталады, ол мына түрге ие
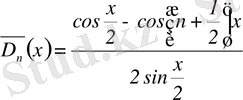 (9)
(9)
және тікелей тексеру оңай.
(8) және (9) формулаларынан бірден көрінеді, егер
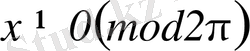 , онда
, онда
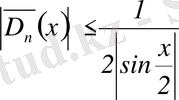
және
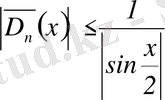 .
.
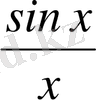 функциясының
функциясының
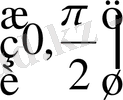 аралықта кемитін ескерейік (жай дифференциалдау арқылы көз жеткізуге болады), ал өйткені
аралықта кемитін ескерейік (жай дифференциалдау арқылы көз жеткізуге болады), ал өйткені
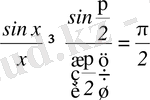 .
.
Демек,
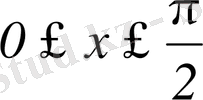 үшін
үшін
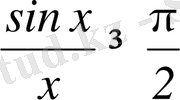 .
.
- және (6) қолданып,
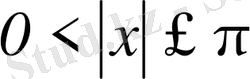 үшін
үшін
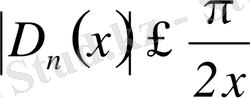
және
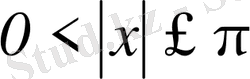 үшін
үшін
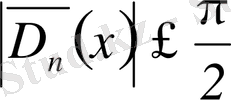
аламыз.
Бұл формулаларды алдағы уақытта жиі қолданамыз. Көбінесе
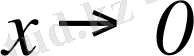 үшін
үшін
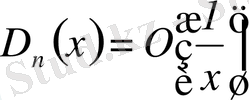 және
және
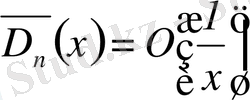
бағалаулары жеткілікті болады, кейде
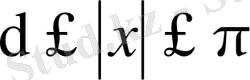 маңызды болады, онда
маңызды болады, онда
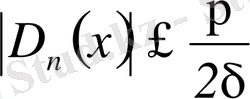 және
және
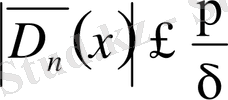 (10)
(10)
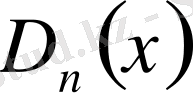 және
және
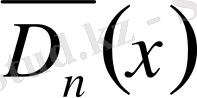 периодтылығы бойынша мынаны айтуға болады,
периодтылығы бойынша мынаны айтуға болады,
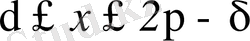 болса, (10) орындалады.
болса, (10) орындалады.
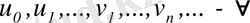 нақты сандар болсын,
нақты сандар болсын,
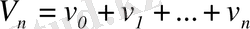 деп ұйғарайық.
деп ұйғарайық.
Онда
 және n үшін
және n үшін
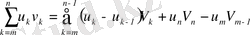 (11)
(11)
аламыз (егер m=0 болса, онда
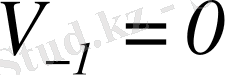 екеніне келісеміз) .
екеніне келісеміз) .
Бұл формула Абель түрлендіруі деп аталады, оңай дәлелденеді.
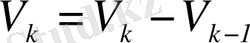 екенін ескеріп, осы өрнекті сол жақ бөлігіне қойып, мүшелерді топтауға болады.
екенін ескеріп, осы өрнекті сол жақ бөлігіне қойып, мүшелерді топтауға болады.
m=0 үшін дербес жағдайда
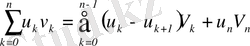 (12)
(12)
аламыз.
(11) және (12) формулалар бөліктеп интегралдауға ұқсас,
 интегралын
интегралын
 -ға келтіріп есептеу ыңғайлы және мұнда
-ға келтіріп есептеу ыңғайлы және мұнда
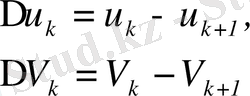
деп алып, (11) -ді мына түрде жазуға болады
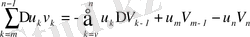 ,
,
яғни қарастырып отырған қосындыларымызды басқа қосындыларға келтіріп есептеуге көбінесе тиімді.
Дербес жағдайда қарастырып отырған тізбектеріміздің бірі монотонды кемитіндіктен бұл тиімді (барлық
 үшін
үшін
 болғандықтан,
болғандықтан,
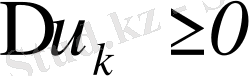 шығады) .
шығады) .
Абель түрлендіруінен бірден салдар аламыз:
Салдар.
Егер
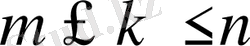 үшін барлық
үшін барлық
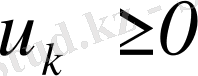 және
және
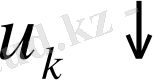 ,
,
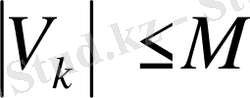 болса, онда
болса, онда
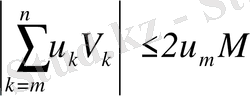 .
.
Шынында,
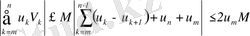 .
.
 санының орнына кейбір
санының орнына кейбір
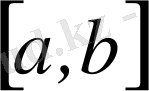 аралығында анықталатын
аралығында анықталатын
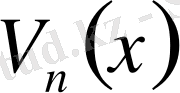 функциясын алған жағдайды қарастырайық.
функциясын алған жағдайды қарастырайық.
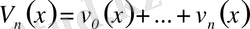
деп алсақ, мына лемманы аламыз:
Абель леммасы:
Егер
 0 және
0 және
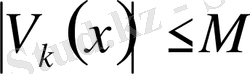 ,
,
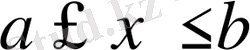 болса, онда қатар
болса, онда қатар
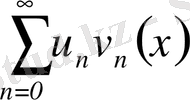
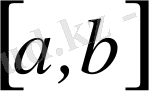 аралығында бірқалыпты жинақталады және оның
аралығында бірқалыпты жинақталады және оның
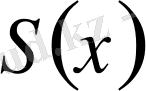 қосындысы үшін мына теңсіздік орындалады:
қосындысы үшін мына теңсіздік орындалады:
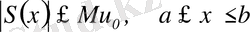 (13)
(13)
Дәлелдеу: Шынында,
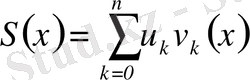
деп ұйғарайық. Онда (12) формула бойынша
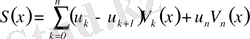 , (14)
, (14)
бұдан
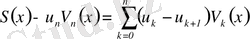 .
.
Өйткені
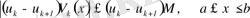 , (15)
, (15)
ал қатар
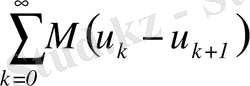
Теріс емес мүшелерімен жинақталады (
 0 бойынша) және
0 бойынша) және
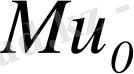 қосындысына ие, онда қатар
қосындысына ие, онда қатар
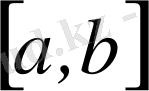 аралығында абсолютті және бірқалыпты жинақталады. Онда
аралығында абсолютті және бірқалыпты жинақталады. Онда
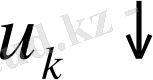 0 және (13) формуладан
0 және (13) формуладан
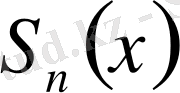
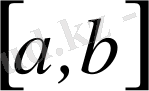 аралығында
аралығында
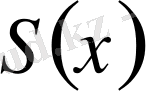 функциясына бірқалыпты жинақталады. Бұл (13) дұрыс және лемма дәлелденді.
функциясына бірқалыпты жинақталады. Бұл (13) дұрыс және лемма дәлелденді.
 функциясының
функциясының
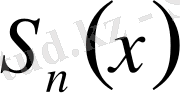 Фурье қатарының дербес қосындысы мына формуламен өрнектеледі:
Фурье қатарының дербес қосындысы мына формуламен өрнектеледі:
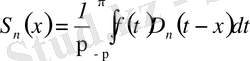 ,
,
мұндағы
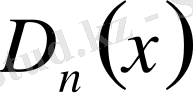 - Дирихле ядросы. Сондықтан чезардың қосындысы
- Дирихле ядросы. Сондықтан чезардың қосындысы
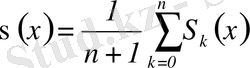
мына түрде жазылады:
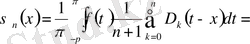
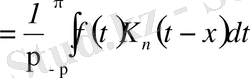 ,
,
мұндағы,
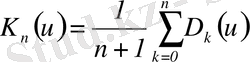 (16)
(16)
Сондықтан
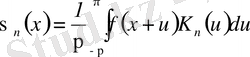 .
.
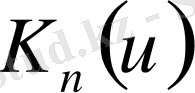 функциясы Фейер ядросы деп аталады. Оны ыңғайлы түрге келтірейік:
функциясы Фейер ядросы деп аталады. Оны ыңғайлы түрге келтірейік:
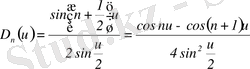
болғандықтан, онда
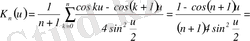
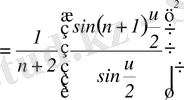 .
.
Сонымен,
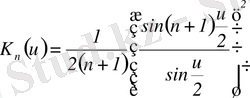 .
.
Осы өрнектен ядроның қасиетін қорытындылаймыз.
1)
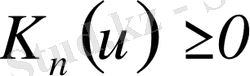 .
.
Бұл қасиет болашақта елеулі роль атқарады.
2)
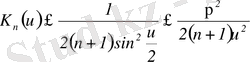 ,
,
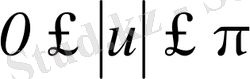 үшін аламыз, өйткені
үшін аламыз, өйткені
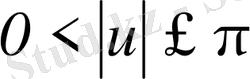 үшін,
үшін,
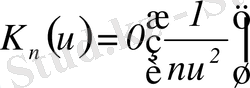
және
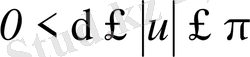 үшін,
үшін,
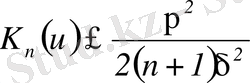 ,
,
бұдан
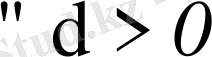 ,
,
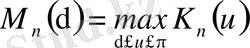
десек, мынаны аламыз:
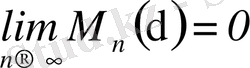 .
.
3)
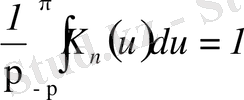 .
.
Бұл (16) формуладан және
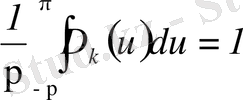 шығады
шығады
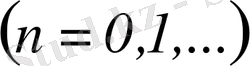 .
.
4) Егер
 , онда
, онда
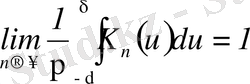 .
.
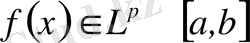 болсын, мұнда
болсын, мұнда
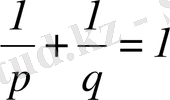 .
.
Мына теңсіздіктің дұрыстығын дәлелдейік:
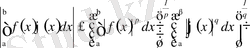
немесе қысқаша
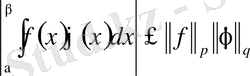 .
.
Бұл теңсіздік Гельдер теңсіздігі деп аталады.
Шынында,

десек,
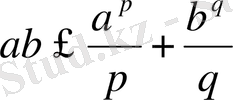
аламыз, мұнда
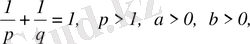
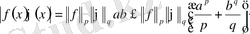 (17)
(17)
Бірақ
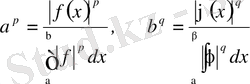 .
.
х бойынша интегралдап, мынаны табамыз:
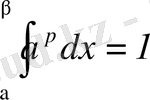 және
және
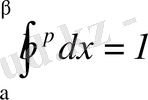
және (17) формуладан
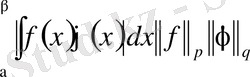
шығады. Бұл теңсіздікті дәлелдейді.
Ескерту.
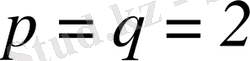 десек, Коши-Буняковский теңсіздігін аламыз:
десек, Коши-Буняковский теңсіздігін аламыз:
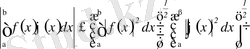
немесе
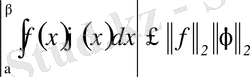 .
.
Егер
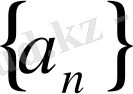 және
және
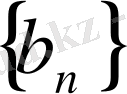 - 2 сандық тізбектері және
- 2 сандық тізбектері және
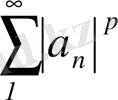 және
және
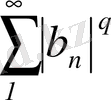
қатарлары жинақталса, онда
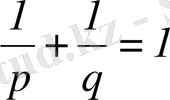
үшін
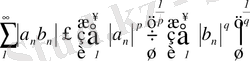
аламыз.
Ескерту.
Гельдер теңсіздігі
 және
және
 -те сақталады, егер
-те сақталады, егер
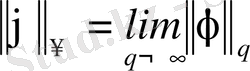 (18)
(18)
дегенге келіссек.
(18) оң бөлігінің шегі бар екенін көрсетейік, егер функция маңызды шектелген және ол аңызды жоғарғы шекарасына тең болса. Сонда
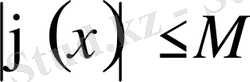 (19)
(19)
болатындай
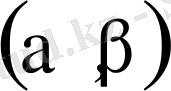 аралығында маңызды жоғарғы шекарадан М саны табылады және басқа жағынан
аралығында маңызды жоғарғы шекарадан М саны табылады және басқа жағынан
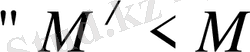 үшін
үшін
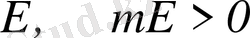 көбейтіндісі табылады, мұнда
көбейтіндісі табылады, мұнда
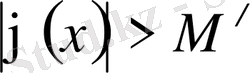 .
.
Шынында, егер (20) барлық жерде дерлік орындалса, онда
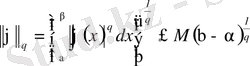 ,
,
сондықтан
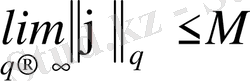 .
.
Екінші жағынан, егер
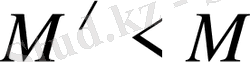 және Е бойынша
және Е бойынша
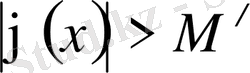 6 онда
6 онда
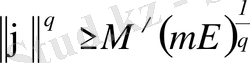 ,
,
өйткені
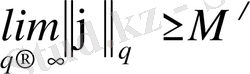 ,
,
ал
 сан болғандықтан,
сан болғандықтан,
 , онда
, онда
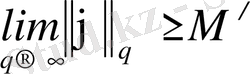 ,
,
осыдан
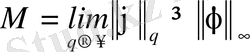
шығады.
Гельдер теңсіздігінен алда керек болатынын бір салдарды келтірейік:
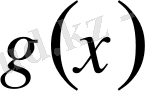 - шектелген,
- шектелген,
 периодты, теріс емес және
периодты, теріс емес және
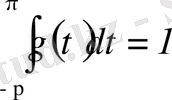
функциясы болсын.
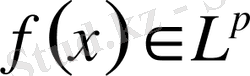 дейік.
дейік.
Егер
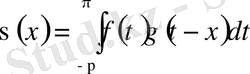
деп белгілесек, онда
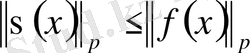 .
.
Шынында, Гельдер бойынша
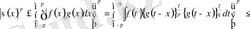
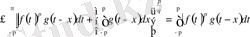 ,
,
бұдан шығатыны:
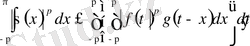
және интегралдың ретін өзгертіп,
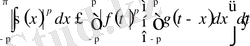 .
.
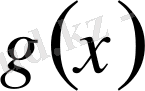 -тің периодтылығы бойынша
-тің периодтылығы бойынша
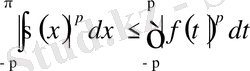 аламыз және
аламыз және
 дәрежеге шығарып, ізделінді теңсіздікті аламыз.
дәрежеге шығарып, ізделінді теңсіздікті аламыз.
Теорема:
Егер
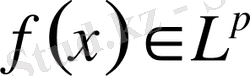
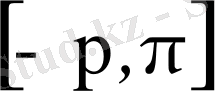 және
және
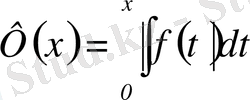 болса,
болса,
онда
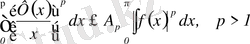 , (20)
, (20)
мұндағы
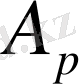
 -дан тәуелді.
-дан тәуелді.
Дәлелдеу.
Бұл теңсіздік Харди теңсіздігі деп аталады. Бұған көз жеткізу үшін ең алдымен біз, егер
 болғанда бөліктеп интегралдауды алатынымызды ескеруіміз керек:
болғанда бөліктеп интегралдауды алатынымызды ескеруіміз керек:
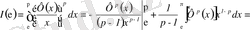
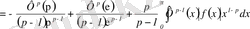 ,
,
яғни,
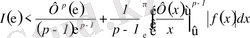 .
.
Гельдер теңсіздігінен
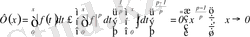 ,
,
содан
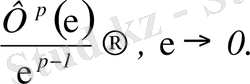
Гельдер теңсіздігінің тағы да қолдана отырып
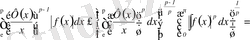
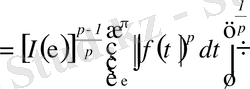 .
.
Бұдан мынаны аламыз:
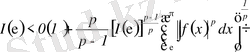 .
.
Одан соң теңсіздіктің екі жағын да
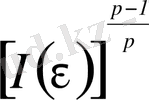 -ге бөлеміз, онда
-ге бөлеміз, онда
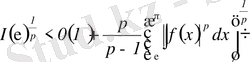
аламыз. Егер
 шекке көшсек, ол мынаны береді:
шекке көшсек, ол мынаны береді:
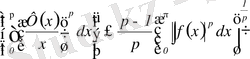 ,
,
яғни соңғы теңсіздікті сол жағындағы интегралдың бар болатынын дәлелдедік және ол үшін мына бағалауды береді:
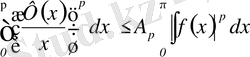
мұндағы
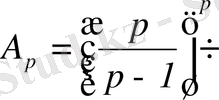 - тұрақты, тек
- тұрақты, тек
 -дан тәуелді.
-дан тәуелді.
Хаусдорф-Юнга теоремасы:
1) Айталық
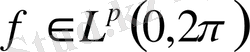 және
және
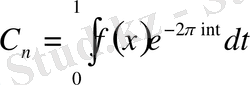
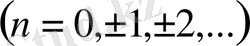 (21)
(21)
яғни
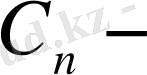 Фурье коэффициенттері
Фурье коэффициенттері
 де ортогональды және нормалданған жүйе болсын және
де ортогональды және нормалданған жүйе болсын және
 жүйесі
жүйесі

Онда
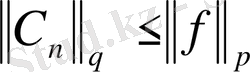 (22)
(22)
2) Егер
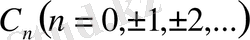 сан тізбегі
сан тізбегі
 болса және
болса және
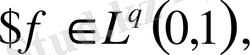 ол (21) шарттарын қанағаттандырса және
ол (21) шарттарын қанағаттандырса және
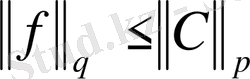
Харди-Литтльвуд теоремасы:
1)
 функциясының Фурье қатары мына түрде болсын
функциясының Фурье қатары мына түрде болсын
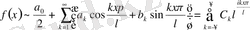
және
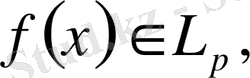
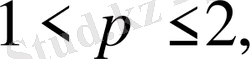 онда
онда
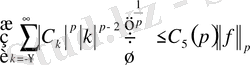
2) Айталық
 -комплекс сандар
-комплекс сандар
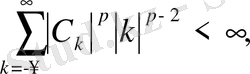
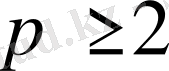
болсын, онда
 қандайда бір
қандайда бір
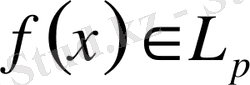 функциясының Фурье коэффициенті болады, және
функциясының Фурье коэффициенті болады, және
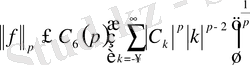
Айталық
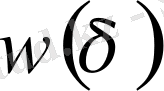 -кемімейтін,
-кемімейтін,
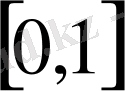 кесіндісінде үзіліссіз функция және мына шарттарды қанағаттандыратын болсын
кесіндісінде үзіліссіз функция және мына шарттарды қанағаттандыратын болсын
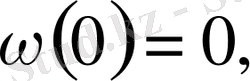
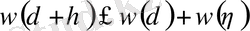
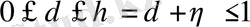
мұндай функциялар үзіліссіздік модулі деп аталады. Барлық
 -периодты өлшемді функциясын
-периодты өлшемді функциясын
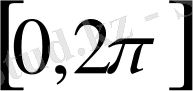 интервалында
интервалында
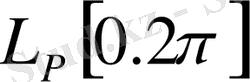 арқылы белгілейміз.
арқылы белгілейміз.
Егер
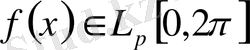 ,
,
 болса
болса
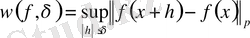
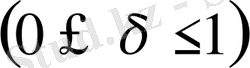
 функциясының үзіліссіздік модулі деп аталады.
функциясының үзіліссіздік модулі деп аталады.
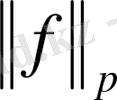 -белгісі
-белгісі
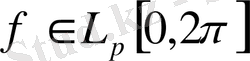
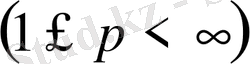 функциясының нормасын білдіреді
функциясының нормасын білдіреді
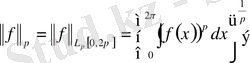
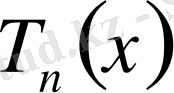 -дәрежесі
-дәрежесі
 -нен аспайтын полином болсын.
-нен аспайтын полином болсын.
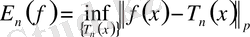 ,
,
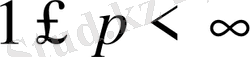
шамасы реті
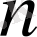 -нен аспайтын тригонометриялық полином тізбегімен
-нен аспайтын тригонометриялық полином тізбегімен
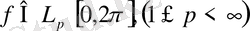 функцияның ең жақсы жуықтауы деп аталады.
функцияның ең жақсы жуықтауы деп аталады.
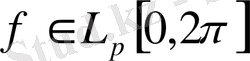 функцияның фурье коэффициенты тригонометриялық жүйе бойынша мына тендіктермен өрнектеледі:
функцияның фурье коэффициенты тригонометриялық жүйе бойынша мына тендіктермен өрнектеледі:
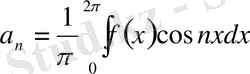
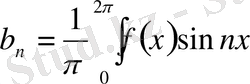
онда
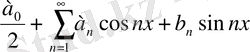
қатары
 функцияның Фурье қатары деп аталады.
функцияның Фурье қатары деп аталады.
Айталық
 -нольге ұмтылатын монотонды кемімелі
-нольге ұмтылатын монотонды кемімелі
оң сандар тізбегі болсын.
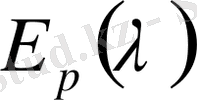 -арқылы әрбір
-арқылы әрбір
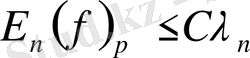
үшін
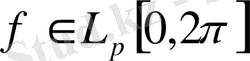 функциялар класын белгілейміз мұндағы
функциялар класын белгілейміз мұндағы

 -дан тәуелді оң тұрақтылар.
-дан тәуелді оң тұрақтылар.
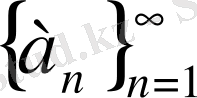 тізбегі квазимонотонды деп аталады, егер
тізбегі квазимонотонды деп аталады, егер
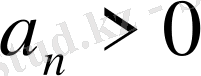 ,
,
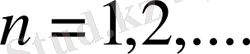 және
және
 табылып,
табылып,
 болғанда мына
болғанда мына
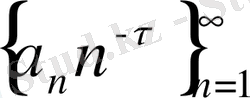 тізбек кемімелі монотонды нольге ұмтылса.
тізбек кемімелі монотонды нольге ұмтылса.
Егер
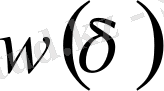 үзіліссіздік модулі және
үзіліссіздік модулі және
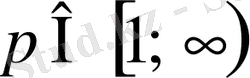 саны,
саны,
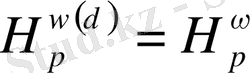
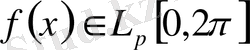 функцияның барлық нүктедегі жиынын білдіреді және олардың әрбірі үшін
функцияның барлық нүктедегі жиынын білдіреді және олардың әрбірі үшін
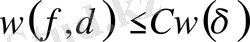

орындалады.
Айталық,
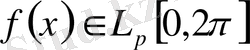 ,
,
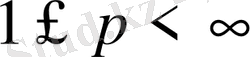 оның Фурье қатары:
оның Фурье қатары:
(23)
Екінші тарауда мынадай Харди және Бельман түрлендірулерін қарастырамыз:
Т:
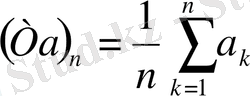
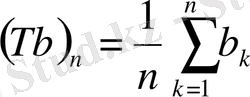
және
Т*:
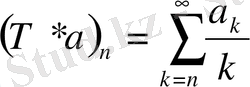
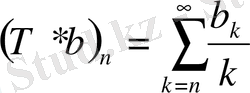
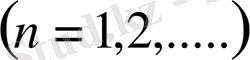
Теорема А. (Г. Харди)
Айталық
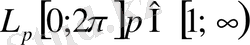 класында жататын
класында жататын
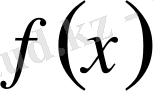
функцияның Фурье коэффициенттері
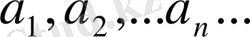 , , ал мына
, , ал мына
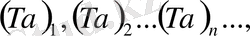
тізбек қандайда бір түрлендірілген Фурье коэффициенттері болсын.
Кейбір жағдайларда түрлендірілген
 Фурье қатары үшін
Фурье қатары үшін
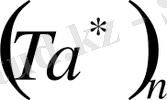 өрнегі
өрнегі
алмаймыз, бірақта егер
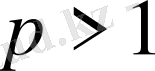 болса
болса
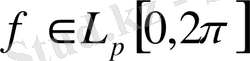 және
және
 Фурье қатарын аламыз, Бельман дәлелдегендей қатарымыз
Фурье қатарын аламыз, Бельман дәлелдегендей қатарымыз
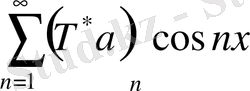 қандайда бір
қандайда бір
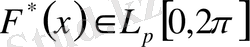 функциясының Фурье қатары болады.
функциясының Фурье қатары болады.
Теорема В. (Бельман)
Айталық
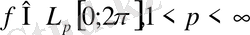 және
және
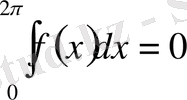 болсын, онда қатар
болсын, онда қатар
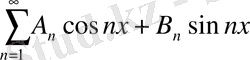
қандайда бір
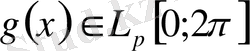 функцияның Фурье қатары болады, мұндағы
функцияның Фурье қатары болады, мұндағы
Теорема С. (П. Л. Ульянов)
Айталық
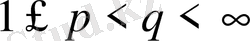 болсын. Егер
болсын. Егер
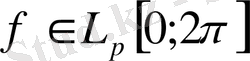 және
және
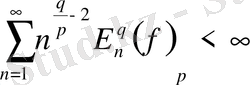 болса, онда
болса, онда
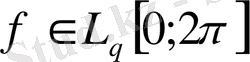 жәнеде мынадай бағалауды аламыз.
жәнеде мынадай бағалауды аламыз.
Лемма 1 (М. Тиман)
Айталық
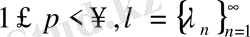 кемімелі он сандар тізбегі болсын және ол
кемімелі он сандар тізбегі болсын және ол
 , нольге ұмтылсын. Онда мына функция
, нольге ұмтылсын. Онда мына функция
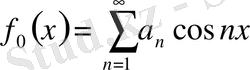
 (24)
(24)
мұндағы
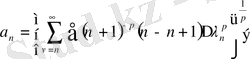
 класында жатады.
класында жатады.
Дәлелдеу. Алдымен (24) -қатардың коэффициенттерінің кемімелі
және мына шартты көрсетейік:
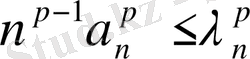
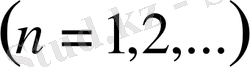 (25)
(25)
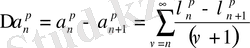
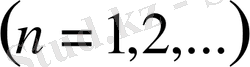 (26)
(26)
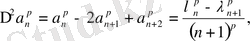
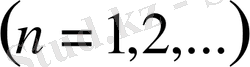 (27)
(27)
Енді айырманы қарастырайық:
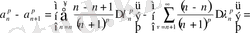
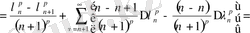
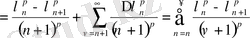
Сонымен (26) теңдігі дәлелденді.
Тізбек
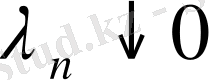 және
және
 онда
онда
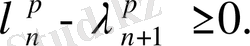
(26) теңдігінен:
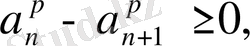
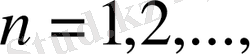 яғни (24) қатарының коэффициенттері кемімелі, бұдан (25) тенсіздігінің дұрыстығын көрсетейік.
яғни (24) қатарының коэффициенттері кемімелі, бұдан (25) тенсіздігінің дұрыстығын көрсетейік.
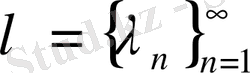 монотонды кемімелі тізбек болғандықтан, шығатыны:
монотонды кемімелі тізбек болғандықтан, шығатыны:
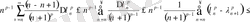
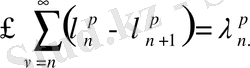
(27) теңдігінің дұрыстығын көрсетейік:
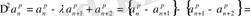
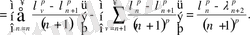
(27) өрнегі дәлелденді.
Келесі қатарды қарастырамыз:
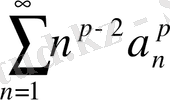
 (28)
(28)
Абель түрлендіруінің көмегімен:
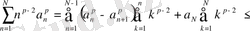
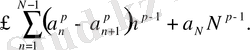
Қос қосындының ретін ауыстырып,
 ұмтылдырғаннан соң (25), (26) және
ұмтылдырғаннан соң (25), (26) және
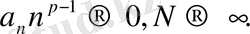
екенін ескере отырып:
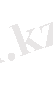
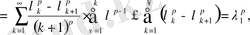
яғни (28) - қатар жинақталады.
Харди-Литтьлвуд теоремасын қолдансақ, онда
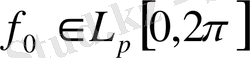
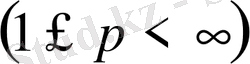
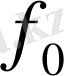 функциясының Фурье коэффициенті монотонды нольге ұмтылатын болғандықтан, Конюшков теоремасы бойынша барлық
функциясының Фурье коэффициенті монотонды нольге ұмтылатын болғандықтан, Конюшков теоремасы бойынша барлық
 үшін
үшін
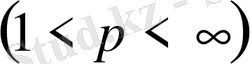 мына теңсіздік орындалады:
мына теңсіздік орындалады:
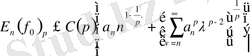 (29)
(29)
Келесі қатарға Абель түрлендіріуін қолдансақ.
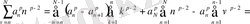
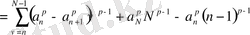
теңдігі шығады.
Тізбек
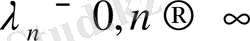 және
және
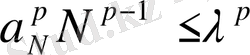 , онда
, онда
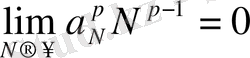 .
.
(25) және (26) теңсіздіктерін пайдаланып:
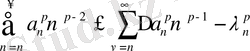 (30)
(30)

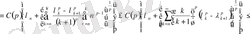
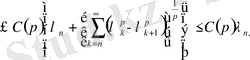
яғни
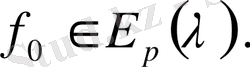
Сонымен
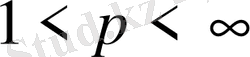 үшін дәлелденді.
үшін дәлелденді.
Енді
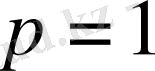 үшін дәлелдейік. (28) қатары монотонды, жинақталады және ол квазимонотонды.
үшін дәлелдейік. (28) қатары монотонды, жинақталады және ол квазимонотонды.
Абель түрлендіруін және Дирихле мен Фейердің ядросын пайдаланып:
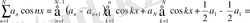
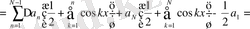
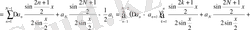
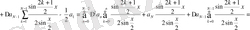
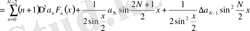
мұндағы
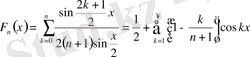
Фейердің n-ші ретті ядросы.
 және
және
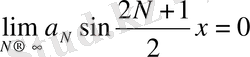
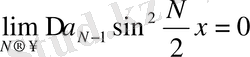
 Бұдан
Бұдан
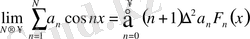
яғни
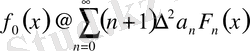
және
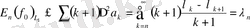
лемма далелденді.
Ескерту. Квазимонотонды шарттары жай монотонды шарттарына қарағанда кеңдеу ұғым.
Айталық тізбек
 ,
,
 және квазимонотонды болсын.
және квазимонотонды болсын.
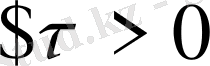 және
және
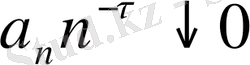
 ал керісінше дұрыс емес.
ал керісінше дұрыс емес.
Айталық
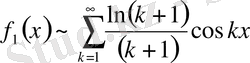
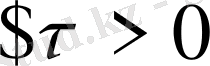 :
:
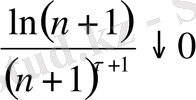 яғни
яғни
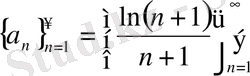
тізбегі квазимонотонды, бірақ
 тізбек монотонды емес, яғни
тізбек монотонды емес, яғни
Лемма2 (С. Б. Стечкин) .
Егер
 үзіліссіздік модулі және сондай
үзіліссіздік модулі және сондай
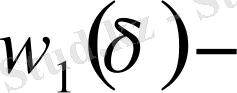 дөңес жоғары функциясы табылса, онда
дөңес жоғары функциясы табылса, онда
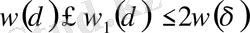

I-тарау. Түрлендірілген Фурье қатары.
§1. Түрлендірілген қатардың ең жақсы жуықтауы туралы теорема.
Айталық
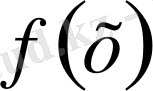
 периодты функциясы
периодты функциясы
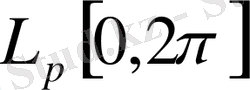 ,
,
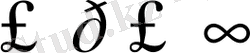
Фурье қатарына жіктелсін:
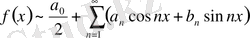 (1)
(1)
Мұндағы
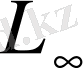
 -аралығында маңызды шектелген функциялардың сыныбы.
-аралығында маңызды шектелген функциялардың сыныбы.
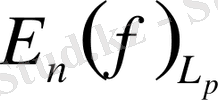
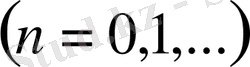 - деп
- деп
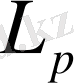 метрикасындағы
метрикасындағы
 ретті
ретті
 тригонометрикалық полиномдардың ең жақсы жуықтауларын, ал
тригонометрикалық полиномдардың ең жақсы жуықтауларын, ал
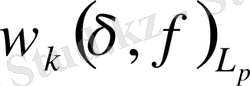 -арқылы
-арқылы
 метрикасындағы
метрикасындағы
 функциясының
функциясының
 -ретті үзіліссіздік модулін белгілейік.
-ретті үзіліссіздік модулін белгілейік.
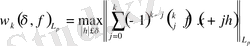
Теорема 1.
Айталық
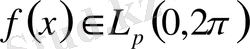 функциясының
функциясының
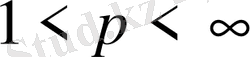 Фурье қатары:
Фурье қатары:
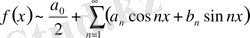 (1)
(1)
үшін
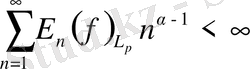 (2)
(2)
мұндағы
 - қандайда бір нақты сан, шарты орындалса, онда
- қандайда бір нақты сан, шарты орындалса, онда
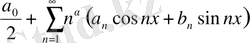 (3)
(3)
қатары кеңістігінде жатқан қандайда бір -функцияның Фурье қатары болады жәнеде
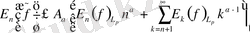
 (4)
(4)
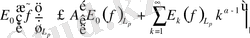
оның ең жақсы жуықтауы үшін теңсіздіктері орындалады, мұндағы
 -тұрақтысы
-тұрақтысы
 және
және
 -дерден тәуелсіз.
-дерден тәуелсіз.
Дәлелдеу.
 және
және
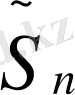 -деп (1) және (3) өрнектерінің сәйкес дербес қосындысын белгілейік және
-деп (1) және (3) өрнектерінің сәйкес дербес қосындысын белгілейік және
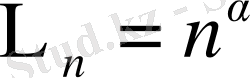
болсын. Абель түрлендіруінің көмегімен:
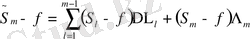
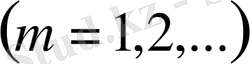
мұндағы
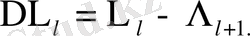
Демек
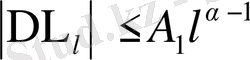
Онда
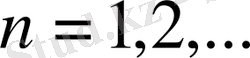 болғанда кез-келген
болғанда кез-келген
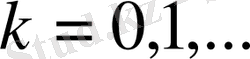 үшін:
үшін:
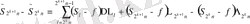
орындалады.
М. Рисс теоремасы
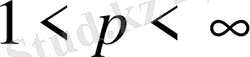 болғанда
болғанда
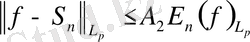 теңсіздігі шығады, мұндағы
теңсіздігі шығады, мұндағы
 -тұрақты. Осы теңсіздікті пайдаланамыз.
-тұрақты. Осы теңсіздікті пайдаланамыз.

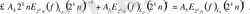
Одан ары қарай
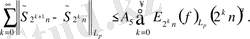
келесі теңсіздіктен
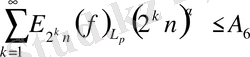
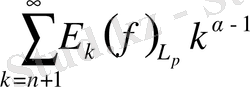 (5)
(5)
екенін ескере отырып,
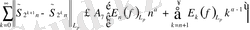 (6)
(6)
бағалауы шығады.
Бұдан (2) шарты бойынша:
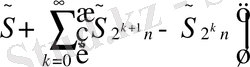
қатары
 -метрикасында қандайда бір
-метрикасында қандайда бір
 функциясына жинақталады. Бұл функцияның Фурье қатары (3) болады.
функциясына жинақталады. Бұл функцияның Фурье қатары (3) болады.
Сонымен,
 болғанда
болғанда
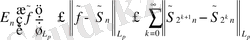
және (6) теңсіздігі
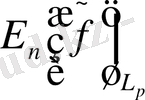 үшін керекті бағалауды береді.
үшін керекті бағалауды береді.
Сонымен
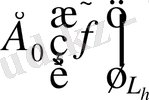 -ды бағалау ғана қалды.
-ды бағалау ғана қалды.
Үшбұрыш теңсіздігі бойынша:
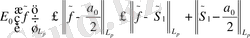
 болғанда
болғанда
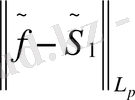 үшін (4) - бағалау орындалады.
үшін (4) - бағалау орындалады.
Ары қарай
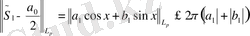
Айталық
 дегеніміз мына
дегеніміз мына
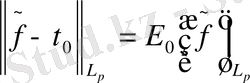 теңдік орындалатын сан болсын.
теңдік орындалатын сан болсын.
Онда
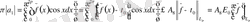
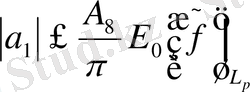
 үшін бағалау осыған ұқсас. Сонымен біз
үшін бағалау осыған ұқсас. Сонымен біз
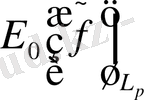 үшін қажет бағалауды алдық. Теорема дәлелденді.
үшін қажет бағалауды алдық. Теорема дәлелденді.
Салдар.
1-теорема шарттарын орындағанда әрбір натурал
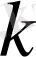 үшін
үшін
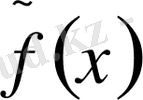 - функциясының
- функциясының
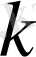 -ретті үзіліссіздік модулі
-ретті үзіліссіздік модулі
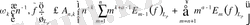
 (7)
(7)
бағаланады.
Ең жақсы жуықтаудың бізге қажетті кейбір қасиеттерін келтірейік:
1) .
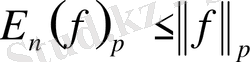
2) .
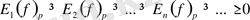
3) .
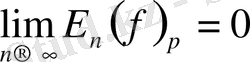
4) .
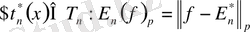
5) . Егер
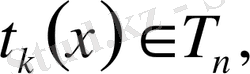
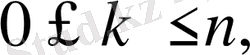 онда
онда
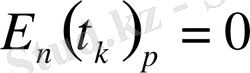
6) .
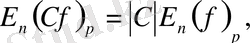

7) .
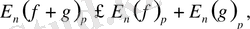

8) . Егер
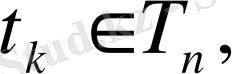
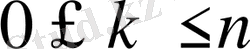 онда
онда
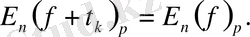
§2. Түрлендірілген Фурье қатары үшін жалпы жағдай.
Теорема 1.
Айталық
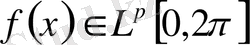
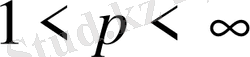 және
және
 нақты саны
нақты саны
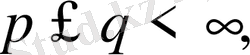 ал
ал
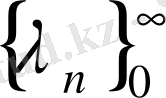 -өспелі монотонды нақты сандар тізбегі болсын. Егер
-өспелі монотонды нақты сандар тізбегі болсын. Егер
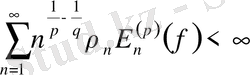 (1)
(1)
мұндағы
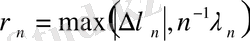 онда қатар
онда қатар
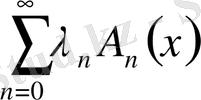 (2)
(2)
 -функциясының
-функциясының
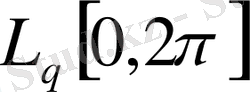 класында жатады және мына теңсіздік орындалады
класында жатады және мына теңсіздік орындалады
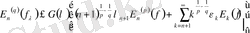 (3)
(3)
мұндағы
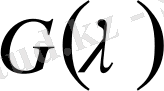 -тұрақтысы
-тұрақтысы
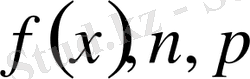 және
және
 -лардан тәуелсіз.
-лардан тәуелсіз.
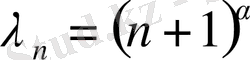
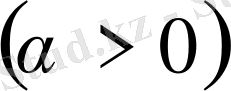 және
және
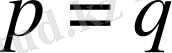 болса жоғарыдағы Конюшков теоремасы келіп шығады. Теңсіздіктің дәлелдеу жолы Коньюшковтың дәлелдеу жолына ұқсас.
болса жоғарыдағы Конюшков теоремасы келіп шығады. Теңсіздіктің дәлелдеу жолы Коньюшковтың дәлелдеу жолына ұқсас.
Леммалар. Бізге келесі леммалар қажет:
Лемма 1.
Егер
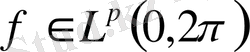
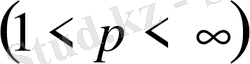 болса, онда
болса, онда
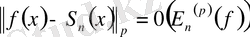
Лемма 2.
Егер
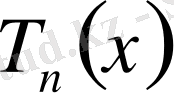 -
-
 ші ретті тригонометриялық полином және
ші ретті тригонометриялық полином және
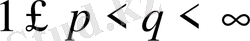 болса, онда
болса, онда
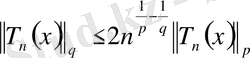
Лемма 3.
Егер
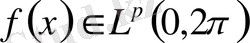 болса, онда
болса, онда
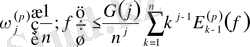
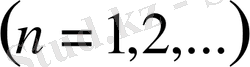
Лемма 4.
Айталық
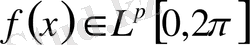
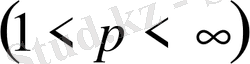 және
және
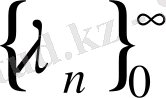 -нақты сандар тізбегі болсын. Егер
-нақты сандар тізбегі болсын. Егер
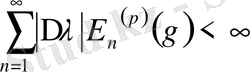
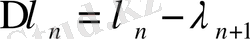
болса, онда
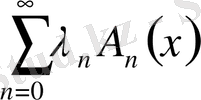 түрлендірілген Фурье қатары
түрлендірілген Фурье қатары
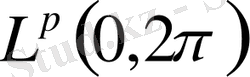 класында жатады.
класында жатады.
Дәлелдеу 1-теорема.
(1) шарттан және лемма 4 бойынша (2) түрлендірілген қатар қандайда бір
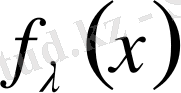 функциясында жинақталады және ол
функциясында жинақталады және ол
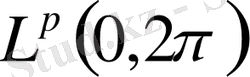 класында жатады.
класында жатады.
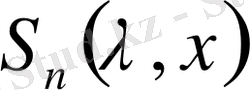 - (2) қатардың дербес қосындысы болсын.
- (2) қатардың дербес қосындысы болсын.
Абел түрлендіруін пайдалансақ (2) түрлендіруден
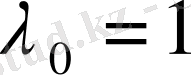 деп алуға болатындықтан
деп алуға болатындықтан
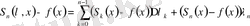
және де
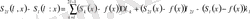
1-лемманы қолдансақ, шығатыны:
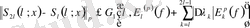
және 2-лемманы қолданғанда
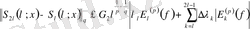 (4)
(4)
мұндағы
 және
және
 -нольден ерекше абсолютті тұрақты.
-нольден ерекше абсолютті тұрақты.
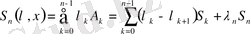
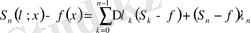
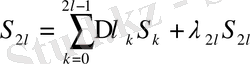
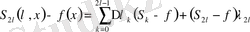
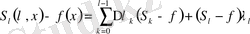
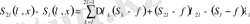
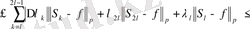
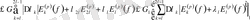
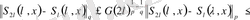
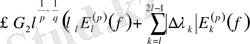
Егер
 тізбегі монотонды өспелі және дөңес болса, онда
тізбегі монотонды өспелі және дөңес болса, онда
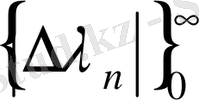 тізбегі барлық
тізбегі барлық
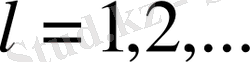 үшін монотонды кемімейтін болады, бұдан
үшін монотонды кемімейтін болады, бұдан
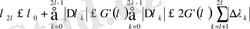
Егер
 тізбегі монотонды өспелі және ойыс болса, онда
тізбегі монотонды өспелі және ойыс болса, онда
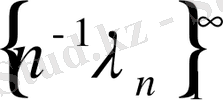 тізбегі кез-келген
тізбегі кез-келген
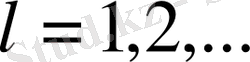 үшін монотонды өспейтін тізбек болады, яғни
үшін монотонды өспейтін тізбек болады, яғни
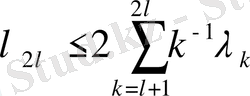
Сонымен мына теңсіздік орындалады:
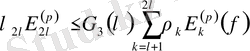
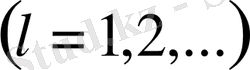 (5)
(5)
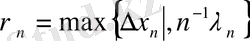
(4) және (5) теңсіздіктерден біз кез-келген
 үшін төмендегі өрнекті аламыз
үшін төмендегі өрнекті аламыз
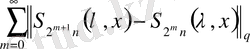 (6)
(6)
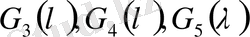 және
және
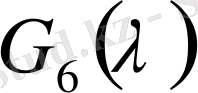
 -дан тәуелді тұрақтылар.
-дан тәуелді тұрақтылар.
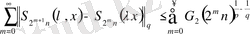
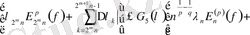
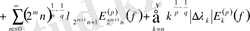


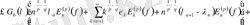
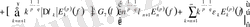
Келесі бағалаулардан:
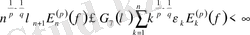
 үшін (6) -қатардың жинақталатыны шығады.
үшін (6) -қатардың жинақталатыны шығады.
Демек
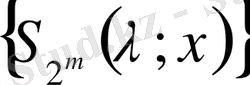 тізбегі
тізбегі
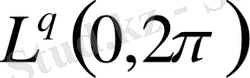 -метрикасында жатқан қандайда бір
-метрикасында жатқан қандайда бір
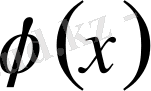 - функциясына жинақталады, яғни
- функциясына жинақталады, яғни
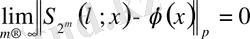
Гольдер теңсіздігі бойынша
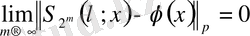
Лемма 1 дің көмегімен:
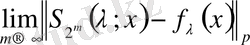
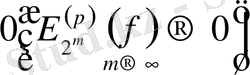
Сонымен қатар
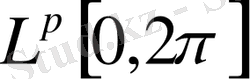 жағдайда
жағдайда
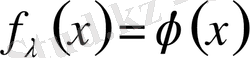 және
және
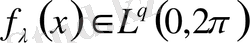
Минковский теңсіздігінен
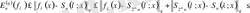
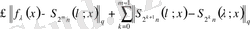
Егер
 онда
онда
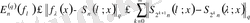 (7)
(7)
(6) -теңсіздіктен (4) -бағалау шығады.
Сонымен келесі теңсіздік орындалады:
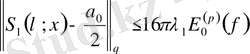
(7) -бағалау бойынша
 (4) -өрнек үшін
(4) -өрнек үшін
 екені шығады.
екені шығады.
Сонымен дәлелдеу аяқталды.
Теорема 2.
Айталық
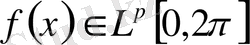
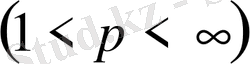 және
және
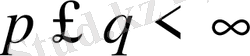 нақты сан болсын.
нақты сан болсын.
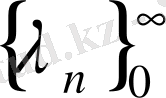 -оң монотонды кемімейтін сан.
-оң монотонды кемімейтін сан.
Егер
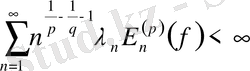
болса, онда мына қатар
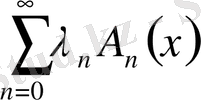
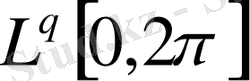 класында жатқан
класында жатқан
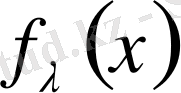 функциясының Фурье қатары және
функциясының Фурье қатары және
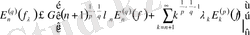
мұндағы
 -абсолютті тұрақты.
-абсолютті тұрақты.
Егер
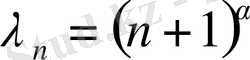
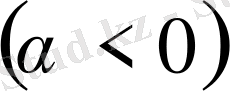 және
және
 немесе
немесе
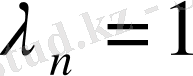 болса, бұдан Конюшков теоремасы келіп шығады.
болса, бұдан Конюшков теоремасы келіп шығады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz