Кеңістіктік бағытқа ғарышнамалық үдету параметрінің тәуелділігі

Пән: Астрономия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

жұмыста көңіл солтүстік және оңтүстік жұлдыз аспаны үшін Хаббл диаграммасының асимметриясына аударылды. Бұл асимметрия, авторлардың сөзі бойынша, жұлдыздардың пекуляр қозғалыстарымен түсіндіріле алмайды, тек ғана ғаламдық координаттармен бөлінген бағыттың бар болуымен 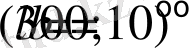. Бұл бағыт ескерілетін жұмыста анықталды R. -G. Cai and Z. -L. Tuo [26] . Онда ғаламдық координаттары анығырақ анықталатыны көрсетілген, нақтырақ (l, b) = 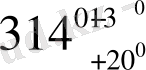, , 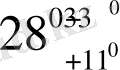а Әлемнің жылдамдауы

[24] жұмысты тағы алыстаған ғаламдарға қатысты Күннің пекуляр жылдамдығы шаманың қызыл ығысуы бойынша ~ 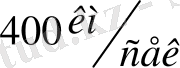бағытта 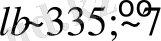. батқыл бағаланғандығын байқаймыз. Ол Әлем осінің бағытымен біздің есептеулерімізбен жаман келісілмейді - . Келесі өлшеулерде [27] күн жүйесі ғаламдық бойлықтың бағытына қозғалатынын көрсетті 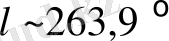және ғаламдық кеңдіктің 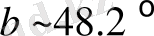, реликтивті сәулеленудің диполды поляризациясы тударады. Бұндай ғаламдық координаттар, [28] сәйкес, біздің шамаларымызға сәйкес [24] жұмыс болжамдарына жақынырақ.

анизотропия параметрінің максималды мәні бар .

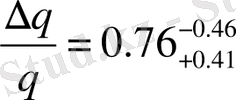Осы байланыстан сұрақ туындайды, Әлемнің осінен бөлінгендер қандай физикалық себептермен туындауы мүмкін? Оған жауап беру үшін негізгі ғаламдық теңдеулерді қарастырамыз.

Әлемнің біртекті изотропты үлгісі үшін жазық кеңістіктік бөлімнің ( 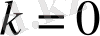) стандартты түрде метрикасы бар

. (29)

Сондықтан Эйнштейн талдауы ғаламдық фактор үшін 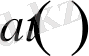келесі түрде жазылады

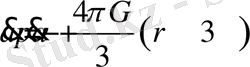, (30)

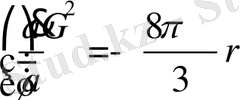, (31)

. (32)

Белгілі болғандай, бұндай теңдеулер ньютондық механика шеңберінде шығаруға болады. Радиустың сферлық-симметриялық денесін қарастырамыз 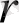, зат тығыздығымен шоғырландырылған 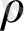, ал оның жылдамдығының таралуы Хаббл заңына бағынады

. (33)

Сфера жоғары жағында орналасқан сынақ бөлшектің қозғалыс теңдеуі санаудың қозғалмайтын жүйесінде мынадай түрде

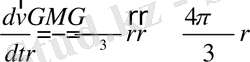. (34)

Шындығында, Толман түрленуін жүргізе отырып сәйкесінде [30], 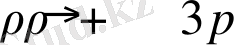, қозғалыс теңдеуіне қысымның әсерән есепткуге мүмкіндік беретін, және оны қоя отырып (34), теңдеуін аламыз (30) . Екі бөлімді жылдамдыққа көбейте отырып (34) 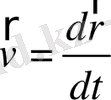, (30) заңмен байланысты (32) сақталған (31) теңдеуін аламыз.

Біздің мақсатқа жету үшін, қашықтық келесі түрде өрнектеледі

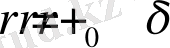, (35)

бұнда 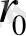біртекті кеңістікте арақашықтық, а - Әлемнің мүмкін анизотропиясын сипаттайтын кіші қосымша мүше. (35) ті (34) қоя отырып теңдеуін аламыз

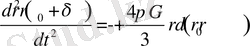, (36)

Екі бөлімге бөлінуі мүмкін: негізінен

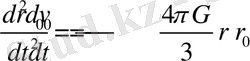(37)

және ауытқыған

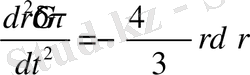. (38)

Ары қарай бір біріне тәуелсіз теңдеулер сияқты қарастырамыз. Жоғарыда ескерілген Толман түрленуін жүргізе отырып 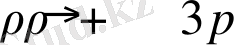, және оларды (37) қойып, келесі теңдеуді аламыз

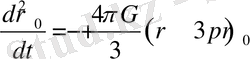. (39)

Ғарыш вакуумы жағдай үшін ( 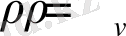, 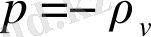) из (39) Әдем дамуының инфляциялық режимін аламыз

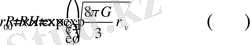. (40)

Осы жерден Хаббл кеңею заңы байқалады

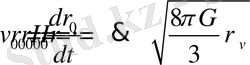(41)

Және оныі жылдамдауына сәйкес

. (42)

Енді (38) теңдеуін қарстырамыз, жобалай отырып, онда 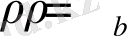, бұнда 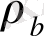- барионды заттың тығыздығы. Бұл тозаң яғни қысым онда нолге тең екендігін есептер қарапайымдылығ үшін бірге қабылдаймыз.

Сөйтіп, біз ғарыш вакуумы мен тозаңнан тұратын, міндеттер жағдайы бойынша бір бірімен араларында өзара әрекет етпейтін Әлемнің екікомпонентті үлгісін қарастырамызй.

Мәнді енгізе отырып 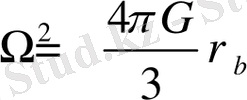, (38) түріне түрлендіреміз

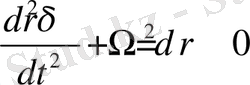. (43)

Бұл тербелмелі теңдеудің үш түбірі бар

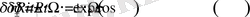. (44)

Олар екі ауықуға әкеледі ((41) қатынасы бойынша) жылдамдықтарды

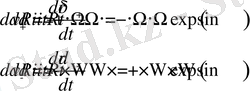(45)

Және жылдамдатуда екі ауытқуға

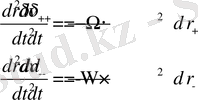. (46)

Физикалыө көзқарас бойынша (45) және (46) өрнек барионды (шаң тәрізді) құрамның ғарыш вакуумында әртүрлі жылдамдықтар мен үдетуде қарама қарсы бағытта ағатын екі кеңістіктік ағымды тудырады. Сөйтіп, кейбір сынақ денелер (ғаламдар) толық жағдай, жылдамдығы және үдетуі үшін келесі өрнектерді жазуға болады

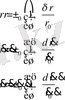(47)

Сондықтан ғаламдық үдету параметрі дәлдәкпен жоғары емес 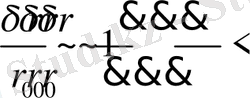түрде

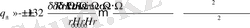. (48)

Анықтамасын пайдалана отырып и , жаңа коэффициент енгіземіз 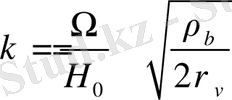. Сыни тығыздық бірліктерде болғандықтан 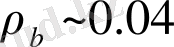, ал вакуум тығыздығы 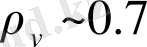, онда коэффициент .

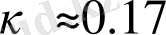(48) өрнектен Хабблдың вакуум ағымына қатынасы бойынша екі барионды ағымдар арасында үдеудің салыстырмалы айырмашылығын табуға болады -

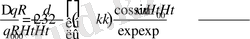. (49)

Қазіргі кезең үшін 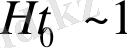, жақындата аламыз 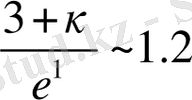. Сондықтан оң жақтағы бірінші қосылу (49) 1. 2 жетеді, екінші тогда как второе слагаемое стремится к нулю. Итак,

. (50)

3. 1 Жалпы Папапетру теңдігінің Ньютондық жуықтаудағы түрі

Қатысты тензор спинінің ұғымы

Және қатысты масса

$\widetilde{\rho} = \sqrt{- g}\rho\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)$

Энергияның сақталу заңына сүйене келіп, келесі теңдеуді аламыз

$\nabla_{v}T^{\mu v} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3)$

$\int_{\sigma}^{\ }{\frac{D}{ds}\left( \widetilde{\rho}u^{\alpha} + u_{\beta}\frac{D{\widetilde{S}}^{\alpha\beta}}{ds} \right) d\sigma} = - \frac{1}{2}\int_{\sigma}^{\ }{u^{\lambda}R_{\mu\nu\lambda}^{\alpha}{\widetilde{S}}^{\mu\nu}d\sigma}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)$

$\int_{\sigma}^{\ }{\frac{D{\widetilde{S}}^{\alpha\beta}}{ds}d\sigma} + \int_{\sigma}^{\ }{u_{\gamma}\left( u^{\alpha}\frac{D{\widetilde{S}}^{\beta\gamma}}{ds} - u^{\beta}\frac{D{\widetilde{S}}^{\alpha\gamma}}{ds} \right) d\sigma} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5)$

Бұл формулалар Папапетру теңдігінің интегралды функциясы, шекті көлемдегі гравитациялық өрістегі жылдамдықты сипаттайды. Келесіде ньютондық жақындауды және шамаларды . . . денелердің өлшемімен және d арақашықтықтарды қарастырамыз.

Яғни ньютондық таралу (5) сияқты орын алады да,

$\underset{1}{\overset{\frac{d}{dx^{0}}}{︸}}\int_{\sigma}^{\ }\underset{3 + 5}{\overset{{\widehat{S}}^{kl}}{︸}}d\sigma = \underset{4}{\overset{Q^{kl}}{︸}} + \underset{6}{\overset{Q^{kl}}{︸}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6)$

$\underset{4}{\overset{Q^{kl}}{︸}} = \int_{\sigma}^{\ }{\left\{ \frac{1}{2}\left( \underset{2}{\overset{g_{00, k}}{︸}}\underset{4}{\overset{{\widehat{S}}^{0l}}{︸}} + \underset{2}{\overset{g_{00, l}}{︸}}\underset{4}{\overset{{\widehat{S}}^{0k}}{︸}} \right) + \frac{1}{2}\left\lbrack \left( \underset{3}{\overset{g_{m0, k}}{︸}} - \underset{2 + 1}{\overset{g_{mk, 0}}{︸}} - \underset{3}{\overset{g_{k0, m}}{︸}} \right) \underset{3}{\overset{{\widetilde{S}}^{lm}}{︸}} - \left( \underset{3}{\overset{g_{m0, l}}{︸}} - \underset{2 + 1}{\overset{g_{ml, 0}}{︸}} - \underset{3}{\overset{g_{l0, m}}{︸}} \right) \underset{3}{\overset{{\widetilde{S}}^{km}}{︸}} \right\rbrack + \underset{2}{\overset{g_{00, m}}{︸}}\left( \underset{3}{\overset{{\widetilde{S}}^{km}}{︸}} \bullet \underset{1}{\overset{v^{l}}{︸}} - \underset{3}{\overset{{\widetilde{S}}^{lm}}{︸}} \bullet \underset{1}{\overset{v^{k}}{︸}} \right) + \frac{1}{2}\underset{1}{\overset{v^{n}}{︸}} \right\} d\sigma, \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) }$

Мұнда ньютондық бұрыштық момент нолге тең( Q=0), ал релятивистік момент

$\frac{1}{2}\left( \underset{2}{\overset{g_{00, k}}{︸}}\underset{4}{\overset{{\widehat{S}}^{0l}}{︸}} + \underset{2}{\overset{g_{00, l}}{︸}}\underset{4}{\overset{{\widehat{S}}^{0k}}{︸}} \right) + \frac{1}{2}\left\lbrack \left( \underset{3}{\overset{g_{m0, k}}{︸}} - \underset{2 + 1}{\overset{g_{mk, 0}}{︸}} - \underset{3}{\overset{g_{k0, m}}{︸}} \right) \underset{3}{\overset{{\widetilde{S}}^{lm}}{︸}} - \left( \underset{3}{\overset{g_{m0, l}}{︸}} - \underset{2 + 1}{\overset{g_{ml, 0}}{︸}} - \underset{3}{\overset{g_{l0, m}}{︸}} \right) \underset{3}{\overset{{\widetilde{S}}^{km}}{︸}} \right\rbrack + \underset{2}{\overset{g_{00, m}}{︸}}\left( \underset{3}{\overset{{\widetilde{S}}^{km}}{︸}} \bullet \underset{1}{\overset{v^{l}}{︸}} - \underset{3}{\overset{{\widetilde{S}}^{lm}}{︸}} \bullet \underset{1}{\overset{v^{k}}{︸}} \right) + \frac{1}{2}\underset{1}{\overset{v^{n}}{︸}}\left\lbrack \left( \underset{2}{\overset{g_{mn, k}}{︸}} - \underset{2}{\overset{g_{mk, n}}{︸}} - \underset{2}{\overset{g_{nk, m}}{︸}} \right) \underset{3}{\overset{{\widetilde{S}}^{ml}}{︸}} - \left( \underset{2}{\overset{g_{mn, l}}{︸}} - \underset{2}{\overset{g_{ml, n}}{︸}} - \underset{2}{\overset{g_{nl, m}}{︸}} \right) \underset{3}{\overset{{\widetilde{S}}^{mk}}{︸}} \right\rbrack + \left( \underset{4 + 1}{\overset{\frac{d{\widetilde{S}}^{0k}}{dx^{0}}}{︸}} \bullet \underset{1}{\overset{v^{l}}{︸}} - \underset{4 + 1}{\overset{\frac{d{\widetilde{S}}^{0l}}{dx^{0}}}{︸}} \bullet \underset{1}{\overset{v^{k}}{︸}} \right)$

Ньютондық теңдеудің жылдамдығы

$\underset{1}{\overset{\frac{d}{dx^{0}}}{︸}}\int_{\sigma}^{\ }\underset{2 + 1}{\overset{\rho \bullet v^{k}}{︸}}d\sigma = - \frac{1}{2}\int_{\sigma}^{\ }{\underset{2 + 2}{\overset{\rho \bullet g_{00, k}}{︸}}d\sigma}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8)$