Квадраттық үшмүшеліктер мен квадраттық теңдеулер: түбірлер, дискриминант, жіктеу және Виет теоремесі


квадраттық үшмүшелік
Көпмүшеліктің түбірі.
Бір айнымалысы бар
Р(х) =а
0
х
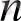 +a
+a
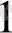 Equation. 3 х+ . . . +а
п
Equation. 3 х+ . . . +а
п
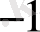 х+а
х+а
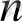 көпмүшелігін қарастырайық.
көпмүшелігін қарастырайық.
А н ы қ т а м а. Қөпмүшеліктің мәнін нольге айналдыратындай айнымалының мәні көпмүшеліктің түбір деп аталады.
Мысалы, х=1 - х 4 -Зх 2 + 4х-2 көпмүшелігінің түбірі болады.
Бір айнымалысы бар екінші дәрежелі
ах
 +bх+с (а
+bх+с (а
 0)
көпмүшелігін қарастырайық. Бұл өрнекті
квадраттық үшмүшелік
деп те атайды. Осы квадраттық үшмүшеліктің түбірлері
ах
2
+bх+с=0 (а
0)
көпмүшелігін қарастырайық. Бұл өрнекті
квадраттық үшмүшелік
деп те атайды. Осы квадраттық үшмүшеліктің түбірлері
ах
2
+bх+с=0 (а
 0)
квадраттық теңдеуінің шешімдері болады (теңдеудің шешімдері жоқ болса, квадраттық ушмүшеліктің түбірлері де жоқ болады) .
0)
квадраттық теңдеуінің шешімдері болады (теңдеудің шешімдері жоқ болса, квадраттық ушмүшеліктің түбірлері де жоқ болады) .
Мысал. Зх 2 +5х-2 квадраттық ушмүшелігінің тубірлерін табу керек.
Шешуі. Зх 2 + 5х-2 = 0 теңдеуін шешейік.
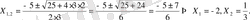
Олай болса, -2 мен 1/3 сандары Зх 2 + 5х-2 квадраттық үшмүшелігінің түбірлері болады.
Квадраттық үшмүшелікті кeбейткіштерге жіктеу
.
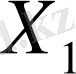 мен
мен
х
2
ах
2
+bх+с (a
 0)
квадраттық үшмүшелігінің түбірлері болсын. Бұл жағдайда квадраттық үшмүшелікті көбейтінді түрінде
ах
2
+bх+с=а(
0)
квадраттық үшмүшелігінің түбірлері болсын. Бұл жағдайда квадраттық үшмүшелікті көбейтінді түрінде
ах
2
+bх+с=а(
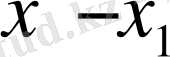 )
(х-
х
2
) деп өрнектеуге болатынын көрсетейік. Осы тепе-теңдікті дәлелдеу үшін оның оң жағын түрлендірейік:
)
(х-
х
2
) деп өрнектеуге болатынын көрсетейік. Осы тепе-теңдікті дәлелдеу үшін оның оң жағын түрлендірейік:
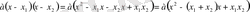
Ал
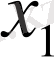 мен х
2
ах
2
+bх+с = 0 квадраттық теңдеуінің шешімдері, сонда
мен х
2
ах
2
+bх+с = 0 квадраттық теңдеуінің шешімдері, сонда
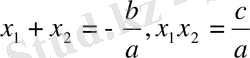 теңдіктері орындалады. Бұл ауыстыруларды іске асырып,
теңдіктері орындалады. Бұл ауыстыруларды іске асырып,
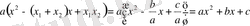 екенін аламыз. Тепе-теңдік дәлелденді.
екенін аламыз. Тепе-теңдік дәлелденді.
Мысалдар. 1. 5х 2 -4х-12 квадраттық үшмүшелігін көбейткіштерге жіктеу керек.
Ол үшін квадраттық үшмүшеліктің түбірлері, яғни 5х 2 -4х-12 = 0 теңдеуінің шешімдерін табу керек:
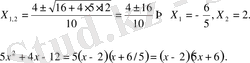
2.
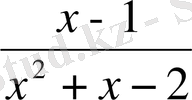 бөлшегін қысқарту керек.
бөлшегін қысқарту керек.
Шешуі х 2 + х-2 квадраттық үшмүшелігін көбейткіштерге жіктейік:
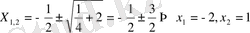
Демек, х 2 +х-2= (х-1) (х+2) . Олай болса,
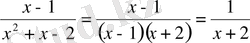
Квадраттық теңдеулерді шешу . Анықтама. Квадраттық теңдеу деп
ах 2 + bх+с = 0 (1)
түріндегі теңдеу аталады. Егер b=0 немесе с = 0 болса, онда квадратгық теңдеу толық емес теңдеу деп аталады.
Толық емес квадраттық теңдеулерді қарастырайық.
а) b=0 болсын, сонда
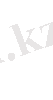
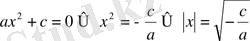 .
.
Сонымен, ах
2
+с =0 теңдеуі
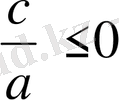 болғанда екі шешімге ие
болғанда екі шешімге ие
болады.
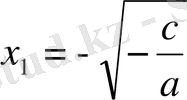 ;
;
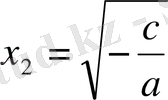 ( с=0 болғанда
( с=0 болғанда
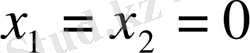 , яғни -0=+0=0)
, яғни -0=+0=0)
Мысал. х 2 - 4 = 0 теңдеуін шешейік.
Шешуі.
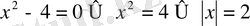 . Теңдеудің екі шешімі бар:
. Теңдеудің екі шешімі бар:
 және х
2
= 2.
және х
2
= 2.
б) с = 0,
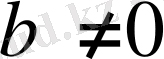 болсын. Сонда квадраттық теңдеу ах
2
+ bх = 0. түрінде болады. х-ті жақша сыртына шығарсақ,
х(ах + b)
=0. болады. Көбейтінді нольге тең болуы үшін көбейткіштердің кем дегенде біреуі нольге тең болуы керек:
болсын. Сонда квадраттық теңдеу ах
2
+ bх = 0. түрінде болады. х-ті жақша сыртына шығарсақ,
х(ах + b)
=0. болады. Көбейтінді нольге тең болуы үшін көбейткіштердің кем дегенде біреуі нольге тең болуы керек:
 және
және
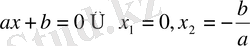 Сонымен, бұл жағдайда екі шешім алдық: х=0,
х
2
=
Сонымен, бұл жағдайда екі шешім алдық: х=0,
х
2
=
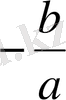
Мыса л. 4х 2 -х=0 теңдеуін шешу керек.
Шешуі. 4х
2
-х=0
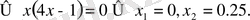
Енді толық қвадраттық теңдеуді
ах
2
+bх+с=0 (
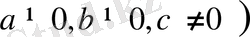 қарастырайық та оның түбірлері формуласын қорытайық. Теңдеудің сол жақ бөлігін, одан толық квадратты ажырату арқылы түрлендірейік:
қарастырайық та оның түбірлері формуласын қорытайық. Теңдеудің сол жақ бөлігін, одан толық квадратты ажырату арқылы түрлендірейік:
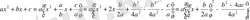
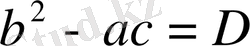 деп белгілtйік. Сонда үш жағдай болуы мүмкін.
деп белгілtйік. Сонда үш жағдай болуы мүмкін.
1) Егер
D=0
болса, онда
ах
2
+bх+c
=
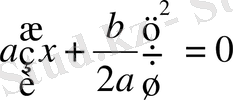 болады да, теңдеудің бір ғана шешімі бар:
болады да, теңдеудің бір ғана шешімі бар:
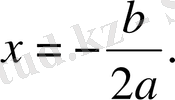
2) Егер
 <0 болса, онда
<0 болса, онда
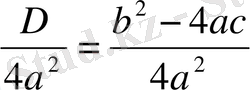 бөлшегі теріс таңбалы болады да
бөлшегі теріс таңбалы болады да
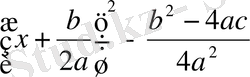 Equation. 3 өрнегі х-тің кез келген мәнінде оң таңбалы болады. Бұл жағдайда (I) теңдеудің нақты мәнді шешімдері жоқ.
Equation. 3 өрнегі х-тің кез келген мәнінде оң таңбалы болады. Бұл жағдайда (I) теңдеудің нақты мәнді шешімдері жоқ.
3) Енді D>0 болсын. Сонда (1) тендеу
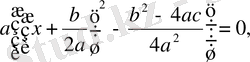 D Equation. 3
D Equation. 3
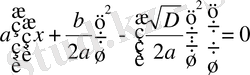 теңдеуіне пара-пар. Квадраттардың айырымын көбейткіштерге жіктей отырып,
теңдеуіне пара-пар. Квадраттардың айырымын көбейткіштерге жіктей отырып,
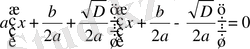
теңдеуін аламыз
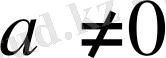 болғандықтан
болғандықтан
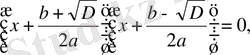
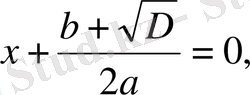
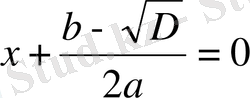 .
.
теңдеулері шыгады. Бұрдан
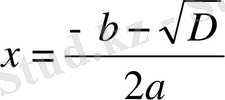 не
не
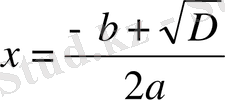 .
.
Олай болса, бұл жағдайда квадраттық теңдеудің екі шешімі бар болады, оларды былай қысқаша жазу қабылданған:
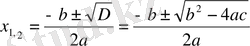
 өрнегі квадраттық теңдеудің дискриминанты деп аталады. Сонымен дискриминанттың таңбасына байланысты квадраттық теңдеуді шешкенде үш жағдай кездеседі.
өрнегі квадраттық теңдеудің дискриминанты деп аталады. Сонымен дискриминанттың таңбасына байланысты квадраттық теңдеуді шешкенде үш жағдай кездеседі.
Егер D>0 болса, онда квадраттық теңдеудің екі шешімі бар болады.
Егер D=0 болса, онда квадраттық теңдеудің бір ғана шешімі бар болады.
Егер D<0 болса, онда квадраттық теңдеудің нақты мәнді шешімдері болмайды.
Мысал.
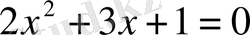 теңдеуін шешейік. (а=0, b=3, c=1)
теңдеуін шешейік. (а=0, b=3, c=1)
Шешуі. Теңдеудің дискриминантын құрамыз.
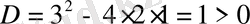 . Сонда
. Сонда
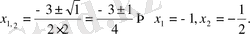
Анықтама.
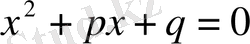 (2) түріндегі теңдеу келтірілген квадраттық теңдеу деп аталады. Толық квадраттық теңдеуді оның оң жағын да, сол жағын да а-ға бөліп, (2) теңдеу түріне келтіруге болады:
(2) түріндегі теңдеу келтірілген квадраттық теңдеу деп аталады. Толық квадраттық теңдеуді оның оң жағын да, сол жағын да а-ға бөліп, (2) теңдеу түріне келтіруге болады:
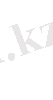
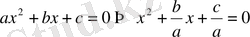 .
.
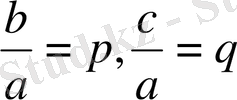 деп белгілеп, келтірілген квадраттық теңдеуді аламыз:
деп белгілеп, келтірілген квадраттық теңдеуді аламыз:
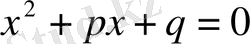 Келтірілген квадраттық теңдеудің шешімдері формуласын жазайық :
Келтірілген квадраттық теңдеудің шешімдері формуласын жазайық :
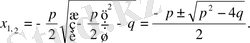
Мысал.
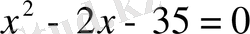 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі. p=2, q=-35 болғандықтан, формула бойынша
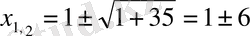 және
және
 ,
,
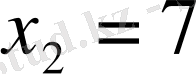
Виет теоремасы.
ах
2
+ bх+с =
0 (
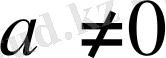 ) квадраттық теңдеуінің (
) квадраттық теңдеуінің (
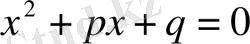 теңдеуінің де)
теңдеуінің де)
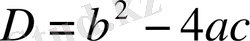 >0 (
>0 (
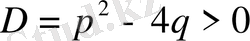 ) , болғанда екі шешімі бар.
) , болғанда екі шешімі бар.
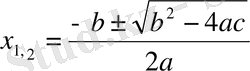 ,
,
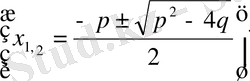 енді осы шешімдердің қосындысы мен көбейтіндісін анықтайық:
енді осы шешімдердің қосындысы мен көбейтіндісін анықтайық:
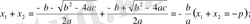
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz